Pattern Recognition for Flank Eruption Forecasting: An Application at Mount Etna Volcano (Sicily, Italy) ()
Received 24 November 2015; accepted 23 July 2016; published 26 July 2016

1. Introduction
Mt. Etna, located on the east coast of Sicily (Figure 1), is Europe’s largest and most active volcano as well as one of the best-monitored volcanoes worldwide. Every few years, eruptions occur from flank fissures concentrated mainly along the NE and S rift zones on the slopes of the volcano (Figure 1). These events have critical socioeconomic consequences, especially due to lava flows that threaten the densely urbanized area surrounding the city of Catania (almost one million people) and major infrastructures (e.g. international airport, railway and skiing stations). The knowledge and subsequent awareness of the volcanic risk are therefore fundamental for decision-makers who are called on to manage appropriate emergency procedures.
The wide spectrum of styles and intensities of volcanic phenomena observed at Mt. Etna (degassing, Strombolian activity, lava fountains with ash fallout, phreatic and flank eruptions), coupled with the multidisciplinary data collected at Istituto Nazionale di Geofisica e Vulcanologia-Osservatorio Etneo (hereafter, INGV-OE), give an unique opportunity to better understand and/or distinguish between pre-eruptive phases. Accordingly, implementing a great variety of innovative models based on the Artificial Sciences is proposed. Artificial Sciences (hereafter, AS) enable comprehending natural processes by reproducing those same processes by automatic models.
A volcano is identifiable as a complex system, a spatio-temporal region, in which the structure and the state of its components change due to the dynamics linked to local and/or regional interactions (e.g. tectonic stresses), while maintaining its space-time cohesion. Being a dynamic system, a volcano generates new information over time, both in long, medium and short term (for Mt. Etna, years, months/weeks and weeks/days, respectively). Consequently, a volcano is inferred as a natural Adaptive System.
In a complex system, the global behavior does not equal the sum of the state of its components. This means that a complex system presents a highly nonlinear behavior, with a multiphase energy landscape; its dynamics is therefore not graspable by equations in a closed form [1] . To understand the actual dynamics of a natural Adaptive System, we need a specific mathematics working directly on data in a way that the global behavior of the system occurs spontaneously by the local interactions of its components, i.e. data and equations. This is the basis of the Bottom-Up method (Natural Computation), representing the best way for the study of natural Adaptive System [2] .
The mathematical expression of the Natural Computation method is represented by the so-called Artificial Adaptive Systems. In natural systems there is hidden information that makes the data noticeable and easily measureable. The hidden information reveals the underlying model that the natural Adaptive System is going to pursue. Artificial Adaptive Systems work by seeking for traces of this hidden information [1] .
The main goal of this article is a Pattern Recognition; in other words, we have tried to understand if an eruption can be recognized, using only the distributed geo-information detected every day by local sensors.
We have worked applying the following steps:
1) A data preparation task in order to make the numerical information embedded in the original data explicit; we then created a data matrix (i.e. a data set), where each row (record) represents what the sensors detect every day and each column represents a different attribute (sensor measure) of each day;
2) We assigned a target to each record (i.e. day monitored): if, according to our previous knowledge, an eruption would occur or not on each day;
3) We used the special adaptive Training With Input Selection and Testing algorithm (hereafter, TWIST) to select the minimum attributes able to maximize the pattern recognition task;
4) We applied a 5 × 2 Cross Validation (hereafter, CV) protocol to split the restricted data set (with a selected number of attributes) to establish the sensitivity and specificity of our pattern recognition algorithms;
5) Finally, we compared different classification algorithms (Artificial Neural Networks (hereafter, ANNs) and Machines Learning (hereafter, MLs)), to understand if this pattern recognition task may have suitable results and
![]()
Figure 1. Sketch map of Mt. Etna volcano. Triangles indicate sensor locations. Different colors refer to different monitoring: green, yellow, blue and red stand for geochemical emissions, ground deformation, gravity and tilt measurements, respectively. Acronyms as listed in Table 2.
which algorithm performs best.
Sensitivity and specificity are estimated as follows:
 (1)
(1)
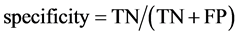 (2)
(2)
where TP, TN, FP and FN stand for True Positive, True Negative, False Positive and False Negative, respectively.
Furthermore, this paper presents a pattern recognition task, which is not necessarily a predictive task. Given a specific distribution of signals, the ML is able to estimate if this distribution is a typical distribution of an incoming eruption process.
2. Data
A source dataset represents most of the knowledge we have of the assigned target. Thus, we need to generate two equivalent subsets of data from a statistical point of view. Therefore, if this is true, the training session will represent a suitable learning set for the ML and the outputs of testing session will be representative of the ML capability to generalize for the whole dataset.
The dataset analyzed here deals with monitoring parameters recorded and collected at Mt. Etna in the interval January 2001-April 2005 (a total of 1581 days). This choice was motivated by the fact that the selected interval comprised various activity stages of Mt. Etna, ranging from quiescence to Strombolian activity, lava fountains and lava flank emissions. In particular, due to the target (i.e. the prediction of flank activity), we focus our attention on the flank eruptions occurring in 2001 (July 17-August 9, for a total of 24 days), 2002-2003 (October 27- January 28, for a total of 94 days) and 2004-2005 (September 7-March 8, for a total of 183 days), for an overall of 301 eruptive days [3] .
The dataset contains hidden information of the physical processes occurring inside the conduit of a volcano during or immediately preceding an eruption. These subsurface processes are related to data collected during volcano monitoring [4] . At Mt. Etna, seismicity(both high frequency and long period events), ground deformations (tilt, EDM distances, areal dilatation, slip-rate), volatile degassing (SO2 and CO2 flux emissions, molar SO2/HCl, SO2/HCF and HCl/HF ratios, and isotopic 3He/4He ratio), potential fields (both gravimetric and magnetic), volcanic and geological data (ash emission and dry fractures) are monitored and collected daily. Other data are retrieved by laboratory observations, such as petrologic analysis of the volcanic rocks produced by volcanism (e.g. the presence of sideromelane in volcanic ash is indicative of a fresh magma injection).
The present dataset is a revision of a collection used to estimate the probabilities of eruptions, and relative pre-eruptive phases (unrest and nature of the unrest), by applying a Bayesian Event Tree procedure [3] .
The revision works on those parameters whose time series are replicated indifferent nodes only because of different thresholds of anomaly [3] . A further revision is needed for parameters whose time series is shorter than 1581 days (i.e. tremor data). Therefore, from the initial dataset of 39 monitoring parameters [3] , we elaborate only 28 parameters (Table 1), to which are associated two classes (Eruption and NonEruption) and 1581 records. In the present analysis, a monitoring parameter is assumed as a variable and no distinction among nodes is made.
A brief description of the parameters follows. The entire dataset is listed in Table 1, and a relative shortening for software applications is given in Table 2. Clearly, the whole network deployed on the Mt. Etna edifice is suitable to monitor internal volcanic processes. Indeed, parameters collected in specific zones (Table 1) are better related to the different regimes of volcanic activity, starting from an unrest state, even though on different timescales (it is worth recalling that our aim is predicting flank activity).
The deep (>200 km) and energetic (M > 5.0) earthquakes occurring on the Tyrrhenian slab as well as seismicity located in specific sectors (W and NW) are associated to the innermost magma movements [3] . Conversely, intense shallow VT seismicity (<5 km) is in line with shallower intrusions, most often being a precursor of flank eruptions at Mt. Etna, at least on a timescale of a few days ( [3] and reference therein).
Ground deformation data are commonly linked to inflations of the volcanic edifice, on a timescale of months; relative uplifts increase until the magma is erupted ( [3] and reference therein). Conversely, tilt data show significant variations on a shorter timescale of a few hours to days [Gambino, personal communication]. Furthermore, GPS data, mostly collected on SE flank (Figure 1), are significant to detect anomalies for deep intrusions, while tilt data are better associated to shallow intrusions (Figure 1; [3] and reference therein).
Gravity data are related to magma intrusive processes, on a timescale of weeks to months ( [3] and reference therein). Data convey a local effect, that is higher anomalies are detected at stations located closer to magmatic mass movements. Locations of the benchmarks used in this study are shown in Figure 1.
The geochemical fluids considered here are the emissions of SO2 and CO2 from the summit crater and the soil,
![]()
Table 1. Setting monitoring component for the analyzed 2001-2005 period at Mt. Etna. Relative units are shown.
respectively. In particular, CO2 data are collected from stations located on SW and E flanks (i.e. P39 and P78, respectively; Figure 1). Both sites are characterized by the highest gas concentration in the soil, being connected to deep magma source and shallower reservoir, respectively. Both parameters are linked to the internal volcanic processes onetime scale of weeks to months ( [3] and reference therein). In particular, increases in the soil CO2 fluxes are normally followed by marked decreases when the magma rises to the surface in the days preceding the eruptions, or accompanies intrusions to shallower levels [3] .
For the petrological data, the sideromelane parameter indicates material derived directly from the magma that reached the surface [4] .
Some details of the structure of the present dataset are due. Monitoring temporal series were collected daily, even though dealing with discrete sampling, such as seismological data (counts of earthquake), ash emission, and tilt data. Gas emissions were collected during occasional campaigns and, therefore, relative time series have sparse missing data. For analysis purposes, those missing data are retrieved by a linear interpolation. On the contrary, gravity data at FM4 and PL benchmarks (belonging to the E-W and N-S profiles, respectively), as well
![]()
Table 2. Original variables (28) of the analyzed dataset vs the Input Selection (11) executed by TWIST algorithm (in italics and bold). Linear correlation of each attribute with the desired target (i.e. Eruption) is also reported.
aShortening for software purposes; b(Pearson) linear coefficient.
other geodetic data than tilt, report daily rates for missing data. It has to be stressed that input data are normalized as required to avoid overweighting certain components just for their physical dimensions.
Figure 2 shows an inventory (crater SO2 emissions and gravity measurements) of the monitoring dataset here analyzed. It is evident how the data show changing with time and how they are related to different volcanic scenarios, switching from quiescence to flank eruptive phases.
3. Methods
3.1. TWIST Algorithm
TWIST is a new evolutionary algorithm [5] able to generate two subsets of data with a very similar probability
![]()
Figure 2. Daily crater SO2 emission (a), gravity at FM4 station (E-W profile) (b) and gravity at PL station (N-S profile) (c) time series (interpolated data). The grey rectangular boxes comprise the time interval of the July-August 2001, October 2002-January 2003, and September 2004-March 2005 flank eruptions, respectively.
density of distribution and with the minimal number of effective variables for pattern recognition.
Consequently, in the TWIST algorithm every individual of the genetic population will be defined by two vectors of different lengths: 1) the first one, showing which records (N) must be stored into the subset A and which ones should be stored into the subset B; 2) the second one, showing which inputs (M) must be used into the two subsets and which ones have to be deleted. Figure 3 illustrates the dynamic of the TWIST algorithm.
The cost function of TWIST for each genetic individual is the lowest fitness of two MLs (kNN, Naïve Bayes, Back Prop or Learning Vector Quantization), each trained on one subsample and tested on the other one.
We have shown in many previous papers [6] - [19] that the TWIST algorithm outperforms the other splitting strategy (i.e. random distribution and K-Fold Cross Validation) in terms of results when they are applied to real medical data and also to classic datasets available from the UCI Machine Learning Repository [20] .
The “reverse strategy” used in this algorithm tends to generate two subsets with the same probability density function, and this is exactly the gold standard of every random distribution criterion [7] . In addition, when the “reverse strategy” is applied, two fitness indicators are generated: the accuracy on the subset B after the training on the subset A, and the accuracy on the subset A after the training on the subset B, being accuracy defined as
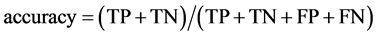 (3)
(3)
where TP, TN, FP and FN are the same as in Equations (1) and (2).
Only the lower accuracy of the two is saved as the best fitness of each individual of the genetic population rather than an average of the two or the higher of the two. This criterion increases the statistical probability that the two sub-samples are equally balanced during the genetic evolution because of the quasi-logarithmic increase of the optimization process. We have also demonstrated experimentally [6] that when there is no information in a dataset, the behaviors of the TWIST algorithm, the Training and Testing Random Splitting and the K-Fold Cross Validation are equivalent. Therefore, TWIST does not code noise to reach optimistic results [6] .
Previous results have shown that the TWIST algorithm is superior to current methods: pairs of subsets with similar probability density functions are generated, without coding noise, according to an optimal strategy that
![]()
Figure 3. Structure of TWIST evolutionary algorithm (modified by [7] ).
extracts the minimal number of features and the most useful information for pattern classification.
After 295 generation TWIST algorithm has selected 11 attributes among the original 28. Table 2 shows the input selection executed by TWIST with the calculation of the linear correlation (hereafter, LC) between each attribute and the target. A possible geostatistical explanation for non-included attributes could be because the sensor produces weak signals, with anomaly variation that may last longer than the typical timescale of a flank eruption at Mt. Etna. Indeed, when an unrest is detected at Mt. Etna (6 - 8 months before the onset of the flank event), if the volcanic system evolves into more anomalous states, mid-term phases occur more frequently and for longer time intervals (few weeks), with a drastic increases very few days or hours before fracturing the volcano slopes [3] . It should also be noted that volcanic signals might be scarcely detected because of the non-op- timal location of the relative sensors.
It is interesting to observe that the TWIST algorithm does not select the attribute with the highest LC with the target. Many variables with a very low LC with the dependent variables are in fact chosen. This is because TWIST operates a many to many non-linear associative work among all the variables, in order to detect also which weak non-linear signals make the other signals become good predictors.
3.2. The 5 × 2 CV Protocol
The validation protocol is a fundamental procedure to verify the ability of models to generalize the results reached in the Testing phase of each model. The application of a fixed protocol measures the level of performance that a model can produce on data that are not present in the Testing and/or Training sample. There are different types of protocol in the literature, each with advantages and disadvantages. The protocol, from the point of view of a general procedure, consists of the following steps:
1) subdividing the database in a random way into two subsamples: Subsets A and B;
2) training an ANN (or a generic algorithm) on Subset A; in this phase the ANN learns to associate the input variables with those that are indicated as targets;
3) at the end of the training phase, the weight matrix produced by the ANN is saved and frozen together with all the other parameters used for the training;
4) with the weight matrix saved, Subset B, which it has not seen before, is shown to the ANN, so that in each case the ANN can express an evaluation based on the previous training; this operation takes place for each input vector and every result (output vector) and is not communicated to the ANN; in this way the ANN is evaluated only in reference to the generalization ability that it has acquired during the Training phase;
5) a new ANN is constructed with identical architecture to the previous one and the procedure is repeated from point 1, but this time the ANN will be trained on Subset B and blindly tested on the Subset A.
This general training plan has been further articulated with the aim of increasing the level of reliability in terms of generalization of the processing models. More specifically, we employed the so-called 5 × 2 Cross Validation protocol [21] . In this procedure the study sample is randomly divided five times into two sub samples, always different but containing a similar distribution of cases and controls: the training one (containing the dependent variable) and the testing one. During the training phase the ANN learns a model of data distribution and then, on the basis of such a model, classifies subjects in the testing set in a blind way. The training and testing sets are then reversed and consequently 10 analyses for every model employed are conducted. The results of this protocol represent a robust statistic for pattern recognition work. Figure 4 shows the 5 × 2 CV protocol and Table 3 shows a five splitting of the dataset in two subsamples.
3.3. ANNs and MLs
We have tested 10 different and known algorithms, coming from five families of MLs [22] :
1) ANNs, advanced and classic:
a) Supervised Contractive Map (SV-Cm) [23] [24] ;
b) Sine Net, trained with 1 hidden layer of 12 units and a Learning Coefficient = 0.1 [25] ;
c) The classic Multi-Layer Perceptron with the Back propagation learning law (MLP-Bp), trained as Sine Net [26] ;
d) K-Contractive Map (K-CM), trained with 3 hidden layers of 12 units each one and a Learning Coefficient = 0.01 [27] ;
2) Decision Trees [28] : Random Forest, initialized with 100 trees [29] ;
3) Instance Learning: kNN with N = 3 and Euclidean distance [30] ;
4) Functions: SVM in SMO implementation, trained with PUK kernel [31] - [33] and Logistic Regression [34] ;
5) Probabilistic Nets:
a) Bayes Net [35] ;
b) Naïve Bayes [36] .
We have used the following academic software to implement all the algorithms: Weka Data Mining Software [37] and Semeion Software [38] [39] . The dataset was composed from 11 attributes (independent variables), after the TWIST algorithm selection, 2 classes (Eruption, No Eruption) and 1581 records (days monitored). Table 4 shows the results after the 5 × 2 CV protocol applications. In fact, arithmetic average measure must be considered more representative than the weighted average, because the two classes of the sample are very unbalanced.
4. Results
The present dataset includes 28 attributes (i.e. parameters), dealing with the volcanic disciplines routinely monitored and collected at Mt. Etna. The data contains the hidden information related to the flank eruption (i.e. our target).
Important results are first achieved from a mathematical and statistical viewpoint. TWIST algorithm has selected only 11 attributes among the original 28, as features able to recognize a pattern of possible eruption (Table 2).
A very complex and robust protocol was applied to validate this pattern recognition task (the 5 × 2 CV). Table 3 shows the 5 pairs of subsets generated by TWIST for the 5 × 2 CV protocol and also how the 5 pairs of subsets are balanced and representative of the entire dataset. Each algorithm is tested in 10 independent tests and the variance of the results for each algorithm was very low (Table 4). In brief, 100 independent tests of blind validation were set up in this work.
We have applied 10 different MLs, classic and advanced, to teach each algorithm how to blindly recognize the typical pattern of an eruption. The results show that advanced ANNs and Decision Trees are very suitable for this target (from 97% to 99% of accuracy; Table 4), while classic statistical algorithms have some difficulties in managing the complexity of the tested dataset (from 71% to 96%; Table 4). In detail, the best ANNs tested in
![]()
Table 3. A five distribution of the dataset in two subsamples, according to the 5 × 2 CV validation protocol. Eruption columns stand for days (301 out of a total of 1581) in which Mt. Etna underwent flank activity in the studied period (January 2001-April 2005; see text for details).
![]()
Table 4. Blind pattern recognition results of the 10 algorithms, after the application of 5 × 2 CV validation protocol. The arithmetic average column (in bold) stands for the average of the accuracy of classification in each class.
aEruption = Sensitivity; bNo Eruption = Specificity; cArithmetic Average; dWeigthted Average; eError = Average Number of Wrong Classification in the 10 training and testing tasks; fVar% = Percentage Variance of the 10 classifications.
this work show sensitivity over 99% and specificity over 98%, as well as low misclassification estimates (Table 4).
The equivalent geophysical and volcano logical viewpoint is also noteworthy. Geochemical parameters prove the most predictive as associated to the target, showing the highest positive and the lowest negative values of LC coefficient (0.4498 and −0.3367 for the SO2 and CO2_P39 data, respectively; Table 2).
Both selected seismological parameters feature slightly negative LC (−0.0173 and −0.0244 for eqs_slab_Tyrr and eqs_NW_Sect, respectively; Table 2). Indeed, as reported in pertinent literature ( [3] and reference therein), the residue parameters of the analyzed dataset feature the most predictive perspective for our target. These results once again highlight that the eruption represented in the data follows a highly non-linear feature.
Conversely, the ground deformation parameters show positive LC (0.3479, 0.1207 and 0.2318 for dil_W, MtSil_Bocche1792 and MNR, respectively; Table 2), thus indicating that a relative increase is linked to higher probabilities of flank eruption occurrences.
Gravity data feature antithetic LC (0.1017 and −0.0966 for grav_FM4 and grav_PL, respectively; Table 2). As stated before, gravity is closely correlated to local magma movements, hence a positive correlation could be associated to a magma restoration (higher probabilities of impending flank eruption), just as a negative correlation to a magma depletion (lower probabilities estimated for the present target).
Finally, the sideromelane parameter also features a negative LC (−0.0876), thus highlighting an antithetic correlation with the present target.
5. Discussion
A pioneer pattern recognition analysis was successfully applied to the eruptive activity of Mt. Etna in early 1990s [40] . The authors characterized the role of the seismicity regional seismicity, mostly located in northern and northeastern Sicily, as important precursors in triggering Mt. Etna flank activity. Albeita longer investigated period (fifteen years of data), the dataset deals with a minimal source of information with respect to that used in this analysis. Indeed, the actual dataset embraces diversified monitoring fields to draw a vast interconnection. As a matter of fact, past and present results confirm that an operative prediction-oriented application of the recognized precursory patterns to feature flank activity at Mt. Etna is tentatively possible.
In recent years, pattern recognition analysis has been applied with the goal of classifying volcanic tremor data recorded at Mt. Etna and its relation to different regimes of volcanic activity [41] [42] and to integrate tremor data with SO2 flux [43] . In this study, for the first time, a pattern recognition task was performed at Mt. Etna by using different techniques, as well as a wide selection of ANNs and a large monitoring dataset. (Supervised) ANNs resolved the classification problems in terms of non-linear regression rather than linear discrimination, thus highlighting that a volcano is a complex system, whose spatio-time evolution is inferred as a natural adaptive system.
The target of the present analysis was to understand how a monitoring dataset of independent attributes could be considered precursory of a flank eruption at Mt. Etna. The groundwork of volcano monitoring is the collection of experimental physical data and their subsequent analysis and correlation with the associated hidden phenomena.
The dataset included multidisciplinary data collected during the January 2001-April 2005 period, during which the July-August 2001, October 2002-January 2003 and September 2004-April 2005 flank eruptions occurred, for a total of 301 eruptive days out of 1581. The present data were a revision of a pioneer usage of the relative values aimed at forecasting volcanic activity ( [28] attributes in Table 1; [3] ).
The interdisciplinary features of the data were not explored among the parameters, each being analyzed towards to the target (i.e. flank eruption at Mt. Etna). With this goal in mind, a preliminary application of the TWIST algorithm [5] selected the most predictive parameters. TWIST divided the original dataset into five pairs of subsets of data with a very similar probability density of distribution (Table 3). The selection worked on the minimal number of effective variables for pattern recognition, after estimating LC values. In this analysis, 11 (out of 28) variables were selected, with both positive and negative LC values (Table 2). Values of the included attributes better reflect the correlation with the locations of the anomalies occurrence, the relative variations being in line with the timescale of a flank eruption at Mt. Etna. It was interesting to observe that among the 11 variables those attributes having a high LC with the eruptions were not selected; this could again outline that the eruption hidden among the data is a highly non-linear process.
The most predictive results were associated with geochemical fluxes, even though with antithetic LC values (0.4498 and −0.3367, for SO2 and CO2_P39, respectively). Results inferred that an impending flank eruption at Mt. Etna was preceded by an increase of SO2 emission, as well a decrease of CO2_P39 degassing. Both SO2 and CO2 emissions have been observed as mid-term (months) precursory of the flank activity at Mt. Etna and associated to changes in the states of the magmatic gases exsolved from the magma at depth [3] . Crater SO2 fluxes showed decreases during inter-eruptive periods, followed by increasing trends until the eruptions [3] . Conversely, decreases in the soil CO2_P39 were observed during magma shallower intrusions in the days preceding flank eruptions [3] .
The other selected attributes showed lower LC values (both positive and negative) with the target. Even though a significant correlation, anomaly variations are associated with weak signals and/or to slow changes (i.e. increases or decreases display in the relative time series).
We have tested different MLs and different types of ANNs on the selected data in 100 experiments (10 independent training and testing phase for each of the 10 algorithms). Most ANNs have proved to understand fairly well the typical patterns of the flank eruptions, while the classic statistical algorithms have shown more frequent errors in the generalization phase (Table 4). In brief, ANNs seem to be suitable tools to capture the complex and highly non-linear dynamics of flank eruptions in volcanoes.
The potential of the used strategy reflected the reliability of the present dataset in terms of particular zones of the volcano to be affected by anomaly occurrences, interpreted as a change of the inner dynamics of the system. It is well known that specific locations of the volcanic edifices will give clues, usually linked to magma recharging from the source zone. Clearly, Mt. Etna shows a similar behavior, and, as a consequence, most of the analyzed attributes dealt with this sort of information (Table 1). In other words, the position of the volcanic phenomena in a spatial distribution draws an area within which the source of those events is contained, if the events belong to the same process.
When a spatial process (in our case, a flank eruption) emerges through local and discrete events (i.e. monitoring data), there simultaneously emerges a strategic area by which those events acquire an intrinsic meaning emerges simultaneously. This is the area from which all of the events of the process minimize the entropy of their mutual distances [44] .
Most of the selected monitoring parameters (10 out 11, exception is sideromelane; Table 2) deal with a specific zone related to the sensor locations or to a wider geographical sector. The timing of the events and their frequencies seem to be embedded in the spatial distribution of the events themselves; in other words, the temporal dynamics of any process seems to be frozen in the morphology of space [1] .
It is intriguing to observe that most of the selected parameters point out to the western and southeastern flank of Mt. Etna. Indeed, the present application reveals other aspects, such as the possibility to detect forerunning signals of flank eruptions. Indeed, for the July-August 2001 flank eruption, a number of vents opened on the South Rift, as similarly happened the first days of the October 2002-January 2003 event.
6. Conclusions
In conclusion, the results highlighted that the analyzed multidisciplinary dataset of real monitoring values proved to be especially useful for pattern recognition at Mt. Etna. In addition, the (supervised) ANNs potential was well exploited in identifying the transitional state between eruptive and non-eruptive phases, which is of outstanding interest for surveillance purposes.
Further refinement of the present dataset can be achieved in terms of missing data. Missing data concerned parameters whose time series were acquired by occasional (GPS and geochemical measurements) or seasonal (gravity measurements) campaigns. Indeed, it is unknown how the volcanic phenomena could evolve if no relative measurements are associated. A more complete time series could deal with a more suitable description of the related inner dynamics, probably diminishing (but not eliminating) the non-linear feature of the complex volcanic system.
This study introduces fundamental concepts regarding monitored volcanic signals and pattern recognition systems, highlighting future directions for research and challenges to bridge the gap in the transfer of prototype academic results to deployed technology.
Acknowledgements
INGV-OE kindly provided the monitoring data used in this paper. Semeion Research Center of Sciences of Communication, is also thanked for providing the specialist ANNs software for all the elaborations and funded MB and GM for this research. AB benefited from funding provided by the MED-SUV project. The MED-SUV project has received funding from the European Union Seventh Framework Programme (FP7) under Grant agreement no. 308665. We are grateful to two anonymous reviewers, whose constructive comments greatly improved the manuscript.
NOTES
![]()
*Corresponding author.