A Simple Closed Form Solution to Single Layer Heat Spreading Angle Appropriate for Microwave Hybrid Modules ()
Received 26 April 2016; accepted 12 June 2016; published 15 June 2016
1. Introduction
Heat transfer analysis and design is an important step in the development of a product or system that contains electronics. This is due to the fact that long term reliability of semiconductor electronics depends, in part, on the temperature of the electronic device. Prior to detailed thermal analysis using 3D numerical methods, such as finite element or finite difference methods, it is common for engineers to perform trade studies using simplified closed form equations for quick estimations of thermal resistances and temperature rises. Trade studies allow rapid assessment of the impact of changes to packaging materials and operating conditions of the electronics so that the detailed numerical simulation effort can have a reasonable design starting point. The desire for rapid analysis has motivated numerous researchers to develop closed form approximations for heat transfer.
For instance, a constant spreading angle method was used to generate a closed form equation for heat spreading assuming there was a spreading section and non-spreading section [1] in the heat spreader. Another team developed a set of equations for heat transfer in integrated circuits [2] . Some have performed thermal modeling with the assumption that the spreading angle is 45 degrees [3] . Others have rejected the 45 degree spreading angle assumption all together [4] [5] , and some have used other spreading angles of 32.5 degrees [6] or 26.6 degrees [7] claiming that they are a more accurate approximation. The point is that multiple efforts have been made to develop methods for simplified and rapid estimation of heat transfer and thermal resistance using the concept of heat spreading and spreading angle with varying degrees of accuracy. More complex methods have been developed too with good summaries in [8] - [12] .
This work continues the effort to develop a closed form equation for rapid estimation of thermal resistance to model the case of a rectangular heat source attached to a single layer heat spreader over a heat sink. As will be seen, the main benefit of our approach is the extreme simplicity of the resulting closed form equation for calculating heat spreading angle. It can be easily implemented in a spread sheet for quick trade study analysis.
A cross-section of the configuration being considered here is illustrated in Figure 1. The method developed maintains a tight connection to the physical structure so that valid insights into heat spreading can be achieved. A definition of the variable used is given in Table 1.
![]()
(a) (b)
Figure 1. Illustration showing (a) cross-section of a heat source over a large heat spreader connected to an isothermal heat sink, and (b) the equivalent circuit.
im = meter, W = Watt, K = Kelvin, ˚C = degree Celsius.
Section 2 presents the motivation for the present investigation which is to develop a simplified analysis method for spreading angle for single layer heat spreaders connected to a cold plate. This is a common configuration of microwave hybrid modules. Section 3 shows the derivation of the temperature rise equation using methods developed in [7] [13] - [14] . In Section 4, finite element method (FEM) heat spreading simulation results are examined. The spreading angle introduced in the previous section can be found by performing an error minimization routine to achieve agreement to within 10−5 percent error. In Section 5, the equation of spreading angle is derived which avoids the need for the error minimization method. This is accomplished by recognizing that the spreading angle equation is quadratic which leads to a closed form solution. The spreading angle is derived as a function of the physical features, materials, and temperature rise. In Section 6, the spreading angle equation is simplified for the special case of a square heat source. We take this step because it leads to a compact equation of heat spreading that more easily provides insight into heat spreading. Once this is completed, Section 6 discusses the valid ranges for the derived equations. Section 7 provides an explanation of why the spreading angle is not a function of thermal conductivity once the physical dimensions are set. Section 8 gives a curve fit equation for spreading angle that is only a function of the physical dimensions of the heat source and heat spreader thickness. A step by step procedure is presented for using this method and illustrates it with five different simulation cases. Section 9 is the conclusion with a summary and assessment.
2. Motivation from Microwave Hybrids
It is common practice for GaAs and GaN integrated circuits used in microwave hybrid modules to be mounted to a heat spreader which is mounted to a cold plate. This case is illustrated in Figure 1. In these cases, engineers normally make two simplifying assumptions in their initial thermal analysis prior to 3D numerical simulations. The assumptions are:
1) The heat generated by the semiconductor integrated circuit is uniform at the point it contacts the heat spreader.
2) The heat is spread at an assumed angle within the heat spreader. Some engineers prefer to be conservative and assume zero heat spreading angle. Others will assume a more optimistic 45 degree spreading angle.
These assumptions permit the microwave hybrid module designer to perform quick trade studies to determine if the material chosen and physical configurations have a chance of providing the thermal performance that is required. Once a material set is chosen the module designer passes the information off to the thermal analyst who performs the 3D numerical simulations.
The motivation for this work is to provide the practicing microwave module hybrid designer with a simple closed form equation that can be used to estimate heat spreading angle. This will allow for more accurate initial trade studies prior to detailed thermal simulations.
Since the motivation for this solution is a microwave hybrid module we make the simplifying assumption of only conduction and neglect any convection that may be occurring in the module. However, since most microwave hybrid modules are hermetically sealed, this assumption will not significantly limit the usefulness of the results of this work.
3. Temperature Rise in a Single Layer
We know from Fourier’s Heat Transfer Law that the heat flow, Q, normal to a heat transfer area, A, can be found from the thermal conductivity, k, multiplied by the derivative of the temperature with respect to the direction of heat flow. This situation is illustrated in Figure 2. Fourier’s equation can be written as
![]()
Figure 2. Illustration showing that there is a temperature rise of ΔT = T2 − T1 in the direction of heat flow.
(1)
which can be re-arranged to solve for the temperature rise from T1 to T2 to obtain
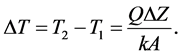(2)
where ∆Z describes the distance between two nodes (T2 and T1) with a thermal profile, and A = X・Y which is the area of the heat source. This means that (2) can be re-written as
(3)
Returning our attention to Figure 1, we realize that in any practical instance of a heat source over a heat spreader, the area of the heat source will have finite extent in both the x and y-directions. This is illustrated in Figure 3 and shows that as the heat is transferred from the source to the bottom of the heat spreader (in the z- direction), dimension X extends to become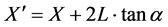 
and Y extends to become
. This means the effective area of the heat source increases at the bottom of the heat spreader to
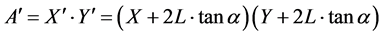(4)
This area, A', is the same area A from (2). Substituting (4) into (3) and recognizing that ΔZ = L, we obtain:
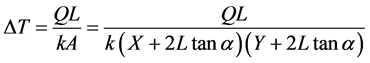(5)
4. Comparison of Closed Form Equation to Finite Element Simulation Results
As a method of verifying the accuracy of (5), a series of simulations were conducted using the FEM. To simplify the analysis, we made the assumption that the heat source is a square (i.e. X = Y) of fixed dimension and that the heat spreader extended in the x and y-directions at least 10 times the thickness so that the finite extent of the heat spreader would have negligible effect on the simulations. We used a varying material thermal conductivity, k, of 0.1 to 2000 W/mK and varying thickness, L, of 0.127mm to 20.32mm. The solution for the temperature rise in the heat spreader, ΔT, was recorded for each simulation assuming a mounting temperature, TA, of 0˚C. Additionally, convection is neglected when simulating due to the minimal effects it has on ΔT. The values of thermal conductivity and thickness were chosen to encompass a wide range of materials encountered in the manufacturing of electronic packaging. There were 207 FEM simulations performed and they are summarized in the Appendix as Table 5.
![]()
Figure 3. Sketch of a heat source over a single layer heat spreader with a spreading angle (α = spreading angle, L = thickness of the heat spreader, X・Y = Area of the heat source, Q = dissipated heat in Watts).
The values of ΔT from FEM analysis and (5) were compared to check for accuracy. Of course, the challenge is to know the value of the spreading angle, α, with a provided L that gives the best agreement. We employed a type of error function and minimized the error to obtain α. If the values of ΔT from (5) are referred to as ΔT(5), and if the values of ΔT from FEM are referred to as ΔTFEM, and if we sum the squares of the error as a function of the thermal conductivity, then the error function will be
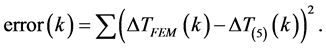(6)
This procedure was followed for the case of a square heat source with X = Y = 2.54 mm and L = 2.54 mm, Q = 10 W, and TA = 0˚C and the results are summarized in Table 2. It is important to note that the spreading angle, α, is constant as a function of thermal conductivity, k. As can be seen, the error between the FEM predicted values of ΔT and those predicted by (5) agree within about 5 significant digits or better over the range of thermal conductivity from 0.1 to 2000 W/mK.
When the minimization of (6) was applied to all the other values of ΔTFEM in Table 5, similar levels of agreement were achieved except for thin heat spreader layers less than equal to approximately 0.0127 mm. The best agreement is for heat spreader greater than 0.330 mm thick. The reader is encouraged to notice that the spreading angle used in Table 2 is the same for all values of thermal conductivity.
5. Spreading Angle Derivation for Rectangular Heat Source
Most GaAs and GaN devices are rectangular. Therefore, our analysis in this section assumes the heat source is rectangular. Not only is this appropriate since it matches the actual configuration of the integrated circuits, setting the heat source as rectangular is convenient for analysis reasons. A rectangular heat source assumption simplifies the equation for heat spreading.
The goal of this section is to derive an equation for the spreading angle. This will allow for direct calculation of the spreading angle. We start by rearranging (5) to obtain
![]()
Table 2. Comparison of FEM Results and Predictions Using (5).
iUsing α = 13.62 degrees obtained from minimization of (6).
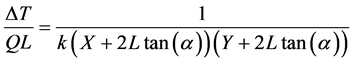(7)
where ΔT = T − TA. This can be simplified and multiplied through to obtain
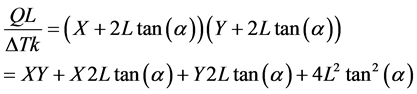(8)
As can be seen, (8) is a second order equation with respect to tan(α). If it is rearranged appropriately, the quadratic equation can be used to solve for tan(α) which will yield the angle α. Rearranging (8) we obtain
![]()
(9)
Which can be rearranged into a quadratic form as
![]()
(10)
It should be immediately recognized that (10) is in the familiar form of a quadratic equation which can be solved using the quadratic formula. This immediately leads to a solution for tan(α), and we obtain
![]()
(11)
When using the quadratic formula, two roots, or two angles are calculated. We have found the correct solution is obtained when using the positive value of the rooted discriminant which leads to the solution for the spreading angle
![]()
(12)
which is used when the dimensions of the heat source are rectangular where X ≠ Y. In the next section we will simplify (12) for the case of a square heat source since it can provide some insight into the physics of heat spreading.
6. Special Case: Spreading Angle for Square Heat Source
The equation for spreading angle for the case of a square heat source can be obtained by using (11) and setting X=Y. If this is done, and if the positive value of the rooted discriminant is taken, then (12) becomes
![]()
(13)
As a verification of the validity of (13), it was used to calculate the spreading angle for the case shown in Table 2. The spreading angle was calculated for every case of thermal conductivity shown in the table. If N represents the number of thermal conductivity values used, and ![]()
are each of the spreading angles calculated, then the average spreading angle is found using
![]()
(14)
where the αj(k) are the values of α obtained for each of the thermal conductivity values over the range of interest using (13). The results are shown in Table 3 which shows that the average value for spreading angle is 13.623 which is the same value that was used in Table 2 and obtained from the minimization of (6).
It should be kept in mind that the spreading angle of 13.62 degrees is only applicable to this specific case and is not meant to be universally applied spreading angle. The challenge of determining the spreading angle without needing the value of ΔT is examined in Section 8 where a curve fit equation is provided that only depends on the physical dimensions of the heat source and spreader. It is also important to note that the standard deviation in α using (13) and (14) is only 0.00145 which shows that there is an extremely weak dependence of spreading angle upon thermal conductivity (within calculation error) for a fixed value of physical dimensions of the heat source and heat spreader.
The comparisons with 3D FEM analysis has shown that (5), (12), and (13) are accurate for thicknesses of heat spreaders that are greater than about 0.330 mm for most practical values of thermal conductivity (0.1 to 2000 W/mK). However, for small values of thermal conductivity (less than approximately 10 W/mK) we found (5), (12) and (13) still supplied trustworthy results.
For thin heat spreaders (less than 0.381 mm) and higher thermal conductivity (>10 W/mK), the error manifests as what appears to be nonphysical variations in predicted spreading angle using (12) or (13).
7. Explanation of Spreading Angle as a Function of Thermal Conductivity
One of the interesting results of FEM modeling and predicted α using (12) and (13) is that for a fixed set of physical dimensions, the spreading angle is constant as a function of thermal conductivity for the single layer case being considered in this work. Table 2 shows this result since the calculated ΔT(5) uses the same angle for all values in the table. This is also shown more explicitly in Table 3 which shows all the αj(k)(13) are essentially the same (to within 4 significant digits) as thermal conductivity varies from 0.1 to 2000 W/mK. Note that αj(k)(13) are the αj(k) calculated using (13) and α(14) is the average value calculated using (14).
![]()
Table 3. Example calculation of average α using (14).
For X = Y = 2.54 mm, L = 2.54 mm, Q = 10 W.
However, upon initial inspection of (12) and (13), it is immediately evident that the spreading angle, α, is proportional to the square root of thermal conductivity. There seems to be some contradiction between those two equations and the tables which show a very weak, or zero, dependence of ΔT as a function of k. Resolution of the contradiction is evident upon closer inspection. Consider (14) and the variables under the square root. Since ΔT is inversely proportional to thermal conductivity, k, the product of ΔT and k cancels its’ contribution to the spreading angle. For this reason, the spreading angle is independent of thermal conductivity of the spreader.
8. Curve Fit Equation for Heat Spreading and 3-Step Procedure
The analysis has shown that (5), (12), and (13) are accurate when compared to FEM simulations. However, the obvious difficulty in using (12) or (13) is that they require knowledge of the temperature rise in order to calculate the spreading angle. However, that is rarely known initially. Therefore, a method of calculating an approximated spreading angle would be useful. Therefore, we have developed a curve fit equation based on TFEM data for the special case of X = Y = 2.54 mm. It was found that a good curve fit equation is the exponential function
![]()
(15)
where P is the Normalized Dimension Parameter and is given by P = L/(X + Y). The error in using (15) for calculating the spreading angle was found to be less than 4.5% over the range of L/(X + Y) of 0.0725 to 4.0. The plot of the spreading angle and the curve fit are shown in Figure 4. Using (15) to calculate spreading angle permits the use of (5) to determine the temperature rise in the heat spreader.
The method presented here can be used in a systematic way to predict the heat transfer in single layer heat spreading. The step by step procedure is:
Step 1: Calculate the Normalized Dimension Parameter, P, from the physical dimensions of the heat source and the thickness of the heat spreader, X, Y, and L.
Step 2: Using P and (15) calculate the spreading angle, α.
Step 3: Using the spreading angle, α, and (5), calculate the temperature rise in the heat spreader, ΔT.
This procedure was used in five cases with a rectangular heat source to check for accuracy. The results are shown in Table 4. Note that error in this procedure is less than about 8% which will improve with a more accurate curve fit (15).
![]()
Figure 4. Spreading angle, a, as a function of L/(X + Y) from (12) (solid line) and curve fit (15) (dashed line).
![]()
Table 4. Comparison of FEM results to proposed procedure.
For Q = 10 W, k = 100 W/mK, ErrorT between ΔTFEM and ΔT(5).
9. Conclusions
We have shown that a simplified equation for heat spreading angle can be developed. We also showed that it is accurate over a broad range of physical dimensions and thermal conductivity for the heat spreader. This will mean that the very simple spreading angle equation can be of practical use to engineers developing microwave hybrid modules.
More work should be conducted on this approach. In particular, additional analysis could be performed to determine the range of accuracy with more precision. This would require a greater number of simulations that funding for this project can support. An improvement of (15) for accuracy of predicting the spreading angle, α, would improve the accuracy of procedure.
Appendix
![]()
Table 5. Finite Element Modeling (FEM) results yielding ΔTFEM with X = Y = 2.54 mm.