Decomposition of Generalized Asymmetry Model for Square Contingency Tables

Shuji Ando¹, Hiroyuki Kurakami²

¹Data Management & Biostatistics Group Re-Examination Department, Novartis Pharma K.K., Tokyo, Japan.
²Department of Information Sciences, Faculty of Science and Technology, Tokyo University of Science, Chiba, Japan.

DOI: 10.4236/ojs.2016.63036                

Abstract

For the analysis of square contingency tables with same row and column ordinal classifications, the present paper gives the decomposition of the generalized linear diagonals-parameter symmetry model using the diagonals-parameter symmetry model. Moreover, it gives the decomposition of the symmetry model using above the proposed decomposition.

Keywords

Diagonals-Parameter Symmetry, Linear Diagonals-Parameter Symmetry, Orthogonality, Symmetry

Received 18 April 2016; accepted 11 June 2016; published 14 June 2016

1. Introduction

Consider an 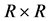square contingency table with the same row and column classifications. Let 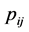denote the probability that an observation will fall in the ith row and jth column of the table (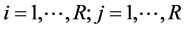). For square tables with ordered categories, Goodman [1] proposed the diagonals-parameter symmetry (DPS) model, defined by

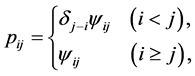
where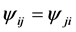. Note that the DPS models with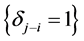, , 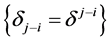and 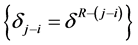are identical

to the symmetry (S) (Bowker [2] ), linear diagonals-parameter symmetry (LDPS) (Agresti [3] ), and another LDPS (ALDPS) (Tomizawa [4] ) models, respectively.

Yamamoto and Tomizawa [5] proposed the generalization of LDPS model. We will denote 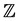as the set of integers. For a fixed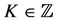, the generalized LDPS (LDPS(K)) model is defined by

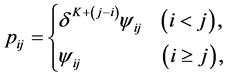
where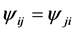. Note that the LDPS(K) model with is identical to the S model. Especially the LDPS(0) and LDPS(-R) models are equivalent to the LDPS and ALDPS models, respectively.

Tomizawa [6] gave the decomposition of the LDPS model using the DPS model, and showed that a test statistic for the LDPS model was equal to the sum of those for decomposed models.

For the analysis of square contingency tables with ordered categories, the purposes of this paper are (1) to give the decomposition of the LDPS(K) model using the DPS model, (2) to show that for the test statistic for the LDPS(K) model is equal to the sum of those for decomposed models, and (3) to give the decomposition of the S model using above the decomposition of the LDPS(K) model.

2. Decomposition of the Generalized Asymmetry Model

Tomizawa [6] proposed the linear diagonals-parameter marginal symmetry (LDPMS) model, defined by

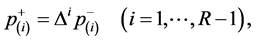
where

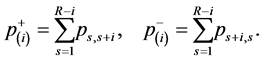
Let X and Y denote the row and column variables, respectively. The LDPMS model indicates that is times higher than for all. Under LDPMS model, if then , and if then.

Also, Tomizawa [6] gave the decomposition of the LDPS model using the DPS and LDPMS models, and showed that a test statistic for the LDPS model is equal to the sum of those for the DPS and LDPMS models.

To consider the decomposition of the LDPS(K) model, we shall introduce a new model. For a fixed, the generalized LDPMS (LDPMS(K)) model is defined by

Especially the LDPMS(0) model is equivalent to the LDPMS model.

We will denote as the set of integers of or less, as the set of integers from to, and as the set of integers of or greater. Under the LDPMS(K) model with a fixed, if then. Also, under the LDPMS(K) model with a fixed, if, there exists a certain t such that for and for. Moreover, under the LDPMS(K) model with a fixed, if then .

We obtain the following theorem.

Theorem 1. For a fixed, the LDPS(K) model holds if and only if both the DPS and LDPMS(K) models hold.

Proof. If the LDPS(K) model holds, then the DPS and LDPMS(K) models hold. Assuming that both the DPS and LDPMS(K) models hold, then we shall show that the LDPS(K) model holds.

From the LDPMS(K) model holds, we obtain

Also, from the DPS model holds, we see

Therefore, we obtain for all. Namely, the LDPS(K) model holds. The proof is com- pleted.

3. Orthogonality of Test Statistic and Model Selection

Assume that a multinomial distribution applies to the table. Let denote the observed frequency in the ith row and jth column of the square table (), with. The maximum likelihood estimates (MLEs) of expected frequencies under the model could be obtained by using, e.g., the Newton-Raphson method in the log-likelihood equation.

Each model can be tested for goodness-of-fit by, e.g., the likelihood ratio chi-square statistic (denoted by) with the corresponding degrees of freedom (df). The test statistic of model M is given by

where is the MLE of expected frequency under model M. The number of df for LDPMS(K) model is, which is equal to that for LDPMS model.

A quick method for choosing the best-fitting model among different models is to use Akaike’s [7] information criterion (AIC), which is defined as

for each model. For more details of AIC, see Konishi and Kitagawa [8] . This criterion gives the best-fitting model as the one with minimum AIC. Since only the difference between AICs is required when two models are compared, it is possible to ignore a common constant of AIC and we may use a modified AIC defined as

Thus, for the data, the model with the minimum AIC⁺ (i.e., the minimum AIC) is the best-fitting model.

For the analysis of contingency tables, Read [9] discussed the orthogonality, which is equivalent to the asymptotic separability in Aitchison [10] and the independence in Darroch and Silvey [11] of test statistic for goodness-of-fit of two models.

On the orthogonality of test statistic for models in Theorem 1, we obtain the following theorem.

Theorem 2. For a fixed, the following equation holds:

The number of df for the LDPS(K) model equals the sum of number of df for the DPS and LDPMS(K) models.

Proof. First, we consider that the MLEs of expected frequencies under the LDPS(K) model are given by

where is the solution of the following equation

(3.1)

with

We can solve (3.1) for by using the Newton-Raphson method.

Second, we consider that the MLEs of expected frequencies under the DPS model are given by

where.

Last, we consider that the MLEs of expected frequencies under the LDPMS(K) model are given by

where is the solution of the Equation (3.1) with replaced by. Thus, we see that under the LDPS(K) model is equal to the product of under the DPS model and that under the LDPMS(K) model. Therefore, the test statistic for goodness-of-fit for LDPS(K) model is equal to the sum of those for two models. The proof is completed.

4. Decomposition of the Symmetry Model

For square contingency tables with ordered categories, Kurakami, Yamamoto and Tomizawa [12] considered two models. One is the generalized exponential symmetry (GES) model defined by

where and are the specified non-negative values. The other is the generalized weighted global symmetry (GWGS) model defined by

For a fixed, the GES model with non-negative values is identical to the LDPS(K) model. For a fixed, because are non-negative values, the LDPS(K) model is included in the GES model. Note that for a fixed, the LDPS(K) model is not included in the the GES model, because have both positive and negative values. For a fixed, we shall refer to the GWGS model with as the WGS(K) model.

Kurakami et al. [12] also gave the decomposition of the S model using the GES and GWGS models, and showed that a test statistic for the S model is approximately equivalent to the sum of those for the GES and GWGS models.

We will denote as the set of non-negative integers. Yamamoto, Ohama and Tomizawa [13] gave the following theorems.

Theorem 3. For a fixed, the S model holds if and only if both the LDPS(K) and WGS(K) models hold.

Theorem 4. For a fixed, the following asymptotic equivalence holds:

The number of df for the S model equals the sum of the number of df for the LDPS(K) and WGS(K) models.

From the theorems given by Kurakami et al. [12] , we obtain the following theorems as extensions of Theorems 3 and 4 (because the includes).

Theorem 5. For a fixed, the S model holds if and only if both the LDPS(K) and WGS(K) models hold.

Theorem 6. For a fixed, the following asymptotic equivalence holds:

The number of df for the S model equals the sum of the number of df for the LDPS(K) and WGS(K) models.

From Theorems 1 to 6, we obtain the following corollaries.

Corollary 1. For a fixed, the S model holds if and only if all the DPS, LDPMS(K) and WGS(K) models hold.

Corollary 2. For a fixed, the following asymptotic equivalence holds:

The number of df for the S model equals the sum of the number of df for the DPS, LDPMS(K) and WGS(K) models.

5. An Example

Consider the data in Table 1, taken directly from Bishop, Fienberg and Holland ( [14] , p. 100). From Table 2, all LDPS(K) models, the S model and DPS model give poor fits to these data. However, all LDPMS(K) models fit these data well.

The LDPMS(2) model is the best-fitting model among the other LDPMS(K) models because it has a mini- mum AIC⁺ value. Under the LDPMS(2) model, the MLE of is. Thus, we see that the status category for a father tends to be less than that for his son.

Theorem 1 would be useful for seeing the reason for its poor fit when the LDPS(K) model fits the data poorly. Thus, for the data in Table 1, the poor fit of the LDPS(K) model is caused by the poor fit of the DPS model rather than the LDPMS(K) model. Also, Theorem 5 would be useful for seeing the reason for its poor fit when the S model fits the data poorly. From Table 2, WGS(K) models (except the WGS(−1) model) give poor fits to these data. Thus, when K is not equal to −1, we cannot see that the poor fit of the S model is caused by the poor fit of either LDPS(K) and WGS(K) models (although, we can see that the poor fit of the S model is caused by the poor fit of both LDPS(K) and WGS(K) models). However, using Corollary 1, we can see that the poor fit of

Table 1. Occupational status for Danish father-son pairs; from Bishop et al. ( [14] , p. 100) (The parenthesized value is MLEs of expected frequencies under the LDPMS (2) model).

Note: Status (1) is high professionals, (2) White-collar employees of higher education, (3) White-collar employees of less high education, (4) Upper working class, and (5) Unskilled workers.

Table 2. Likelihood ratio chi-square values G² and AIC⁺ for models applied to the data in Table 1.

^*Means significant at the 0.05 level.

the S model is caused by the poor fit of DPS and WGS(K) models rather than the LDPMS(K) model.

6. Concluding Remarks

We have given the decomposition of the LDPS(K) model using the DPS model (namely, Theorem 1). Also, we have shown that the test statistic for the LDPS(K) is equal to the sum of those for the decomposed models (namely, Theorem 2). Moreover, we have given the decomposition of the S model using Theorem 1 (namely, Corollary 1), and shown that the test statistic for the S model is approximately equivalent to the sum of those for the decomposed models (namely, Corollary 2). Although details will be omitted, Yamamoto, Ohama and Tomizawa [15] gave the another decomposition of the the LDPS(K) model for a fixed. However, it does not hold the orthogonality of test statistic for models. Thus, Theorem 1 may be useful for analyzing the data than the decomposition by Yamamoto et al. [15] . Because Theorem 1 shows the decomposition of LDPS(K) for a fixed (because includes), and also holds the orthogonality of test statistic for models.

Acknowledgements

We thank the reviewer for the helpful comments. Also, we thank Professor S. Tomizawa and Dr. K. Tahata of Tokyo University of Science for their useful suggestions.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Goodman, L.A. (1979) Multiplicative Models for Square Contingency Tables with Ordered Categories. Biometrika, 66, 413-418. http://dx.doi.org/10.1093/biomet/66.3.413
[2]	Bowker, A.H. (1948) A Test for Symmetry in Contingency Tables. Journal of the American Statistical Association, 43, 572-574. http://dx.doi.org/10.1080/01621459.1948.10483284
[3]	Agresti, A. (1983) A Simple Diagonals-Parameter Symmetry and Quasi-Symmetry Model. Statistics and Probability Letters, 1, 313-316. http://dx.doi.org/10.1016/0167-7152(83)90051-2
[4]	Tomizawa, S. (1990) Another Linear Diagonals-Parameter Symmetry Model for Square Contingency Tables with Ordered Categories. South African Statistical Journal: Journal of the South African Statistical Association, 24, 117-125.
[5]	Yamamoto, K. and Tomizawa, S. (2012) Statistical Analysis of Case-Control Data of Endometrial Cancer Based on New Asymmetry Models. Journal of Biometrics and Biostatistics, 3, 1-4. http://dx.doi.org/10.4172/2155-6180.1000147
[6]	Tomizawa, S. (1990) A Decomposition of Linear Diagonals-Parameter Symmetry Model for Square Contingency Tables with Ordered Categories. Biometrical Journal, 32, 761-766. http://dx.doi.org/10.1002/bimj.4710320619
[7]	Akaike, H. (1974) A New Look at the Statistical Model Identification. IEEE Transactions on Automatic Control, AC- 19, 716-723. http://dx.doi.org/10.1109/TAC.1974.1100705
[8]	Konishi, S. and Kitagawa, G. (2008) Information Criteria and Statistical Modeling. Springer, New York. http://dx.doi.org/10.1007/978-0-387-71887-3
[9]	Read, C.B. (1977) Partitioning Chi-Square in Contingency Table: A Teaching Approach. Communications in Statistics-Theory and Methods, 6, 553-562. http://dx.doi.org/10.1080/03610927708827513
[10]	Aitchson, J. (1962) Large-Sample Restricted Parametric Tests. Journal of the Royal Statistical Society, Series B, 24, 234-250.
[11]	Darroch, J.N. and Silvey, S.D. (1963) On Testing More than One Hypothesis. Annals of Mathematical Statistics, 34, 555-567. http://dx.doi.org/10.1214/aoms/1177704168
[12]	Kurakami, H., Yamamoto, K. and Tomizawa, S. (2011) Generalized Exponential Symmetry Model and Orthogonal Decomposition of Symmetry for Square Tables. The Open Statistics and Probability Journal, 3, 1-6. http://dx.doi.org/10.2174/1876527001103010001
[13]	Yamamoto, K., Ohama, M. and Tomizawa, S. (2013) Decompositions of Symmetry Using Generalized Linear Diagonals-Parameter Symmetry Model and Orthogonality of Test Statistic for Square Contingency Tables. Open Journal of Statistics, 3, 9-13. http://dx.doi.org/10.4236/ojs.2013.36A002
[14]	Bishop, Y.M.M., Fienberg, S.E. and Holland, P.W. (1975) Discrete Multivariate Analysis: Theory and Practice. The MIT Press, Cambridge.
[15]	Yamamoto, K., Ohama, M. and Tomizawa, S. (2015) Vision Data Analysis Based on New Statistical Models and Decompositions. Annals of Biometrics and Biostatistics, 2, 1-7.