Characterizing Subzero-Temperature Thermal Properties of Seasonally Frozen Soil in Alpine Forest in the Western Sichuan Province, China

Hui Sun¹, Shuai Liu², Jihong Qin^3*

¹Department of Environmental Science and Engineering, Sichuan University, Chengdu, China.
²Institute of Soil Science, Chinese Academy of Sciences, Nanjing, China.
³Department of Environmental Engineering, College of Urban and Rural Construction, Chengdu University, Chengdu, China.

DOI: 10.4236/jwarp.2016.85048                

Abstract

Seasonally frozen soil in alpine and subalpine zones in the mountains of Qinghai-Tibetan Plateau is particularly sensitive to global climate change. Therefore, a better understanding of the thermal properties of frozen soil is crucial for predicting the responses of frozen soils to soil warming. In this study, thermal properties of frozen soil with different moisture contents under subzero temperature (0°C - 20°C) in an alpine forest in western Sichuan were analyzed by KD₂ Pro in its cooling and heating processes, respectively. Our results reveal that the soil apparent volumetric specific heat capacity (C_v) and apparent thermal conductivity (K) under the same water content show similar response patterns to changing temperature lower than -2°C in both heating and cooling processes. Moreover, ice content of frozen soils can be well predicted by Logistic model in cooling and heating processes. The C_v and K tend to increase along with increasing soil moisture contents. Remarkably, asymptotic characters of the value of C_v and K are at the vicinity of the initial temperature of phase transitions, indicating that both C_v and K are particularly sensitive to changing soil temperature at the range of -2°C to 0°C. Therefore, the widely distributed frozen soil layers with temperature above -2°C in alpine and subalpine zones over Qinghai-Tibetan Plateau are susceptible to the observed climate warming during cold season.

Keywords

Alpine Soil, Seasonally Frozen Soil, Thermal Properties, Qinghai-Tibetan Plateau

Received 30 November 2015; accepted 17 May 2016; published 20 May 2016

1. Introduction

Approximately 50% of the land surface in high altitudes and latitudes of Northern Hemisphere is characterized by seasonally frozen ground, with more than 25% estimated to be covered by permafrost [1] . Thawing and freezing processes of the seasonally frozen soils have large effects onland-atmosphereenergy exchangesand hydrological processes [2] . Soil freezing reduces the soil water potential considerably because soil retains unfrozen water, leading to steep changes of hydraulic gradient and redistribution of soil water and solute. Therefore, having a basic knowledge of thermal properties is crucial to frozen soil and accurate measurements of the soil thermal properties are fundamental for most models to parameterize the transformation processes of thawing-freezing cycles in these cold soil ecosystems [3] [4] . Moreover, understanding the soil thermal properties with different soil temperature and moisture plays an important role in determining ecological changes and predicting future responses of seasonally frozen and permafrost soil to the rapid climate warming [5] .

Phase changes of soil water below 0˚C lead to specific heat capacity change and latent heat transformation, hence total soil water, including both ice and liquid water, has profound influences on the soil hydraulic, thermal and mechanical properties [6] [7] . Freezing of soil moisture reduces the hydraulic conductivity, interrupts the infiltration of rainfall or snowmelt, and increases surface runoff, leading to thawing erosion and nutrient loss [8] [9] , especially in earlier spring. In order to have a better understanding to the processes in soil freeze-thaw cycles, many different methods are established for determining unfrozen water and ice content of frozen soils, including dilatometry [10] , suction-moisture relationship [11] , nuclear magnetic resonance (NMR) [12] , time domain reflectometry (TDR) [13] , and neutron and gamma ray method [14] . However, these methods have their respective disadvantages [4] [15] . Clearly, it is necessary to establish a simple method for estimating water and ice contents in frozen soils accurately.

In fact, soil thermal property is originated by a complex combination of conductive processes and intra-porous convection processes, besides they are related to soil water phase change. We then prefer to be more concerned with the apparent soil thermal properties and discuss the ice content of frozen soils. Recently, a heat pulse probe (HPP) method was developed and proven to be a promising technology for measuring soil apparent thermal properties, water and ice contents and snow density [16] [17] . The KD₂ Pro is a novel device with small size based on HPP method which can be used for measuring all three soil thermal properties in situ simultaneously under a rapid nondestructive way at both laboratories and fields, while minimizing the device-induced water movement and free convection. The ability of KD₂ Pro had been proven in many studies of measurements of thermal properties for different types of unfrozen soils [18] [19] , and frozen or permafrost soils [20] .

Permafrost and seasonally frozen soil in Qinghai-Tibetan Plateau and high mountains in the western China occupy the largest area of the high altitudinal lands of the Northern Hemisphere [21] Moreover, the Qinghai-Tibetan Plateau, which is proven to be the most sensitive regions to climate change, is experiencing rapid climate warming in recent decades especially during cold seasons, which resulting in noticeable degradation of permafrost [22] , and abrupt changes of freeze-thaw patterns in the seasonally frozen soil in recent thirty years [23] . However, there are few reports on the responses of soil apparent thermal properties to changing climate in subalpine and alpine zones of Qinghai-Tibetan Plateau. Therefore, in this study we try to analyze the thermal properties of seasonally frozen soil and their linkage to different soil water contents in cooling and heating processes under subzero temperature (−20˚C - 0˚C).

2. Materials and Methods

2.1. Soil Samples

Soil sampling site is located at Mt. Mengbi (31˚33.25'N, 102˚24.92'E, elevation 3250 m ), which is located between the north section of Qionglai Mountains and Daxue Mountains in the northwest of Sichuan Province. The sampling site is dominated by the mountainous monsoon climate with a cool-rainy summer and cold-dry winter. The mean annual temperature and total annual precipitation are 8.6˚C and 760 mm , respectively. The alpine coniferous forest and mixed forest with the dominant species of Abies faxoniana and Picea balfouriana are distributed from elevation of 3000 m to 4300 m. The sampled soil is organic loamy sand and classified as mountain brown coniferous forest soils [24] , and topsoil (0 - 40 cm) is frozen in the cold season from October to next May.

Forest topsoil (0 - 20 cm layer) is collected, homogenized, and sieved through a 2 mm mash screen to remove gravel, litter materials and fine roots. The sieved homogenized soil is repacked into cylindrical PVC columns with 5 cm in diameter and 20 cm in height keeping its original bulk density. The repacked soil columns are pre-incubated in situ under the natural conditions of alpine forest for three years. Soil samples were collected in July 2014. Before measurement, soil columns packed in PVC container were collected and placed into coolers and transported to laboratory within 24 hours. Soil columns for thermal property measurement were sampled and examined with an oven-dry bulk density of 0.91 g∙cm⁻³ and soil organic carbon content of 139.09 g∙kg⁻¹.

2.2. Measurement and Data Analysis

Soil apparent thermal properties are measured by KD₂ Pro Thermal Properties Analyzer (Decagon Devices, Inc., Pullman, WA). The KD₂ Pro Analyzer takes measurements using the transient line heat source method [25] . Briefly, every measurement cycle consists of a 30-sec equilibrium time, a 30-sec heating time and a 30-sec cooling time. Temperature measurements are made every second during heating and cooling processes, and then temperature measurements are fitted with an exponential integral function using nonlinear least-squares procedure. In general, samples are relatively thin (3 - 4 cm thick), ensuring uniform distribution of water throughout each sample.

Moisture contents of soil columns in PVC container were adjusted and balanced for 2 days, and determined accurately by calculating the weight and volume of soil columns after every measurement, and then wrapped up tightly and carefully by transparent soft film. Wrapped soil column with a certain moisture content was incubated in a thermostatic incubator. The incubation temperature was adjusted and balanced completely before measuring the soil thermal properties. Measurements were performed by inserting the KD₂ Pro probe horizontally into the middle of soil samples with different moisture contents, soil volumetric specific heat capacity and thermal conductivity were recorded during the cooling process (from 0˚C to −20˚C) and subsequently a heating process(from −20˚C to 0˚C) for each soil sample. Three repeated measurements were conducted for each sample during both heating and cooling processes.

Using SPSS statistical software to analyze data.

3. Results and Discussion

3.1. Apparent Volumetric Specific Heat Capacity (C_v) in Cooling and Heating Processes of Frozen Soil

Soil apparent volumetric specific heat capacity (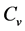) is presented as a function of soil temperature in cooling and heating processes under different moisture contents (Figure 1(A) and Figure 1(B)). The results show that the C_v decreases as initial water contents decrease, and the 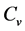values underthe same water content showasimilar response pattern to soil temperatureduring bothheating andcooling processes. One possible reason is that water content is one of dominating factors for 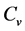under sub-zero temperature, and the frozen soil heat capacities are of attributable to the distribution of ice, voids and mineral materials, and showing a significant decreasing heat capacity with an increase in volumetric fraction of voids in soil will reduce the heat capacity significantly [26] .

We observed a significant change for 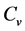when soil temperature near 0˚C (−20˚C - 0˚C). Similar phenomena were also observed by study for the thermal properties of permafrost soil [27] [28] . Previous studies on thermal behaviors of arctic soils have suggested that vapor advection and the associated latent heat effects may contribute to the heat transfer in frozen soils significantly [29] , and latent heat release in phase transition of soil unfrozen water and ice may be the most important contributor to the sharp increase in heating process and the great drop in cooling process of 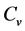when temperature near 0˚C (−20˚C - 0˚C).

We fitted an inverse function for the relationship between 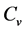and soil temperature ranging from 0˚C to −20˚C. The regression equation was shown in Equation 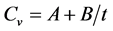(1):

(1)

where A and B are constants, t is soil temperature ranging from −20 to 0˚C, and 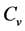is the soil apparent volumetric specific heat capacity. The regression constants of A and B are presented in Table 1.

3.2. Prediction of Unfrozen Water and Ice Content in Soil under Sub-Zero Temperature

Ice, water and soil grain are three main phase diagrams impacting thermal properties of freezing soil [30] ).

Figure 1. Soil apparent volumetric specific heat capacity changes of different moisture content in cooling (A) and heating (B) processes.

Generally, the contribution of air and organic matter can be ignored [31] . Thus, the specific heat capacity (C) of soil can be given by the following equation:

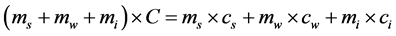(2)

where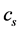, 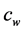and 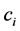are the specific heat capacity of soil particles, soil water and soil ice with unit of MJ∙kg⁻¹∙K⁻¹;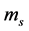, and are masses in kg of soil particles, soil water and soil ice, respectively. The

Table 1. Values of constant A and B of Equation (1) for relationship between C and temperature at different water contents in cooling and heating processes beneath zero temperature.

Note: W_w is initial soil qualitywater contents, A and B are constants in Equation (1). ^* and ^** indicate the variation explained by each model is significant at P < 0.05 level, and significant at P < 0.01 level.

Equation (2), when divided by the total mass of the soil sample, yield

(3)

where W_s, W_w and W_i are percentage quality of soil particles, water and ice, respectively.

Since the apparent volumetric specific heat capacity of moist soil with unit of MJ∙m⁻³∙K⁻¹ is given by; is the bulk density in kg∙m⁻³, and given by

(4)

where is the total volume of the soil sample.

So, Equation (3) can be rewritten in the following equation:

(5)

Then the ice content of frozen soils can be written as

(6)

When T < −10˚C, the vast majority of the unfrozen water is frozen within a few degrees of 0˚C. The unfrozen water content changes very slightly with the initial water content within the range of 1% when the temperature is lower than −10˚C [32] . The mean value of unfrozen water content we determined by the pulsed nuclear magnetic resonance technique is 2.98% as soil temperature below −10˚C with different initial water contents. We use this value asunfrozen water content to calculate soil apparent specific heat capacity and ice content of frozen soils. Equation (5) can be rewritten as

(7)

Then (8)

Generally, the values of and are 4.2 × 10⁻³ MJ/(kg∙K) and 2.1 × 10⁻³ MJ/(kg∙K), respectively. Using Equation (7) and Equation (8) to calculate the value of. After getting those parameters, Equation (6) can be used to figure outice content in frozen soils. Regression equations between soil ice contents and soil temperature are deduced utilizing valid data below −2˚C we calculated. After an ensemble test, the following equation give the best estimation:

(9)

where is initial water content; is percentage quality of ice below 0˚C; a , b and c stand for constants; t is relative temperature measured in laboratory. Residual sum of squares is used as the sensitivity indicator.

All of soils were regressed by Equation (9) for ice content prediction and the values of constants were presented in Table 2 for each soil moisture condition. Soil ice contents of two selected moisture condition were calculated under sub-zero temperature for cooling-heating cycles (Figure 2). It showed that the changing pattern of soil ice contents was not unique between heating and cooling processes due to retention effect during a one-way process of freezing or thawing, i.e., soil ice content may be different at the same temperature in the two processes.

Soil ecosystems in high altitude and latitude are regarded as higher temperature sensitivity to climate change [33] [34] , and the effect of temperature and season on soil microorganisms and enzymes has been addressed by several researchers [34] [35] , and it has been suggested that season-dependent abiotic parameters, such as soil water phase transition and freeze-thaw cycle induced by temperature subzero and above-zero, could influence the microbial community structure [36] [37] ), ecological function, species diversity and respiration activity [33] . In fact, we also found that soil temperature in 5 - 20 cm layer varied between −2˚C and 2˚C in most time in the cold season in the study region (Unpublished data), and a subtle increase of soil temperature could change soil water phases and apparent thermal properties significantly (Figure 1). In that case, soil warming would induce seasonal freezing degradation or disappearance during cold season, which would result in marked changes in ecological functions due to structure and activities of microbial community related to dynamics of soil carbon and nitrogen in seasonally frozen soil.

3.3. Dynamics of Apparent Thermal Conductivity (K) of Frozen Soil

Soil apparent thermal conductivity (K) decreases with the decrease of temperature and soil moisture contents below 0˚C in both cooling and heating processes (Figure 3(A) and Figure 3(B)). During soil freezing, the volumetric expansion of water as well as ice lens tends to change the soil structure and reduce the hydraulic conductivity [26] , and the heat transfer between soil components tends to be weakening. The transport of latent heat may exceed the contribution of heat flow by conduction at temperatures close to 0˚C [38] , and ice melts and soil solution conductivity enhance in heating process. In soil, water is the heat-conducting medium, and it just coats soil particles and voids between the soil particles which are not filled with soil liquid at lower water contents [39] [40] , indicating that there is a strong dependence of the soil thermal conductivity on moisture in freezing soil. Similar results are also observed [41] [42] .

We found that there is also a dramatic change of soil apparent thermal conductivity in the study region from −2˚C to 0˚C whether heating or cooling process (Figure 3(A) and Figure 3(B)). In our study, the thermal conductivity of alpine forest soils tends to decrease within a few degrees below 0˚C in cooling process rather than significant increase as a function of temperature within the range of −15˚C - 0˚C as observed in Ling and Zhang’ study [28] . However, the relationship between thermal conductivity and soil temperature we observed was different from some other studies, Overduin et al. [7] found similar change pattern as our result in thawing process

Table 2. Values of constant a, b and c of Equation (9) for prediction of ice and unfrozen water ratio at different water contents in cooling and heating processes beneath zero temperature.

Note: w_w is initial soil quality moisture contents; a, b and c are constants in Equation (9).

Figure 2. Ice content prediction by Equation (9) in two selected soil moisture in cooling and heating processes under subzero temperature.

below 0˚C with the line heat source, but thermal conductivity data changed adversely in freezing process.

Seigo [43] found that thermal conductivity-temperature line was almost straight in the frozen sate and the empirical formula of temperature from 0˚C to −170˚C was presented in Equation (10).

(10)

where A and B are constant, T is absolute temperature in the study region ranging from 100 kelvin units to 270 kelvin units, K stands for apparent thermal conductivity in freezing soil. In our study, however, the relationship between K and T is presented by the following equation,

(11)

where A and B are constant, T is temperature in centigrade (˚C) in the region ranging from −20˚C to 0˚C.

Values of constant A and B with different moisture contents in our study are presented in Table 3. It is

Figure 3. Soil apparent thermal conductivity changes with different moisture contents in cooling (A) and heating (B) Processes.

considered most likely that constant A is the mean value of soil thermal conductivity when soil temperature is below −10˚C, and we also found that values of A decrease as soil initial water content decrease in cooling process.

Table 3. Values of constant A and B of Equation (11) for relationship between K and temperature at different water contents in cooling and heating processes beneath zero temperature.

Note: W_w is initial soil water contents, A and B are constants in Equation (11). ^* and ^** indicate the variation explained by each model is significant at P < 0.05 level, and significant at P < 0.01 level.

4. Conclusion

We analyzed the relationship between the apparent volumetric specific heat capacity () and apparent thermal conductivity (K) and soil temperature for seasonally frozen soil in alpine zones of the Qinghai-Tibetan Plateau. The results indicate that the values of and K increase as temperature decreases with the same moisture content in cooling or heating processes, and both of them increase with soil water contents within subzero temperature. The asymptotic character of the apparent volumetric thermal capacity and thermal conductivity is at the vicinity of the initial temperature of phase transitions, suggesting the values of and K are particularly sensitive to changes of soil temperature within the range of −2˚C - 0˚C. Moreover, ice content of frozen soils can be well predicted by Logistic model in cooling and heating processes. Our results highlight that soil thermal properties change dramatically near subzero temperature, indicating soil ecological processes may be extremely sensitive to climate warming especially in cold season for the alpine soil in the Qinghai-Tibetan Plateau.

Acknowledgements

This study was funded by National Natural Science Foundation of China (NSFC, No. 41271094 and No. 40871124). We appreciate the anonymous reviewers for their excellent comments that benefit the improvement of this paper.

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Zhang, T., Barry, R.G., Knowles, K., et al. (2003) Distribution of Seasonally and Perennially Frozen Ground in the Northern Hemisphere. Proceedings of the 8th International Conference on Permafrost, AA Balkema Publishers, 2, 1289-1294.
[2]	Zhang, X. and Sun, S. (2011) The Impact of Soil Freezing/Thawing Processes on Water and Energy Balances. Advances in Atmospheric Sciences, 28, 169-177. http://dx.doi.org/10.1007/s00376-010-9206-0
[3]	Henry, H.A.L. (2008) Climate Change and Soil Freezing Dynamics: Historical Trends and Projected Changes. Climatic Change, 87, 421-434. http://dx.doi.org/10.1007/s10584-007-9322-8
[4]	Kojima, Y., Heitman, J.L., Flerchinger, G.N., et al. (2013) Numerical Evaluation of a Sensible Heat Balance Method to Determine Rates of Soil Freezing and Thawing. Vadose Zone Journal, 12. http://dx.doi.org/10.2136/vzj2012.0053
[5]	Schuur, E.A.G. and Abbott, B. (2011) High Risk of Permafrost Thaw. Nature, 480, 32-33. http://dx.doi.org/10.1038/480032a
[6]	Romanovsky, V.E. and Osterkamp, T.E. (2000) Effects of Unfrozen Water on Heat and Mass Transport Processes in the Active Layer and Permafrost. Permafrost and Periglacial Processes, 11, 219-239. http://dx.doi.org/10.1002/1099-1530(200007/09)11:3<219::AID-PPP352>3.0.CO;2-7
[7]	Overduin, P.P., Kane, D.L. and van Loon, W.K.P. (2006) Measuring Thermal Conductivity in Freezing and Thawing Soil Using the Soil Temperature Response to Heating. Cold Regions Science and Technology, 45, 8-22. http://dx.doi.org/10.1016/j.coldregions.2005.12.003
[8]	Cruse, R.M., Mier, R. and Mize, C.W. (2001) Surface Residue Effects on Erosion of Thawing Soils. Soil Science Society of America Journal, 65, 178-184. http://dx.doi.org/10.2136/sssaj2001.651178x
[9]	Zhang, Y., Carey, S.K. and Quinton, W.L. (2008) Evaluation of the Algorithms and Parameterizations for Ground Thawing and Freezing Simulation in Permafrost Regions. Journal of Geophysical Reaseach: Atmospheres, 113. http://dx.doi.org/10.1029/2007JD009343
[10]	Buehrer, T.F. and Rose, M.S. (1943) Studies in Soil Structure V. Bound Water in Normal and Puddled Soils.
[11]	Williams, P.J. (1964) Unfrozen Water Content of Frozen Soils and Soil Moisture Suction. Geotechnique, 14, 231-246. http://dx.doi.org/10.1680/geot.1964.14.3.231
[12]	Kaiser, L.G., Meersmann, T., Logan, J.W., et al. (2000) Visualization of Gas Flow and Diffusion in Porous Media. Proceedings of the National Academy of Sciences, 97, 2414-2418. http://dx.doi.org/10.1073/pnas.050012497
[13]	Spaans, E.J.A. and Baker, J.M. (1996) The Soil Freezing Characteristic: Its Measurement and Similarity to the Soil Moisture Characteristic. Soil Science Society of America Journal, 60, 13-19. http://dx.doi.org/10.2136/sssaj1996.03615995006000010005x
[14]	Bandfield, J.L. (2007) High-Resolution Subsurface Water-Ice Distributions on Mars. Nature, 447, 64-67.
[15]	Hauck, C., Böttcher, M. and Maurer, H. (2011) A New Model for Estimating Subsurface Ice Content Based on Combined Electrical and Seismic Data Sets. The Cryosphere, 5, 453-468. http://dx.doi.org/10.5194/tc-5-453-2011
[16]	Basinger, J.M., Kluitenberg, G.J., Ham, J.M., Frank, J.M., Barnes, P.L. and Kirkham, M.B. (2003) Laboratory Evaluation of the Dual-Probe Heat-Pulse Method for Measuring Soil Water Content. Vadose Zone Journal, 2, 389-399.
[17]	Liu, G. and Si, B.C. (2008) Dual-Probe Heat Pulse Method for Snow Density and Thermal Properties Measurement. Geophysical Research Letters, 35, L16404. http://dx.doi.org/10.1029/2008GL034897
[18]	Tang, A.-M., Cui, Y.-J. and Le, T.-T. (2008) A Study on the Thermal Conductivity of Compacted Bentonites. Applied Clay Science, 41, 181-189. http://dx.doi.org/10.1016/j.clay.2007.11.001
[19]	Smits, K.M., Sakaki, T., Limsuwat, A. and Illangasekare, T.H. (2009) Determination of the Thermal Conductivity of Sands under Varying Moisture, Drainage/Wetting, and Porosity Conditions-Applications in Near-Surface Soil Moisture Distribution Analysis. AGU Hydrology Days.
[20]	Jorgenson, M.T., Romanovsky, V., Harden, J., et al. (2010) Resilience and Vulnerability of Permafrost to Climate Change. Canadian Journal of Forest Research, 40, 1219-1236. http://dx.doi.org/10.1139/X10-060
[21]	Cheng, G.D. and Zhao, L. (2000) The Problems Associated with Permafrost in the Qinghai-Xizang Plateau. Quaternary Sciences, 20, 521-531.
[22]	Wu, T., Zhao, L., Li, R., Wang, Q.X., Xie, C.W. and Pang, Q.Q. (2013) Recent Ground Surface Warming and Its Effects on Permafrost on the Central Qinghai-Tibet Plateau. International Journal of Climatology, 33, 920-930. http://dx.doi.org/10.1002/joc.3479
[23]	Chen, B. and Li, J. (2008) Characteristics of Spatial and Temporal Variation of Seasonal and Short-Term Frozen Soil in China in Recent 50 Years. Chinese Journal of Atmospheric Sciences, 32, 432-443. (In Chinese)
[24]	Gong, Z.T., Zhao, Q.G., Zeng, S.Z., et al. (1978) A Drafting Proposal for Soil Classification of China. Soils, 10, 168-169. (In Chinese)
[25]	Bristow, K.L., Kluitenberg, G.J. and Horton, R. (1994) Measurement of Soil Thermal Properties with a Dual-Probe Heat-Pulse Technique. Soil Science Society of America Journal, 58, 1288-1294. http://dx.doi.org/10.2136/sssaj1994.03615995005800050002x
[26]	Putkonen, J. (1998) Soil Thermal Properties and Heat Transfer Processes Near Ny-Alesund, Northwestern Spitsbergen, Svalbard. Polar Research, 17, 165-179. http://dx.doi.org/10.1111/j.1751-8369.1998.tb00270.x
[27]	Putkonen, J. (2003) Determination of Frozen Soil Thermal Properties by Heated Needle Probe. Permafrost and Periglacial Processes, 14, 343-347. http://dx.doi.org/10.1002/ppp.465
[28]	Ling, F. and Zhang, T. (2004) A Numerical Model for Surface Energy Balance and Thermal Regime of the Active Layer and Permafrost Containing Unfrozen Water. Cold Regions Science and Technology, 38, 1-15. http://dx.doi.org/10.1016/S0165-232X(03)00057-0
[29]	Hinkel, K.M. and Outcalt, S.I. (1993) Detection of Nonconductive Heat Transport in Soils Using Spectral Analysis. Water Resources Research, 29, 1017-1023. http://dx.doi.org/10.1029/92WR02596
[30]	Zhou, J. and Li, D. (2012) Numerical Analysis of Coupled Water, Heat and Stress in Saturated Freezing Soil. Cold Regions Science and Technology, 72, 43-49. http://dx.doi.org/10.1016/j.coldregions.2011.11.006
[31]	Abu-Hamdeh, N.H. (2003) Thermal Properties of Soils as Affected by Density and Water Content. Biosystems Engineering, 86, 97-102. http://dx.doi.org/10.1016/S1537-5110(03)00112-0
[32]	Xu, X., Oliphant, J.L. and Tice, A.R. (1985) Soil-Water Potential and Unfrozen Water Content and Temperature. Journal of Glaciology and Geocryology, 7, 1-14.
[33]	Monson, R.K., Lipson, D.L., Burns, S.P., et al. (2006) Winter Forest Soil Respiration Controlled by Climate and Microbial Community Composition. Nature, 439, 711-714. http://dx.doi.org/10.1038/nature04555
[34]	Wallenstein, M., Allison, S.D., Ernakovich, J., Steinweg, J.M. and Sinsabaugh, R. (2011) Controls on the Temperature Sensitivity of Soil Enzymes: A Key Driver of In situ Enzyme Activity Rates. In: Shukla, G. and Varma, A., Eds., Soil Enzymology, Springer, Berlin, 245-258.
[35]	Lipson, D.A. (2007) Relationships between Temperature Responses and Bacterial Community Structure along Seasonal and Altitudinal Gradients. FEMS Microbiology Ecology, 59, 418-427. http://dx.doi.org/10.1111/j.1574-6941.2006.00240.x
[36]	Koponen, H.T., Jaakkola, T., Keinänen-Toivola, M.M., et al. (2006) Microbial Communities, Biomass, and Activities in Soils as Affected by Freeze Thaw Cycles. Soil Biology and Biochemistry, 38, 1861-1871. http://dx.doi.org/10.1016/j.soilbio.2005.12.010
[37]	Yergeau, E. and Kowalchuk, G.A. (2008) Responses of Antarctic Soil Microbial Communities and Associated Functions to Temperature and Freeze-Thaw Cycle Frequency. Environmental Microbiology, 10, 2223-2235. http://dx.doi.org/10.1111/j.1462-2920.2008.01644.x
[38]	Kay, B.D., Fukuda, M., Izuta, H. and Sheppard, M.I. (1981) The Importance of Water Migration in the Measurement of the Thermal Conductivity of Unsaturated Frozen Soils. Cold Regions Science and Technology, 5, 95-106. http://dx.doi.org/10.1016/0165-232X(81)90044-6
[39]	Lu, S., Ren, T., Gong, Y. and Horton, R. (2007) An Improved Model for Predicting Soil Thermal Conductivity from Water Content at Room Temperature. Soil Science Society of America Journal, 71, 8-14. http://dx.doi.org/10.2136/sssaj2006.0041
[40]	Nikolaev, I.V., Leong, W.H. and Rosen, M.A. (2013) Experimental Investigation of Soil Thermal Conductivity over a Wide Temperature Range. International Journal of Thermophysics, 34, 1110-1129. http://dx.doi.org/10.1007/s10765-013-1456-5
[41]	Campbell, G.S., Jungbauer Jr., J.D., Bidlake, W.R. and Hungerford, R.D. (1994) Predicting the Effect of Temperature on Soil Thermal Conductivity. Soil Science, 158, 307-313. http://dx.doi.org/10.1097/00010694-199411000-00001
[42]	Ochsner, T.E., Horton, R. and Ren, T. (2001) A New Perspective on Soil Thermal Properties. Soil Science Society of America Journal, 65, 1641-1647. http://dx.doi.org/10.2136/sssaj2001.1641
[43]	Seigo, S. (1977) Temperature Dependence of Thermal Conductivity of Frozen Soil. Research Report of Kitami Institute of Technology, 9, 111-122.