Optimal Scheduling of PEV Charging/Discharging in Microgrids with Combined Objectives ()
Received 25 February 2016; accepted 3 April 2016; published 6 April 2016

1. Introduction
In recent years, Microgrid is becoming an increasingly popular concept. It has flexibility to react grid supply variation and robustness to overcome grid disturbance due to its self-supporting capability. Usually, key components of a Microgrid include residential or commercial loads and localized Renewable Energy Sources (RESs) such as photovoltaic arrays, wind turbine, energy storage and Plug-in Electric Vehicles (PEVs). Renewable energy sources and green vehicles are critical to deal with the dependence of fossil energy as well as greenhouse gas emissions. According to the global greenhouse gas emission data published by the United States Environmental Protection Agency [1] in 2014, about 45% of greenhouse gas emission was produced by electricity production, transportation and buildings. The increasing penetration of RESs and green vehicles such as PEVs could be a potential solution to solve the environmental issues. However, there are open challenges to integrate them into Microgrids due to the intermittency of RESs and bi-directional power flow enabled by PEVs.
PV generated power depends significantly on weather conditions. For example, cloud could result in irradiance variation and introduce the intermittency of PV generated power. This will lead to power imbalance and frequency/voltage fluctuation in Microgrids. Although, battery packs of PEVs can function as energy swap systems to mitigate the above issue by charging and discharging, the approach of using PEV batteries has limitation and operational constraints. Firstly, PEV batteries have charge/discharge power limits based on the level of charging stations. PEVs might not be able to mitigate power imbalance when the power imbalance amount is greater than the PEV charge/discharge limits. Secondly, from PEV driver perspective, frequently charge and discharge might accelerate battery degradation.
A number of researchers have investigated PEV charging load modeling and optimal control in power grid. Ahourai et al. [2] study the impact of PEV charging load in a residential distribution network with various PEV penetration rates. Cao et al. [3] propose an optimal EV charging model in response to utility Time-of-Use (TOU) price regulation. Eric et al. [4] develop unidirectional charging regulation algorithms for an aggregator with 10,000 EVs to increase aggregator’s profits and reduce the impact of charging load and customer costs. Chenrui Jin et al. [5] investigate the optimal scheduling of EV charging with energy storage using combined information of day-ahead price and real-time price. Tushar et al. [6] propose EV charging scheme to reduce the effect of PV power intermittency and the cost of PV-powered charging stations. Castello et al. [7] explore the mitigation of load surge in local distribution network due to EV charging loads using a combination of PV panels and Energy Storage Systems (ESS). Three ESS control strategies are investigated and evaluated using data from a private site that has 25 solar-assisted charging stations and 4 at a public charging station. Weckx et al. [8] investigate PV inverter control to balance a three-phase distribution network. Bhattarai et al. [9] propose a two-stage control method for alleviating overvoltage problem of a PV-tied distribution grid. The centralized control prepares optimal set point for PV and EVs in a 15-minute time interval. Droop control is adopted as second stage decentralized control to regulate quick voltage fluctuation within 15-minute time interval. Gao et al. [10] presents an integrated control scheme to manage vehicle-to-grid operation in a distribution grid with wind turbine, ESS, and EV charging stations. Vehicle-to-grid power is regulated to minimize the total operating cost of the grid and provide frequency regulation.
This paper studies the optimization of PEV charging/discharging in Microgrids with PV arrays. The objective functions of the optimization algorithms are defined considering both for PEV driver benefits and Microgrid performance, including minimization of charging cost, minimization of Microgrid power deviation, and combining these two objectives. The simulation for different objective functions is performed with two optimization methods. The rest of the paper is organized as follows. Section 2 describes the modeling of the Microgrid and its components. Section 3 discusses the objective functions for the optimization of PEV charging/discharging control. Section 4 presents the optimization methods and the simulation results. Section 5 concludes the presented work.
2. Microgrid Model
Figure 1 shows the Microgrid used in this study. It consists of commercial building load, four sets of PV arrays, and three bi-directional Electric Vehicle Supply Equipment (EVSE) for PEV charging/discharge. The commercial building load is modeled as data-based load profile which demonstrates the feature of certain type of commercial building. Four PV arrays are connected to the Microgrid through solar inverters. They provide PV generation as RES in the Microgrid. Intermittency caused by cloud variation is considered in the PV array model. We assume that multiple PEVs can connect to the same EVSE at different timeslots in a day. When a PEV connects to an EVSE, it can be charged or discharged based on the grid condition and the requirement specified by
![]()
Figure 1. Microgrid topology with commercial building load, PEVs and solar generation.
the PEV driver. Meters are placed to measure power consumption of each component and breakers are designed to protect Microgrid from over-current. The weather and location information required in Microgrid model is based on Arizona Phoenix during summer time, and a unit power factor is assumed. The Microgridis modeled using Grid Lab-D [11] , a power distribution system simulation and analysis tool. PEV charging/discharging optimization algorithms are implemented in Matlab. Co-simulation is performed between Grid Lab-D and Matlab.
2.1. Commercial Building Load
The commercial building load model is a data-based load profile extracted from Commercial and Residential Hourly Load Profiles for all TMY3 Locations in the United States published by EERE [12] . We choose a small office building type which typically has one floor with floor area over 3000 ft2 [13] . Only electricity load of the building are considered in the commercial building load model. The load profile of selected commercial building is shown in Figure 2.
2.2. Photovoltaic Arrays
The solar irradiance that PV array receives can be calculated by (1)
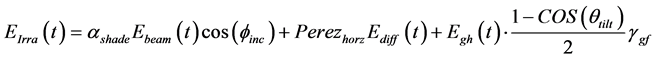 (1)
(1)
where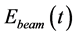 ,
,  and
and 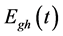 are direct normal irradiance, sky diffuse horizontal irradiance and global horizontal irradiance;
are direct normal irradiance, sky diffuse horizontal irradiance and global horizontal irradiance; 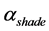 is shading factor;
is shading factor; 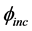 is solar incident angle;
is solar incident angle; 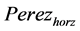 is the Perez horizon parameter that used to determine diffuse irradiance [14] ;
is the Perez horizon parameter that used to determine diffuse irradiance [14] ; 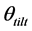 and
and 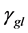 are solar module tilt angle and ground reflectivity that commonly determine ground reflected irradiance. The PV module generated power can be calculated by (2)
are solar module tilt angle and ground reflectivity that commonly determine ground reflected irradiance. The PV module generated power can be calculated by (2)
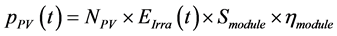 (2)
(2)
where  is number of PV arrays;
is number of PV arrays; 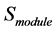 represents module area; and
represents module area; and 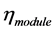 is PV module conversion efficiency.
is PV module conversion efficiency.
The simulation parameters of PV array model in Grid Lab-D are listed in Table 1. The orientation azimuth angle and panel tilt angle are set to 180˚ and 33.5˚, respectively, for maximizing received solar irradiance. The
![]()
Figure 2. Load profile of selected small office building.
![]()
Table 1. Parameters of PV array model.
efficiency of single crystal silicon PV arrays typically varies from 13% to 17%. We select the median energy conversion efficiency of 15%. The PV array area is referenced from Canadian Solar CS6P-255P Black Solar Panel. Each PV array consists of 40 CS6P-255P panels. The area of a single CS6P-255P panel is ![]() (1.61 m2).
(1.61 m2).
The variation of PV array output power due to the change of weather condition is considered in this model. The shading factor, ![]() , is designed as a random variable between 7:00 am - 11:30 am to emulate the impact of cloud shading on PV power generation in a cloudy day. The PV power output with intermittency caused by fast shading change is shown in Figure 3.
, is designed as a random variable between 7:00 am - 11:30 am to emulate the impact of cloud shading on PV power generation in a cloudy day. The PV power output with intermittency caused by fast shading change is shown in Figure 3.
2.3. PEV Charging/Discharging Model
In this Microgrid model, PEV charging stations are modeled as AC level II EVSE units with 6.6 kW maximum charging/discharging rate. The power demand/output of ![]() EVSE can be represented as
EVSE can be represented as
![]() (3)
(3)
where ![]() is the maximum power that an EVSE allows PEV to be charged or discharged.
is the maximum power that an EVSE allows PEV to be charged or discharged. ![]() is a time function of charge/discharge status and the ratio of actual and maximum charge/discharge rate,
is a time function of charge/discharge status and the ratio of actual and maximum charge/discharge rate,![]() .
.
![]() (4)
(4)
The total PEV charge/discharge power for all EVSE units can be expressed as
![]() (5)
(5)
![]()
Figure 3. The intermittent PV power output.
where, ![]() represents the number of EVSE units. The PEV charging/discharging rate of
represents the number of EVSE units. The PEV charging/discharging rate of ![]() PEV connected to
PEV connected to ![]() EVSE at time t can be expressed as
EVSE at time t can be expressed as
![]() (6)
(6)
where ![]() and
and ![]() represent the arriving and leaving time of the
represent the arriving and leaving time of the ![]() PEV connected to
PEV connected to ![]() EVSE.
EVSE.
3. Three Optimization Cases for PEV Charging/Discharging Control
3.1. Case 1: Optimal PEV Charging/Discharging Schedule to Minimize PEV Charging Cost
The objective of this optimization problem is to minimize the overall PEV charging cost in the Microgrid. Consider time period of 24 hours with time steps of![]() ,
,![]() . The object function of PEV charge/dis- charge scheduling is shown in (7).
. The object function of PEV charge/dis- charge scheduling is shown in (7).
![]() (7)
(7)
where ![]() is time interval between
is time interval between ![]() and
and![]() .
. ![]() is the total charge/discharge power of all EVSE units, which is defined in (5).
is the total charge/discharge power of all EVSE units, which is defined in (5). ![]() is the real time electricity price as shown in Figure 4. This Time of Use rate is obtained from Phoenix local utility for summer plan [15] .
is the real time electricity price as shown in Figure 4. This Time of Use rate is obtained from Phoenix local utility for summer plan [15] .
The constraints of this optimization problem are defined in (8), (9) and (10).
1) Single PEV charge and discharge rate should not exceed power limit.
![]() (8)
(8)
where ![]() and
and ![]() are absolute value of maximum charge and discharge rate,
are absolute value of maximum charge and discharge rate,![]()
![]() .
.
2) PEV battery SOC should not exceed an acceptable SOC range ![]()
![]() (9)
(9)
where ![]() represents the total capacity of PEV battery. In this study, the PEV battery specification uses Nissan leaf 2013 battery packs. The total battery capacity is set as 24 kWh.
represents the total capacity of PEV battery. In this study, the PEV battery specification uses Nissan leaf 2013 battery packs. The total battery capacity is set as 24 kWh. ![]() and
and ![]() are lower and upper SOC thresholds.
are lower and upper SOC thresholds.
3) At PEV leaving time, battery should be charged above lowest acceptable SOC, but lower than SOC upper threshold
![]() (10)
(10)
where ![]() is lowest acceptable SOC at PEV leaving time.
is lowest acceptable SOC at PEV leaving time.
3.2. Case 2: Optimal PEV Charge/Discharge Schedule to Minimize Microgrid Power Deviation
From Microgrid point of view, large deviation between the local load demand and grid supply capability is not acceptable. In some energy plan, electricity supplier will publish day-ahead load forecasting information commonly with TOU as a guild of customer power usage. The published information is not only the prediction of customer power consumption activity, but also as power supply plan in one day ahead. By following the day-ahead load signal, Micro Grid can contribute to main grid load regulation and benefit from TOU price plan.
For this optimization problem, we assume that the power supplier published day-ahead load schedule is as shown in Figure 5. To minimize power deviation, we define the objective function as a root mean square error as shown in (11)
![]() (11)
(11)
where ![]() is the commercial building power demand;
is the commercial building power demand; ![]() is total power generation of four PV arrays; and
is total power generation of four PV arrays; and ![]() is the day-ahead load forecasting.
is the day-ahead load forecasting.
3.3. Case 3: Optimal PEV Charge/Discharge Schedule with Combined Objective Functions
The objective of third optimization problem is to minimize charging cost and Microgrid power deviation simultaneously. The objective function is defined as shownin (12)
![]() (12)
(12)
where, ![]() is a tradeoff coefficient of two separate objectives. Other constraints remain the same as before.
is a tradeoff coefficient of two separate objectives. Other constraints remain the same as before.
4. Optimization Methods and Simulation Results
The optimization of PEV charging/discharging scheduling is investigated in a Microgrid described in Section 2. It is assumed that EVSE model has following information: PEV arriving time, initial SOC and vehicle leaving time. The simulation is performed with the number of PEVs and their arriving time, leaving time, and initial SOC listed in Table 2. Table 3 lists the values of SOC constraints define in (9) and (10).
4.1. Mixed Integer Linear Programming (MILP) Method for the Minimization of PEV Charge Cost
This section presents the optimization of PEV charging/discharging scheduling using MILP method. The objective function and constraints for minimizing PEV charge cost are defined in Section 3.1. For the MILP method, the objective function in (7) is modified to
![]()
Figure 5. Day-ahead load forecasting for Microgrid.
![]()
Table 2. Available PEVs in Microgrid and their arriving time, leaving time, and initial SOC.
![]()
Table 3. SOC constraints used in the simulation
![]() (13)
(13)
where ![]() minutes is the simulation time step. In MILP method, the possible PEV charge/discharge power is restricted to maximum charge/discharge power rate based on PEV charging state.
minutes is the simulation time step. In MILP method, the possible PEV charge/discharge power is restricted to maximum charge/discharge power rate based on PEV charging state. ![]() is defined to represent charging state of a PEV as shown in (14). Idling state means that the EVSE is not charging or discharging a PEV.
is defined to represent charging state of a PEV as shown in (14). Idling state means that the EVSE is not charging or discharging a PEV.
![]() (14)
(14)
Based on TOU rate in Figure 4, available PEVs in Table 2, objective function (13), and constraints in (9), (10), (14), and Table 3, the MILP algorithm finds optimal charging/discharging schedules for PEVs connected to EVSE1-EVSE3 as shown in Figures 6-8. The SOC variations for PEVs connected to EVSE1-EVSE3 are given in Figures 9-11. From these figures, we can see that the final SOCs of all the PEVs meet the charging requirement and the lowest SOC values are above the lower SOC threshold during the charging process. The time function of the accumulated charge price for individual PEVs are shown in Figures 12-14. The accumulated charge price drops when a PEV provides reverse power to the grid, such as EVSE1-PEV3, as shown in Figure 12.
Figure 15 shows the Microgrid power profile using MILP method for the optimization of PEV charging/dis- charging scheduling. The power profile includes PV generation, commercial building load, and PEV charge/ discharging power. It is seen that the power fluctuation is quite severe and frequent. At time around 19:00 pm, the power variation within 10 minutes is about 40 kW.
![]()
Figure 6. Charging/discharging schedule for PEVs connected to EVSE1.
![]()
Figure 7. Charging/discharging schedule for PEVs connected to EVSE2.
![]()
Figure 8. Charging/discharging schedule for PEVs connected to EVSE3.
![]()
Figure 9. SOC variation for PEVs connected to EVSE1.
![]()
Figure 10. SOC variation for PEVs connected to EVSE2.
![]()
Figure 11. SOC variation for PEVs connected to EVSE3.
![]()
Figure 12. Accumulated PEV charge price for PEVs connected to EVSE1.
![]()
Figure 13. Accumulated PEV charge price for PEVs connected to EVSE2.
![]()
Figure 14. Accumulated PEV charge price for PEVs connected to EVSE3.
![]()
Figure 15. Microgrid metered power using MILP method.
4.2. Nonlinear Programming Method for Minimizing Microgrid Power Deviation
The objective function to minimize the power deviation of the Microgrid has been defined in (11). Constraints of PEV charge/discharge are defined in (8), (9) and (10). Due to the nonlinear feature of the objective function, this optimization problem is solved using Nonlinear Programming technique. We assume that the TOU rate and available PEVs in Microgrid are the same as MILP method in Case 1. The simulation results obtained by Nonlinear Programming method are shown in Figures 16-25. Comparing with MILP method, the PEV charging/ discharging rate using Nonlinear Programming method can be any value between [−6.6 kW, 6.6 kW] as shown in Figure 16, Figure 19, and Figure 22. For the SOC requirement, Figure 17, Figure 20 and Figure 23 illu-
![]()
Figure 16. Charging/discharging schedule for PEVs connected to EVSE1.
![]()
Figure 17. SOC variation for PEVs connected to EVSE1.
![]()
Figure 18. Accumulated PEV charge price for PEVs connected to EVSE1.
![]()
Figure 19. Charging/discharging schedule for PEVs connected to EVSE2.
![]()
Figure 20. SOC variation for PEVs connected to EVSE2.
![]()
Figure 21. Accumulated PEV charge price for PEVs connected to EVSE2.
![]()
Figure 22. Charging/discharging schedule for PEVs connected to EVSE3.
![]()
Figure 23. SOC variation for PEVs connected to EVSE3.
![]()
Figure 24. Accumulated PEV charge price for PEVs connected to EVSE3.
![]()
Figure 25. Comparison of Microgrid metered power with day-ahead forecasted power consumption.
strate that the Nonlinear Programming method can also meet the SOC requirement defined in (9) and (10). The accumulated PEV charge price using Nonlinear Programming method are shown in Figure 18, Figure 21 and Figure 24, and the Microgrid metered power consumption is shown in Figure 25.
Table 4 compares the PEV charge bill for Case 1 and Case 2 optimization approaches. Although the total PEV charge price in Case 1 is 18.35% lower than Case 2, the Case 1 optimization approach results in large power fluctuationin Microgrid as shown in Figure 15. With the objective of minimizing power deviation, the Case 2 optimization approach can generally follow day-ahead power forecast from power suppliers as shown in Figure 25.
4.3. Optimization with Combined Objectives
The objective function for Case 3 optimization approach with combined objectives is defined in (12). To find a proper value for the weightingfactor a, two sweep testsare performed. The first sweep test selects the range of a values from 0.1 to 0.9 with a step size of 0.1. The second sweep test selects the range of a values from 0.01 to 0.09 with a step size of 0.01. The values of PEV charge bill and the Root Mean Square Error (RMSE) of power deviation in (12) are calculated for all the test points. Selected calculation results from the sweep tests are listed in Table 5. When a is between 0.01 and 0.05, the increase of a value can significantly reduce the RMSE of power deviation with reasonable increase of total charge bill. When a value is greater than 0.05, its impact to RMSE of power deviation is reduced. For this reason, we select the a value to be 0.05. With this weighting factor value, the optimized PEV charging/discharging schedules for EVSE1-EVSE3 are shown in Figures 26-28. The Microgrid metered power consumption is shown in Figure 29. Comparing to Case 1 and Case 2 optimiza- tion approaches, the total charge cost and power deviation in Case 3 are between Case 1 and Case 2 performance. This achieves the objective of balancing the control of charge cost and Microgrid power deviation.
![]()
Figure 26. Charging/discharging schedule for PEVs connected to EVSE1 in Case 3 optimization.
![]()
Figure 27. Charging/discharging schedule for PEVs connected to EVSE2 in Case 3 optimization.
![]()
Figure 28. Charging/discharging schedule for PEVs connected to EVSE3 in Case 3 optimization.
![]()
Figure 29. Microgrid metered power consumption in Case 3 optimization.
![]()
Table 4. Comparison of PEV charge bill for Case 1 and Case 2 optimization approaches. .
![]()
Table 5. Sweep test for selecting the value of weighting factor. .
5. Conclusion
In this paper, a Microgrid model has been built with commercial building load, PV array generation and bi- directional PEV charging/discharging stations. The optimization of PEV charging/discharging schedule has been studied with three different objective functions and two optimization methods. The first objective function is to minimize the PEV charging cost; the second objective function is to minimize Microgrid power deviation; and the third objective function combines the first two objective functions. The simulation results show that the optimization with combined objectives can achieve relative low charging cost with acceptable Microgrid power deviation. The simulation results also illustrate that the charging/discharging of PEVs provides grid service to reduce the intermittency of PV power generation. In future study, we will focus on decentralied PEV charging/ discharging control for a PEV fleet in larger scale smart grid with renewable energy sources.