“Hot Nano Spots” as an Interpretation of So-Called Non-Thermal Biological Mobile Phone Effects ()
Received 15 February 2016; accepted 27 March 2016; published 30 March 2016

1. Introduction
Mobile phones may cause eventual non-specific biological effects which usually are classified as being of implausible non-thermal nature. This is expressed by several review papers (e.g. [1] - [6] ) that are based on a very high number of experimental and theoretical investigations. Quantum theory speaks against these effects due to the low quantum energy of mobile phone radiation, continuum theory due to very low values of global temperature increase. In fact, a generally accepted interpretation is missing. The above mentioned reviews accept non- thermal effects, at least in principal ways. On the other hand, the reference [7] comes to the conclusion that they are a myth and “that non-thermal microwave effects simply do not exist”. With respect to mobile phones, this is also supported by the present text, provided that we interpret the term “thermal” in an extended way.
In the early state of discussion, the biological risks through microwave radiation were estimated on the basis of total energy as being absorbed by the human body, not considering that a biological system―e.g. the human head―tends to show a very heterogeneous structure. However, practically all more recent work is focused on the specific absorption rate (local SAR in W/kg). Considering the dielectric properties of the different types of tissues (such as skin, skull and brain), numerical modeling―or also experimental phantom testing―of the multi-layered head is applied to identify “hot spots” of maximum SAR. As a problem, the results depend on the ratio of the wave length and the geometry of the different layers, due to reflection effects and specific absorption rates. In recent studies, this was met by parameter variation in order to identify the worst case [8] .
SAR values were determined with spatial resolutions down to the order of 1 mm (e.g. [9] ). But even this strategy yields rise-of-temperature levels θ that do not exceed the order of 1 K which is not likely to explain significant biological after-effects. In order to identify potential key mechanisms for so far unclarified effects, we should leave the level of millimeters and search at even lower ones. As well known, the thickness of cellular membranes is slightly above 5 nm. For this level, reference [10] describes specific changes of electric field conditions. However, even more pronounced effects can be expected for the molecular level round a nanometer. This is indicated by studies on heterogeneous matter as industrially treated by microwaves (e.g. [11] - [14] ). The corresponding effects are not considered as a threat, but as an advantageous measure, mainly to attain selective heating of heterogeneously distributed substances. The involved field intensities are not likely to arise in the context of mobile phones. However, the involved physical mechanisms can be assumed to be valid in a general way, i.e. also for living matter which is highly heterogeneous on the level of nanometers.
In the following, we consider a sub-region within an a priori over-heated hot spot, considering this region as a heterogeneously built up cellular volume that contains portions of biologically functional molecules. The corresponding “thermal” effects are estimated by the well known classical theory of polarization. This offers a con- ventional explanation for all three the possible existence of single unexpected effects, their low reproducibility and their low intensity. The basis of this explanation is given by the assumption that hot spots contain even hotter “nano spots”, on a molecular level due to g-relaxation effects. At first time, the basic idea was presented in reference [15] . Here, the concept is put for discussion in a closer way.
2. Preconditions
The fact that even “hot spots” tend to exhibit rather low levels of temperature increase θ results among others from the considerably large difference between the mobile phone (MP) frequency fMP (order 1 - 2 GHz) and the water molecule’s so-called g-relaxation frequency
 (1)
(1)
with F a factor that considers deviations from spherical molecule shape, among others. This well known Debye formula considers polar molecules in the most approximate way. According to it, fR increases with increasing thermal energy kT which however can be assumed to be constant for the living system. It decreases with the viscosity h which results from the surrounding of the considered molecule and which can been interpreted as a source of inner friction of the medium. For the following considerations, a significant parameter is the molecule size d. For water molecules (WM) it is about 0.2 nm which yields fR,WM close to 10 GHz, with variations due to the varying content of bound water (clusters, hydration etc.) that yields increased effective h.
The water content of biological tissues is well reflected by the value of the permittivity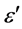 , the real part of the complex value
, the real part of the complex value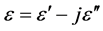 . Figure 1 shows a frequency response of
. Figure 1 shows a frequency response of  as being typical for tissues like muscle, brain or blood. Cellular liquids existing of 100% free water would yield
as being typical for tissues like muscle, brain or blood. Cellular liquids existing of 100% free water would yield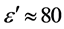 , and this value would be constant for frequency values below 1 GHz (until starting ß-dispersion due to membrane structure charging). On the other hand, Figure 1 shows a slight but continuous increase of
, and this value would be constant for frequency values below 1 GHz (until starting ß-dispersion due to membrane structure charging). On the other hand, Figure 1 shows a slight but continuous increase of  with decreasing f. This indicates that larger molecular structures get into relaxation resonance in a distributed way. The latter results from the fact that 1) a large molecular variety is given and that 2) even a well defined type of molecule of constant d will show distributed fR due to variations of h according to the neighboring molecular structures.
with decreasing f. This indicates that larger molecular structures get into relaxation resonance in a distributed way. The latter results from the fact that 1) a large molecular variety is given and that 2) even a well defined type of molecule of constant d will show distributed fR due to variations of h according to the neighboring molecular structures.
According to well known theory, microwave radiation acting on a quasi-homogeneous polar medium can be assumed to cause a dielectric energy loss density
![]()
Figure 1. Frequency response of the real part e' of permittivity as being typical for biological tissues.
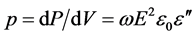 (2)
(2)
with the energy loss P, the angular frequency ω = 2πf, the electric field E and the vacuum permittivity ε0. For a given frequency, the permittivity 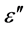 is a linear measure for the contribution of a given type of molecule to dielectric losses, thus representing a key quantity for the following discussion. For a volume that contains a single type of polar molecules, it is given by
is a linear measure for the contribution of a given type of molecule to dielectric losses, thus representing a key quantity for the following discussion. For a volume that contains a single type of polar molecules, it is given by
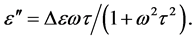 (3)
(3)
Here Δε expresses the total decrease of 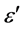 as arising in the considered relaxation frequency range (of more than two orders of magnitude width) due to vanishing orientation polarization. The quantity Δε increases with increasing polar moment and-for a given moment-it decreases with increasing size d of the considered type of molecule (or moveable molecular fragment). A quantity which is of special interest for the following discussion
as arising in the considered relaxation frequency range (of more than two orders of magnitude width) due to vanishing orientation polarization. The quantity Δε increases with increasing polar moment and-for a given moment-it decreases with increasing size d of the considered type of molecule (or moveable molecular fragment). A quantity which is of special interest for the following discussion
is the relaxation time constant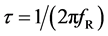 . From (1), it increases strongly with increasing size d, significantly
. From (1), it increases strongly with increasing size d, significantly
depending on the molecular shape. For water molecules surrounded again by water molecules, the already mentioned frequency value fR,WM = 10 GHz yields a value of τ close to 100 ps. According to (3), the frequency dependence of 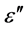 shows Gaussian shape, a maximum arising for f = fR, also corresponding with maximum losses.
shows Gaussian shape, a maximum arising for f = fR, also corresponding with maximum losses.
3. Description of Model
As representative for a local region of the considered biological system, let us consider a volume 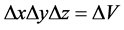 as schematically sketched in Figure 2. In order to enable the application of continuum theory, let us assume that ΔV contains a considerably high number of molecules, corresponding to the dimension of at least some nanometers. It should be noted that an analogous assumption was made in [11] , however, for larger, micro-meter sized regimes.
as schematically sketched in Figure 2. In order to enable the application of continuum theory, let us assume that ΔV contains a considerably high number of molecules, corresponding to the dimension of at least some nanometers. It should be noted that an analogous assumption was made in [11] , however, for larger, micro-meter sized regimes.
For a systematic discussion, we assume the following three types of molecular functions:
a) A predominant volume fraction cWM of polar (cellular) water molecules (WM),
b) A small fraction cFM of larger polar functional molecules (FM), or mobile polar molecular fragments, respectively, and
c) A small fraction cPM of large protein molecules (PM), or other macro-molecules, respectively, which may be polar as an option.
For a rough modelling of the heterogeneous case of water including a single type of polar particles FM, just two contributions to polarization are given. Neglecting intermolecular interactions, linear superposition yields
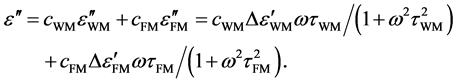 (4)
(4)
![]()
Figure 2. Considered volume ΔV containing a representative amount of molecules of type WM, FM and PM.
Figure 3 shows the two terms, related to the maximum value ![]() (fR,WM) for water. A 20% volume content―i.e. cFM = 0.2―is assumed for a molecular component FM of about tenfold volume, after (1) corresponding to a relaxation frequency fR,FM close to 1 GHz. For most simple conditions, let us assume balanced polar behaviour of the two components according to
(fR,WM) for water. A 20% volume content―i.e. cFM = 0.2―is assumed for a molecular component FM of about tenfold volume, after (1) corresponding to a relaxation frequency fR,FM close to 1 GHz. For most simple conditions, let us assume balanced polar behaviour of the two components according to![]() , as given in Figure 3. Finally, 10% non-polar molecules of type PM are assumed, corresponding to cPM = 0.1 and cWM = 0.7.
, as given in Figure 3. Finally, 10% non-polar molecules of type PM are assumed, corresponding to cPM = 0.1 and cWM = 0.7.
Interpreting continuum theory in a depictive way, irradiation of the above system can be expected to yield the following tendencies as a function of frequency:
A) Low frequency, e.g. f = 1 MHz, i.e. well below the MP frequency range
Both WM and FM are “operated” below fR. Due to their relatively small size d, they will follow the dynamic changes of the electric field vector E without significant delay, i.e. the polar moment will show some orientation. The extent of orientation will be equivalent to the high value ![]() but in fact will still be extremely small due to the high absolute temperature which favors chaotic orientations of the polar moments. In spite of unlimited molecular rotation below fR, the orientation will increase the a priori strong Brownian motion in a negligible way only, since the additional relative surface velocity of the molecule is small due to both small f and small d.
but in fact will still be extremely small due to the high absolute temperature which favors chaotic orientations of the polar moments. In spite of unlimited molecular rotation below fR, the orientation will increase the a priori strong Brownian motion in a negligible way only, since the additional relative surface velocity of the molecule is small due to both small f and small d.
B) High frequency e.g. f = 10 GHz, i.e. above the MP frequency range
According to f = fR, WM, maximum ![]() is given here for water. This means that the orientation is restricted but―contrary to A―causing a considerably high rotational vibration-as schematically indicated in Figure 4(a)- corresponding to optimum dielectric heating. Taking advantage of the Brownian motion concept in a reverse way, the corresponding increase of local temperature can be interpreted by effective friction processes due to high rotational surface velocity. The large molecule type FM is operated above fR due to high d. It will not follow the dynamic changes of E thus not showing energy uptake through the mechanism of rotational orientation. In fact, an ensemble of such molecules will show a local minimum of thermal energy, restricted through energy uptake from the surrounding water matrix. However, with the assumption of the high water content (70%), the volume ΔV can be assumed to show quasi-homogeneous thermal conditions with small deviations from global θ.
is given here for water. This means that the orientation is restricted but―contrary to A―causing a considerably high rotational vibration-as schematically indicated in Figure 4(a)- corresponding to optimum dielectric heating. Taking advantage of the Brownian motion concept in a reverse way, the corresponding increase of local temperature can be interpreted by effective friction processes due to high rotational surface velocity. The large molecule type FM is operated above fR due to high d. It will not follow the dynamic changes of E thus not showing energy uptake through the mechanism of rotational orientation. In fact, an ensemble of such molecules will show a local minimum of thermal energy, restricted through energy uptake from the surrounding water matrix. However, with the assumption of the high water content (70%), the volume ΔV can be assumed to show quasi-homogeneous thermal conditions with small deviations from global θ.
C) Medium frequency e.g. f = 1 GHz, i.e. corresponding to the mobile phone frequency range
Here, water molecules are operated below relaxation frequency, corresponding to strongly restricted power dissipation. As well, the latter is valid for the large molecule type PM which―if being polar―is operated above relaxation frequency. On the other hand, since f is close to fFM, optimum excitation results for the functional type of molecules. As a consequence of dynamic rotational vibration, changed interaction can be expected with neighbouring molecules, such as indicated in Figure 4(b). And finally, locally concentrated friction with surrounding molecules of arbitrary type will yield a local maximum of loss, equivalent to a hot “nano spot” (HNS) since restricted to a sub-region of about 1 nm size. The degree of the excess local temperature DTHNS will be restricted through the cooler surrounding, a tendency which increases with decreasing cFM. But still, within the hot spot of millimeter size, we can expect even hotter nano spots which are practically not detected by SAR calculation or by thermal measurements (e.g. within multi-layered phantoms) due to restricted resolution of these methods.
Beyond the above qualitative discussion, a quantitative estimation can be based on the responses of ![]() as given in Figure 3 for the above defined system. First, let us assume a mobile phone radiation frequency fMP close to 1 GHz. That is, accidentally it would coincide with the relaxation frequency of the functional molecule type FM according to fMP = fR,FM. In this case, Figure 3 yields for the two contributions to
as given in Figure 3 for the above defined system. First, let us assume a mobile phone radiation frequency fMP close to 1 GHz. That is, accidentally it would coincide with the relaxation frequency of the functional molecule type FM according to fMP = fR,FM. In this case, Figure 3 yields for the two contributions to ![]() the ratio
the ratio
![]()
Figure 3. Contribution of water molecules and functional molecules, respectively, to the imaginary part ![]() of permittivity as a function of frequency f and as resulting from (3) for the considered composition of volume element ΔV. Notice: the data is related to
of permittivity as a function of frequency f and as resulting from (3) for the considered composition of volume element ΔV. Notice: the data is related to![]() , i.e. the maximum value for pure water.
, i.e. the maximum value for pure water.
![]()
![]() (a) (b)
(a) (b)
Figure 4. Illustration of rotational vibrations of molecules (dotted). (a) For 10 GHz, i.e. optimum excitation of water molecules, yielding a quasi-homogeneous temperature increase due to the high content of water. (b) For 1 GHz as being relevant for mobile phones, the excitation being restricted to functional molecules that happen to fulfill the condition fMP = fR,FM, the local phenomenon being equivalent to a hot nano spot.
![]() (5)
(5)
corresponding to portions of 59% and 41% to total losses. This means that FM contributes to the global energy increase of the volume ΔV in a predominant way, in spite of its small volume portion of only 20%. Neglecting active energy dissipation, the resulting values θFM and θWM of local temperature increase (on a molecular level) depend on the individual values of density ρFM , ρWM and specific heat κFM, κWM. Their relationship follows from the above ratio according to
![]() (6)
(6)
Neglecting differences of ρ and also of κ would yield a temperature ratio
![]() (7)
(7)
i.e. a 5-fold overheat of FM compared to WM. And finally with this proportion we find from the total energy
![]() (8)
(8)
the ratio
![]() (9)
(9)
It means that compared to the global temperature increase―as being detectable by measurement―, the protein portion within the considered volume is locally characterized by 3-fold temperature increase. This ratio quantity r3 expresses in an effective way the “excess rate” of temperature which can be expected to determine the chemical and biological behaviour of the considered functional type of molecule, thus representing a characteristic of the resulting hot nano spot.
The above estimation concerns 1 GHz. For higher fMP, e.g. close to 2 GHz, the energy uptake by WM would be higher due to reduced distance from fR,WM = 10 GHz. On the other hand, the uptake by FM will be slightly decreased since not operated any longer at relaxation frequency. As a consequence, all three ratio terms r1, r2 and r3 would be reduced. However, it should be stressed that all above data is based on the assumption that the rather high portion of 20% FM is given within the considered volume. Smaller concentrations―which are more likely to exist in practice―yield increased ratio terms r2 and r3. Roughly, a reciprocal dependence can be assumed corresponding to maximum values of temperature increase for singular functional molecules which happen to show relaxation at the frequency of mobile phones.
4. Possible Consequences of Nano Hot Spots
Let us now discuss the possible consequences of hot nano spots. The above model indicates that the functional behavior of the affected molecules will not correspond to the state of “hot spot” temperature increase―e.g. θHS = 1 K―, but to the state of a higher “hot nano spot” (HNS) temperature increase. For the example of data set for (9), this results in the value
![]() (10)
(10)
In analogous ways, the above way of modelling is consistent with interpretations in [11] [12] where the term “spatial hot spot” is introduced. With restrictions, the molecular behavior of the nano spot as resulting from the above assumed microwave radiation of globally 1 K will be equivalent to that which would result from global heating of 3-fold intensity through conventional non-microwave heating (e.g. the physiological thermal regulation of the organism). This concerns all micro-chemical and micro-physical functions of the affected molecules and the resulting global biomedical consequences on metabolism or on the neural system. Examples are the following:
a) Structural functions-molecular structures becoming less stable (see e.g. [16] for membranes) and more susceptive to destabilizing influences like changes of pH or ionizing radiation.
b) Enzymatic tasks-the molecular interaction becoming less stable thus reducing the probability of enzymatic effectiveness.
c) Controlling functions at membrane channels-affected polar molecules yielding increased or decreased permittivity, 1) to ions as a basis of neural effects as schematically outlined in Figure 5 (after reference [15] ), or 2) to metabolic products as a basis of growth effects, as repeatedly reported in literature.
According to literature, it cannot be excluded that very specific effects are beyond the here proposed concept of nano spots. As a corresponding “archetype of (true) non-thermal microwave effects”, reference [4] considers
![]()
Figure 5. Schematic outline of possible effects on a voltage-gated membrane channel of a neuron membrane. In state I, the polar end of the gate protein is directed upwards through the static electric membrane field E, thus preventing diffusion of ions into the cell. Microwave radiation may yield vibrations of the polar end, thus reducing its stability with respect to a field reduction through a depolarizing, exciting field Ed. As a consequence, it may favour the protein ends transfer into the more stable state II (thin lines) corresponding to channel opening.
the recombination of radical pairs through magnetic field components. However, such effects need very high field intensities (exceeding 0.1 T [15] ), as never been involved in the context of mobile phones.
Here it should be stressed that all above listed effects (a) to (c) can be assumed to be weak with respect to quantitative consequences. First of all, the probability is small that a given type of functional molecule happens to fulfill the condition fMP = fR,FM for full resonance. But even if it does, considering the role of h, an ensemble of a given type of molecule will not show a sharp resonance, but fR,FM of the individual molecules will be of distributed nature as depending on many parameters. Thus the maximum effects of a given value fMP will concern a restricted portion of individuals. And inside a hot spot, the concentration and temperature of hotter nano-spots will vary as well. Especially, an absolute energy maximum will be restricted to the center of an ensemble of identical molecules of type FM. The resulting statistical energy distribution can again serve as an explanation for the finding that mobile phone effects show weak intensity and low reproducibility, if occurring at all.
According to the above, the model presented in this paper indicates that a variety?if not the total-of apparently non-thermal effects can be interpreted as actually being of thermal nature. But it also indicates that such effects exhibit very low probability and are not likely to cause significant consequences on health, even for long-term activity.
Finally, it should be mentioned that the above concept promises to favor interdisciplinary discussions of health risks due to its consistent “thermal” nature. The concept distinguishes thermal effects on the following three levels:
a) The global level of total organism on the rough geometric scale of a meter.
b) The level of a cranial “hot spot” on the scale of millimeters, as taken as a basis for the determination of SAR values.
c) The level of molecular “nano hot spots” on the scale of nanometers.
At present, the SAR value according to level b) is indicated as a measure for risks in a global way, i.e. irrespective of frequency. On the other hand, it is evident, that molecular effects depend on the considered frequency band of radiation. Further studies should establish comparative assessments for the individual bands, in order to characterize the individual proneness to effects of molecular type c) through a second parameter. This does not necessarily need further experimental work, but can be based on systematic evaluations of the very high amount of already existing data.
5. Conclusions
Rather simple theoretical considerations that are based on conventional models of polarization yield the following main conclusions:
1) The usual SAR concept lacks from the fact that “hot spots” are defined as rather large regions with millimeter dimensions.
2) It is likely that such a region contains molecules which happen to show g-relaxation at mobile phone frequencies, thus representing considerably hotter “nano spots” which are not detected by the restricted resolution of SAR calculations or thermal measurements, respectively.
3) A given SAR-based microwave heating rate will affect such molecules more intensively than the same rate produced by non-microwave heating. The functional molecular behavior will correspond to the excess, “local” nano spot energy.
4) The hot nano spot will show thermal interaction with its cooler surrounding, analogous to the interaction of a hot spot with its even more cool surrounding, however, at a smaller (molecular) level.
5) The mechanism means that most so-called non-thermal effects―if not all―are of thermal nature in fact. The insignificant extent of effects is due to randomly distributed constellations that yield a hot nano spot.
6) A consistent interpretation of effects as thermal ones promises to favor interdisciplinary discussions of risks.
7) The estimation of risk through a mere, single SAR value is not satisfactory. A second parameter may express the proneness to possible molecular effects, depending on the given band of frequency.
Acknowledgements
The author thanks Prof. Eugenijus Kaniusas (TU Wien, Vienna, Austria) for valuable discussions and suggestions.