Problems with Translational Invariance of Three-Particle Systems

Algirdas [e-mail]

Department of Applied Informatics, Vytautas Magnus University, Kaunas, Lithuania.

DOI: 10.4236/jmp.2016.73029                

Abstract

A new method for calculation of non-relativistic energy spectrum of Coulomb three-body systems with two identical particles has been developed. The novelty of the method is the introduction of an expansion of the wave function on harmonic oscillator (HO) functions with different sizes in the Jacobi coordinates instead of only one unique size parameter in the traditional approach. The method presented obeys the principles of antisymmetry and translational invariance. The theoretical formulation has been illustrated by evaluation of ground state energies of a number of Coulomb three-body systems with two identical particles for zero HO excitation energy. The analytical solution of this problem in case of only one size parameter has been derived. The obtained results show significant advantage of the base with different sizes over the traditional approach for investigation of the bound state problem of quantum systems.

Keywords

Harmonic Oscillator Basis, Binding Energy, Variational Method, Quantum Systems with Coulomb Potential

Received 6 January 2016; accepted 14 February 2016; published 17 February 2016

1. Introduction

The paper is organized in the following way. In Section 2 we present the basic equations of our formalism which lead to the compact expression for the intrinsic Hamiltonian matrix elements of the problem. In Section 3 we calculate the ground state energies of Coulomb three-body systems with two identical particles for zero HO excitation energy. The energies are compared to the values obtained in the traditional approach, when available. Section 4 is devoted for conclusions.

2. Coulomb Three-Body Systems with Two Identical Particles

The Hamiltonian of three-particle system, with masses 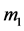and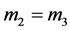, and charges equal 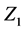and 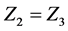interacting with Coulomb potential in laboratory reference frame can be written as sum of single-particle and two-particle operators

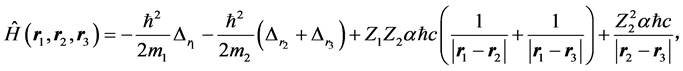(2.1)

where α is fine structure constant, and 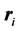the i-th particle radius vector. Let us assume that two (of the three) particles are identical. In order to get attractive interaction, one of the particles must be positive and the two others negative, or vice-versa. The two identical particles obviously have the equal masses. Therefore, it may be introduced the convenient Jacobi coordinates that not depend on the masses:

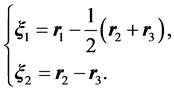(2.2)

The reduced masses that correspond to the introduced Jacobi coordinates are defined by

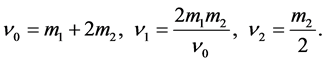(2.3)

The denominators of the expressions of the Coulomb interactions between the first and two identical particles in the Jacobi coordinates acquire the form:

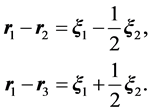(2.4)

So, the intrinsic Hamiltonian of the considered three-particle system in the Jacobi coordinates will be

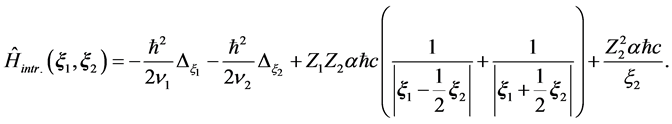(2.5)

Since the identity of two particles the mean values of two terms in the intrinsic Hamiltonian corresponding to the Coulomb interactions between the first and two identical particles are equal. Therefore the intrinsic Hamiltonian may be replaced by the equivalent one with only one doubled term of interaction:

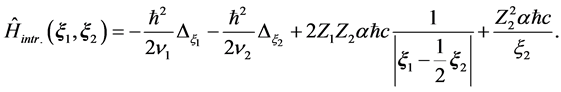(2.6)

In this paper, we introduce different sizes in the Jacobi coordinates instead of only one unique size parameter in the traditional approach. Therefore, in our method the standard procedure of transformation to dimensionless Jacobi coordinates takes the form:

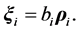(2.7)

Here 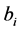are the dimensionless harmonic oscillator length parameters, one for each Jacobi coordinate (indicated with index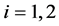) that implies a unique size for HO functions

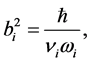(2.8)

where are the parameters with dimension of angular frequency and is the index of the reduced masses (2.3). The matrix of the intrinsic Hamiltonian will be calculated with the basis functions constructed of single-particle HO functions depending on the dimensionless Jacobi coordinates. In these coordinates the mean values of the kinetic energy terms of intrinsic Hamiltonian coincide with the mean values of the corresponding kinetic energy terms of single-particle HO Hamiltonian

(2.9)

The eigenfunctions of this Hamiltonian are orthogonal and normalized radial harmonic-oscillator wave functions that in dimensionless Jacobi coordinates have the form

(2.10)

here the quantum numbers for dimensionless Jacobi coordinates are displayed: is the number of harmonic oscillator quanta; is the principal oscillator quantum number; is the orbital angular momenta; is the Laguerre polynomial, and is the gamma function [14] . The intrinsic Hamiltonian in the dimensionless Jacobi coordinates takes the form

(2.11)

Let us rewrite the intrinsic Hamiltonian (2.11) in terms of dimensionless energy quantities. The greatest simplification may be achieved by introducing energy units. In this case, two new variational parameters are

(2.12)

These new variational parameters will replace the following ratios in the dimensionless expression of the intrinsic Hamiltonian

(2.13)

and

(2.14)

here.

Further simplification of the expression of dimensionless intrinsic Hamiltonian may be achieved taking use of the expression

. (2.15)

Finally, the dimensionless intrinsic Hamiltonian takes the form

(2.16)

Here, no assumptions are made that some parts of the Hamiltonian are negligible in comparison to others. It should be noted, that since the product is the constant, the mean values of the intrinsic Hamiltonian (2.11) and dimensionless intrinsic Hamiltonian (2.16) will have variational minimum at the same values of the variational parameters and.

The matrix of the obtained intrinsic Hamiltonian is calculated on the bound angular moment harmonic oscillator functions that can be expressed in terms of the first particle and two identical particle functions utilizing the angular momentum Clebsch-Gordan coefficients

(2.17)

here, and are total angular moment a quantum numbers of the states of the first particle, two identical particles and the three-particle system correspondingly; m is the magnetic quantum number of corresponding angular momentum; is spin variables of the i-th particle. Vector coupling of angular moment a is denoted by. The function depending on the first Jacobi coordinate is composed of angular momentum and spin functions

(2.18)

where is a spherical harmonic, is a spin-1/2 function in the spin space, is the spin quantum number of the first particle, and are the magnetic quantum numbers of orbital momentum and spin for the dimensionless Jacobi coordinate (associated with the first particle). The same self- explanatory structure have the wave function depending on the second Jacobi coordinate:

(2.19)

here and we use the simplified notation for the number of HO quanta and orbital angular moment a quantum numbers, i.e.. The spin function of two identical particles have the form

(2.20)

Let us denote the introduced vector coupled basis functions of three-particle system by ket vector

(2.21)

Let us list the conditions that should be imposed on the quantum numbers in these functions. At first, the wave functions (2.21) should be antisymmetric under permutation of two identical fermions. This imposes the well-known condition: should be an even number. At second, the total spin of the two identical particles with spin of 1/2 could take on only two values:. At third, the total angular momentum, is conserved, so its quantum numbers may take on only the integer values within the range:. Finally, the parity conservation imposes the condition:, here is the total parity of the three- particle wave function (the same for bra and ket functions in the Hamiltonian matrix element). As is usually accepted, the is related to the maximum number of total excitation oscillator quanta by formula.

The expectation values of kinetic energy operators of Hamiltonian (2.16) after application of the Wigner- Eckart theorem, may be expressed by reduced matrix element

(2.22)

represented as double-bar matrix element. The Clebsh-Gordan coefficient in this expression is Kronecker symbol for total angular momentum and its magnetic quantum numbers of the basis. The reduced matrix element of operator acting only on coordinates of first particle may be expressed in terms of 6j coefficient and the reduced matrix element between the single-particle functions depending only on coordinates of the first particle [15]

(2.23)

Since the considered Hamiltonian is a scalar in angular-momentum space, the tensorial rank of the kinetic energy operator is zero. After application of Equation (2.23), the expression of the reduced matrix element of the first kinetic energy term takes the form

(2.24)

Due to zero value of one of the parameters of the 6j coefficient, it may be significantly simplified [14] , therefore, the matrix element of the first kinetic energy term may be written as

(2.25)

Applying the same formula (2.23) for orbital momentum we may further simplify the reduced matrix element

(2.26)

After returning from the reduced to the ordinary matrix element

(2.27)

the matrix element of the first kinetic energy term assumes the form

(2.28)

The matrix element of the first kinetic energy operator in the HO basis depending on the coordinate:

(2.29)

The second kinetic energy term of Hamiltonian (2.16) may be evaluated similar way using the formula that expresses the reduced matrix element of operator acting only on coordinates of two identical particles of the three-particle coupled state in terms of 6j coefficient and the reduced matrix element between the single-particle functions depending only on coordinate [15] . Then for the matrix element of the second kinetic energy term, between the coupled three-particle harmonic oscillator functions, we find that

(2.30)

The single-particle Coulomb term as well as the second kinetic energy term of the Hamiltonian (2.16) depends on the same Jacobi coordinate, so its angular part will be calculated analogously. Then for the matrix element of the single-particle Coulomb term, between the coupled three-particle harmonic oscillator functions

(2.31)

The matrix element of the two-particle Coulomb term assumes the form

(2.32)

We calculate this matrix element by means of Talmi-Moshinsky brackets. In order to apply the Talmi- Moshinsky the moments of the coupled three-particle harmonic oscillator functions should be recoupled in the following form [15]

(2.33)

So, the reduced matrix element of the two-particle Coulomb term actually becomes the expansion in terms of the transformation matrices and reduced matrix elements with new momentum coupling scheme

(2.34)

The reduced matrix element of the two-particle Coulomb term on the functions with new coupling scheme may be further simplified

(2.35)

The expectation value of the two-particle Coulomb operator from Equation (2.16) can be obtained by expressing them in a single-particle form. This may be accomplished by means of new Jacobi coordinates. The orthogonal transformation to that Jacobi coordinates is

(2.36)

The same transformation to Jacobi coordinates should be accomplished for the wave functions. By means of Talmi-Moshinsky brackets the two particle harmonic oscillator functions may be expanded in terms of vector coupled products of the single Jacobi variable functions [16]

(2.37)

here and are oscillator quanta and angular momentum quantum numbers, associated with the center- of-mass motion, and are corresponding quantum numbers of relative motion. The Jacobi coordinate with the zero index is proportional to the center-of-mass coordinate, and Jacobi coordinate with the index equal to one is proportional to their relative coordinate. The various quantum numbers appearing in the Talmi- Moshinsky brackets are constrained by triangular inequalities, by parity conservation and by conservation of the number of quanta. The two-particle Coulomb operator will depend only on the one variable in the new basis if the parameter d of the Talmi-Moshinsky brackets takes the form

(2.38)

Then, in the denominator of the two-particle Coulomb operator may be expressed

(2.39)

here we introduce for brevity the factor C which is defined

(2.40)

Thus for the reduced matrix element of the two-particle term of the Hamiltonian (2.16) one obtains

(2.41)

The reduced matrix element in Equation (2.41) may be simplified similarly as the kinetic energy terms

(2.42)

here the radial harmonic-oscillator wave functions have the same form (2.10) and the integral may be obtained most easily by direct numerical integration. Then for the reduced matrix element of the two-particle Coulomb term, between the functions with coupled orbital angular momenta

(2.43)

Finally, the matrix element of the two-particle Coulomb term between the initial coupled three-particle harmonic oscillator functions takes the form

(2.44)

here, the summation parameters are under restrictions:

;;;

m_j―may take any allowed value for given j;; and are even numbers; (takes only two values); and;. In the expansion (2.44), we always consider all the basis states (2.37) with a number of quanta less or equal to a given number. This is the well-known prescription for HO bases to treat correctly the Pauli principle.

3. Ground State Energies Evaluation

A new method for calculation of non-relativistic energy spectrum of Coulomb three-body systems with two identical particles has been applied for calculation of ground state energies in zeroth order approach (with zero HO excitation energy). In this case, the Hamiltonian matrix has only one matrix element, therefore the application of variation principle for ground state energies calculations is significantly simplified. The traditional approach based on HO basis considers that the harmonic oscillator wave function have the same size (or the same scale) in all Jacobi coordinates. The proposed approach transforms to the traditional one with the simple substitution. In this case, the zeroth order matrix element of the dimensionless intrinsic Hamiltonian (2.16) takes the form

(3.1)

The minimization of this function may give an analytical expression for variable parameter, which is chosen to minimize the zeroth order ground-state eigenvalue

. (3.2)

So, for one variable parameter the considered variation eigenvalue problem could be solved analytically, that significantly simplify the analysis of bound state problem. The dependence of the zeroth order ground-state eigenvalue (with one variable parameter) of the dimensionless intrinsic Hamiltonian on the mass ratio of the particles and charge of the non-identical particle is illustrated in Figure 1.

Figure 1 shows that the ground-state eigenvalues have pronounced minima at some values of mass ratio. As charge of the non-identical particle increases, these ground-state eigenvalues lay lover. However, at large values of mass ratio of three-body Coulomb systems with two identical particles their binding energies calculated within the framework of the traditional approach become positive. Figure 1 displays calculation results only for electrons as identical particles, however the dependences of binding energies for other sort of identical particles with the same mass ratio will differ only with scaling factor. Therefore, the result that the binding energy of considered systems calculated within the framework of the traditional approach becomes positive at large values of mass ratio is quite general one. This is in strict contradiction to the well-established result that all Coulomb three-body systems consisting of two identical particles have at least one stable bound state against dissociation [17] . Some characteristic of the obtained dependencies of the zeroth order ground-state eigenvalues calculated within the framework of the traditional approach for the specified charges (with) are presented in Table 1. The first column tabulates the values of mass ratio up to which there exists at least one bound state for the considered three-body systems. In the following two rows the minima of the zeroth order ground-state eigenvalues are given as a function of the mass ratio. The last column contain the limit of the minima of the zeroth order ground-state eigenvalues when. Thus, for we have the “atomic” limit consisting of two light identical particles and a heavy one, on the other hand, for there is the “molecular” limit consisting of two identical heavy particles and a light one. So, the mass ratio represents the degree of adiabaticity of the considered system. The dependence of the zeroth order ground-state eigenvalue of the Hamiltonian (3.1) on the mass relation of the particles, charge of the non-identical particle, and the parameter chosen to minimize the ground-state eigenvalue is presented in Table 1.

Figure 1. The dependence of the zeroth order ground-state eigenvalue (in eV) of the Hamiltonian (3.1) on the mass ratio m₂/m₁ of the particles and charge Z₁ of the non-identical particle when identical particles are electrons. The parameter γ_min is chosen to minimize the ground-state eigenvalue. Every curve is labelled by their Z₁ value and scaled by corresponding factors: 1 (Z₁ = 1), 5.3 (Z₁ = 2), 10.8 (Z₁ = 3), and 16 (Z₁ = 4).

Table 1. The characteristics of dependence of the zeroth order ground-state eigenvalue (with one variable parameter γ) on mass ratio m₂/m₁ and charge Z₁ of the non-identical particle when the charge of any of the identical particles is Z₂ = −1. (m₂/m₁)_max is the upper mass ratio limit for which there exists at least the one bound state of the Coulomb three-body systems with two identical particles (electrons) in zeroth order approach; E_min is the minimum of the zeroth order ground-state eigenvalue at specified value of mass ratio m₂/m₁; the last column displays the limit of the zeroth order ground-state eigenvalue for infinitely small mass m₂ or infinitely large mass m₁.

It should be noted that the results presented in Table 1 remain unchanged if the signs of charges Z₁ and Z₂ are reversed.

In the presented method the minimization must be done in a two dimensional space (γ₁ and γ₂). To search the minimum of the matrix element of Hamiltonian (2.16) for zero excitation HO energy, we apply our modified Golden section search method [18] alternatively for parameters γ₁ and γ₂. This method is well-known of its stability and is fast enough in this case of one minimised function (computation time takes about few seconds). For the bound states, the parameters γ₁ and γ₂ are calculated by minimization of the corresponding zeroth ground- state eigenvalue of the Hamiltonian (2.17). Aiming to demonstrate the possibilities of our method, we have calculated the zero order binding energies for a large set of three-body Coulomb systems with two identical particles. These results are presented in Table 2.

Table 2. The non-relativistic binding (total) energies (in eV) for the ground-states of Coulomb systems with two identical particles. Energies are for values of parameters γ, γ₁ and γ₂, which give the lowest energy for zero excitation HO energy. The “exact” numerical binding energies of ground-states are also indicated.

4. Conclusions

In this paper the new HO basis expansion method for calculation of non-relativistic energy spectrum of three- body systems with two identical particles has been developed. The proposed formalism consistently outlines the principles of antisymmetrization and translational invariance. Compared with the traditional approach, the method is based on an expansion of the wave function on HO functions with different sizes in the Jacobi coordinates. The advantage of this treatment steams from the introduction of more appropriate degrees of freedom that better reflects the basic physics of the system. The efficiency of the method is based on the very fast computation procedure for Talmi-Moshinsky brackets calculations [16] . The computation of many-particle operators matrix elements in HO basis can be significantly simplified using the Talmi transformations. One of the novelties developed in this paper is the calculation of the Hamiltonian matrix elements on the HO functions with two different oscillator lengths by means of Talmi-Moshinsky brackets. This formalism is particularly well suited for very asymmetric systems (for example one light and two heavy particles). The complications of proposed approach as compared to the traditional one are due to the necessity to perform a double minimization on both different sizes in the Jacobi coordinates instead of a single minimization on an unique size parameter. Nevertheless, since this treatment grasps better the physical contents of the system, it may be expected that for a given number of HO quanta, the precision achieved can be increased as compared to the traditional approach.

The method was applied for estimation of ground state energies of a number of Coulomb three-body systems with two identical particles for zero HO excitation energy. The binding of ground state is obtained for all Coulomb three-body systems with two identical particles. It is consistent with well established results [17] . This is not the case in the traditional approach with only one oscillator length where in zeroth order approach the negative energy of ground state for very asymmetric systems cannot be obtained. For considered three-body systems, this result is confirmed by the analysis of the derived compact solution for ground state energy with only one size parameter. The advantages of the developed approach with different sizes in the Jacobi coordinates let us expect that the proposed simple and efficient zeroth order calculation procedure may be successfully generalized to any many-particle quantum system for testing of the existence of bound ground states.

In this paper we focused on the three-body systems where the interaction potential was limited to the Coulomb interaction only. The method is quite general, however, and can be applied to problems if other interaction potentials are used. The proposed approach may be generalized to problems of more than three particles. The addition of another particle introduces one more Jacobi coordinate with corresponding size parameter (for example three size parameters in case of four-body systems). The generalization of this approach may provide consistent and effective treatment of principle of translational invariance in many-particle quantum systems. This could greatly improve the zeroth order calculation results and considerable increase the rate of convergence of HO basis expansion.

Acknowledgements

The author would like to thank Prof. Gintautas P. Kamuntavičius for stimulating this work and his careful reading of this paper.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Friedrich, H.S. (2005) Theoretical Atomic Physics. 3rd Edition, Spinger, Berlin.
[2]	Faddeev, L.D. (1961) Soviet Physics JETP, 12, 1014-1019.
[3]	Yakubovsky, O.A. (1967) Soviet Journal of Nuclear Physics, 5, 937-951.
[4]	Kamuntavicius, G.P. (1986) Few-Body Systems, 1, 91-109. http://dx.doi.org/10.1007/BF01277077
[5]	Kamuntavicius, G.P. (1989) Soviet Journal Particles and Nuclei, 20, 109-140.
[6]	Deveikis, A. and Kamuntavicius, G.P. (1995) Lithuanian Journal of Physics, 35, 14-19.
[7]	Deveikis, A. and Kamuntavicius, G.P. (1996) Lithuanian Journal of Physics, 36, 83-95.
[8]	Navrátil, P. and Barrett, B.R. (1996) Physical Review C, 54, 2986-2995. http://dx.doi.org/10.1103/PhysRevC.54.2986
[9]	Deveikis, A. and Kamuntavicius, G.P. (1997) Lithuanian Journal of Physics, 37, 371-383.
[10]	Navrátil, P. and Barrett, B.R. (1998) Physical Review C, 57, 3119-3128. http://dx.doi.org/10.1103/PhysRevC.57.3119
[11]	Navrátil, P., Kamuntavicius, G.P. and Barrett, B.R. (2000) Physical Review C, 61, Article ID: 044001. http://dx.doi.org/10.1103/PhysRevC.61.044001
[12]	Kamuntavicius, G.P. (2014) Journal of Mathematical Physics, 55, Article ID: 042103. http://dx.doi.org/10.1063/1.4870617
[13]	Ancarani, L.U., Rodriguez, K.V. and Gasaneo, G. (2010) EPJ Web of Conferences, 3, Article ID: 02009.
[14]	Abramowitz, M. and Stegun, I.A. (1972) Handbook of Mathematical Functions. 9th Edition, National Bureau of Standards, Washington DC.
[15]	Varshalovich, D.A., Moskalev, A.N. and Khersonskii, V.K. (1988) Quantum Theory of Angular Momentum. World Scientific, Singapore. http://dx.doi.org/10.1142/0270
[16]	Kamuntavicius, G.P., Kalinauskas, R.K., Barrett, B.R., Mickevicius, S. and Germanas, D. (2001) Nuclear Physics A, 695, 191-201. http://dx.doi.org/10.1016/S0375-9474(01)01101-0
[17]	Hill, R.N. (1977) Journal of Mathematical Physics, 18, 2316-2330. http://dx.doi.org/10.1063/1.523241
[18]	Press, W.H., Teukolsky, S.A., Vetterling, W.T. and Flannery, B.P. (2007) Numerical Recipes: The Art of Scientific Computing. 3rd Edition, Cambridge University Press, New York.
[19]	Mohr, P.J., Taylor, B.N. and Newell, D.B. (2010) CODATA Recommended Values of the Fundamental Physical Constants. http://arxiv.org/abs/1203.5425
[20]	Liverts, E.Z. and Barnea, N. (2013) Computer Physics Communications, 184, 2596-2603. http://dx.doi.org/10.1016/j.cpc.2013.06.013