Category Theoretic Properties of the A. Rényi and C. Tsallis Entropies ()
Received 9 December 2015; accepted 26 January 2016; published 29 January 2016

1. Introduction
Because the measure of information is a basic scientific concept, in this work we develop a formalism in the framework of the category theory [14] [15] for the study of generalized entropies. The category theory is the branch of mathematics that plays a central role in the logical foundation and synthesis of the whole contemporary mathematics. In particular, the category theory allows avoiding the paradoxes of the classical set theory. Category theory has application in informatics [16] . In order to highlight the natural structures related to generalized entropies, we use the central concepts of the modern mathematics.
The paper is organized as follows. In the Section 2, Subsection 2.1, we define a special category related to measurable spaces (referred to as MES), enabling the introduction an associated basic functional zp (see the forthcoming Section for his exact definition). Both the Tsallis and Rényi entropies, as well as the distance in lp spaces, may be expressed in terms of this functional. In the Subsection 2.2, we define the direct product of the objects in MES and we prove that the functional zp satisfies a compatibility relation with respect to this product i.e., it is multiplicative. This multiplicative property is equivalent to the additivity of the Rényi entropy. In the Subsection 2.3, we define the disjoint sum (or the coproduct) of the objects in MES, and we prove that the functional zp satisfies a compatibility relation with respect to coproduct i.e., it is additive. Note that this property is equivalent to one of the postulates characterizing the Rényi entropy. The proofs that both product and coproduct possess a universal property and that the direct product and coproduct can also be defined for morphisms of the category MES, can be found in the Subsection 2.4. In the Subsection 2.5 we show that, by extending the category MES with the introduction of the unit object and the null object, the category MES becomes to a monoidal category.
Section 3 deals with the axiomatic characterization of the functional zp. We demonstrate that there exists a universal exponent p (the same for all the objects of the category) that characterizes completely the functional zp (hence, also the Tsallis or Rényi entropies) up to an arbitrary multiplicative factor. In Section 4, it is proven that the main properties of the Rényi entropy, which are used in the axiomatic and category theoretic formulation, can be reformulated in order to be generalized to the case of the generalized Rényi entropy (GRE). The symmetry properties of GRE are studied in Subsection 4.1. Appendix 1 shows that the Rényi divergence can be expressed in terms of the Rényi entropy. The proof of the universality (with respect to all the objects of the category MES) of the exponent defining the Rényi or Tsallis entropies can be found in Appendix 2. In Appendix 3 some algebraic results related to the symmetry of GRE are proved.
2. The Category-theoretic properties Related to Rényi and Tsallis Entropies
2.1. Definitions
Our definitions include as a particular case the original definition of the generalized entropies [5] [6] and [2] . Our basic construction that will play the role of the object of the category MES is derived from the well known concept of measurable space [17] [18] . Guided by statistical ideas, in order to take into account the negligible sets we specify also an sub-ideal of the σ-algebra of measurable sets. The objects of the category MES consist of triplets 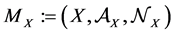 with X denoting the phase space (for instance, it is a symplectic manifold in the case of statistical physics or, in the case of elementary probability models, finite or denumerable set) and
with X denoting the phase space (for instance, it is a symplectic manifold in the case of statistical physics or, in the case of elementary probability models, finite or denumerable set) and 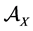 is the σ-algebra generated by a family of subsets of X, respectively. We also denote with
is the σ-algebra generated by a family of subsets of X, respectively. We also denote with 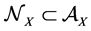 an ideal of the σ-algebra
an ideal of the σ-algebra 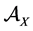 having the meaning of negligible sets. Let us now postulate the completeness property. From
having the meaning of negligible sets. Let us now postulate the completeness property. From 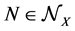 and
and 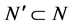 results
results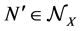 . The morphisms of the category MES with the source
. The morphisms of the category MES with the source 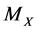 and range
and range 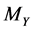 are the measurable maps Φ from x to y, which are nonsingular, i.e. such that
are the measurable maps Φ from x to y, which are nonsingular, i.e. such that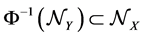 . From the completeness property results the ideal property, i.e. if
. From the completeness property results the ideal property, i.e. if 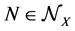 and
and 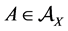 then
then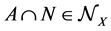 . Note that it is possible that
. Note that it is possible that 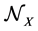 contains only the empty set (as, for example, in the case of atomic spaces).
contains only the empty set (as, for example, in the case of atomic spaces).
Remark 1 At first sight it would be more natural to consider the objects as measure space triplet 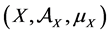 containing the measure
containing the measure![]() , and the morphisms as the measure preserving transformations. However, in this case we cannot define direct product or coproduct having universal property.
, and the morphisms as the measure preserving transformations. However, in this case we cannot define direct product or coproduct having universal property.
We denote with![]() , or with
, or with![]() , the cone with all σ-finite positive measures over
, the cone with all σ-finite positive measures over ![]() that are compatible with
that are compatible with ![]() (i.e.,
(i.e., ![]() iff for all
iff for all ![]() we have
we have![]() ). For a given
). For a given ![]() and
and![]() , we denote with
, we denote with ![]() the Banach space (
the Banach space (![]() ) or the Fréchet space (
) or the Fréchet space (![]() ) of functions
) of functions ![]() that are measurable modulo
that are measurable modulo ![]() and have
and have
finite norm (pseudo norm, respectively): more precisely,![]() . In the sequel, we shall denote
. In the sequel, we shall denote
![]() (1)
(1)
for some non-negative density![]() . The generalized entropies are defined for probability density functions (PDF) satisfying the conditions
. The generalized entropies are defined for probability density functions (PDF) satisfying the conditions
![]() (2)
(2)
![]() (3)
(3)
where ![]() and
and![]() . The probability
. The probability ![]() can be represented by PDF as follows
can be represented by PDF as follows
![]() (4)
(4)
![]() (5)
(5)
In this framework, for a given measurable space ![]() and measure
and measure![]() , the classical Boltzmann-Gibbs-Shannon entropy functional is given by
, the classical Boltzmann-Gibbs-Shannon entropy functional is given by
![]() (6)
(6)
which in the case of discrete distribution, X a denumerable set, ![]() the counting measure, give the popular form
the counting measure, give the popular form
![]() (7)
(7)
For a given measurable space![]() , the generalizations of the A. Rényi [2] and C. Tsallis [5] [6] entropies, involves the functional
, the generalizations of the A. Rényi [2] and C. Tsallis [5] [6] entropies, involves the functional ![]() given by Equation (1). The functional
given by Equation (1). The functional ![]() is related to the norm of
is related to the norm of
the density ρ in the Banach space for ![]() [18] , and to the pseudo-norm
[18] , and to the pseudo-norm ![]() for
for ![]() [17] [19] , through the obvious relations
[17] [19] , through the obvious relations
![]() (8)
(8)
![]() (9)
(9)
These relations give the geometrical interpretation of the generalized entropies (for further information Refs to [13] ).
Remark 2 The study of the generalized entropies helps us to better understand the classical entropy. For![]() , the functional
, the functional ![]() is the classical Lp norm, and for
is the classical Lp norm, and for ![]() the functional
the functional ![]() is the exotic Lp-norm [19] . For
is the exotic Lp-norm [19] . For ![]() the Lp spaces are reflexive, the Maxent problem is equivalent to the minimal Lp distance problem with restrictions [13] , or to the minimal
the Lp spaces are reflexive, the Maxent problem is equivalent to the minimal Lp distance problem with restrictions [13] , or to the minimal![]() . For
. For![]() , the Lp spaces has, in general, trivial duals, the Maxent problem is equivalent to the maximal Lp distance or the maximal
, the Lp spaces has, in general, trivial duals, the Maxent problem is equivalent to the maximal Lp distance or the maximal ![]() (see [13] ). The case
(see [13] ). The case![]() , which corresponds to the classical Shannon entropy, is just the border point between two radically different functional-analytic properties.
, which corresponds to the classical Shannon entropy, is just the border point between two radically different functional-analytic properties.
The corresponding generalized entropy![]() , proposed by A. Rényi [2] , and the entropy,
, proposed by A. Rényi [2] , and the entropy, ![]() , proposed by C. Tsallis [5] , [6] are given by
, proposed by C. Tsallis [5] , [6] are given by
![]() (10)
(10)
![]() (11)
(11)
Consider now a measure space ![]() with σ-finite measure n, and let us denote with
with σ-finite measure n, and let us denote with![]() ,
, ![]() two probability densities:
two probability densities:
![]()
Note that the Rényi divergence [2] [12]
![]() (12)
(12)
is related to the Rényi entropies (see Appendix 1). Note that when x is a finite or denumerable set, if we denote with ![]() the probabilities of element
the probabilities of element![]() , the measure
, the measure ![]() is the counting measure on the space x (equal to the number of elements in a subset), and the family of null sets
is the counting measure on the space x (equal to the number of elements in a subset), and the family of null sets ![]() then, from the previous Equstions (1), (10), (11) we get the original definitions from Ref. [2] [5] [6]
then, from the previous Equstions (1), (10), (11) we get the original definitions from Ref. [2] [5] [6]
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
Remark that, in this particular case, ![]() , as well as
, as well as![]() , are Lesche stable [20] . Note that, from Equations (6), (10) and (11), results
, are Lesche stable [20] . Note that, from Equations (6), (10) and (11), results
![]() (16)
(16)
2.2. Direct Product of Measurable spaces and the multiplicative Property of Zp[MX, μX, ρX]
In the framework of the our formalism, the multiplicative property is the counterpart of the Postulate 4 in the Rényi theory [2] . In the following we overload the tensor product notation “![]() ”; its meaning results from the nature of the operand. Denote the direct product of two measurable spaces
”; its meaning results from the nature of the operand. Denote the direct product of two measurable spaces ![]() and
and ![]() by
by![]() , defined as follows
, defined as follows
![]() (17)
(17)
Here ![]() is the Cartesian product of the phase spaces X and Y, while the σ-algebra
is the Cartesian product of the phase spaces X and Y, while the σ-algebra ![]() is the smallest σ-algebra such that it contains all of the elements of the Cartesian product
is the smallest σ-algebra such that it contains all of the elements of the Cartesian product![]() . The null set ideal
. The null set ideal ![]() is generated by the family
is generated by the family![]() . Note that if
. Note that if ![]() and
and ![]() then their direct product satisfies the condition
then their direct product satisfies the condition ![]() (we denote it also by the same symbol). The measure
(we denote it also by the same symbol). The measure ![]() acting on
acting on ![]() is defined by extension by denu- merable additivity, starting from the product subsets:
is defined by extension by denu- merable additivity, starting from the product subsets:
![]() (18)
(18)
![]() (19)
(19)
Consider now the measures![]() ,
, ![]() , and the densities
, and the densities ![]() and
and![]() . The following function is also denoted with the same symbol
. The following function is also denoted with the same symbol
![]() (20)
(20)
with
![]() (21)
(21)
![]() (22)
(22)
We have the following basic proposition
Proposition 3 Let![]() ,
, ![]() are normalized PDF
are normalized PDF
![]() (23)
(23)
Then we have
![]() (24)
(24)
![]() (25)
(25)
The validity of this statement follows directly from the definitions of the direct product, the Rényi entropy and the functional zp.
2.3. Coproduct of measurable spaces and theadditivity of the Functional Zp[MX, μX, ρX]
Let us study now the property encoded in the Postulate 5’ related to the Rényi entropy theory (Ref. [2] ), trans- cribed in the measure theoretic and category language and re -expressed in the term of the functional ![]() . Also in this case, we overload the notation
. Also in this case, we overload the notation![]() , for the disjoint sum from the set theory. Its precise meaning will be clear from the nature of the operands. In the following we investigate the functorial properties, related to Postulate 5’, of the functional
, for the disjoint sum from the set theory. Its precise meaning will be clear from the nature of the operands. In the following we investigate the functorial properties, related to Postulate 5’, of the functional![]() , in analogy to Proposition 3. To this end we introduce the following
, in analogy to Proposition 3. To this end we introduce the following
Definition 4 The coproduct of measurable spaces ![]() and
and ![]() will be denoted by
will be denoted by ![]() and have the following structure
and have the following structure
![]() (26)
(26)
Here, ![]() is the disjoint sum of the sets x and y, and
is the disjoint sum of the sets x and y, and ![]() is the smallest σ-algebra that contains all of the sets of the form
is the smallest σ-algebra that contains all of the sets of the form![]() , with
, with ![]() and
and![]() , respectively. Moreover, the new null set ideal
, respectively. Moreover, the new null set ideal ![]() is the smallest σ-algebra generated by the family
is the smallest σ-algebra generated by the family ![]() with
with ![]() and
and![]() . Let the measures
. Let the measures![]() ,
, ![]() and the weights
and the weights![]() ,
, ![]() and
and![]() . The measure
. The measure ![]() acts on the σ-algebra
acts on the σ-algebra ![]() and it is defined uniquely as the continuation by denumer- able additivity from the property
and it is defined uniquely as the continuation by denumer- able additivity from the property
![]() (27)
(27)
![]() (28)
(28)
Let ![]() and
and ![]() . We define the function
. We define the function ![]() as follows
as follows
![]()
![]()
We restrict our definition of coproduct to finite terms. An example of (denumerable infinite) coproduct is the grand canonical ensemble.
Remark 5 If ![]() and
and ![]() are probability measures, then the measure
are probability measures, then the measure ![]() is a probability measure if
is a probability measure if ![]() .
.
From the previous definition of the direct sum and the functional ![]() the following obvious proposition results
the following obvious proposition results
Proposition 6 The reformulation of the Postulate 5’ (Ref. [2] ) reads: the functional ![]() is additive with respect to the direct sum of measurable spaces
is additive with respect to the direct sum of measurable spaces
![]() (29)
(29)
2.4. Universal Properties of the direct product and Direct Sum in the category of Measurable spaces
In the following we prove that the basic binary operations on measurable spaces, the direct product and the direct sum, defined in the previous section, have universality properties in the category of measurable spaces MES.
Consider the direct product ![]() of measurable spaces
of measurable spaces ![]() and
and ![]() . Observe that the canonical projections
. Observe that the canonical projections![]() ,
, ![]() , are measurable and induce the morphisms
, are measurable and induce the morphisms ![]() and
and ![]() between the objects of MES. We have the following
between the objects of MES. We have the following
Proposition 7 In the category MES the applications![]() ,
, ![]() , which are naturally induced by canonical projections
, which are naturally induced by canonical projections ![]() and
and![]() , are morphisms.
, are morphisms.
Proof. The measurability of ![]() is direct consequence of the fact that the canonical projection maps are measurable, in fact the measurability of the canonical projections is an alternative definition of the product of σ algebras. The nonsingularity property
is direct consequence of the fact that the canonical projection maps are measurable, in fact the measurability of the canonical projections is an alternative definition of the product of σ algebras. The nonsingularity property ![]() results from
results from![]() . ■
. ■
From the previous Proposition 7 results immediately the following Theorem
Theorem 8 In the category MES, the direct product has the universal property. Let![]() .
. ![]() and
and ![]() measurable spaces that are objects of the category MES, such that there exists morphisms
measurable spaces that are objects of the category MES, such that there exists morphisms ![]() and
and![]() . Then there exists an unique morphism
. Then there exists an unique morphism ![]() such that
such that
![]() (30)
(30)
![]() (31)
(31)
where![]() ,
, ![]() are the morphism defined in Proposition 7.
are the morphism defined in Proposition 7.
Proof. The morphism θ is induced by the application ![]() defined as
defined as ![]() . and it is unique. In order to prove that θ is a morphism we have to prove that t is measurable and it is nonsingular. To prove that
. and it is unique. In order to prove that θ is a morphism we have to prove that t is measurable and it is nonsingular. To prove that ![]() is measurable, we recall that it is sufficient to prove that, for all
is measurable, we recall that it is sufficient to prove that, for all![]() ,
, ![]() , we have the property
, we have the property![]() , a property resulting from the measurability of
, a property resulting from the measurability of ![]() and
and![]() . Note that to prove the inclusion
. Note that to prove the inclusion![]() , it is sufficient to demonstrate for the generating subsets
, it is sufficient to demonstrate for the generating subsets ![]() (which follows from the nonsingularity of
(which follows from the nonsingularity of ![]() and
and![]() ) that this is the consequence of the nonsingularity of
) that this is the consequence of the nonsingularity of![]() . ■
. ■
In conclusion the direct product operation has the natural functorial property, so the multiplicative property Equation (24) of the functional ![]() appears as an algebraic compatibility property. By simple reversal of the arrows, we are lead to the corresponding universality property of the coproduct in the category MES. We have the following obvious proposition
appears as an algebraic compatibility property. By simple reversal of the arrows, we are lead to the corresponding universality property of the coproduct in the category MES. We have the following obvious proposition
Proposition 9 In the category MES, consider the objects![]() ,
,![]() . The applications
. The applications ![]() and
and![]() , induced naturally by the canonical injections
, induced naturally by the canonical injections![]() ,
, ![]() , are morphism in the category MES.
, are morphism in the category MES.
Proof. The injections![]() ,
, ![]() are measurable. Suppose that
are measurable. Suppose that![]() , with
, with![]() ,
, ![]() (see Definition 4). Then,
(see Definition 4). Then, ![]() ,
, ![]() , so
, so ![]() and
and ![]() are nonsingular, which completes the proof that
are nonsingular, which completes the proof that![]() ,
, ![]() are morphisms in the category mes. ■
are morphisms in the category mes. ■
By reversing the arrows, in analogy to the Theorem 8, we obtain the following result.
Theorem 10 In the category mes the direct sum of the objects has the following universality property. Let denote with![]() ,
, ![]() and
and ![]() measurable spaces that are objects of the category mes, such that there exists morphisms
measurable spaces that are objects of the category mes, such that there exists morphisms ![]() and
and![]() . Then, there exists an unique morphism
. Then, there exists an unique morphism ![]() such that
such that
![]()
![]()
where![]() ,
, ![]() are the morphisms defined in Proposition 9.
are the morphisms defined in Proposition 9.
Proof. The morphism ![]() is induced by the map
is induced by the map ![]() defined as follows. If
defined as follows. If ![]() then
then![]() , and in the case
, and in the case![]() , then
, then![]() . The measurability of the map g results from the measurability of
. The measurability of the map g results from the measurability of ![]() and
and![]() . The inclusion
. The inclusion ![]() results from the nonsingularity of
results from the nonsingularity of ![]() and
and![]() .
.
In conclusion, the direct sum operation has natural category theoretic properties. Hence, the additivity property Equation (29) of the functional ![]() is not an artificial construction.
is not an artificial construction.
2.5. The Monoidal Categories associated to product and Coproduct
We recall the following
Proposition 11 [15] Let ![]() be a category such that for all objects
be a category such that for all objects ![]() exists their direct product
exists their direct product![]() , having the universal property. Then, there exists a covariant functor F from the product category to
, having the universal property. Then, there exists a covariant functor F from the product category to![]() ,
, ![]() , defined as follows. For the object
, defined as follows. For the object ![]() of
of![]() , where
, where ![]() are objects of
are objects of![]() , we have
, we have
![]()
For the pair of morphisms ![]() with
with![]() ,
, ![]() , from the category
, from the category ![]() there exists an unique morphism w in the category
there exists an unique morphism w in the category![]() ,
, ![]() uniquely fixed by the conditions
uniquely fixed by the conditions
![]()
![]()
![]()
We denoted with![]() ,
, ![]() the projections from
the projections from![]() ,
, ![]() , and
, and ![]() are
are ![]() the projections from
the projections from![]() ,
,![]() . The map
. The map ![]() has the functorial property.
has the functorial property.
Let ![]() and
and![]() . Then,
. Then,
![]()
If in the category ![]() we have an unit object, then
we have an unit object, then ![]() is a monoidal category.
is a monoidal category.
Similarly, by duality arguments, we have the following result for the direct sum (coproduct)
Proposition 12 [15] Let ![]() be a category such that for all objects a, B from
be a category such that for all objects a, B from ![]() exists their direct sum
exists their direct sum![]() , having the universal property. Then, there exists a covariant functor G from the product category
, having the universal property. Then, there exists a covariant functor G from the product category ![]() defined as follows. For the object (A,b) of
defined as follows. For the object (A,b) of![]() , where a, B are objects of
, where a, B are objects of ![]() we have
we have
![]()
For the pair of morphisms![]() , with
, with ![]() and
and![]() , from the category
, from the category ![]() there exists an unique morphism w in the category
there exists an unique morphism w in the category![]() ,
, ![]() uniquely fixed by the conditions
uniquely fixed by the conditions
![]()
![]()
![]()
We denoted with![]() ,
, ![]() the canonical injections from
the canonical injections from![]() ,
, ![]() , and with
, and with![]() ,
, ![]() the injections from
the injections from![]() ,
,![]() . The association
. The association ![]() has the func- torial property. Let
has the func- torial property. Let ![]() and
and ![]() then,
then,
![]()
If in the category ![]() we have a null object then,
we have a null object then, ![]() is a monoidal category with respect to direct sum.
is a monoidal category with respect to direct sum.
We emphasize that, despite the fact that the construction of the direct sum is dual to the direct product, from the previous proposition (12) the functor G is a covariant functor. In the category mes we have an unit object as well as the null object. The unit object is denoted with![]() , where 1 is the one point set [15] ,
, where 1 is the one point set [15] , ![]() is the trivial σ-algebra consisting in the one point set 1,
is the trivial σ-algebra consisting in the one point set 1, ![]() , and
, and![]() , respectively. The (more or less for- mal) null object
, respectively. The (more or less for- mal) null object![]() , with respect to the direct sum, is the object generated by the empty set
, with respect to the direct sum, is the object generated by the empty set![]() . So we have the following
. So we have the following
Conclusion 13 The category MES is a monoidal category both with respect to the product ![]() and the coproduct
and the coproduct![]() .
.
3. Axioms
We expose another approach, based on category theory, to the problem of the naturalness of the choice of the family of functions ![]() used in the definition of the entropy [2] . We prove that this problem may be treated if we take into account the additivity and the multiplicative properties of the functional
used in the definition of the entropy [2] . We prove that this problem may be treated if we take into account the additivity and the multiplicative properties of the functional![]() . We mention that a possible candidate for the generalization of the symmetry Postulate 1 [2] is the requirement of invariance of the generalized entropy under measure preserving transformations. Recall that the group generated by finite permu- tations is the maximal measure preserving group with respect to the counting measure. The problem is that there are plenty of measures such that the measure preserving group is trivial (for instance, the atomic measure for 2 element set with
. We mention that a possible candidate for the generalization of the symmetry Postulate 1 [2] is the requirement of invariance of the generalized entropy under measure preserving transformations. Recall that the group generated by finite permu- tations is the maximal measure preserving group with respect to the counting measure. The problem is that there are plenty of measures such that the measure preserving group is trivial (for instance, the atomic measure for 2 element set with![]() ). To avoid this problem, we observe that Postulate 1 and Postulate 5’ in the original Rényi theory [2] can be generalized as follows. For a given measurable function
). To avoid this problem, we observe that Postulate 1 and Postulate 5’ in the original Rényi theory [2] can be generalized as follows. For a given measurable function ![]() on the mea- sured space
on the mea- sured space ![]() and
and![]() , let us define
, let us define
![]() (32)
(32)
Note that ![]() is invariant under measure preserving transformations. In addition
is invariant under measure preserving transformations. In addition
![]() (33)
(33)
Then, the Postulate 1 (the symmetry property) and Postulate 5’ (the additivity property expressed in Propo- sition 6) can be generalized as follows. Postulate 1 & Postulate 5’
![]() (34)
(34)
![]() (35)
(35)
for some Borel measurable function ![]() with
with
![]() (36)
(36)
The last requirement result by considering the case when the support of ![]() is concentrated on a proper subset of x and by using Equation (29). The generalization of the Postulate 2 (the continuity property) is straightforward. Be
is concentrated on a proper subset of x and by using Equation (29). The generalization of the Postulate 2 (the continuity property) is straightforward. Be ![]() continuos and
continuos and![]() , we get
, we get
![]() (37)
(37)
In our settings, the analog of the Postulate 4 (the additivity property) [2] is the multiplicative property given by Equation (24) and Proposition 3. By using Equations (24), (34), (36) and (37), and by continuity of the functions![]() ,
, ![]() ,
, ![]() for all
for all![]() , we obtain the following functional equation (valid almost every- where)
, we obtain the following functional equation (valid almost every- where)
![]() (38)
(38)
By arguments similar to the proof of the uniqueness, from Theorem 2 [2] ), we get Equation (33) (for details see Appendix 2): there exists an universal family of functions, independent of X, parametrized by the positive parameter p such that
![]() (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
4. The Generalized Rényi Entropy (GRE)
Remark that all of the definitions of the classical, Rényi, Tsallis entropies contains only set theoretic and mea- sure theoretic concepts, no supposition on the auxiliary algebraic or differentiable structure associated to the measure space are assumed, so their definitions can be used t, continuos or discrete distributions. In the case of discrete measured space the classical definitions of the entropies Equations (7), (13)-(15) are invariant under the permutation group of the elements of the discrete set. This invariance encodes the assumption of complete apriory lack of information about the physical system, this absolute ignorance is lifted by the specification of the probability density function. On the other hand, consider the case when the measure space has the product structure
![]() (42)
(42)
such that
![]() (43)
(43)
![]() (44)
(44)
![]() (45)
(45)
Suppose that the probability measure on ![]() is given by
is given by
![]() (46)
(46)
The GRE’s associated are [13]
![]() (47)
(47)
![]() (48)
(48)
![]() (49)
(49)
We remark that in the definitions Equation (48), the role of the variables ![]() can be inverted. The range
can be inverted. The range ![]() of entropy parameters is given by
of entropy parameters is given by
![]()
![]()
In the limit case![]() , we obtain the Shannon entropy. We remark that in the definitions Equation (48), the role of the variables
, we obtain the Shannon entropy. We remark that in the definitions Equation (48), the role of the variables ![]() can be inverted. In the following we study the compatibility of the GRE with the axioms that define the classical Rényi entropy.
can be inverted. In the following we study the compatibility of the GRE with the axioms that define the classical Rényi entropy.
4.1. Symmetry Properties of GRE
In order to prove that in the case of the GRE the symmetry group is reduced to some subgroup, we consider only a special case: the spaces ![]() are finite sets, denoted as
are finite sets, denoted as![]() ,
, ![]() , the measures
, the measures![]() ,
, ![]() are the counting measures and denote
are the counting measures and denote ![]() the corresponding probabilities. We have
the corresponding probabilities. We have
![]() (50)
(50)
We use the array notation ![]() In this case, the Rényi entropy is
In this case, the Rényi entropy is
![]() (51)
(51)
It is invariant under the transformation (see Lemma 16)
![]() (52)
(52)
![]() (53)
(53)
where the transformation ![]() is an arbitrary permutation of the finite index set with Na elements:
is an arbitrary permutation of the finite index set with Na elements:![]() . In this case, the permutation group
. In this case, the permutation group ![]() plays the role of the measure preserving transformations. The corresponding GRE’s according to Equations (47)-(49) are the following
plays the role of the measure preserving transformations. The corresponding GRE’s according to Equations (47)-(49) are the following
![]() (54)
(54)
![]() (55)
(55)
![]() (56)
(56)
Suppose we are in general case, when the indices i, a has completely different physical interpretation. Its is clear that the measure of information of such a system cannot be invariant under the permutation group ![]() with
with ![]() elements. It is expected to be invariant only on the separate
elements. It is expected to be invariant only on the separate ![]() permutation from the group
permutation from the group ![]() related to index i and
related to index i and ![]() permutation of
permutation of![]() , related to the index a, more exactly the invariance group is expected to contain a proper subgroup of
, related to the index a, more exactly the invariance group is expected to contain a proper subgroup of![]() , generated by
, generated by ![]() and
and![]() . So we are interested to find some subgroups
. So we are interested to find some subgroups ![]() of transformations
of transformations ![]() such that for all
such that for all ![]() we have
we have
![]() (57)
(57)
![]() (58)
(58)
Similarly we are interested to find the subgroup ![]() which consists of the transformations
which consists of the transformations ![]() such that
such that
![]() (59)
(59)
![]() (60)
(60)
By using the Corollary 17, we obtain the following conclusion concerning the symmetry group of GRE, com- pared to the symmetry group of the classical Rényi or Tsallis entropies.
Proposition 14 The symmetry group ![]() of the GRE
of the GRE ![]() is reduced from the full permutation group
is reduced from the full permutation group ![]() to the subset of transformations of the form
to the subset of transformations of the form
![]() (61)
(61)
where ![]() is a permutation of the
is a permutation of the ![]() and for each fixed
and for each fixed ![]() each of the map
each of the map ![]() is the permutation of the set
is the permutation of the set![]() . Similarly for the map
. Similarly for the map![]() , we have
, we have ![]() (Equation (60)) if and only if it is the form
(Equation (60)) if and only if it is the form
![]() (62)
(62)
where the map ![]() is a permutation of the set
is a permutation of the set ![]() and for each fixed
and for each fixed ![]() the map
the map ![]() is a permutation of the set
is a permutation of the set![]() . The subgroup
. The subgroup ![]() which consists of all
which consists of all ![]() that leave invariant both of the entropies
that leave invariant both of the entropies ![]() and
and ![]()
![]() (63)
(63)
![]() (64)
(64)
![]() (65)
(65)
is the direct product ![]() and
and ![]() iff
iff
![]() (66)
(66)
where ![]() is a permutation of
is a permutation of ![]() and
and ![]() is a permutation of
is a permutation of ![]()
In conclusion, in this particular case, the symmetry group associated to GRE’s ![]()
![]() is reduced to the direct product of the transformations that separately preserves the measure
is reduced to the direct product of the transformations that separately preserves the measure ![]() respectively
respectively![]() , in accord with the different physical interpretation of the variables x and y. The proof for the more subtle general case will be the subject of following studies.
, in accord with the different physical interpretation of the variables x and y. The proof for the more subtle general case will be the subject of following studies.
4.2. The Additivity of GRE, Multiplicative property of ![]()
According to Equations (42)-(49), the additivity of the GRE is equivalent to the multiplicative property of the functionals![]() . In analogy to the properties from Equations (24), (25) we have a perfect correspondence with the classical case [13] . Consider the case when the measured spaces, measures, densities entering in the definition of the GRE from Equations (42)-(46) are decomposed as follows
. In analogy to the properties from Equations (24), (25) we have a perfect correspondence with the classical case [13] . Consider the case when the measured spaces, measures, densities entering in the definition of the GRE from Equations (42)-(46) are decomposed as follows
![]()
![]()
![]()
![]()
Under these assumptions and with the notations Equations (47) and (49), we have the following functorial property with respect to the direct product:
![]()
![]()
4.3. Additivity of the functionals ![]() withrespect to the direct sum
withrespect to the direct sum
It is possible to extend, partially, the additivity property from Proposition 6. Consider the measured space defined in Equations (42)-(46) and suppose that the space X and the related objects has the following decom- position in direct sum, similar to the Definition 4
![]() (67)
(67)
We define the measure
![]() (68)
(68)
![]() similar to Equations (27), (28), with
similar to Equations (27), (28), with ![]() and from the densities
and from the densities ![]() de- fined in the
de- fined in the ![]() and
and ![]() defined in the
defined in the![]() , we define the density
, we define the density
![]() (69)
(69)
similar to Definition 4
![]() (70)
(70)
![]() (71)
(71)
Under previous conditions Equations (67)-(71), we have the following additivity result:
![]() (72)
(72)
We obtain a similar result for the functional ![]() if we consider a decomposition
if we consider a decomposition![]() . The Equation (72) is the equivalent of the Postulate 5’ from the case of the classical Rényi entropy. At this stage we remark another anisotropy effect: the different mathematical properties related to the “outer integral over X” and the “inner integral over Y” in the definition Equation (48).
. The Equation (72) is the equivalent of the Postulate 5’ from the case of the classical Rényi entropy. At this stage we remark another anisotropy effect: the different mathematical properties related to the “outer integral over X” and the “inner integral over Y” in the definition Equation (48).
5. Summary and Conclusions
We proved that the most natural setting for treating the axiomatic approach to the study of definitions of measures of information or uncertainty, is the formalism of measure spaces and of the category theory. The Rényi divergence can be reduced to the Rényi entropy in our measure theoretic formalism. Category theory was invented for the most difficult, apparently contradictory aspects of the foundation of mathematics. In this respect, we introduced a category of measurable spaces MES. We proved that in the category MES existed the direct product and the direct sum, having universal properties. We proved that the functional ![]() de- fined in Equation (1), which appeared in the definition of both Rényi and Tsallis entropies, had algebraic com- patibility properties with respect to direct product and direct sum, as shown in Equations (24) and (29).
de- fined in Equation (1), which appeared in the definition of both Rényi and Tsallis entropies, had algebraic com- patibility properties with respect to direct product and direct sum, as shown in Equations (24) and (29).
The main conclusions may be summarized as follows:
1) The natural measure of the quantity of information is the family of functionals ![]() given by Equation (1), (defined in the Fréchet space for
given by Equation (1), (defined in the Fréchet space for![]() , and in the Banach space for
, and in the Banach space for![]() ), and the classical Shannon entropy by Equation (6);
), and the classical Shannon entropy by Equation (6);
2)The category MES is the natural framework for treating the problems related to the measure of the infor- mation, in particular in reformulating the Rényi axioms;
3) The category MES is a monoidal category with respect to direct product and coproduct and the functional ![]() has natural compatibility properties with respect to the product (it is multiplicative) and the coproduct (it is additive);
has natural compatibility properties with respect to the product (it is multiplicative) and the coproduct (it is additive);
4) Up to a multiplicative constant, it is possible to recover the exact form of the functional ![]() defining the generalized entropies from a system of axioms that generalize the ones adopted by Rényi [2] .
defining the generalized entropies from a system of axioms that generalize the ones adopted by Rényi [2] .
5) The GRE ![]() has similar additivity property with respect to the direct product de- composition of the spaces X, Y.
has similar additivity property with respect to the direct product de- composition of the spaces X, Y.
6) The symmetry group of ![]() is reduced to a combination of the symmetry group related to the measured spaces
is reduced to a combination of the symmetry group related to the measured spaces ![]() and
and ![]() that is a proper subgroup of the full measure preserving group of
that is a proper subgroup of the full measure preserving group of ![]() that is the symmetry group of the classical Rényi entropy.
that is the symmetry group of the classical Rényi entropy.
7) The Postulate 5'’of the classical Rényi entropy appears in the case of GRE as the additivity property of the functional ![]() with respect to direct sum decomposition of the space X. This asymmetry with respect to space Y is a new manifestation of the anisotropy.
with respect to direct sum decomposition of the space X. This asymmetry with respect to space Y is a new manifestation of the anisotropy.
Acknowledgements
The authors are grateful to Prof. M. Van Schoor and Dr D. Van Eester from Royal Military School, Brussels. György Steinbrecher is grateful to Prof. C. P. Niculescu from Mathematics Department, University of Craiova, Romania, and S. Barasch for discussions on category theory. Giorgio Sonnino is also grateful to Prof. P. Nar- done and Dr. P. Peeters of the Université Libre de Bruxelles (ULB) for useful discussions and suggestions.
Appendix
A1. Rényi Divergence and entropy
Suppose to have a measurable space ![]() with a finite or σ-finite measure μ and a normalized PDF
with a finite or σ-finite measure μ and a normalized PDF![]() , i.e.
, i.e.![]() . Only in this subsection we adopt the following definitions
. Only in this subsection we adopt the following definitions
![]() (73)
(73)
![]() (74)
(74)
Consider now a measurable space ![]() with σ-finite measure n. We also denote with
with σ-finite measure n. We also denote with![]() ,
, ![]() two probability densities, satisfying the condition
two probability densities, satisfying the condition
![]() (75)
(75)
The Rényi divergence reads
![]() (76)
(76)
![]()
According to the Equations (73, 74, 76) and normalization Equation (75), we get
![]() (77)
(77)
A2. Solution of the functional Equation Equation (38)
Using Equation (35) with![]() , we note that we can use the double logarithmic scale by performing the following change of variables
, we note that we can use the double logarithmic scale by performing the following change of variables
![]() (78)
(78)
![]() (79)
(79)
![]() (80)
(80)
Hence, Equation (38) reads
![]() (81)
(81)
In the particular case ![]() from Equation (81), we obtain
from Equation (81), we obtain
![]() (82)
(82)
From Equations (81), (82) results
![]() (83)
(83)
We select in Equation (83) ![]()
![]() (84)
(84)
and the following equation results
![]() (85)
(85)
Remark t hat putting in Equation (84) ![]() we obtain an identity, so
we obtain an identity, so ![]() is a free parameter . Observe that Equation (85) admits the particular constant solution
is a free parameter . Observe that Equation (85) admits the particular constant solution
![]() (86)
(86)
The general solution of corresponding homogenous equation
![]() (87)
(87)
may be found by using again the continuity of the function ![]() (See also [21] I.3.1, page 8, we do not use here the differentiability of
(See also [21] I.3.1, page 8, we do not use here the differentiability of![]() ), i.e.,
), i.e.,
![]() (88)
(88)
Here ![]() is a constant, that, at this stage, still depends on the object XY of the category mes. In the con- tinuation we prove that the constant is “universal”, it is the same for all of the objects of the category mes.
is a constant, that, at this stage, still depends on the object XY of the category mes. In the con- tinuation we prove that the constant is “universal”, it is the same for all of the objects of the category mes.
The general solution of the Equation (85) reads
![]() (89)
(89)
and similarly we have for all of the object of the category mes
![]() (90)
(90)
![]() (91)
(91)
By using Equations (81), (89), (90), (91), we get the universal linear slope p
![]()
![]()
![]()
and, by Equations (78)-(80), up to undetermined multiplicative constants![]() ,
, ![]() , we find Equations (39)-(41).
, we find Equations (39)-(41).
A3. Some Algebraic Result
Lemma 16 Let ![]() positive numbers. If for all
positive numbers. If for all ![]() we have
we have
![]() (92)
(92)
where ![]() then there exists a permutation of the set
then there exists a permutation of the set![]() ,
, ![]() such that
such that
![]() (93)
(93)
Proof. We proceed by induction. For ![]() clear, suppose that the Lemma is valid for
clear, suppose that the Lemma is valid for ![]() and suppose, ad absurdum that
and suppose, ad absurdum that![]() . Taking the limit
. Taking the limit ![]() in Equation (92) we find a con- tradiction, so
in Equation (92) we find a con- tradiction, so ![]() which completes the induction step. ■
which completes the induction step. ■
By using the previous Lemma 16 in two successive steps, with ![]() respectively
respectively![]() , we find the following
, we find the following
Corollary 17 Suppose that for all ![]() we have
we have
![]() (94)
(94)
where![]() , with
, with ![]() and
and![]() , the permutation group of na elements is indexed by the pair
, the permutation group of na elements is indexed by the pair![]() . Then
. Then
![]() (95)
(95)
where the map ![]() is a permutation of the set
is a permutation of the set ![]() and for each fixed
and for each fixed ![]() each of the maps
each of the maps ![]() are permutations of the set
are permutations of the set![]() .
.