Stability and Boundedness of Solutions of Certain Non-Autonomous Third Order Nonlinear Differential Equations ()
Received 6 December 2015; accepted 23 January 2016; published 27 January 2016

1. Introduction
We shall be concerned here, with stability and boundedness of solutions of the third order, non-linear, non- autonomous differential equation of the form:
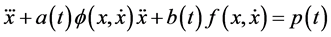 (1.1)
(1.1)
where a(t), b(t) are positive continuously differentiable functions and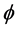 , f and p are continuous real-valued functions depending only on the arguments shown, and the dots indicate the differentiation with respect to t. Moreover, the existence and uniqueness of solutions of (1.1) will be assumed.
, f and p are continuous real-valued functions depending only on the arguments shown, and the dots indicate the differentiation with respect to t. Moreover, the existence and uniqueness of solutions of (1.1) will be assumed.
The Lyapunov function or functional approach has been a powerful tool to ascertain the stability and boundedness of solutions of certain differential equations. Up to now, perhaps, the most effective method to determine the stability and boundedness of solutions of non-linear differential equations is still the Lyapunov’s direct (or second) method. The major advantage of this method is that stability in the large and boundedness of solutions can be obtained without any prior knowledge of solutions. Today, this method is widely recognized as an excellent tool not only in the study of differential equations but also in the theory of control systems, dynamical systems, systems with time lag, power system analysis, time varying non-linear feedback systems, and so on. Its chief characteristic is the construction of a scalar function or functional, namely, the Lyapunov function or functional. This function or functional and its time derivative along the system under consideration must satisfy some fundamental inequalities. But, finding an appropriate Lyapunov function or functional is in general a difficult task. See [1] .
Stability analysis and boundedness of solutions of nonlinear systems are important area of current research and many concept of stability and boundedness of solutions have in the past been studied by several authors. See for instance, a survey book, Ressig et al. [2] and in a sequence of results by [3] - [8] . With respect to our observation in the relevant literature, these authors consider stability, asymptotic behavior and boundedness of
solutions of Equation (1.1) for which 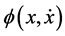 equals any of
equals any of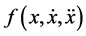 ,
, 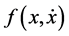 ,
,  and
and 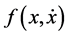 equals
equals , with
, with . The special case for which
. The special case for which ,
, 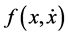 ,
,  and
and 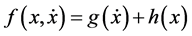 with
with 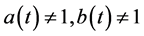 have received little attention due to the difficulty in constructing suitable scalar function. For example, see [9] - [12] . However, no work based on (1.1) was found. The result here will be different from those mentioned.
have received little attention due to the difficulty in constructing suitable scalar function. For example, see [9] - [12] . However, no work based on (1.1) was found. The result here will be different from those mentioned.
The motivation for the present work is derived from the papers of the authors mentioned above. Our aim is to extend their results to the very special case in Equation (1.1) for the boundedness and asymptotic behavior of solutions.
2. Statement of Results
Our main results are the following theorems.
Theorem 1 Suppose  are continuously differentiable on
are continuously differentiable on ![]() and
and ![]() and the following conditions are satisfied;
and the following conditions are satisfied;
(i)![]() ,
, ![]() for
for![]() ;
;
(ii)![]() ,
, ![]() ,
, ![]() ,
, ![]() for all x, y;
for all x, y;
(iii)![]() ,
, ![]() ,
, ![]() , for all x, y and
, for all x, y and![]() ,
, ![]() ;
;
(iv)![]() , where
, where ![]() is a small positive constant whose magnitude depends only on the constants appeared in (i)-(iii).
is a small positive constant whose magnitude depends only on the constants appeared in (i)-(iii).
Then, every solution ![]() of (1.1) is asymptotically stable and satisfies
of (1.1) is asymptotically stable and satisfies
![]() ,
, ![]() ,
, ![]() as
as![]() .
.
Theorem 2 Let all the conditions of Theorem 1 be satisfied, and in addition we assume that there exist a finite constant ![]() and a non-negative and continuous function
and a non-negative and continuous function ![]() such that p satisfies
such that p satisfies
(i)![]() ,
,
where ![]() for all
for all![]() .
.
Then every solution![]() , of (1.1) satisfies
, of (1.1) satisfies
![]() (2.1)
(2.1)
for all sufficiently large t, while D is a finite constant.
Remark 2.1 Our results develop Qian [13] , Omeike [14] and Tunc’s [15] results to the non-autonomous of the form (1.1).
It is convenient here to consider, the equivalent system of (1.1);
![]()
![]()
![]() (2.2)
(2.2)
and show that under the conditions stated in the theorem, every solution ![]() of (2.2) satisfies
of (2.2) satisfies
![]() (2.3)
(2.3)
for all sufficiently large t, where D is the constant in (2.1).
Our proof of (2.3) rests entirely on the lemma stated below and the scalar function ![]() defined by
defined by
![]() (2.4)
(2.4)
and![]() , an arbitrary fixed constant such that
, an arbitrary fixed constant such that
![]() (2.5)
(2.5)
Lemma 1 Subject to the conditions of Theorem 1 there are positive constants ![]() and
and ![]() depending only on
depending only on![]() , and
, and ![]() such that
such that
![]() (2.6)
(2.6)
Furthermore, there are finite constants ![]() dependent only
dependent only ![]() and
and ![]() such that any solution
such that any solution ![]() of (2.2),
of (2.2),
![]() (2.7)
(2.7)
provided that![]() .
.
Proof: To verify (2.6) observe first that the expressions ![]() in (2.4) may be re-arranged in the form,
in (2.4) may be re-arranged in the form,
![]() (2.8)
(2.8)
By conditions (ii) of Theorem 1 and![]() , we have that the term
, we have that the term
![]()
in the re-arrangement of 2V becomes
![]()
Since![]() ,
, ![]() and
and![]() , (i) of Theorem 1 and combining all these with (2.8), we have
, (i) of Theorem 1 and combining all these with (2.8), we have
![]()
for all x, y and z. Since ![]() satisfy (2.5) and
satisfy (2.5) and![]() , the constants
, the constants ![]() and
and ![]() are positive. This implies that there exists a constant small enough such that
are positive. This implies that there exists a constant small enough such that
![]()
we have
![]() (2.9)
(2.9)
Next, we prove the inequality (2.7). Along any solution ![]() of (2.2), we have
of (2.2), we have
![]()
We easily see that by hypothesis (ii) of Theorem 1,
![]()
![]()
and
![]()
By hypothesis (iii)
![]()
![]()
Also,
![]()
Thus,
![]()
that is,
![]() (2.10)
(2.10)
where ![]() and
and ![]() are constants.
are constants.
Using the inequality (2.6) for all ![]() and
and![]() , we have that
, we have that
![]()
Thus,
![]()
let
![]()
Just as in (2.7), we obtain
![]()
Proof of Theorem 1: It follows that ![]() if and only if
if and only if![]() .
.
Thus, in view of (2.9) and (2.10) and the last discussion, it shows that the trivial solution of (1.1) is asymptotically stable.
Hence, the proof of Theorem 1 is complete.
Proof of Theorem 2: The proof of Theorem 2 depends on the scalar differentiable Lyapunov function ![]() defined in (2.4).
defined in (2.4).
For![]() ,
,
![]()
Since ![]() in (2.11) for all
in (2.11) for all ![]() thus
thus
![]()
Hence, it follows that
![]()
for a constant![]() , where
, where![]() .
.
Making use of the inequalities ![]() and
and![]() . It is clear that
. It is clear that
![]()
by (2.6), we have![]() .
.
Hence,
![]()
or
![]()
We integrate both sides of this inequality from 0 to t and using Gronwall-Bellman inequality, we obtain
![]()
where ![]() is a constant and
is a constant and![]() .
.
Now, since the right-hand side is a constant and since ![]() as
as![]() , it follows that there exist a constant
, it follows that there exist a constant ![]() such that
such that
![]()
From the system (1.1), this implies that
![]()
The proof of Theorem 2 is now complete.
3. Conclusions
The solutions of the third-order non-autonomous nonlinear system are bounded and asymptotically stable according to the Lyapunov’s theory if the inequality (2.5) is satisfied.
Example 2.1 We consider a certain third order non-autonomous scalar differential equation of the form
![]() (3.1)
(3.1)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Choosing![]() , then,
, then, ![]() and
and![]() .
.
Thus,
![]()
and finally,
![]()
and
![]()
Thus, all conditions of the Theorems are satisfied. Therefore, all solutions of (3.1) are asymptotically stable and bounded.