Fixed Point Theorem and Fractional Differential Equations with Multiple Delays Related with Chaos Neuron Models ()
Received 9 July 2015; accepted 27 November 2015; published 30 November 2015


1. Introduction
The following was the famous fixed point theorem introduced by Banach in 1922.
The Banach contraction principle ([1] ). Let 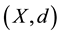 be a complete metric space, let F be a nonempty closed subset of X and let A be a mapping from F into itself. Suppose that there exist
be a complete metric space, let F be a nonempty closed subset of X and let A be a mapping from F into itself. Suppose that there exist  such that
such that
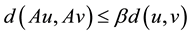
for any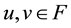 . Then A has a unique fixed point in F.
. Then A has a unique fixed point in F.
In 1999 Lou proved the following fixed point theorem.
Lou’s fixed point theorem ([2] ). Let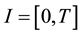 , let
, let 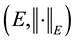 be a Banach space, let
be a Banach space, let 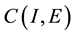 be the Ba- nach space consisting of all continuous mappings from I into E with norm
be the Ba- nach space consisting of all continuous mappings from I into E with norm

for any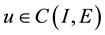 , let F be a nonempty closed subset of
, let F be a nonempty closed subset of 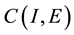 and let A be a mapping from F into itself. Suppose that there exist
and let A be a mapping from F into itself. Suppose that there exist  and
and  such that
such that
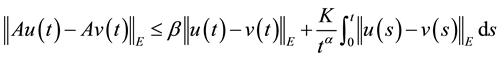
for any 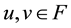 and for any
and for any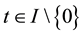 . Then A has a unique fixed point in F.
. Then A has a unique fixed point in F.
Moreover, in 2002 de Pascale and de Pascale proved the following fixed point theorem.
De Pascale-de Pascale’s fixed point theorem ( [3] ). Let![]() , let
, let ![]() be a Banach space, let
be a Banach space, let ![]() be the Banach space consisting of all bounded continuous mappings from I into E with norm
be the Banach space consisting of all bounded continuous mappings from I into E with norm
![]()
for any![]() , let F be a nonempty closed subset of
, let F be a nonempty closed subset of ![]() and let A be a mapping from F into itself. Suppose that there exist
and let A be a mapping from F into itself. Suppose that there exist![]() ,
, ![]() and
and ![]() such that
such that
![]()
for any ![]() and for any
and for any![]() . Then A has a unique fixed point in F.
. Then A has a unique fixed point in F.
In this paper, using the Banach contraction principle, we show a fixed point theorem which deduces to both of Lou’s fixed point theorem and de Pascale and de Pascale’s fixed point theorem. Moreover, our results can be applied to show the existence and uniqueness of solutions for fractional differential equations with multiple delays. Using the theorem, we discuss the fractional chaos neuron model [4] .
2. Fixed Point Theorem
In this section, we show a fixed point theorem. It deduces to Lou’s fixed point theorem [2] and de Pascale and de Pascale’s fixed point theorem [3] .
Definition 1. Let I be an arbitrary finite or infinite interval, let J be an interval with![]() , let
, let ![]() be a Banach space, let
be a Banach space, let ![]() be the Banach space consisting all bounded continuous mappings from I into E with norm
be the Banach space consisting all bounded continuous mappings from I into E with norm
![]()
for any![]() , let
, let ![]() be the Banach space consisting all bounded continuous mappings from J into E with norm
be the Banach space consisting all bounded continuous mappings from J into E with norm
![]()
for any![]() , let F be a nonempty closed subset of
, let F be a nonempty closed subset of![]() , and let
, and let ![]() be a mapping from
be a mapping from ![]() into E. Define a mapping
into E. Define a mapping ![]() by
by
![]()
for any![]() . We say F satisfies (*) for
. We say F satisfies (*) for ![]() if (*)
if (*)![]() holds for any
holds for any![]() .
.
Theorem 1. Let I be an arbitrary finite or infinite interval, let ![]() be intervals with
be intervals with![]() , let
, let ![]() be a Banach space, let
be a Banach space, let ![]() be the Banach space consisting all bounded continuous mappings from I into E with norm
be the Banach space consisting all bounded continuous mappings from I into E with norm
![]()
for any![]() , and let F be a nonempty closed subset of
, and let F be a nonempty closed subset of![]() . Suppose that there exists a mapping
. Suppose that there exists a mapping ![]() from
from ![]() into E such that F satisfies (*) for
into E such that F satisfies (*) for![]() . Let A be a mapping from F into itself. Suppose that there exist
. Let A be a mapping from F into itself. Suppose that there exist![]() , a mapping G from
, a mapping G from ![]() into
into ![]() integrable with respect to the second variable for any the first variable, mappings
integrable with respect to the second variable for any the first variable, mappings ![]() from I into
from I into ![]() with
with![]() ,
, ![]() , and mappings
, and mappings ![]() for any
for any ![]() such that
such that
(H1) for any ![]() and for any
and for any ![]()
![]()
(H2) there exist![]() ,
, ![]() ,
, ![]() with
with ![]() and
and ![]() such that
such that
1)![]() ;
;
2) ![]() for any
for any ![]() and for any
and for any![]() ;
;
3) ![]() for any
for any![]() .
.
Then A has a unique fixed point in F.
Proof. By (H1) we obtain
![]()
for any ![]() and for any
and for any![]() . By (H2) there exists
. By (H2) there exists![]() , that is,
, that is, ![]() for any
for any![]() . Define a new norm
. Define a new norm ![]() in
in ![]() by
by
![]()
Since
![]()
![]() is equivalent of
is equivalent of![]() . Define a metric d in F by
. Define a metric d in F by
![]()
Since ![]() for any
for any![]() , we obtain
, we obtain
![]()
and hence ![]() is a complete metric space. We obtain
is a complete metric space. We obtain
![]()
for any ![]() and for any
and for any![]() . Since
. Since ![]() for any
for any![]() , we obtain
, we obtain
![]()
that is, A is a contraction mapping. By the Banach contraction principle A has a unique fixed point in F.
The following remarks show that our fixed point theorem derives Lou’s fixed point theorem [2] and de Pascale and de Pascale’s fixed point theorem [3] . The proofs are owed to [5] .
Remark 1. By Theorem 1 we can obtain Lou’s fixed point theorem [2] . Actually let![]() , let
, let ![]() be a Banach space, let
be a Banach space, let ![]() be the Banach space consisting of all continuous mappings from I into E with norm
be the Banach space consisting of all continuous mappings from I into E with norm
![]()
for any![]() , and let F be a nonempty closed subset of
, and let F be a nonempty closed subset of![]() . F satisfies (*) for the null mapping. Note that, since I is a finite interval,
. F satisfies (*) for the null mapping. Note that, since I is a finite interval, ![]() is equivalent to
is equivalent to![]() . Let A be a mapping from F into itself. Suppose that there exist
. Let A be a mapping from F into itself. Suppose that there exist ![]() and
and ![]() such that
such that
![]()
for any ![]() and for any
and for any![]() . Note that A is continuous. Therefore by the l’Hopital theorem we obtain
. Note that A is continuous. Therefore by the l’Hopital theorem we obtain
![]()
for any![]() . Put
. Put
![]()
![]() ,
, ![]() ,
, ![]() and
and![]() . Then we obtain
. Then we obtain
![]()
for any ![]() and for any
and for any![]() , that is, (H1) holds. Take
, that is, (H1) holds. Take ![]() satisfying
satisfying![]() . Put
. Put
![]() ,
,![]() ,
,![]() , and
, and![]()
![]()
Then (1) and (2) of (H2) hold. Moreover, if![]() , then
, then
![]()
if![]() , then
, then
![]()
that is, (3) of (H2) holds. Therefore, by Theorem 1 A has a unique fixed point in F.
Remark 2. By Theorem 1 we can obtain de Pascale and de Pascale’s fixed point theorem [3] . Actually let![]() , let
, let ![]() be a Banach space, let
be a Banach space, let ![]() be the Banach space consisting of all bounded continuous mappings from I into E with norm
be the Banach space consisting of all bounded continuous mappings from I into E with norm
![]()
for any![]() , and let F be a nonempty closed subset of
, and let F be a nonempty closed subset of![]() . F satisfies (*) for the null mapping. Let A be a mapping from F into itself. Suppose that there exist
. F satisfies (*) for the null mapping. Let A be a mapping from F into itself. Suppose that there exist![]() ,
, ![]() and
and ![]() such that
such that
![]()
for any ![]() and for any
and for any![]() . Put
. Put
![]()
![]() ,
, ![]() ,
, ![]() and
and![]() . Then we obtain
. Then we obtain
![]()
for any ![]() and for any
and for any![]() , that is, (H1) holds. Take
, that is, (H1) holds. Take ![]() and
and ![]() satisfying
satisfying ![]() . Put
. Put![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and
![]()
Then (1) and (2) of (H2) hold. Moreover, if![]() , then
, then
![]()
if![]() , then
, then
![]()
that is, (3) of (H2) holds. Therefore, by Theorem 1 A has a unique fixed point in F.
3. Fractional Differential Equations with Multiple Delays
In this section, by using Theorem 1, we show the existence and uniqueness of solutions for fractional differential equations with multiple delays. Throughout this paper, the fractional derivative means the Caputo-Riesz derivative ![]() defined by
defined by
![]()
for any ![]() and for any function u, where
and for any function u, where ![]() is the gamma function and m is a natural number with
is the gamma function and m is a natural number with![]() ; for instance, see [6] .
; for instance, see [6] .
Theorem 2. Let ![]() be a Banach space, let
be a Banach space, let ![]() be the space consisting of all continu-
be the space consisting of all continu-
ous mappings from ![]() into E and let
into E and let ![]() satisfying
satisfying
(Hf) there exist ![]() such that
such that
![]()
for any ![]() and for any
and for any![]() .
.
Let ![]() be the Banach space consisting of all continuous mappings from
be the Banach space consisting of all continuous mappings from ![]() into E, let
into E, let
![]() be the space consisting of all continuous mappings from
be the space consisting of all continuous mappings from ![]() into
into ![]() and let
and let
![]() be the space consisting of all continuous mappings from
be the space consisting of all continuous mappings from ![]() into E. Then the following fractional differential equation with multiple delays
into E. Then the following fractional differential equation with multiple delays
![]()
where![]() ,
, ![]() is the
is the ![]() -order Caputo-Riesz derivative,
-order Caputo-Riesz derivative, ![]() and
and![]() ,
,
have a unique solution in![]() .
.
Proof. Put![]() ,
, ![]() ,
, ![]() and
and
![]()
Then F is closed. Since ![]() and
and ![]() for any
for any![]() , we obtain
, we obtain ![]() for any
for any![]() . Therefore, F satisfies (*) for
. Therefore, F satisfies (*) for![]() . By direct computations,
. By direct computations, ![]() is a solution of the equation above if and only if it is a solution of the following integral equation:
is a solution of the equation above if and only if it is a solution of the following integral equation:
![]()
Define a mapping A by
![]()
for any![]() . Since
. Since![]() , we obtain
, we obtain![]() . We show that A has a unique fixed point. Indeed, we obtain
. We show that A has a unique fixed point. Indeed, we obtain
![]()
where![]() ,
, ![]() and
and![]() . Put
. Put![]() ,
,
![]()
![]() and
and![]() . Then (H1) holds. Take
. Then (H1) holds. Take ![]() with
with ![]() and take c with
and take c with![]() . Put
. Put![]() ,
,
![]() ,
, ![]() and
and![]() . Then (1) and (2) of (H2) hold. Moreover, since
. Then (1) and (2) of (H2) hold. Moreover, since
![]()
(3) of (H2) holds. Therefore, by Theorem 1 A has a unique fixed point in F.
By using Theorem 2, we discuss the fractional chaos neuron model [4] .
Example 1. We consider the following fractional differential equation with delay
![]()
where![]() ,
, ![]() ,
, ![]() and
and![]() . In this equation,
. In this equation, ![]() is an internal state of the neuron at time t,
is an internal state of the neuron at time t, ![]() is a dissipative parameter and
is a dissipative parameter and ![]() is delay time. Moreover, we use a sinusoidal function with a periodic parameter
is delay time. Moreover, we use a sinusoidal function with a periodic parameter ![]() as an activation to be related to the output of the neuron. This equation is
as an activation to be related to the output of the neuron. This equation is
called the fractional chaos neuron model [4] . Put![]() ,
, ![]() ,
, ![]() and
and![]() .
.
Since
![]()
f satisfies (Hf) for ![]() and
and![]() . Therefore, by Theorem 2 the equation above has a unique solution in
. Therefore, by Theorem 2 the equation above has a unique solution in
![]() . For analysis of neural networks using fixed point theorems, see [7] [8] .
. For analysis of neural networks using fixed point theorems, see [7] [8] .
Acknowledgements
The authors would like to thank the referee for valuable comments.