Positive Solutions for Systems of Coupled Fractional Boundary Value Problems ()
1. Introduction
Fractional differential equations describe many phenomena in various fields of engineering and scientific dis- ciplines such as physics, biophysics, chemistry, biology (such as blood flow phenomena), economics, control theory, signal and image processing, aerodynamics, viscoelasticity, electromagnetics, and so on (see [1] -[6] ). For some recent developments on the topic, which can be seen in [7] - [19] and the references therein.
In this paper, we consider the system of nonlinear ordinary fractional differential equations
(S) 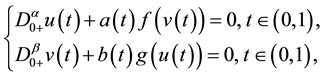
with the coupled integral boundary conditions
(BC) 
where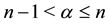 ,
, 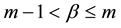 ,
, 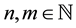 ,
, 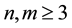 ,
,  and
and 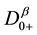 denote the Riemann-Liouville derivatives of orders
denote the Riemann-Liouville derivatives of orders 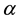 and
and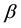 , respectively, the integrals from (BC) are Riemann-Stieltjes integrals,
, respectively, the integrals from (BC) are Riemann-Stieltjes integrals, 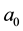 and
and 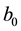 are positive constants.
are positive constants.
Under some assumptions on the functions f and g, we shall prove the existence of positive solutions of problem (S)-(BC). By a positive solution of (S)-(BC), we mean a pair of functions 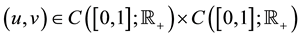 satisfying (S) and (BC) with
satisfying (S) and (BC) with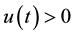 ,
, 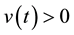 for all
for all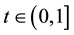 . We shall also give sufficient conditions for
. We shall also give sufficient conditions for
the nonexistence of positive solutions for this problem. Some systems of fractional equations with parameters subject to coupled integral boundary conditions were studied in [20] by using the Guo-Krasnosel’skii fixed point theorem. We also mentioned the paper [21] , where we investigated the existence and multiplicity of positive
solutions for the system![]() ,
, ![]() , with the integral boundary conditions (BC) with
, with the integral boundary conditions (BC) with ![]() by using some theorems from the fixed point index theory and the
by using some theorems from the fixed point index theory and the
Guo-Krasnosel’skii fixed point theorem. In [21] , the nonlinearities f and g may be nonsingular or singular in ![]() and/or
and/or![]() . Some systems of Riemann-Liouville fractional equations with or without parameters subject to uncoupled boundary conditions are studied in the papers [22] - [25] , and the book [26] .
. Some systems of Riemann-Liouville fractional equations with or without parameters subject to uncoupled boundary conditions are studied in the papers [22] - [25] , and the book [26] .
In Section 2, we present some auxiliary results which investigate a system of Riemann-Liouville fractional equations subject to coupled integral boundary conditions. In Section 3, we prove our main results, and an example which supports the obtained results is finally presented in Section 4. In the proof of our existence result, we shall use the Schauder fixed point theorem which we present now.
Theorem 1. Let X be a Banach space and ![]() a nonempty, bounded, convex and closed subset. If the operator
a nonempty, bounded, convex and closed subset. If the operator ![]() is completely continuous, then A has at least one fixed point.
is completely continuous, then A has at least one fixed point.
2. Auxiliary Results
We present here the definitions of the fractional integral and Riemann-Liouville fractional derivative of a function, and some auxiliary results from [20] and [22] that will be used to prove our main theorems.
Definition 2.1: The (left-sided) fractional integral of order ![]() of a function
of a function ![]() is given by
is given by
![]()
provided the right-hand side is pointwise defined on![]() , where
, where ![]() is the Euler gamma function defined by
is the Euler gamma function defined by![]() ,
,![]() .
.
Definition 2.2: The Riemann-Liouville fractional derivative of order ![]() for a function
for a function ![]() is given by
is given by
![]()
where![]() , provided that the right-hand side is pointwise defined on
, provided that the right-hand side is pointwise defined on![]() .
.
The notation ![]() stands for the largest integer not greater than
stands for the largest integer not greater than![]() . If
. If ![]() then
then ![]() for
for![]() , and if
, and if ![]() then
then ![]() for
for![]() .
.
We consider now the fractional differential system
![]() (1)
(1)
with the coupled integral boundary conditions
![]() (2)
(2)
where![]() ,
, ![]() and
and ![]() are functions of bounded variation.
are functions of bounded variation.
Lemma 1. ( [20] ) If ![]() are functions of bounded variations,
are functions of bounded variations, ![]() and
and![]() , then the unique solution of problem (1)-(2) is given by
, then the unique solution of problem (1)-(2) is given by
![]() (3)
(3)
where
![]() (4)
(4)
and
![]() (5)
(5)
Lemma 2. ( [22] ) The functions ![]() and
and ![]() given by (5) have the properties
given by (5) have the properties
a) ![]() are continuous functions and
are continuous functions and![]() ,
, ![]() for all
for all ![]() ;
;
b)![]() , for all
, for all![]() ;
;
c) For any![]() , we have
, we have
![]()
for all![]() , where
, where![]() ,
, ![]() ,
, ![]() and
and ![]()
Lemma 3. ( [20] ) If ![]() are nondecreasing functions, and
are nondecreasing functions, and![]() , then
, then![]() ,
, ![]() given by (4) are continuous functions on
given by (4) are continuous functions on ![]() and satisfy
and satisfy ![]() for all
for all![]() ,
,![]() . Moreover, if
. Moreover, if ![]() satisfy
satisfy![]() ,
, ![]() for all
for all![]() , then the solution
, then the solution ![]() of problem (1)-(2) satisfies
of problem (1)-(2) satisfies ![]() for all
for all![]() .
.
Lemma 4. ( [20] ) Assume that ![]() are nondecreasing functions and
are nondecreasing functions and![]() . Then the functions
. Then the functions ![]() satisfy the inequalities
satisfy the inequalities
a1)![]() , where
, where
![]()
a2) For every![]() , we have
, we have
![]()
b1)![]() , where
, where ![]()
b2) For every![]() , we have
, we have
![]()
c1)![]() , where
, where
![]()
c2) For every![]() , we have
, we have
![]()
d1)![]() , where
, where ![]()
d2) For every![]() , we have
, we have
![]()
Lemma 5. ( [20] ) Assume that ![]() are nondecreasing functions,
are nondecreasing functions, ![]() ,
, ![]() and
and![]() ,
, ![]() ,
, ![]() for all
for all![]() . Then the solution
. Then the solution![]() ,
, ![]() of problem (1)-(2) (given by (3)) satisfies the inequalities
of problem (1)-(2) (given by (3)) satisfies the inequalities
![]()
3. Main Results
We present first the assumptions that we shall use in the sequel.
(J1) ![]() are nondecreasing functions and
are nondecreasing functions and![]() .
.
(J2) The functions ![]() are continuous and there exist
are continuous and there exist ![]() such that
such that![]() ,
,![]() .
.
(J3) ![]() are continuous functions and there exists
are continuous functions and there exists ![]() such that
such that
![]() ,
, ![]() for all
for all![]() ,
,
where ![]() and
and ![]() are de- fined in Lemma 4.
are de- fined in Lemma 4.
(J4) are continuous functions and satisfy the conditions
![]()
By assumption (J2) we deduce that![]() ,
, ![]() ,
, ![]() and
and ![]() , that is, the constant L from (J3) is positive.
, that is, the constant L from (J3) is positive.
Our first theorem is the following existence result for problem (S)-(BC).
Theorem 2. Assume that assumptions (J1)-(J3) hold. Then problem (S)-(BC) has at least one positive solution for ![]() and
and ![]() sufficiently small.
sufficiently small.
Proof. We consider the system of ordinary fractional differential equations
![]() (6)
(6)
with the coupled integral boundary conditions
![]() (7)
(7)
with ![]() and
and![]() .
.
The above problem (6)-(7) has the solution
![]() (8)
(8)
where ![]() is defined in (J1). By assumption (J1) we obtain
is defined in (J1). By assumption (J1) we obtain ![]() and
and ![]() for all
for all![]() .
.
We define the functions ![]() and
and![]() ,
, ![]() by
by
![]()
where ![]() is a solution of (S)-(BC). Then (S)-(BC) can be equivalently written as
is a solution of (S)-(BC). Then (S)-(BC) can be equivalently written as
![]() (9)
(9)
with the boundary conditions
![]() (10)
(10)
Using the Green’s functions![]() ,
, ![]() from Lemma 1, a pair
from Lemma 1, a pair ![]() is a solution of problem (9)-(10) if and only if
is a solution of problem (9)-(10) if and only if ![]() is a solution for the nonlinear integral equations
is a solution for the nonlinear integral equations
![]() (11)
(11)
where ![]() and
and![]() ,
, ![]() are given in (8).
are given in (8).
We consider the Banach space ![]() with the supremum norm
with the supremum norm![]() , the space
, the space ![]() with the norm
with the norm![]() , and we define the set
, and we define the set
![]()
We also define the operators ![]() and
and ![]() by
by
![]()
for all![]() , and
, and![]() .
.
For sufficiently small ![]() and
and![]() , by (J3), we deduce
, by (J3), we deduce
![]()
Then, by using Lemma 3, we obtain![]() ,
, ![]() for all
for all ![]() and
and![]() . By Lemma 4, for all
. By Lemma 4, for all![]() , we have
, we have
![]()
and
![]()
Therefore![]() .
.
Using standard arguments, we deduce that S is completely continuous. By Theorem 1, we conclude that S has a fixed point![]() , which represents a solution for problem (9)-(10). This shows that our problem (S)-(BC) has a positive solution
, which represents a solution for problem (9)-(10). This shows that our problem (S)-(BC) has a positive solution ![]() with
with ![]() for sufficiently small
for sufficiently small ![]() and
and![]() .
.
In what follows, we present sufficient conditions for the nonexistence of positive solutions of (S)-(BC).
Theorem 3. Assume that assumptions (J1), (J2) and (J4) hold. Then problem (S)-(BC) has no positive solution for ![]() and
and ![]() sufficiently large.
sufficiently large.
Proof. We suppose that ![]() is a positive solution of (S)-(BC). Then
is a positive solution of (S)-(BC). Then ![]() with
with![]() ,
, ![]() is a solution for problem (9)-(10), where
is a solution for problem (9)-(10), where ![]() is the solution of problem (6)-(7) (given by (8)). By (J2) there exists
is the solution of problem (6)-(7) (given by (8)). By (J2) there exists ![]() such that
such that![]() , and then
, and then![]() ,
, ![]() ,
, ![]() ,
,![]() . Now by using Lemma 3, we have
. Now by using Lemma 3, we have![]() ,
, ![]() for all
for all![]() , and by Lemma 5 we obtain
, and by Lemma 5 we obtain ![]() and
and![]() .
.
Using now (8), we deduce that ![]() and
and![]() . Therefore, we obtain
. Therefore, we obtain ![]() and
and![]() .
.
We now consider![]() . By using (J4), for R defined above, we conclude that there exists
. By using (J4), for R defined above, we conclude that there exists ![]() such that
such that![]() ,
, ![]() for all
for all![]() . We consider
. We consider ![]() and
and ![]() sufficiently large such that
sufficiently large such that ![]() and
and![]() . By (J2), (9), (10) and the above inequalities, we deduce that
. By (J2), (9), (10) and the above inequalities, we deduce that ![]() and
and![]() .
.
Now by using Lemma 4 and the above considerations, we have
![]()
Therefore, we obtain![]() , which is a contradiction, because
, which is a contradiction, because![]() . Then, for
. Then, for ![]() and
and ![]() sufficiently large, our problem (S)-(BC) has no positive solution.
sufficiently large, our problem (S)-(BC) has no positive solution.
4. An Example
We consider![]() ,
, ![]() for all
for all![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]() , for all
, for all![]() ,
, ![]() then
then ![]() and
and![]() . We also consider the functions
. We also consider the functions![]() ,
, ![]() ,
, ![]() , for all
, for all![]() , with
, with![]() . We have
. We have![]() .
.
Therefore, we consider the system of fractional differential equations
(S0) ![]()
with the boundary conditions
(BC0) ![]()
Then we obtain
![]()
We also deduce
![]()
![]() ,
, ![]() for all
for all![]() . For the functions
. For the functions![]() ,
, ![]() , we obtain
, we obtain
![]()
![]()
![]()
![]()
Then we deduce that assumptions (J1), (J2) and (J4) are satisfied. In addition, by using the above functions![]() ,
, ![]() , we obtain
, we obtain![]() ,
, ![]() ,
,
![]() ,
, ![]() , and then
, and then![]() . We choose
. We choose ![]() and if we select
and if we select![]() , then we conclude that
, then we conclude that![]() ,
, ![]() for all
for all![]() . For example, if
. For example, if ![]() and
and![]() , then the above conditions for f and g are satisfied. So,
, then the above conditions for f and g are satisfied. So,
assumption (J3) is also satisfied. By Theorems 2 and 3 we deduce that problem (S0)-(BC0) has at least one positive solution for sufficiently small ![]() and
and![]() , and no positive solution for sufficiently large
, and no positive solution for sufficiently large ![]() and
and![]() .
.
Acknowledgements
The work of R. Luca and A. Tudorache was supported by a grant of the Romanian National Authority for Scientific Research, CNCS-UEFISCDI, project number PN-II-ID-PCE-2011-3-0557.