Effects of a Periodic Decay Rate on the Statistics of Radioactive Decay: New Methods to Search for Violations of the Law of Radioactive Change ()
1. Introduction
1.1. Violations of the Radioactive Decay Law
Radioactivity refers to the spontaneous transformation of one kind of atomic nucleus (designated a “nuclide” in the terminology of nuclear physics) into a different kind of atomic nucleus, ordinarily with the emission of a helium-4 nucleus (alpha particle), fast electron or positron (beta particle), high-energy electromagnetic radiation (gamma photon) or, more rarely, some other particle or cluster [1] . In a sample initially comprising N0 radioactive nuclei, the number surviving after a time interval t is given by the exponential survival law―designated the Law of Radioactive Change by Rutherford and Soddy [2]
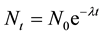 (1)
(1)
with decay rate parameter λ.
The salient feature of standard radioactive decay, irrespective of the particular process by which the transmutation of nuclear identity occurs, was described by Rutherford and Soddy in 1903 [2] .
“The radioactive constant λ has been investigated under very widely varied conditions of temperature, and under the influence of the most powerful chemical and physical agencies, and no alteration of its value has been observed. The law forms in fact the mathematical expression of a general principle…”
The Law of Radioactive Change and its underlying statistical foundations have been the basis for practical nuclear metrology for more than a century from the discovery of radioactivity up to present times. For example, taking account of the enormous developments in nuclear physics in the years following Rutherford and Soddy’s early discovery, one still finds in influential nuclear science textbooks a confirmation of the same general principle that
“No change in the decay rates of particle emission has been observed over extreme variations of conditions such as temperature, pressure, chemical state, or physical environment.” [3]
Actually, there are a few known physical processes such as electron-capture decay [4] in which the decay rate of a particular radioactive nuclide depends on the electron density near the nucleus and can therefore be affected (usually very weakly) by its chemical environment [5] or (possibly very strongly) by laser-induced ionization [6] . These exceptional processes are reasonably well understood and in conformity with known physical laws. However, during the past 15 years or so, the constancy of the radioactive decay rate has been called into question in other ways apart from these known exceptions on both theoretical and experimental grounds.
With regard to theory, it has in fact been known since the early development of quantum electrodynamics that the exponential decay law is an approximate result that follows from neglect of the energy-dependence of certain terms in the Green’s functions from which the associated decay amplitudes are calculated [7] . The approximation leading to a constant decay rate (as well as to an energy level shift [8] ) is essentially equivalent to the “Fermi golden rule” in first-order perturbation theory. Mathematically, poles of the Green’s functions in the lower half of the second Riemann sheet give rise to exponential decay, whereas the branch line gives rise to corrections to exponential decay [9] . Deviations from exponential decay derivable from quantum theory were predicted to occur for time intervals very short or very long compared with the mean lifetime. Experimental evidence of non-exponential decay in the atomic/molecular domain consistent with quantum theory was first reported in 1997 for quantum tunneling [10] and has since been reported for spontaneous transitions from excited states with emission of optical photons such as in [11] .
However, more recent model-dependent calculations with a focus on the decay of nuclear states have predicted non-exponential behavior at intermediate times as well, including the possibility of oscillatory behavior throughout the entire decay transient [12] -[14] . Moreover, a number of experimental studies, of which [15] -[17] are representative, independently claimed to have observed non-exponential decay of diverse radioactive nuclides, in particular beta emitters. Some of these publications were based on meta analyses of data collected years earlier by scientists at other laboratories, whereas other publications reported the outcomes of contemporaneous experiments. Collectively, the non-standard radioactive decay processes reportedly manifested time-varying decay transients with geophysical or astrophysical periodicities including, for example, diurnal, monthly, seasonal, and annual variations. Several of the experimental papers attributed the alleged effects to novel interactions of a cosmological nature. Among the nuclides claimed to violate the standard radioactive decay law are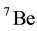 ,
, 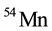 ,
,  ,
,  ,
,  ,
, 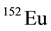 ,
, 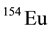 ,
, 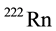 ,
, 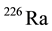 ,
, 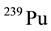 , and perhaps others.
, and perhaps others.
Claims of radioactivity exhibiting periodic decay rates and extra-nuclear environmental correlations are highly controversial, and refutations have been published in specific cases, e.g. [18] -[20] . At present, the issue remains ambiguous but with far-reaching theoretical consequences. If reported phenomena like these turn out to be physically real and not instrumental artifacts, an explanation will almost surely require an extension of the currently known laws of physics.
1.2. Statistical Basis of a New Search Procedure
Experimentally, claims of non-standard radioactive decay have been drawn primarily from perceived deviations from the exponential decay law (1), which follows from a Poisson distribution of decay events as expressed by the probability function
 (2)
(2)
for x decays within a counting interval (bin width) Δt, given a mean count
 . (3)
. (3)
The reported deviations were very weak, typically a few tenths of a per cent.
A much more sensitive method by which to search for a time-dependent nuclear decay rate was recently proposed by Silverman [21] . The method involves examining, not the decay transient itself, but the statistical distribution of decay events―i.e. the sample activity―recorded in a long time series of discrete counts. As shown in [21] , a periodic time dependence in the intrinsic radioactive decay rate can lead to a pattern of maxima and minima in the theoretical probability density function (pdf) and therefore in the corresponding histogram of chronologically recorded experimental activities.
In order to search for non-standard radioactive decay based on the statistical distribution of decay events, it is first necessary to understand better the statistics of standard radioactive decay (i.e. at constant decay rate). In Section 2 of this paper the statistics of a time series of radioactive decays are investigated in greater detail first for standard radioactive decay with constant decay rate λ (mean lifetime ) and second for a variable decay rate
) and second for a variable decay rate 
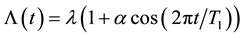 (4)
(4)
with constant decay parameter λ, amplitude![]() , and period T1. The probability density function (pdf) is examined as a function of the initial mean count per bin
, and period T1. The probability density function (pdf) is examined as a function of the initial mean count per bin ![]() (in effect, the strength of the source activity), the duration T of the time series of measurements, and, in the case of non-standard decay, the parameters
(in effect, the strength of the source activity), the duration T of the time series of measurements, and, in the case of non-standard decay, the parameters![]() , T1 of the periodic component of
, T1 of the periodic component of![]() .
.
In Section 3 the effect of a variable nuclear decay rate on a different statistical distribution―the distribution of mean lifetime measurements―is examined and shown to provide another sensitive statistical method by which to search for non-standard radioactive decay. This novel method of determining nuclear half-lives was first discovered empirically [22] and subsequently derived and explained theoretically [23] . For radioactive decay in accord with the Rutherford-Soddy law, the distribution of mean lifetime measurements is a symmetric Cauchy function centered on the true value of the mean lifetime T0, which is related to the half-life ![]() by
by
![]() . (5)
. (5)
For a time-dependent decay rate, however, the distribution is displaced, widened, and no longer of Cauchy form.
In Section 4 the effects of a time-varying decay rate on the power spectrum and autocorrelation function of a time series of nuclear activities are discussed.
Conclusions are summarized in Section 5.
2. Distribution of Nuclear Decay Events
2.1. Radioactivity at Constant Decay Rate λ
The quantitative detection of radioactivity is ordinarily made by counting emitted particles in discrete time windows or bins. (Sometimes the detected signal is an ionization current which, when necessary, can be converted to a particle count per unit time.) In nuclear terminology “activity” ![]() is proportional to the count rate
is proportional to the count rate
![]() , (6)
, (6)
where the constant c denotes the instrumental detection efficiency. The fundamental SI unit of activity is the Becquerel (1 Bq = 1 decay/s). As used in this paper―the primary objective of which is theoretical, i.e. to elucidate the statistics of nuclear decay―the bin width Δt is taken to be 1 time unit (e.g. second, hour, day, etc.), c is taken to be 100%, and the activity xt at discrete time t is therefore a pure number (no units or dimensions) equal to the number of counts in Δt. The temporal index t is an integer denoting the number of unit intervals Δt. Similarly, the total duration TΔt of counting is simply the integer T.
From a statistical perspective the counting of particles emitted from a radioactive source that decays at a constant rate is tantamount to sampling a population of independent Poisson variates of some mean value ![]() given by Equation (3). Each measurement of activity constitutes an independent sample. The activity
given by Equation (3). Each measurement of activity constitutes an independent sample. The activity ![]() at time t is then a random variable symbolized by the expression
at time t is then a random variable symbolized by the expression![]() . In a Poisson distribution the variance
. In a Poisson distribution the variance ![]() equals the mean
equals the mean![]() , where the angular brackets
, where the angular brackets ![]() signify an expectation value. This paper is concerned primarily with the statistics resulting from a high initial activity and long counting time such as employed in many measurements in nuclear metrology [24] . For a Poisson population with mean
signify an expectation value. This paper is concerned primarily with the statistics resulting from a high initial activity and long counting time such as employed in many measurements in nuclear metrology [24] . For a Poisson population with mean![]() , the discrete pdf (2) is very closely approximated by a Gaussian (or normal) pdf
, the discrete pdf (2) is very closely approximated by a Gaussian (or normal) pdf
![]() (7)
(7)
with![]() . A normal variate is symbolized by
. A normal variate is symbolized by![]() . Thus the count xt from a high-activity radioactive source may be represented as a Poisson-Gauss (PG) variate
. Thus the count xt from a high-activity radioactive source may be represented as a Poisson-Gauss (PG) variate![]() .
.
Over a time interval![]() , the T independent samples
, the T independent samples ![]()
![]() are all, to good approximation, variates from the same Poisson population. However, when the total duration T of counting extends over a substantial part of one or more half-lives, the activity measurements are no longer from the same Poisson population because the mean count per bin
are all, to good approximation, variates from the same Poisson population. However, when the total duration T of counting extends over a substantial part of one or more half-lives, the activity measurements are no longer from the same Poisson population because the mean count per bin ![]() is decreasing in time. The time series of samples
is decreasing in time. The time series of samples ![]() constitute a “mixed distribution” (also referred to in the statistical literature as a “contagious distribution” [25] ). The normalized pdf of the mixed Poisson-Gauss (MPG) distribution describing radioactive decay with constant decay parameter takes the form [21]
constitute a “mixed distribution” (also referred to in the statistical literature as a “contagious distribution” [25] ). The normalized pdf of the mixed Poisson-Gauss (MPG) distribution describing radioactive decay with constant decay parameter takes the form [21]
![]() (8)
(8)
with ![]() from Equation (3), or, equivalently,
from Equation (3), or, equivalently,
![]() (9)
(9)
under a transformation
![]() (10)
(10)
to the dimensionless variate ![]() whose range,
whose range, ![]() , is narrower and more convenient compared with
, is narrower and more convenient compared with ![]() (since
(since![]() ). Note that the practical upper limit to the range is approximate because x (and therefore z) are random variables. Thus, although
). Note that the practical upper limit to the range is approximate because x (and therefore z) are random variables. Thus, although![]() , an individual sample xt at any time t could exceed
, an individual sample xt at any time t could exceed![]() .
.
In marked contrast to the pictorial representations of Poisson distributions frequently seen in nuclear science textbooks as well as in the research literature, the true pdf (8) or (9) of a long time series of radioactive decays bears no resemblance to a Poisson distribution. Figure 1 shows the variation in form of pdf (9) for radioactive decay with lifetime T0 = 100 and initial mean activity (A) μ0 = 100 or (B) μ0 = 1000 as the number of samples comprising the time series increases from T = 1 (plot a) to T = 450 (plot g). Plot a is the distribution that would result from drawing numerous samples all from a pure Poisson population of initial mean activity μ0. However, in a time series of radioactive decay measurements, ordinarily only the first measurement is drawn from distribution a, and each subsequent measurement is drawn from a residual population of lower mean activity. As the number of measurements increases and the residual mean activity decreases, the pdf of the distribution skews markedly to the left―i.e. in the direction of decreasing μt.
Although there is no closed form for the mixed Poisson-Gauss pdfs (8) or (9), a very accurate expression can be derived for ![]() by approximating the sum in (8) by the integral
by approximating the sum in (8) by the integral
![]() (11)
(11)
(since the sum extends over all integer values of t from 0 to ![]() in unit intervals
in unit intervals![]() ), and then transforming the integration variable by
), and then transforming the integration variable by ![]() to obtain
to obtain
![]() , (12)
, (12)
which reduces to a x−1 power-law in the long-time limit. The exact calculations (solid curves) of pdf (9) in Figure 1(A) and Figure 1(B) are identically color coded according to duration of sampling T. Superposed on the exact plots of 1A, however, are the values (dotted black curves) obtained from the integral approximation (12). The visually perfect overlap illustrates how closely the integral expression (12) approximates the exact expression (9). (For easier color identification, the superposed black plots of pdf (12) were omitted from Figure 1(B), but the approximate and exact plots overlapped just as closely as in Figure 1(A)). With increasing T, the plots in Figure 1 (e.g. plots e, f, g) increasingly manifest the long tail of the x−1 power law (12) before plunging to 0 at x = 0. It is interesting to note that the integrand in Equation (12) has the form (to within a normalization constant) of an Inverse Gaussian (also known as a Wald) distribution, which arises in the analysis of Brownian diffusion processes [26] .
In comparing corresponding plots (i.e. of the same color) in Figure 1(A) and Figure 1(B), it is to be noted that the pure Poisson distribution a (red) of mean activity μ0 = 1000 is narrower than Poisson distribution a (red)
![]()
Figure 1. Variation of probability density ![]() (solid curves) and integral approximation
(solid curves) and integral approximation ![]() (dotted curves) as a function of normalized activity
(dotted curves) as a function of normalized activity ![]() for initial mean activity (A) μ0 = 100, (B) μ0 = 1000, lifetime T0 = 100, and time series duration (i.e. number of samples, each from an independent Poisson distribution) T = (a) 1 (red), (b) 50 (blue), (c) 100 (green), (d) 200 (orange), (e) 300 (violet), (f) 400 (cyan), (g) 450 (black). T0 and T are in units of sampling time Δt.
for initial mean activity (A) μ0 = 100, (B) μ0 = 1000, lifetime T0 = 100, and time series duration (i.e. number of samples, each from an independent Poisson distribution) T = (a) 1 (red), (b) 50 (blue), (c) 100 (green), (d) 200 (orange), (e) 300 (violet), (f) 400 (cyan), (g) 450 (black). T0 and T are in units of sampling time Δt.
defined by μ0 = 100, in contrast to what one might expect, since the variance of a Poisson distribution equals the mean μ0. The explanation is that the distributed variate in the figure is not x but![]() . The maximum and width of pdf (9) are respectively
. The maximum and width of pdf (9) are respectively![]() ,
, ![]() , and therefore the ratio
, and therefore the ratio![]() . The sharpness of a PG distribution in z, therefore, increases with the initial mean activity μ0. Apart from the two Poisson plots a, an examination of the other corresponding plots in Figure 1(A) and Figure 1(B) suggests that, all other parameters remaining fixed, a higher initial activity leads to a more skewed pdf with flatter peaks and steeper rise and decline. This observation is basically true, but will be formulated more quantitatively, when the moments of the distribution are calculated.
. The sharpness of a PG distribution in z, therefore, increases with the initial mean activity μ0. Apart from the two Poisson plots a, an examination of the other corresponding plots in Figure 1(A) and Figure 1(B) suggests that, all other parameters remaining fixed, a higher initial activity leads to a more skewed pdf with flatter peaks and steeper rise and decline. This observation is basically true, but will be formulated more quantitatively, when the moments of the distribution are calculated.
Figure 2 shows the variation in MPG probability density for a fixed total counting time T as the initial source activity increases from μ0 = 102 (red) to μ0 = 105 (orange). The higher the value of μ0, the more sharply the pdf sides drop to the horizontal baseline, as indicated in Figure 1. The gray curve traces the pdf (12) in the power law limit. The increasingly sharp drop in the sides of the MPG pdf with increasing mean initial activity is attributable entirely to the Gaussian exponent in relations (8) or (9). In the limit of a very high value of μ0, the func-
tion ![]() acts like a Dirac delta function, dropping rapidly to zero at all values of z ex-
acts like a Dirac delta function, dropping rapidly to zero at all values of z ex-
cept in the immediate vicinity of ![]() over the range
over the range ![]() of sampling times t. Thus, the expected limits in Figure 2 would be
of sampling times t. Thus, the expected limits in Figure 2 would be ![]() and
and ![]() as shown.
as shown.
The apparent oscillatory structure of the orange plot (μ0 = 105) in Figure 2 requires an explanation since there is no intrinsic periodicity in the case of a constant decay rate λ. (We will come to the statistics of a periodic decay rate in Section 3.) From pdf (9) one infers that the center-to-center displacement of the PG distributions of two samples taken respectively at times tn and ![]() is
is![]() , whereas the full width (standard deviation) of either distribution is
, whereas the full width (standard deviation) of either distribution is![]() . Therefore the individual distributions in the sum in expression (9) are resolved when
. Therefore the individual distributions in the sum in expression (9) are resolved when ![]() or
or
![]() (13)
(13)
in terms of the lifetime![]() . Figure 3 shows the results of superposing 1 (red), 2 (green), 3 (blue), and 5 (black) time-sequential Poisson-Gauss distributions of initial activity μ0 = 105 of a radioactive source with lifetime T0 = (A) 50, (B) 125, and (C) 200. The increasing lifetimes lead to a progression of MPG distributions with (A) completely resolved, (B) partially resolved, and (C) unresolved individual PG maxima. Application of criterion (13) to Figure 3(A) yields
. Figure 3 shows the results of superposing 1 (red), 2 (green), 3 (blue), and 5 (black) time-sequential Poisson-Gauss distributions of initial activity μ0 = 105 of a radioactive source with lifetime T0 = (A) 50, (B) 125, and (C) 200. The increasing lifetimes lead to a progression of MPG distributions with (A) completely resolved, (B) partially resolved, and (C) unresolved individual PG maxima. Application of criterion (13) to Figure 3(A) yields ![]() (resolved maxima), whereas application to
(resolved maxima), whereas application to
Figure 3(C) yields ![]() (unresolved maxima).
(unresolved maxima).
We conclude this section by examining the statistical moments of a mixed Poisson-Gauss random variable with probability density (8), which can be obtained by summation of the moments of the independent PG variates. The kth moment ![]()
![]() of a PG variate observed at time t can be expressed in the form [27] .
of a PG variate observed at time t can be expressed in the form [27] .
![]() . (14)
. (14)
Summation of (14) over the range of t and expansion of ![]() in a binomial series leads to the kth moment of the MPG random variable
in a binomial series leads to the kth moment of the MPG random variable
![]() (15)
(15)
in which ![]() is the standard gamma function, and the last factor in Equation (15) arises from the sum of a geometric series
is the standard gamma function, and the last factor in Equation (15) arises from the sum of a geometric series![]() . It is seen from (15) that only even values of the index j contribute to the MPG moments.
. It is seen from (15) that only even values of the index j contribute to the MPG moments.
Expansion of Equation (15) leads to the series
![]() (16)
(16)
in which sequential terms decrease by powers of![]() . Consequently, under conditions of high initial activity,
. Consequently, under conditions of high initial activity, ![]() , the most significant contribution by orders of magnitude is just the first term. The first term, itself, can be further approximated, depending on the values of λ and λT compared with 1:
, the most significant contribution by orders of magnitude is just the first term. The first term, itself, can be further approximated, depending on the values of λ and λT compared with 1:
![]() (17)
(17)
From the moments Mk given by (15), one can calculate the variance ![]() (or standard deviation
(or standard deviation![]() ),
),
![]() , (18)
, (18)
the skewness Sk
![]() , (19)
, (19)
and kurtosis K
![]() , (20)
, (20)
which are the statistics most commonly used to characterize a probability distribution in atomic and nuclear physics. Skewness describes the asymmetry about the mean, and kurtosis is a measure of the concentration of probability around the shoulders (i.e. at about ±1σ from the mean) and tails. A distribution with high kurtosis would be sharply peaked with fat tails, i.e. with higher than normal probability of outliers (such as produced by a Cauchy distribution). Thus, the shapes of the pdfs plotted in Figure 2 appear to have a higher skewness and lower kurtosis than a normal or Poisson distribution whose statistics, for comparison, are
![]() (21)
(21)
Explicit expressions for relations (18)-(20) are complicated and will not be given here. It is to be noted, however, that from the form ![]() of (17), the initial activity
of (17), the initial activity ![]() divides out of the expressions for skewness and kurtosis, which therefore depend only on λ and T. Figure 4 shows plots of the standard deviation, skewness, and kurtosis as a function of duration T for fixed decay rate
divides out of the expressions for skewness and kurtosis, which therefore depend only on λ and T. Figure 4 shows plots of the standard deviation, skewness, and kurtosis as a function of duration T for fixed decay rate![]() . For total sampling time T short with respect to mean lifetime
. For total sampling time T short with respect to mean lifetime![]() , the three functions all increase approximately linearly with T; kurtosis remains below 3, the Gaussian standard of comparison. For large durations T such that
, the three functions all increase approximately linearly with T; kurtosis remains below 3, the Gaussian standard of comparison. For large durations T such that![]() , skewness and kurtosis again vary roughly linearly with T, although at different rates than previously; the standard deviation has
, skewness and kurtosis again vary roughly linearly with T, although at different rates than previously; the standard deviation has
![]()
Figure 4. Plot of (A) standard deviation (black), (B) skewness (red), and (C) kurtosis (blue) of a mixed Poisson-Gauss distribution as a function of total measurement time T for decay rate λ = 10−3.
reached a maximum at around ![]() and then decreased at an approximately linear rate. The decrease in
and then decreased at an approximately linear rate. The decrease in ![]() with T in the domain of high T is consistent with the narrowing of the peak of the probability density (9) plotted in Figure 1(A) and Figure 1(B) (e.g. plots e, f, g) as the pdf approaches the limiting expression (12).
with T in the domain of high T is consistent with the narrowing of the peak of the probability density (9) plotted in Figure 1(A) and Figure 1(B) (e.g. plots e, f, g) as the pdf approaches the limiting expression (12).
2.2. Radioactivity at Time-Varying Decay Rate ![]()
A characteristic of non-standard radioactive decay predicted or reported in publications cited in Section 1 is the harmonic variation of the decay rate. This feature leads to a time-dependent mean activity of the form
![]() (22)
(22)
in the simplest case of a single harmonic component. The statistical consequences of relation (22) are examined in detail in this section for various relative values of the lifetime T0, periodicity T1, and count duration T (which is equal to the number of PG samples in the time series), and for amplitude![]() . The latter condition on amplitude―in particular the stronger statement
. The latter condition on amplitude―in particular the stronger statement![]() ―must obviously pertain, since otherwise violations of the Rutherford-Soddy law would have been noticed unambiguously many years ago.
―must obviously pertain, since otherwise violations of the Rutherford-Soddy law would have been noticed unambiguously many years ago.
Figure 5 shows the variation in the MPG probability density
![]() , (23)
, (23)
with μt given by Equation (22), as a function of normalized activity ![]() for initial mean activity μ0 = 104, lifetime T0 = 100, duration T = 100 and period T1 = (A) 10, (B) 50, (C) 200. In each panel the color of the individual plots denotes the value of the amplitude:
for initial mean activity μ0 = 104, lifetime T0 = 100, duration T = 100 and period T1 = (A) 10, (B) 50, (C) 200. In each panel the color of the individual plots denotes the value of the amplitude: ![]() (red), 0.005 (blue), 0.010 (green), 0.015 (black). The red curves serve as standard radioactive decay baselines against which to compare the visibility of the harmonic deviations. One sees from the progression of panels that the presence of a harmonic component to the decay rate leads to oscillations in the probability density (23). The amplitude of the oscillations increases with increasing
(red), 0.005 (blue), 0.010 (green), 0.015 (black). The red curves serve as standard radioactive decay baselines against which to compare the visibility of the harmonic deviations. One sees from the progression of panels that the presence of a harmonic component to the decay rate leads to oscillations in the probability density (23). The amplitude of the oscillations increases with increasing ![]() and decreases with increasing T1.
and decreases with increasing T1.
The explanation of the second property is reasonably self-evident from the form of expression (22). In the limiting case of![]() , the maximum value of the argument of the cosine is
, the maximum value of the argument of the cosine is![]() , and therefore the mean activity would appear to vary in accord with the Rutherford-Soddy law,
, and therefore the mean activity would appear to vary in accord with the Rutherford-Soddy law, ![]() , but with a decay rate given by
, but with a decay rate given by![]() .
.
The manifestation of the first property may likewise seem unsurprising, but there is a subtlety to the question why oscillations occur in the first place. It is important to keep in mind that the function ![]() in Equation
in Equation
![]()
Figure 5. Variation of probability density ![]() as a function of normalized activity
as a function of normalized activity ![]() for initial mean activity μ0 = 104, lifetime T0 = 100, time series duration T = 100, and periodicity T1 = (A) 10, (B) 50, (C) 200 with amplitude α = 0 (red), 0.005 (blue), 0.010 (green), 0.015 (black).
for initial mean activity μ0 = 104, lifetime T0 = 100, time series duration T = 100, and periodicity T1 = (A) 10, (B) 50, (C) 200 with amplitude α = 0 (red), 0.005 (blue), 0.010 (green), 0.015 (black).
(23)―or the transformed equivalent![]() ―is a probability density function; i.e. it is the theoretical expression against which an empirical histogram of discrete nuclear disintegrations would be compared. Statistically, a histogram is a plot of frequency of occurrence against category in which all the events that make up a particular category (e.g. number of nuclear decays that fall within a certain range) may have been recorded at different times throughout the total period T of counting. In other words, reference to timing is ordinarily completely lost in a histogram. (This point was of major significance in one of the refutations to previous claims of observed non-standard nuclear decay [18] .) Why, then, do oscillations occur in the plots of Figure 4? Note that the horizontal axis is not a time axis, and the period of the oscillations is not T1.
―is a probability density function; i.e. it is the theoretical expression against which an empirical histogram of discrete nuclear disintegrations would be compared. Statistically, a histogram is a plot of frequency of occurrence against category in which all the events that make up a particular category (e.g. number of nuclear decays that fall within a certain range) may have been recorded at different times throughout the total period T of counting. In other words, reference to timing is ordinarily completely lost in a histogram. (This point was of major significance in one of the refutations to previous claims of observed non-standard nuclear decay [18] .) Why, then, do oscillations occur in the plots of Figure 4? Note that the horizontal axis is not a time axis, and the period of the oscillations is not T1.
The occurrence and number of periodic maxima and minima in a plot of pdf (23) as a function of activity can be accounted for by an explanation similar (but not identical) to the explanation of oscillatory structure in the orange plot of Figure 2. Because![]() , the Gaussian exponential in (23) acts like a Dirac delta function, vanishing rapidly for all values of x except in a very narrow time interval about those specific times t when
, the Gaussian exponential in (23) acts like a Dirac delta function, vanishing rapidly for all values of x except in a very narrow time interval about those specific times t when![]() , or equivalently when
, or equivalently when
![]() . (24)
. (24)
Thus a histogram governed by pdf (23) with ![]() actually does to a significant extent preserve temporal information regarding disintegration events. This point is demonstrated in Figure 6.
actually does to a significant extent preserve temporal information regarding disintegration events. This point is demonstrated in Figure 6.
Figure 6(A) shows two plots of the normalized mean activity ![]() as a function of time―i.e. the decay curve―for measurement conditions corresponding to Figure 5(A). The red transient in Figure 6(A) is the decay curve that would be produced by a time-varying radioactive decay rate with harmonic amplitude
as a function of time―i.e. the decay curve―for measurement conditions corresponding to Figure 5(A). The red transient in Figure 6(A) is the decay curve that would be produced by a time-varying radioactive decay rate with harmonic amplitude ![]() and period T1 = 10. The horizontal solid black lines mark the numerical values of the activities z corresponding to the nine peaks in Figure 5(A). It is seen that these lines intersect the red decay curve along segments that, at the scale of the figure, look nearly flat. Figure 6(B) shows four of the intersections more clearly over the expanded time range from 50 to 90 time units. The horizontal lines intersect each horizontal sinusoidal segment precisely at the midpoint, i.e. at the point of inflection where the curvature changes from positive to negative. In other words, the most significant contributions to the sum in pdf (23) come from narrow regions about stationary points of the decay transient.
and period T1 = 10. The horizontal solid black lines mark the numerical values of the activities z corresponding to the nine peaks in Figure 5(A). It is seen that these lines intersect the red decay curve along segments that, at the scale of the figure, look nearly flat. Figure 6(B) shows four of the intersections more clearly over the expanded time range from 50 to 90 time units. The horizontal lines intersect each horizontal sinusoidal segment precisely at the midpoint, i.e. at the point of inflection where the curvature changes from positive to negative. In other words, the most significant contributions to the sum in pdf (23) come from narrow regions about stationary points of the decay transient.
Another important feature to note is illustrated by the blue trace in Figure 6(A) (which has been displaced downward by 0.2 for visibility). This is the decay curve associated with the pdf of largest harmonic amplitude ![]() shown in Figure 5(A). Although the periodic structure of the pdf in Figure 5(A) is strikingly large, the oscillations at period T1 = 10 in the blue transient of Figure 6(A) are barely visible. This suggests that the distribution of decay events is a much more sensitive indicator of radioactive decay with time-dependent decay rate than is the decay transient (21).
shown in Figure 5(A). Although the periodic structure of the pdf in Figure 5(A) is strikingly large, the oscillations at period T1 = 10 in the blue transient of Figure 6(A) are barely visible. This suggests that the distribution of decay events is a much more sensitive indicator of radioactive decay with time-dependent decay rate than is the decay transient (21).
It is a well-known principle of time series analysis that one cannot measure the period T1 of a harmonic component if the duration T of the series is shorter than the period![]() . However, it is possible to detect the presence of such a component. For example, a partial-period component, if present in the decay rate of a radioactive nuclide, would be equivalent to a trend and therefore contribute to low-frequency oscillations in the power spectrum. Such a signal was searched for (but not found) as part of a recent comprehensive experimental investigation of the
. However, it is possible to detect the presence of such a component. For example, a partial-period component, if present in the decay rate of a radioactive nuclide, would be equivalent to a trend and therefore contribute to low-frequency oscillations in the power spectrum. Such a signal was searched for (but not found) as part of a recent comprehensive experimental investigation of the ![]() decay of 22Na [18] . The presence of a partial-period component is also manifested in the distribution of decay events, as shown in Figure 7 for initial mean activity μ0 = 106, lifetime T0 = 1000, measurement time T = 1000 and increasing periods T1 = (A) 1500, (B) 2000, (C) 4000. The plots are color-coded for amplitude:
decay of 22Na [18] . The presence of a partial-period component is also manifested in the distribution of decay events, as shown in Figure 7 for initial mean activity μ0 = 106, lifetime T0 = 1000, measurement time T = 1000 and increasing periods T1 = (A) 1500, (B) 2000, (C) 4000. The plots are color-coded for amplitude: ![]() (red), 0.05 (blue), 0.10 (green), 0.2 (black). One sees from the progression of
(red), 0.05 (blue), 0.10 (green), 0.2 (black). One sees from the progression of
![]()
Figure 7. Variation of probability density ![]() as a function of normalized activity
as a function of normalized activity ![]() for initial mean activity μ0 = 106, lifetime T0 = 1000, time series duration T = 1000, and periodicity T1 = (A) 1500, (B) 2000, (C) 4000 with amplitude α = 0 (red), 0.05 (blue), 0.10 (green), 0.2 (black).
for initial mean activity μ0 = 106, lifetime T0 = 1000, time series duration T = 1000, and periodicity T1 = (A) 1500, (B) 2000, (C) 4000 with amplitude α = 0 (red), 0.05 (blue), 0.10 (green), 0.2 (black).
panels that relatively high amplitudes ![]() are required to see structure above the red base curve, and that this structure diminishes as the ratio
are required to see structure above the red base curve, and that this structure diminishes as the ratio ![]() increases. As a practical matter, the period T1 need not be a significant experimental limitation, since it is often possible to increase the duration T of the time series.
increases. As a practical matter, the period T1 need not be a significant experimental limitation, since it is often possible to increase the duration T of the time series.
3. Statistics of Nuclear Lifetime Measurements
3.1. Distribution of Two-Point Lifetimes at Constant Decay Rate λ
A standard procedure for measuring the half-life ![]() (5)―or, equivalently, the lifetime T0 (inverse decay rate)― of a radionuclide is to record the decay curve as a function of time. For a single unstable state decaying exponentially, a log plot generates a straight line from whose slope the lifetime can be determined. An alternative procedure for determining nuclear lifetimes is based on the statistical distribution of two-point lifetime estimates obtained from a time series of measured activities
(5)―or, equivalently, the lifetime T0 (inverse decay rate)― of a radionuclide is to record the decay curve as a function of time. For a single unstable state decaying exponentially, a log plot generates a straight line from whose slope the lifetime can be determined. An alternative procedure for determining nuclear lifetimes is based on the statistical distribution of two-point lifetime estimates obtained from a time series of measured activities![]() ,
, ![]()
![]() in the following way [23] .
in the following way [23] .
For each pair of activities ![]() corresponding to measurement times
corresponding to measurement times![]() , where
, where ![]()
![]() ,
,
・ calculate the lifetime from the two-point relation
![]() ; (25)
; (25)
・ make a histogram of the ![]() estimates given by Equation (25);
estimates given by Equation (25);
・ locate the center of the resulting distribution.
Under the conditions that (1) the number of decays per sampling interval Δt is sufficiently high, (2) the number of sequential activity measurements is sufficiently large, and (3) the lifetime is sufficiently long compared to time intervals between pairs of samples, the probability density of two-point estimates is virtually indistinguishable from a Cauchy distribution centered on the true lifetime T0.
Given that the activities Ai are (to excellent approximation) Poisson-Gauss (PG) variates, and that the inverse of the logarithm of the ratio of PG variates involves complicated transformations of the Gaussian probability density, it is perhaps highly surprising that the distribution of the variates Tij turns out to be described by a simple, symmetric Cauchy function. Actually, the exact density function is far more complicated than a Cauchy function, but reduces to the latter under the previously enumerated conditions, as derived in [23] . The derivation will not be repeated here, but a more exact expression for the theoretical pdf will be given below, followed by a brief explanation of how it was obtained and how it differs from the pdf published in [23] .
Let θ be a continuous random variable whose realizations are the samples Tij in the population of Nt samples obtained from the sequential measurement of a time series of T activities. And let J be the “multiplicity” of a measurement, whose significance will be explained shortly. Then the probability density function of two-point lifetime estimates takes the form
![]() (26)
(26)
which will be denoted simply by ![]() when there is no ambiguity regarding parameters.
when there is no ambiguity regarding parameters.
The derivation of relation (26) involves three sequential transformations of the pdfs of functions of the variables ![]() and
and![]() .
.
Step 1:![]() .
.
Step 2:![]() .
.
Step 3:![]() .
.
in which the transformation at each step is implemented by a relation of the form of Equation (10)
![]() (27)
(27)
where![]() . Specific expressions for transforming functions of Poisson and Gaussian variates are given in [27] and [28] , and tested experimentally by means of branched nuclear decay processes in [28] .
. Specific expressions for transforming functions of Poisson and Gaussian variates are given in [27] and [28] , and tested experimentally by means of branched nuclear decay processes in [28] .
There are three principal differences between Equation (26) and the corresponding pdf published previously in [23] . First, the variate in (26) is “lifetime”, not “half-life”, whereupon various factors of ln2 are absent. Second and of greater significance, the pdf of the quotient of two random variables (Step 1 above) was derived more exactly in (26) than in the pdf in [23] . Approximations were made in [23] to show how an empirically discovered procedure for measuring nuclear half-lives resulted in a Cauchy distribution. The intent of the present paper is entirely different―namely, to examine the statistical basis of a measurement procedure by which to search for violations of a fundamental physical law, i.e. the law of radioactive decay. The two expressions for pdf ![]() lead to nearly identical numerical results in the case of radioactive decay at constant decay rate, but small discrepancies could occur for radioactive decay at time-varying decay rate.
lead to nearly identical numerical results in the case of radioactive decay at constant decay rate, but small discrepancies could occur for radioactive decay at time-varying decay rate.
The third difference is the inclusion of the multiplicity J in (26), which is absent from the analysis in [23] . Multiplicity refers to the number of activity measurements taken within a counting interval Δt and averaged to
give the mean activity ![]() at time t. If the activity xt is a PG variate of variance
at time t. If the activity xt is a PG variate of variance![]() , then
, then ![]() is a
is a
PG variate ![]() of variance
of variance![]() . Although the random variable θ for the two-point lifetime is not even approximately a PG variate, multiple sampling and averaging can nevertheless have a dramatic effect on reducing the width and altering the shape of the density function (26), as illustrated in Figure 8.
. Although the random variable θ for the two-point lifetime is not even approximately a PG variate, multiple sampling and averaging can nevertheless have a dramatic effect on reducing the width and altering the shape of the density function (26), as illustrated in Figure 8.
The red plots in Figure 8 show the variation of the theoretical pdf ![]() (solid lines) for standard radioactive decay (
(solid lines) for standard radioactive decay (![]() ) with initial mean activity μ0 = 106, lifetime T0 = 500, number of time bins T = 250, and sampling multiplicity J = (A) 1 and (B) 25. From the relation following Equation (25) the total number of two-point estimates Tij is Nt = 31,125. The solid red traces in Figure 8(A) and Figure 8(B) strongly resemble Cauchy functions (and pass chi-square tests of goodness of fit). The trace in Figure 8(B), however, is narrower by a factor of about 5 (determined from the width at half-maximum). Superposed on the theoretical traces are computer-simulated histograms (red points) obtained by (1) generating 250 PG variates
) with initial mean activity μ0 = 106, lifetime T0 = 500, number of time bins T = 250, and sampling multiplicity J = (A) 1 and (B) 25. From the relation following Equation (25) the total number of two-point estimates Tij is Nt = 31,125. The solid red traces in Figure 8(A) and Figure 8(B) strongly resemble Cauchy functions (and pass chi-square tests of goodness of fit). The trace in Figure 8(B), however, is narrower by a factor of about 5 (determined from the width at half-maximum). Superposed on the theoretical traces are computer-simulated histograms (red points) obtained by (1) generating 250 PG variates ![]() for Figure 8(A) and (2) averaging 25 variates
for Figure 8(A) and (2) averaging 25 variates ![]() at each t over the preceding range for Figure 8(B), and then applying relation (25). As seen in the figure, the predicted and simulated distributions agree very closely in both panels, but the scatter of points about the theoretical curve is much less in Figure 8(B). The black plots will be discussed in the next section.
at each t over the preceding range for Figure 8(B), and then applying relation (25). As seen in the figure, the predicted and simulated distributions agree very closely in both panels, but the scatter of points about the theoretical curve is much less in Figure 8(B). The black plots will be discussed in the next section.
An important point worth noting because of its experimental consequences is that a Cauchy distribution, in contrast to Poisson and Gaussian distributions, has no finite moments (apart from the 0th moment, which equals 1 as required by the completeness relation for probability). The moment-generating function does not exist, and although the characteristic function (Fourier transform of probability density) does exist, it does not lead to finite moments [29] . One could, of course, calculate a sample mean and variance for any finite sample of data governed by a Cauchy distribution, but repeated sampling would not result in reduced variance and more sharply determined mean. It may be surprising to many physicists, but the mean of 100 measurements of a Cauchy-dis- tributed variate is no more precise than 1 measurement [27] . The reason for this striking violation of the Central Limit Theorem [30] is due to the so-called fat tails of the Cauchy distribution. Whereas a Gaussian function falls off exponentially with distance from the mean, the tails of a Cauchy function ![]() fall off more slowly as a power law
fall off more slowly as a power law![]() . Thus, the higher probability of obtaining an outlier upon repeated sampling effectively negates the benefit accruing from multiple samples. A Cauchy distribution, however, does have a finite median (and variance of the median). The median, in fact, is the statistic corresponding to the center of the histogram of two-point lifetime measurements.
. Thus, the higher probability of obtaining an outlier upon repeated sampling effectively negates the benefit accruing from multiple samples. A Cauchy distribution, however, does have a finite median (and variance of the median). The median, in fact, is the statistic corresponding to the center of the histogram of two-point lifetime measurements.
In view of the preceding remarks, the question may arise as to why, if relation (26) reduces for all practical purposes to a Cauchy distribution in the case of standard radioactive decay, does a multiplicity ![]() sharpen the distribution, as is evident in Figure 8(B). The answer is this: the narrower distribution shown in Figure 8(B) did not arise because the statistics of the population
sharpen the distribution, as is evident in Figure 8(B). The answer is this: the narrower distribution shown in Figure 8(B) did not arise because the statistics of the population ![]() distributed in Figure 8(A) are now better known, but because multiple sampling increased the precision of knowledge of the activities
distributed in Figure 8(A) are now better known, but because multiple sampling increased the precision of knowledge of the activities![]() , thereby creating a new and different population of two-point lifetime measurements
, thereby creating a new and different population of two-point lifetime measurements![]() .
.
3.2. Distribution of Lifetime Measurements at Variable Decay Rate ![]()
The derivation of pdf (26) does not depend on the form of the decay rate, but is valid for any non-pathological functional form for the mean activity![]() , including relation (22). Figure 8 and Figure 9 illustrate comparatively the shape of the plots (solid black) of pdf (26) for a suite of increasing values of amplitude
, including relation (22). Figure 8 and Figure 9 illustrate comparatively the shape of the plots (solid black) of pdf (26) for a suite of increasing values of amplitude ![]() for the experimental parameters cited previously for the red plots of Figure 8.
for the experimental parameters cited previously for the red plots of Figure 8.
Figure 8(A) and Figure 8(B) illustrate the advantage of multiple sampling and averaging for discerning the difference between standard nuclear decay (solid red) ![]() and non-standard nuclear decay (solid black) with harmonic amplitude
and non-standard nuclear decay (solid black) with harmonic amplitude ![]() and period T1 = 100. Whereas the two plots are virtually indistinguishable in Figure 8(A)
and period T1 = 100. Whereas the two plots are virtually indistinguishable in Figure 8(A)![]() , they are observably different in Figure 8(B)
, they are observably different in Figure 8(B)![]() . Superposed over each theoretical plot are points comprising the corresponding computer-simulated histograms constructed in the manner described in the previous section. Agreement between the black histogram and black theoretical curve bear out the statement above that the validity of pdf (26) is not limited to nuclear decay at constant decay rate. A minor point to note is that the plots in Figure 8 (and also in Figure 9) are of probability, rather than probability density. The former differs from the latter only by a constant factor equal to the histogram bin width Δ = 0.125. In plots of histograms the ordinate is usually probability, but this distinction is immaterial since only relative shape, and not scale, is of importance here.
. Superposed over each theoretical plot are points comprising the corresponding computer-simulated histograms constructed in the manner described in the previous section. Agreement between the black histogram and black theoretical curve bear out the statement above that the validity of pdf (26) is not limited to nuclear decay at constant decay rate. A minor point to note is that the plots in Figure 8 (and also in Figure 9) are of probability, rather than probability density. The former differs from the latter only by a constant factor equal to the histogram bin width Δ = 0.125. In plots of histograms the ordinate is usually probability, but this distinction is immaterial since only relative shape, and not scale, is of importance here.
Figure 9 shows the evolution of the distribution of two-point lifetimes (black) with increasing ![]() for fixed multiplicity J = 25 (other parameters also remaining fixed) in comparison with the distribution for standard radioactivity with
for fixed multiplicity J = 25 (other parameters also remaining fixed) in comparison with the distribution for standard radioactivity with ![]() (red). To enhance clarity of the figures, the points of computer-simulated histograms
(red). To enhance clarity of the figures, the points of computer-simulated histograms
![]()
Figure 9. Variation of two-point lifetime probability (solid black) with harmonic amplitude α = (A) 0.003, (B) 0.005, (C) 0.010 for the same parameters as in Figure 8(B). Superposed is the corresponding pdf (solid red) for standard radioactive decay (α = 0).
were omitted although, as in Figure 8, the histograms were generated and agreed closely with theoretical predictions. With increasing values of![]() , the black curves become increasingly bimodal and distinguishable from a Cauchy distribution. The sensitivity of this statistical method for probing non-standard radioactive decay is seen to be of order 10−3 in the figure, but higher sensitivities are achievable.
, the black curves become increasingly bimodal and distinguishable from a Cauchy distribution. The sensitivity of this statistical method for probing non-standard radioactive decay is seen to be of order 10−3 in the figure, but higher sensitivities are achievable.
Figure 10 shows the content of pdf (26) from a different perspective: the variation in shape as a function of multiplicity J for fixed amplitude ![]() (A) 10−3, (B) 5 × 10−4, (C) 0. In each panel, the plots are color-coded for increasing values of J from a minimum of 1 to maximum of 225. Comparison of plots of the same color shows that with increasing J, the differences between distributions for non-standard and standard radioactive decay becomes readily discernible even at values of the harmonic amplitude
(A) 10−3, (B) 5 × 10−4, (C) 0. In each panel, the plots are color-coded for increasing values of J from a minimum of 1 to maximum of 225. Comparison of plots of the same color shows that with increasing J, the differences between distributions for non-standard and standard radioactive decay becomes readily discernible even at values of the harmonic amplitude ![]() of order 10−4.
of order 10−4.
4. Power Spectrum and Autocorrelation Function
Deviations from standard nuclear decay due to a periodic decay rate of amplitude ![]() are scarcely discernible, if at all, in the decay curve, as demonstrated in Figure 6. We examine in this section the sensitivity of two commonly employed tools for probing the spectral content of a time series of data: power spectral analysis and autocorrelation.
are scarcely discernible, if at all, in the decay curve, as demonstrated in Figure 6. We examine in this section the sensitivity of two commonly employed tools for probing the spectral content of a time series of data: power spectral analysis and autocorrelation.
![]()
Figure 10. Variation of two-point lifetime pdf (26) for parameters μ0 = 106, T0 = 500, T1 = 50, T = 250, and amplitude α = (A) 0.001, (B) 0.0005, (C) 0. In each panel the color code of the multiplicity is J = 1 (red), 25 (blue), 100 (green), 225 (black).
A discrete time series ![]() can be represented by a Fourier series
can be represented by a Fourier series
![]() (28)
(28)
with ![]() independent power spectral amplitudes (apart from a0) in accordance with the Shannon sampling theorem [31]
independent power spectral amplitudes (apart from a0) in accordance with the Shannon sampling theorem [31]
![]() . (29)
. (29)
To any time series of finite length T sampled at intervals Δt there is a fundamental frequency
![]() (30)
(30)
and a cut-off frequency
![]() . (31)
. (31)
If the series contains a periodic component at frequency![]() , then the period and harmonic number are related by
, then the period and harmonic number are related by
![]() . (32)
. (32)
The discrete autocorrelation function rk of lag k (in units of Δt) is defined by
![]() (33)
(33)
with series mean
![]() . (34)
. (34)
It is usual procedure to detrend a series, i.e. transform to a series of zero mean and zero trend, before performing the operation (33). This also leads to ![]() in (28). The maximum lag number
in (28). The maximum lag number ![]() is somewhat arbitrary, but there are statistical reasons for setting
is somewhat arbitrary, but there are statistical reasons for setting ![]() to be less than about
to be less than about ![]() [32] .
[32] .
The left suite of panels in Figure 11 shows the variation in power spectrum (black) of a time series of nonstandard radioactive decay with parameters μ0 = 106, T0 = 500, T1 = 50, T = 1000, as a function of increasing amplitude ![]() (A) 0.01, (B) 0.10, (C) 0.30. The red plots, displaced downward for visibility, show the
(A) 0.01, (B) 0.10, (C) 0.30. The red plots, displaced downward for visibility, show the ![]()
![]()
Figure 11. Double-log plot of power spectral amplitudes Sj (A)-(C) (black) as a function of harmonic number j and corresponding autocorrelation coefficients rk (D)-(F) (black) as a function of lag interval k for parameters μ0 = 106, T0 = 500, T1 = 50, T = 1000, and α = (A), (D) 0.01, (B), (E) 0.10, (C), (F) 0.30. Plots in red, displaced downward for visibility in panels (A)-(E), are α = 0 (standard radioactive decay). Arrows show incipient spectral lines at lnj ≈ (A) 3.0 and (C) 3.7, corresponding respectively to fundamental T1 and first harmonic T1/2. Best-fit lines to the power spectra have a slope very close to −2, corresponding to Brownian noise.
spectrum (standard radioactive decay) for comparison. The theoretical power spectrum of the decay curve generated from the time-dependent activity (22) contains spectral lines corresponding to periods ![]() for integers
for integers ![]() As shown in Figure 11(A), the harmonic contribution to the decay rate is virtually undetectable in the power spectrum for
As shown in Figure 11(A), the harmonic contribution to the decay rate is virtually undetectable in the power spectrum for ![]() less than about 0.01, and the first harmonic (Figure 11(C)) becomes detectable only at
less than about 0.01, and the first harmonic (Figure 11(C)) becomes detectable only at![]() .
.
Since the autocorrelation is calculable from the power spectrum by means of the Wiener-Khinchine relations [33] (the power spectrum and autocorrelation constitute a Fourier transform pair), one might expect autocorrelation to yield results of comparable sensitivity. That this is effectively the case is shown by the right suite of panels in Figure 11 in which are plotted (black) the autocorrelation functions for the same set of fixed parameters and amplitudes ![]() (D) 0.01, (E) 0.10, (F) 0.30. As before, the plots in red refer to standard nuclear decay,
(D) 0.01, (E) 0.10, (F) 0.30. As before, the plots in red refer to standard nuclear decay,![]() . Theoretically, the autocorrelation as a function of lag time k of the time series of activities
. Theoretically, the autocorrelation as a function of lag time k of the time series of activities ![]() governed by pdf (23) should display a sinusoidal oscillation at fundamental period T1. The barest indication of oscillatory structure is seen in Figure 11(E) at an amplitude
governed by pdf (23) should display a sinusoidal oscillation at fundamental period T1. The barest indication of oscillatory structure is seen in Figure 11(E) at an amplitude![]() . By about
. By about ![]() the oscillations are sufficiently developed that it is no longer necessary to displace the
the oscillations are sufficiently developed that it is no longer necessary to displace the ![]() curve downward for visibility.
curve downward for visibility.
To summarize, analysis indicates that a periodic contribution to the radioactive decay rate would be detectable in the power spectrum and autocorrelation of the decay curve for harmonic amplitudes ![]() of a few parts in 100. It is to be noted that in a previous use of power spectral analysis to search for a periodic component to the
of a few parts in 100. It is to be noted that in a previous use of power spectral analysis to search for a periodic component to the ![]() decay rate of 22Na a sensitivity of one part in 1000 was demonstrated [18] . There is no inconsistency here. 22Na has a half-life of approximately 2.6 y, or lifetime
decay rate of 22Na a sensitivity of one part in 1000 was demonstrated [18] . There is no inconsistency here. 22Na has a half-life of approximately 2.6 y, or lifetime ![]() y. The total counting time T of the reported experiment was 167 h, which constituted only about 0.5% of the lifetime. Thus, the ~106 measurements were to a large extent samples from the same population of Poisson variates. The decay factor
y. The total counting time T of the reported experiment was 167 h, which constituted only about 0.5% of the lifetime. Thus, the ~106 measurements were to a large extent samples from the same population of Poisson variates. The decay factor ![]() differed measurably but insignificantly from unity, and the experiment did not probe a mixed Poisson-Gauss distribution. The sensitivity reported in [18] applied to power spectral analysis of a time-varying mean of the form
differed measurably but insignificantly from unity, and the experiment did not probe a mixed Poisson-Gauss distribution. The sensitivity reported in [18] applied to power spectral analysis of a time-varying mean of the form![]() , not that of relation (22).
, not that of relation (22).
5. Conclusions
Violations of the standard radioactive decay law, such as cited in Section 1, are weak at best and controversial. It is this author’s opinion that, at the present stage of investigation, alleged correlations, if indeed they exist, between the disintegration of radioactive nuclei and external events of a geophysical, astrophysical, or cosmological nature are more likely to be attributable to unanticipated instrumental effects resulting from known physical interactions than to violations of current physical laws or to the manifestation of some new physical interaction. Nevertheless, physicists have been surprised before by unexpected violations of principles thought to have been previously well-established. The violation of parity conservation [34] first demonstrated in the beta decay of 60Co [35] is one such memorable example.
Because non-random nuclear decay, or nuclear decay influenced by environmental conditions external to the nucleus (apart from known processes such as electron capture), has far-reaching fundamental implications, it is important to search for such phenomena by sensitive methods that have the potential to yield reliable, unambiguous results. In this paper two such methods were investigated and found to be capable of yielding a higher sensitivity than any method yet tried: 1) the statistical distribution of nuclear activities and 2) the statistical distribution of two-point estimates of nuclear lifetime (or half-life).
Theoretical analyses and numerical simulations of non-standard radioactive decay processes undertaken for this paper and an earlier brief report [21] indicate that the preceding two statistical methods have the capacity to reveal a harmonic component to the nuclear decay rate with amplitude ![]() of the order of a few parts in 104, which exceeds the corresponding sensitivities of the decay curve, power spectrum, or autocorrelation function by at least two orders of magnitude. Implementation of these statistical methods requires 1) a radioactive source of initial high activity and 2) measurement of a sufficiently long time series of decay events so that the activities comprise a population of mixed Poisson-Gauss variates. Both conditions are readily achievable in nuclear metrology labs for some of the nuclides (listed in Section 1) claimed to violate the standard radioactive decay law.
of the order of a few parts in 104, which exceeds the corresponding sensitivities of the decay curve, power spectrum, or autocorrelation function by at least two orders of magnitude. Implementation of these statistical methods requires 1) a radioactive source of initial high activity and 2) measurement of a sufficiently long time series of decay events so that the activities comprise a population of mixed Poisson-Gauss variates. Both conditions are readily achievable in nuclear metrology labs for some of the nuclides (listed in Section 1) claimed to violate the standard radioactive decay law.
The statistical methods reported here are most sensitive and quantitatively revealing when the harmonic contribution to the decay rate has a period T1 shorter than the duration T of the time series of measured activities. However, this ought not to be a serious constraint in effecting a search for violations of the radioactive decay law since 1) the periods T1 of primary interest are already known (i.e. they are the periods claimed to have been observed in published papers), and 2) the length of the time series is an experimentally adjustable parameter, which can be made larger by taking more data.