A Robust Estimation Method for Camera Calibration with Known Rotation ()
1. Introduction
If you visited a rock concert recently, or any other event that attracts crowds, you probably recognized how many people are taking videos of the scenario, using their mobile phone cameras. Combining these video streams potentially allows viewing the scene from arbitrary angles or creating a new video with an artificially designed camera trajectory. This is one of the challenges of SceneNet1, which aims to develop software for aggregating such audio-visual recordings of public events, in order to create multi-view high quality video sequences. The general setup of the SceneNet computational infrastructure is depicted in Figure 1.
In order to achieve this goal, there are several challenges that require an efficient solution. The first challenge is the mobile infrastructure: the individual user needs to be related to the event, including time and location tags. Then, large amounts of audio-visual data need to be transferred via the cellular network to a server. To this end, we have developed a framework which reduces the transmitted data. In this framework the server performs spatial registration based on image features and sensor measurements that are computed on the devices. From this registration and from video quality measurements (also done on the devices), the server chooses a small subset of videos that are transferred to the server for the multi-view video generation. The bandwidth reduction is therefore a function of the minimal number of features and auxiliary data that is needed for an accurate spatial registration.
The second challenge is spatial registration, i.e. the task of determining the relative position and orientation of two video streams. This is the classical task of epipolar geometry which describes the relative geometry of two images depicting the same scene. It is encoded in a 3 × 3 singular matrix known as the fundamental matrix [1] . Estimating the fundamental matrix and thus the epipolar geometry, is a core ingredient for many of computer vision algorithms such as structure-from-motion [2] , vision-based robot navigation [3] and even for intra-operative guidance [4] .
A common practice, for estimating the fundamental matrix, is to use matching invariant features, e.g. SIFT, SURF, etc. followed by a robust model-fitting algorithm. Typically, a RANSAC [5] like algorithm that samples a set of putative correspondences until an outliers-free set is found. Outliers are defined as correspondences that do not agree with the estimated model yielded from the correspondences set. The main weakness of RANSAC- like scheme is the requirement of sampling a valid set, where all are inliers, with a high probability. The number of sampling subsets that are needed, to get a valid set, is exponential with the subset’s cardinality.
These days, it is common to use mobile cameras that have built-in sensors such as accelerometer, compass and gyros. These can be used for measuring the motion and orientation of the mobile camera. In this paper we present an algorithm for estimating the epipolar geometry given, the relative orientation of the cameras and the
![]()
Figure 1. The presented research is part of project SceneNet, which aim is to aggregate numerous audio-visual recordings of public events, captured by mobile devices (far left), in order to create a multi-view high quality video sequence. The data is transmitted via the cellular network to a high performance computing server, where it been synchronized, followed by the proposed spatial registration algorithm (middle bulb). The data will then be available through a dedicated viewer in which a user will be able to define an artificial camera that moves along a specific trajectory. To this end, in this paper, we present an image synthesis algorithm that can generate a convincing synthesized image from a specific camera pose. In addition, The event will create a community, where each member may provide another piece of the puzzle and view the entire information.
intrinsic parameters of the cameras. This allows computing an improved, accurate registration with less feature points than traditional algorithms [1] .
Given the spatially calibrated cameras, the ability to interactively control the viewpoint while watching a video, is an exciting application. This poses an additional challenge, i.e. an efficient image interpolation algorithm is required in order to obtain free viewpoint video.
Novel view interpolation, also known in the literature as image-based rendering (IBR), is a classic problem in computer vision and graphics [6] : given a collection of input video frames, synthesize images which would have been seen from viewpoints along a desired camera path. We propose a geometry-based approach that uses, except from the available images, the 3D structure, which has been generated in the spatial calibration stage.
The main challenge of novel view interpolation is how to robustly estimate pixel correspondences between two given cameras frames and to interpolate the pixel motion into the novel image in a coherent way. In the proposed approach each rendered image is constructed from two existing images of the two most similar cameras, by transferring triangular patches one at a time. The triangles were defined by the correspondences of the two existing images projected onto the novel view according to 3D structure that has been estimated. We do not impose strong assumption on the scene structure or the camera movement, allowing for arbitrary input and even for wide baseline setups.
The rest of the paper is organized as follows: Section 2 analyzes the complexity of the problem; Section 1 reviews the state of the art works that are related to this presentation; and Section 4.3 presents the spatial registration algorithm. In Section 5 we present the virtual image generating algorithm; Section 6 presents experimental results that validate the presented algorithms; and Section 7 concludes the presentation.
2. Complexity Analysis
In this section we give a theoretical and practical analysis of the computational complexity of the spatial registration algorithm for the specific problem of numerous users capturing the same scene.
The amount of data that needs to be transfer via the network is illustrated in the following example. Consider a Samsung Galaxy S6 device that records UHD video (3840 × 2160) with a bit-rate of 48 Mbps, and Full-HD video (1920 × 1080) with a bit-rate of 17 Mbps. In a moderate scene with 50 devices filming UHD and 50 devices filming Full-HD, the total bit-rate is accumulated to 3.25 Gbps. Hence, real-time transfer of all the videos to a common server is not feasible due to bandwidth limits of the wireless network which cannot exceed 500 Mbs for an individual user. The practical approach would be to submit only the detected features that can be computed on the device for each frame. This approach can be rendered insufficient since a typical number of detected features may be beyond several thousands. For example let n = 5000 be the number of features, and assume that each detected feature is described by a SIFT descriptor [7] of length d = 128 where each element is represented by an unsigned integer with 8-bits. Then, for each frame the mobile generates a total of n × d × 8 ≈ 5 Mb which may aggregates to 120 Mb/sec for 25 frames in a second. Hence, even with feature representation it won’t be possible to submit the data of more than 3 users to the server. One approach to solve this problem is to send only a subset of features. This requires a robust and accurate algorithm to solve the registration problem with a small subset of features. Such an algorithm is presented in this paper.
The core of the registration algorithm relies on comparisons between images. However, only images taken from nearby positions will give valuable results. Since, in the first frame we have no initial guess on the location of the cameras, we need to compare all the images pairs, which results in complexity of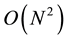 , for N cameras. For the following frames, however, we can reduce the complexity to
, for N cameras. For the following frames, however, we can reduce the complexity to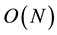 , by assuming a minor movements of the cameras, thus comparing each camera only with its neighbors. For T time-frames in a video, we get a total complexity of
, by assuming a minor movements of the cameras, thus comparing each camera only with its neighbors. For T time-frames in a video, we get a total complexity of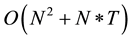 , and since for normal framerate
, and since for normal framerate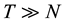 , the complexity become
, the complexity become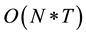 , and linear in the number of frames
, and linear in the number of frames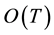 . Since the complexity cannot be reduced bellow linear, the only way to reduce the running time is to reduce the inner comparison computation time.
. Since the complexity cannot be reduced bellow linear, the only way to reduce the running time is to reduce the inner comparison computation time.
As an example consider the N = 50 cameras scenario described above. In order to initialize the spatial registration an order of 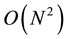 pairwise computations are required. As is described in Section 3, Each computation consists of a robust optimization procedure in order to estimate the fundamental matrix, which demand a set of 35 iterations for the propose algorithm where as 1177 are needed for the 8-point algorithm [8] a factor of 33 in favor of the proposed algorithm2. However, since the order of the number of pairwise comparisons is quadratic, the actual improvement factor is 332 ≈ 103. Hence, the registration algorithm described here requires the transmission of a smaller number of features, which results in a lower bandwidth consumption with an additional advantage of efficient computation time.
pairwise computations are required. As is described in Section 3, Each computation consists of a robust optimization procedure in order to estimate the fundamental matrix, which demand a set of 35 iterations for the propose algorithm where as 1177 are needed for the 8-point algorithm [8] a factor of 33 in favor of the proposed algorithm2. However, since the order of the number of pairwise comparisons is quadratic, the actual improvement factor is 332 ≈ 103. Hence, the registration algorithm described here requires the transmission of a smaller number of features, which results in a lower bandwidth consumption with an additional advantage of efficient computation time.
3. Related Work
The focus of the paper is on the spatial registration task and on synthesis of virtual camera images. Hence the description of the state-of-the-art on these topics is given in the following subsections.
3.1. Spatial Registration
In this section we review the relative pose estimating algorithm that are relevant to this correspondence. In order to determine the relative pose between two cameras, one need to estimate the fundamental or essential matrix. These matrices represent the epipolar geometry that described the relative geometry of two cameras.
The fundamental matrix, F, encapsulates the two cameras’ intrinsic parameters which are the focal lengths and the principle points, and the extrinsic parameters which include the relative orientation, and the translation vector from the first to the second camera. The intrinsic parameters are usually publicity available through the camera manufacturer or the operation system of the mobile device. Given the intrinsic parameters the problem reduced to estimating the essential matrix, E, that encode only the relative pose parameters.
Numerous methods have been proposed for estimating the fundamental matrix, which can be classified as linear, iterative and robust methods. There are a set of “n-point” feature-based algorithms to compute the fundamental matrix, or the essential matrix in case of known intrinsic parameters. The fundamental matrix can be estimated by the normalized-8-point algorithm [8] or 7-point algorithm [10] . If the camera is calibrated, or the intrinsic parameters are known a priori, an equivalent 6-point [11] and 5-point [9] algorithms have been deve- loped.
The performance of the “n-point” algorithm is significantly depends on the quality of the feature correspondences detected between the images. There are two main sources for degradation in the correspondences quality, (a) bad point localization due to image noise and (b) outliers caused by wrong matching between corresponding feature points. The “n-point” algorithms can compensate for feature localization errors by adding redundant points and solving a least-squares minimization problem. Alternatively, iterative methods are in general more accurate than the linear “n-point” methods. They use sophisticated computational approaches to solve a non- linear optimization problem [12] . One form of such non-linear optimization problem is to minimize a cost function that sums the distance between feature points and their corresponding epipolar lines [13] . Iterative methods are more accurate than the linear methods but are much more computationally expensive and cannot cope with outliers. Therefore they are impractical for real time application. Nevertheless, iterative methods are extensively used as refine procedure after getting an outlier free and accurate enough solution using robust and linear methods [14] .
Robust methods aim to tolerate both image noise and outliers. Robust parameters estimation in presence of outliers is a general problem in computer vision and thorough reviews can be found in [15] [16] . M-estimators [1] reduce the affect of outliers by using a heavy-tailed weighting function on the individual residuals. There are many M-estimators, each with its specific weight function. Another set of techniques is based on randomly selecting a subset of correspondences for computing an approximation of the fundamental matrix by a linear method. There are two major random sampling approaches: Least median of squares (LMedS) [17] and random sampling consensus (RANSAC) [5] . The difference between the two approach is in the way they determine the fundamental matrix. The chosen fundamental matrix, according to LMedS, is the one that minimize the median distance between the points and the corresponding epipolar lines. RANSAC compute the number of inliers for each computed matrix and choose the matrix with the maximum inliers.
The weak point of the sampling-based algorithms is the necessity to sample an oulier free set. The number of random samples needed to get an outlier free set depends exponentially on the number of elements required for the estimation and on the inlier fraction. Thus, reducing the size of the sampling set is of utmost importance when applying RANSAC scheme. For example, to get an outlier free sample with 99% certainty from a data set with 50% outlier ratio, one needs to sample 146 times while using the 5-point algorithm, 1177 times while using the 8-point algorithm, and 35 while using the proposed 3-point algorithm. A factor of 4 and 33 speedup, respectively. Hence, the proposed 3-point algorithm will be much more efficient, which might be very important for limited computational power devices such as smartphones.
In addition, RANSAC scheme can yield inaccurate hypothesis estimation due to image noise. In order to improve the performance of the RANSAC scheme many algorithms have been developed, such as LO-RANSAC [18] , PROSAC [19] , BEEM [20] , BLOGS [21] , and recently USAC [22] .
Recently, many researchers aim at exploiting auxiliary information either visual, like vanishing points, or using external sensor attached to the camera like Inertial Measurement Unit (IMU). For example, in [23] , camera motion is computed using both a monocular camera and an IMU in a complementary way. The problem of estimating the relative pose given two rotation angles has been investigate in [24] . In their algorithm the two rotation angles are given from the accelerometer sensor. Other approaches, e.g. [25] , used sensors’ measurement as auxiliary information and concentrate on the integration between vision-based and sensors-based pose estimation and their review is out of the scope of this paper. Closely related to the presented approach, Dalalyan and Keriven [26] formulate the relative pose estimation problem with known relative orientation as an inverse problem. Their optimization framework is a global one where all the parameters, the camera positions and outlier identities, are estimated simultaneously.
3.2. Virtual Camera
The developed approach was inspired by several state-of-the-art works on image-based rendering and image stabilization. A well established technique for image morphing is based on feature matching. For a survey of such methods see [27] . A modern approach is presented by Gurdan et al. [28] . Their multiview image interpolation algorithm is focused on synthesizing novel in-between images, and is based on sparse feature matching without any knowledge on calibration parameters. The main effort is, therefore, to robustly estimate pixel correspondences and subsequently interpolate the pixel motion properly. They presents convincing results of interpolated in-between image.
Other class of approaches for novel image synthesis is based on 3D structure information, usually reconstructed using standard structure-from-motion (SFM) algorithm [1] . Liu and Jin [29] proposed a video stabilization algorithm guided by structure from motion reconstruction. The 3D approach to video stabilization is closely related to our goals. In this context the camera path is estimated using SFM algorithm and a smooth path is fit to the noisy motion of the hand-held camera path. This setup reduces the problem into the image-based rendering (IBR) problem of novel view interpolation.
Recently, Kopf et al. [30] published an algorithm for creating hyper-lapse video, where a regular video is summarized by taking only the k-th frame. But, instead of taking just the k-th frame which can yield non-stabilized movie they estimate a smooth path using SFM algorithm and synthesis these images along the estimated path. Their approach, however, is limited to a single camera and may fail for large wide baseline camera setups.
4. Relative Pose Estimation for the Case of Known Rotation Matrix
Nowadays, cameras are often attached with high-quality sensors, such as accelerometer, magnetometer (compass) and gyro. In addition, for vision-based robot navigation, low-cost inertial measurement units (IMUs) based on micro-electro-mechanical systems (MEMS) devices can be used to estimate the relative pose.
In this section we present an effective algorithm that exploits sensors’ measurements for estimating the essential matrix and thus solves the relative pose problem. A short version of the proposed method has been presented at GAMM 2015, see [31] . In the following we outline the approach starting with the required mathematical background.
4.1. Mathematical Foundation
In this presentation we follow the standard notations and mathematical foundation presented in Hartley and Zisserman [1] .
The pinhole camera model is given by a projection matrix
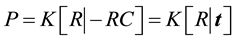 (1)
(1)
where K is the calibration matrix, R is the rotation matrix that rotates a vector in the world coordinate system to the camera’s reference frame, and C is the camera’s center of projection in the world coordinate system.
The calibration matrix is a 3 × 3 matrix that includes the focal length, and the principle point of projection. Practically, the image’s center point is commonly regarded as the principle point. The focal length can be estimated using dedicated algorithms, e.g., [32] , or by using camera’s manufacturers data, which can be extracted from EXIF metadata or through the mobile operation system.
4.2. Epipolar Geometr
The geometry that described the relative pose of two cameras is known as epipolar geometry [1] , and it is encapsulated in two 3 × 3 matrices: the fundamental matrix, F; and the essential matrix E.
The fundamental matrix is composed of the extrinsic parameters that describe the relative pose between the two views, and the intrinsic parameters that include the focal length and the principal point (center of projection) of the cameras. As stated above, the intrinsic parameters may be regarded as known, and can be extracted from the camera API and thus reduce the fundamental matrix to the essential matrix:
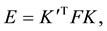 (2)
(2)
where any tagged symbol represents entities of the 2nd camera. The essential matrix E is composed of the relative rotation and translation,
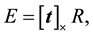 (3)
(3)
where 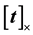 represents the cross-product matrix form:
represents the cross-product matrix form:
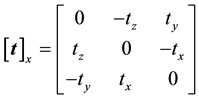 (4)
(4)
It has 5 degrees of freedom (DOF), 3 for the 3 rotation angles, and 2 for the normalized 3-vector that represents the translation between the two view.
In order to estimate the essential matrix and thus solve the relative pose problem, one uses the epipolar constraint equation:
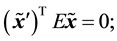 (5)
(5)
where 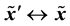 are normalized image points from the two view, i.e.,
are normalized image points from the two view, i.e., 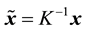 and
and![]() , that are projections of the same world point
, that are projections of the same world point![]() , i.e,
, i.e, ![]() and
and![]() . Note that image points are represented
. Note that image points are represented
by homogeneous vectors![]() . Different estimation algorithms differ in the way they use multiple epi-
. Different estimation algorithms differ in the way they use multiple epi-
polar constraint from multiple correspondence pairs.
4.3. Proposed Estimation Method
It is common to represent the rotation matrix by its Euler-angles:
![]() (6)
(6)
Given the relative rotation matrix, a set of points from the first image![]() ,
, ![]() , corres-
, corres-
ponding to a set of points from the other image![]() ,
, ![]() , where
, where ![]() for all i, the optimization problem is:
for all i, the optimization problem is:
![]() (7)
(7)
Using the Euler-angle representation, each corresponding pair![]() , yield one linear equation:
, yield one linear equation:
![]()
Hence, the optimization problem (7) is reduced to a 3-dimensional linear optimization problem:
![]() (8)
(8)
A valid solution is possible with only two equations because t has only 2 degrees of freedom. But to avoid degenerated situations we use it with a minimal set of 3 correspondences.
Similar to the 8-point algorithm [8] , if more than 3 point correspondences are available, the linear 3-point algorithm can be used to find a least squared solution to an over-constrained system (8).
4.4. Relative Orientation from Sensor Measurements
The rotation matrix in Equation (3) represents the rotation from the second camera to the first, where the first camera is located at the origin and is align with the coordinate system major axis. In case the rotation matrices of both cameras are given by sensor measurements with respect to some global reference frame, the relative orientation need to be computed for the proposed algorithm. Let ![]() and
and ![]() be the rotation matrix and the translation vector of the first camera and
be the rotation matrix and the translation vector of the first camera and![]() ,
, ![]() are the same parameters of the second camera, then the relative pose can be computed as:
are the same parameters of the second camera, then the relative pose can be computed as:
![]() (9)
(9)
![]() (10)
(10)
Then, ![]() is separated to its Euler-angle representation which are used to compute the linear coefficients of the constraints in (8). Equation (10) is used to compute the actual location based on the estimated
is separated to its Euler-angle representation which are used to compute the linear coefficients of the constraints in (8). Equation (10) is used to compute the actual location based on the estimated![]() .
.
5. Image Interpolation for Virtual Camera
A schematic illustration of the virtual camera problem is illustrated in Figure 2. Given the spatially calibrated cameras and 3D reconstructed points, the goal is to render the images of an artificial cameras moving along a specific trajectory. Each virtual image along this trajectory is reconstructed from the two most similar camera images. The camera similarity is defined according to the rotation deviation of the neighbor cameras.
After identifying the two most suitable cameras, our approach for novel view image synthesis consists of the following steps:
1) Projection of feature correspondences from two nearest views into new image.
2) Delaunay triangulation of projected points.
3) Warp triangles into new view.
4) Fill holes and background from a background model.
The following subsections detail our approach with respect to the processing steps.
5.1. Feature Projection on New View and Triangulation
For a new camera pose, i.e., 3D rotation and spatial location, we commence by identifying the two closest cameras, and the subset of 3D points that corresponds to matching feature pairs. The two cameras are the two that have the most similar orientation out of the set of nearby cameras. This stage utilizes the 3D background model that been constructed in the spatial calibration task.
Using the epipolar constraint and guided matching more features pairs are added and triangulated, where the triangulation procedure is the standard Delaunay triangulation. An example of the pairwise matching and the projection on the new view is given in Figure 3.
5.2. Triangle Warp
The triangulation on the new view induce triangular meshes on the two existing images. In the next phase we sequentially go over the triangles in the new view and render them one at a time.
In order to choose the best “looking” triangle we compute the Procrustes distance [33] [34] between the triangle in the new view and the corresponding triangles in the two chosen images. The Procrustes distance, ![]() , is a geometrical similarity measure between two shapes, U and V, with k points represented by a configuration matrix
, is a geometrical similarity measure between two shapes, U and V, with k points represented by a configuration matrix![]() . In our application, we compare triangles in the plane, hence k = 3 and m = 2.
. In our application, we compare triangles in the plane, hence k = 3 and m = 2.
A normalization procedure precedes the computation of the Procrustes distance. The centroid of the configuration is translated to the origin and the norm of the configuration is rescaled to unity. The distance is defined as:
![]()
Figure 2. A schematic illustration of the virtual camera problem. Given a set of calibrated cameras and a set of 3D reconstructed points, we aim at generating the images of an artificial camera moving along the green line. In the proposed scheme, each new image is reconstructed from two images taken from the two most similar cameras.
![]()
![]()
![]() (a) (b) (c)
(a) (b) (c)
Figure 3. (a) Dense matching between two existing images; (b) Corresponding 3D points are projected on the new camera image; (c) The feature points on the new empty images are triangulate using standard Delaunay triangulation.
![]() (11)
(11)
where ![]() are the singular values of
are the singular values of![]() . The full derivation of this result can be found in ([33] , Ch. 4).
. The full derivation of this result can be found in ([33] , Ch. 4).
We add another condition on the appearance of the triangles if the sum of squared difference (SSD) of the pixels from the two triangle is above a predifined threshold we reject this specific triangle. This condition, has two proposes. First, it aims to handle matching errors, that can reduce appearance artifacts. Second, it reduces the artifacts caused by triangle that its pixels cover segments in multiple depths.
5.3. Min-Cut Blending
Each new rendered triangle is expanded by a constant band that overlaps the already rendered pixels. Similar to image quilting [35] , we apply dynamic programming to compute a path through the error surface at the overlap area. The error values are just the SSD values between the new triangle and the existing pixels. This procedure reduces hard boundaries between the triangles. Figure 4 depicted two examples of the final boundaries between the new render triangle and the existing pixels.
6. Experimental Results
In this section we provide a quantitative evaluation of the proposed approach on synthetic generated data as well as on several real-world datasets. These evaluations show that the presented algorithm leads to estimators that are competitive with state-of-the-art algorithms.
6.1. Synthetic Data
In this experiment we synthesized 3D data points and two cameras with known poses and intrinsic parameters. We report two kinds of experiments, the first examine the resilience of the estimation algorithm to additive spatial noise that perturbed the feature points in the image domain. The second experiment, examine the behavior of the estimation algorithm in the presence of mis-matched points, i.e., in the presence outliers. For the synthetic
![]()
![]() (a) (b)
(a) (b)
Figure 4. To reduce hard boundaries we compute a soft boundary (depicted in red) as the minimum cost path through the error surface at the overlap region. The overlap region is the green triangle.
experiment we compared our algorithm to the standard normalized-8-points algorithm (N8P) [8] and to the implementation of the 5-pt algorithm given by [36] .
For each experiment we test 3 camera configurations. First, two cameras with the same orientation looking forward located along the x-axis. Second, two cameras located along the x-axis looking forward with different orientations. Third, the two cameras located one in front of the other, with the same orientation.
We report two evaluation criteria. First, the root mean square error (RMSE) on the basis of the Sampson distance, which is defined as:
![]() (12)
(12)
where ![]() and
and![]() . In addition,
. In addition, ![]() and
and![]() , k = 1, 2, denote the square of the k-th element of
, k = 1, 2, denote the square of the k-th element of ![]() and
and![]() , respectively. The Sampson distance is an estimate to the reprojection error, and it is a popular alternative since it is much easier to evaluate. This is measured on a small validation set of noise-free points. The second criterion is the error of the translation vector estimator with respect to the ground-truth.
, respectively. The Sampson distance is an estimate to the reprojection error, and it is a popular alternative since it is much easier to evaluate. This is measured on a small validation set of noise-free points. The second criterion is the error of the translation vector estimator with respect to the ground-truth.
The results of the experiments are illustrated in Figure 5 and Figure 6, for the outliers and spatial noise tests, respectively. It is evident that the proposed algorithm outperform the other algorithms for both the spatial noise test and the outliers contamination test.
6.2. Real Data
We evaluate the propose calibration approach on two benchmark datasets that are extensively used for evaluating structure-from-motion algorithms [37] . Each image is of size 2048 × 3072 and has been corrected for distortion.
Both datasets are available online3, and include accurate camera matrices from which we extract the rotation matrices. The first dataset is the Fountain-P11, which contains eleven images of a fountain. The other dataset is the Herz-Jesu-P25 which contain 25 images of a building. Feature points were detected using standard corner detector and were described by SIFT descriptors [7] . Then, we compute putative matching by descriptor similarities and imposing mutual matching. These correspondences with the calibration matrices and the rotation matrices were the input to a RANSAC-based calibration algorithm. In each iteration of the algorithm a 3-point set of correspondences were sampled and used to solve the optimization problem prsented in Equation (8). The iterative process continued until a valid set is found which separate the correspondence set into inliers and outliers. The final estimation result is given by solving Equation (8) using all the inliers set.
The estimated camera locations and the estimated 3D structure of both datasets are illustrated in Figure 7.
In addition, we compare the camera location estimates of the proposed algorithm to the results reported by Dalalyan and Keriven [26] . As stated above, they proposed a global estimator for the same problem, i.e., spatial calibration in case of known rotation angles. They also published their Matlab code with their data matrices for both datasets4. The accuracy and timing performance of our algorithm compared to their algorithm both running implemented in Matlab and given the same input is reported in Table 1 for the Fountain-P11 dataset, and in Table 2 for the HerzJesu-P25 dataset. While the estimation error for the Fountain-P11 dataset is comparable to Dalalyan and Keriven [26] algorithm, the timing of the proposed algorithm is an order of magnitude better. For the HerzJesu-P25 dataset both the timing of the proposed algorithm is an order of magnitude better where the accuracy is two order of magnitude better.
This experiments on real datasets provided both qualitative and quantitative results that prove the validity of the proposed algorithm for solving spatial calibration problems.
![]()
![]() (a) (b)
(a) (b)
Figure 7. Camera locations and scene points estimated by the proposed 3-pt algorithm. (a) Fountain-P11 dataset; (b) HerzJesu-P25 dataset.
![]()
Table 1. Numerical results comparing the performance of the proposed algorithm with respect to the method reported in [26] on the Fountain-P11 dataset. Both algorithms were implemented in Matlab and run on the same data.
![]()
Table 2. Numerical results comparing the performance of the proposed algorithm with respect to the method reported in [26] on the HerzJesu-P25 dataset Both algorithms were implemented in Matlab and run on the same data.
6.3. Virtual Camera
In this section we demonstrate the validity of the proposed virtual camera scheme. The reported results are based on the Fountain-P11 dataset, more results are available in the project’s website5. We applied the spatial registration algorithm (Section 4) and reconstructed the 3D point cloud as is illustrated in Figure 7. The artificially trajectory was defined as a smooth path from the first camera to the last that goes through the centroid of the camera locations. This is the green path depicted in Figure 2.
Synthetic image is presented in Figure 8 (middle column) with respect to the two existing images that been used as “building material” (left and right columns). It is clear that the produced synthetic image is perceptually a convincing image. There are, though, some artifact yielded by the perspective changes between the two views, e.g., in the water pipe behind the fountain and the image border. These are expected artifacts since generating a novel image is an ill-posed problem due to change in perspective and occlusions. An interesting results is shown in the bottom row depicting a zoomed-in part of the images above. The synthesized image in the middle looks convincing enough, except from a small curvature behind the statue’s head that is caused by the perspective change and the limited information.
7. Conclusions
These days, given the amount of images and videos capture of the same scene at the same time, it is natural to ask, how all this huge volume of information can be utilized for a different and better experience for the user? In this paper we present two algorithms that can be the first building blocks for such an ambitious goal.
The first algorithm is a spatial calibration algorithm, which gives the captures images and the measurements of the device’s sensors accurately and efficiently estimates the pose of the cameras. We validate the proposed algorithm on synthetically generated data and on well-established benchmark datasets, and compare it to state- of-the-art algorithms.
The second algorithm is a virtual images generator that gets the calibrated cameras poses and the reconstructed 3D point cloud, and generates virtually appealing images of a virtual camera moving along a specific trajectory. The proposed algorithm generates the virtual image from two images of the cameras that have similar viewing angle and are not far from the virtual camera. We present several results that demonstrate the quality of the algorithm.
Acknowledgements
The authors gratefully acknowledge the support by the European Union under the 7th Research Framework, programme FET-Open SME “SceneNet” (GA 309169).
NOTES
1The SceneNet project, programme FET-Open SME (GA 309169), http://scenenet.uni-bremen.de/.
![]()
2Note that using the 5-point algorithm [9] demand 146 iterations, but the computational complexity of each iteration is much higher.
![]()
3http://cvlabwww.epfl.ch/data/multiview/denseMVS.html.
4http://imagine.enpc.fr/dalalyan/3D.html.
![]()
5http://scenenet.uni-bremen.de/.