1. Introduction
In 1935, Einstein, Podolsky, and Rosen published their famous EPR paper, which posited that the quantum mechanical wave function did not provide a complete description of physical reality ([1] , p. 78). However, the EPR paper was factually written by Podolsky, who had submitted the paper without Einstein’s validation. Einstein complained about the EPR paper to Schrödinger, stating, “the essential thing was smothered by the formalism” ( [2] , p. 35). Consequently, Einstein discussed the EPR experiment again and presented the following dilemma [3] :
1) Quantum mechanics is incomplete, or
2) Quantum mechanics is nonlocal.
This dilemma is at the heart of the EPR experiment. In what follows, we call this dilemma the “Einstein Dilemma” after Redhead ( [4] , p. 76). Einstein preferred to believe in the incompleteness of quantum mechanics because, in his words,
The total rejection of this principle [principle of action through a medium] would make impossible the idea of the existence of a (quasi-) closed system, and thereby also make impossible the establishment of empirically verifiable laws in our well-known sense ( [5] , p. 322) (Author’s translation).
Bohr published a paper with the same title as the EPR paper and rebutted the EPR argument [6] . Bohr admitted that “there is, in a case like that, just considered no question of a mechanical disturbance of the system under investigation during the last critical stage of the measuring procedure,” but insisted that “even at this stage, there is essentially the question of an influence on the very conditions which define the possible types of predictions regarding the future behavior of the system”.
There are many views on Bohr’s statement [7] - [11] . However, I believe that regardless of the view taken into consideration, Bohr’s argument still could not have circumvented the Einstein Dilemma. Before we discuss Bohr’s view, we have to clarify the meaning of the word “locality”. Redhead suggests five types of locality that we use in the field of quantum mechanics ( [4] , p. 77, 82); however, only three of these are related to our dis- cussion:
 An unsharp value for an observable cannot be changed into a sharp value by measurements performed “at a distance.”
An unsharp value for an observable cannot be changed into a sharp value by measurements performed “at a distance.”
 A previously undefined value for an observable cannot be defined by measurements performed “at a distance.”
A previously undefined value for an observable cannot be defined by measurements performed “at a distance.”
 A sharp value for an observable cannot be changed into another sharp value by altering the setting of a remotely located apparatus.
A sharp value for an observable cannot be changed into another sharp value by altering the setting of a remotely located apparatus.
Redhead speculates that the locality in the Einstein Dilemma can be described with 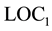 and that the locality in Bohr’s “complementarity” can be described with
and that the locality in Bohr’s “complementarity” can be described with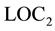 . Therefore, Bohr’s interpretation could cir- cumvent the Einstein Dilemma because
. Therefore, Bohr’s interpretation could cir- cumvent the Einstein Dilemma because  does not change real situation. Redhead discussed that the locality
does not change real situation. Redhead discussed that the locality 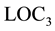 appears in Bell’s theorem.
appears in Bell’s theorem.
In this work, I show that the existing interpretations of quantum mechanics, including that of Bohr, must be subject to the Einstein Dilemma (Section 2); further, I provide a new interpretation that makes it possible to circumvent the dilemma (Sections 3 and 4).
2. Einstein Dilemma and Complementarity
First, let us examine Redhead’s view that Bohr’s locality is equivalent to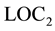 . If this is true, we consider whether Bohr’s conclusion can overcome the dilemma.
. If this is true, we consider whether Bohr’s conclusion can overcome the dilemma.
Let us consider Bohm’s version of the EPR experiment ( [12] , pp. 611-615). Two electrons (I and II), which initially interact with each other at  and whose total spin value is zero, spatially move apart. When the x-spin of electron I is measured at t
and whose total spin value is zero, spatially move apart. When the x-spin of electron I is measured at t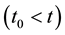 , we can predict the value of the x-spin of electron II with certainty.
, we can predict the value of the x-spin of electron II with certainty.
If 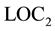 is violated, the
is violated, the 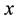 -spin of electron II is defined by the measurement of the x-spin of electron I. Redhead argues that the violation of
-spin of electron II is defined by the measurement of the x-spin of electron I. Redhead argues that the violation of  does not mean the violation of
does not mean the violation of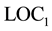 , but is this correct? Defining the spin value of electron I does not guarantee that the x-spin of electron II has a sharp value. However, we can predict the x-spin of electron II with certainty after t, and thus, the x-spin has a sharp value. This result suggests that if we accept the violation of
, but is this correct? Defining the spin value of electron I does not guarantee that the x-spin of electron II has a sharp value. However, we can predict the x-spin of electron II with certainty after t, and thus, the x-spin has a sharp value. This result suggests that if we accept the violation of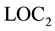 , we also have to accept the violation of
, we also have to accept the violation of . Therefore, we can con- clude that Redhead’s version of Bohr’s interpretation is subject to the Einstein Dilemma.
. Therefore, we can con- clude that Redhead’s version of Bohr’s interpretation is subject to the Einstein Dilemma.
We now examine other views of Bohr’s interpretation. Beller and Fine discuss that Bohr adopted positivism as his philosophy of science after the EPR paper was published [7] [8] . If Beller and Fine are considered to be correct, this indicates that quantum mechanics violates![]() , and thus, Bohr’s interpretation is still subject to the dilemma.
, and thus, Bohr’s interpretation is still subject to the dilemma.
Those familiar with this controversy might consider that Bohr’s interpretation could circumvent the dilemma if the view of Howard, Halvorson-Clifton, and Ozawa-Kitajima (HHCOK) of Bohr’s interpretation is correct [9] - [11] . HHCOK speculate that the word “classical” as used by Bohr refers to the mixture state and that the experimental setup determines how a pure state changes into the mixture state. We can say that (according to HHCOK) Bohr introduces “nonseparability” instead of “nonlocality” (see also [13] ).
According to the HHCOK version of Bohr’s view, before the measurement of electron I, the states of the electrons are the mixture states of the x-spin. It should be noted, however, that the mixture state of the x-spin is not the eigenstate of the x-spin, and thus, we cannot predict which value the x-spin would assume using only quantum mechanics. This assumption suggests that we have to choose one of the following options:
1) The x-spin has a sharp value before the measurement. It follows that quantum mechanics is incomplete because it cannot predict which value the x-spin would have before measurement (since the mixture state is not the eigenstate).
2) The x-spin has an unsharp value before the measurement. It follows that quantum mechanics violates LOC1 because the spin of electron II can have a sharp value only after the measurement of the spin of electron I.
Therefore, the HHCOK version of Bohr’s interpretation of quantum mechanics will also face the Einstein Dilemma. Accordingly, it does not matter which view of Bohr’s interpretation we consider, we cannot reject either part of the dilemma. Next, we examine the existing interpretations of quantum mechanics other than Bohr’s interpretation.
HHCOK speculate that Bohr’s interpretation does not accept the projection postulate. If we consider an interpretation that assumes the projection postulate, it follows that quantum mechanics is nonlocal (violation of![]() ). The de Broglie-Bohm interpretation concludes that quantum mechanics is incomplete (and nonlocal- violation of
). The de Broglie-Bohm interpretation concludes that quantum mechanics is incomplete (and nonlocal- violation of![]() ).
).
The many-worlds interpretation (MWI) postulates that quantum mechanics is nonlocal. Some readers might believe the MWI avoids the issue of nonlocality. Nevertheless, because the worlds split for a very short period of time, we cannot avoid nonlocality [14] . Although this interpretation does not necessarily mean the violation of localities ![]() -
-![]() , it does mean that the real situation is widely changed for a very short period of time. Einstein’s meaning of “nonlocal” is the action that telepathically changes the real situation ( [3] , p. 322) ( [5] , p. 85), and thus, the MWI is also subject to the Einstein Dilemma.
, it does mean that the real situation is widely changed for a very short period of time. Einstein’s meaning of “nonlocal” is the action that telepathically changes the real situation ( [3] , p. 322) ( [5] , p. 85), and thus, the MWI is also subject to the Einstein Dilemma.
Next, we consider whether it is impossible to avoid the Einstein Dilemma. In the remainder of this paper, I suggest an interpretation that circumvents the dilemma. This interpretation is based on one of the formalisms of quantum mechanics, known as “two-state vector formalism (TSVF),” as proposed by Aharonov, Bergmann and Leibowitz (ABL) [15] . I briefly summarize TSVF in Section 3, and I show how the new interpretation makes it possible to circumvent the Einstein Dilemma in Section 4.
3. Brief Review of Two-State Vector Formalism
In this section, I briefly summarize TSVF. In conventional quantum mechanics (CQM), only the past state determines the probability that a physical quantity Q has a certain value ![]() (the Born rule). In contrast, in TSVF, both the past and the future states determine the probability that Q has a certain value
(the Born rule). In contrast, in TSVF, both the past and the future states determine the probability that Q has a certain value![]() . The ABL rule is used for determining the probability from the past and the future states [15] .
. The ABL rule is used for determining the probability from the past and the future states [15] .
Assume that Q has eigenstates![]() , which, respectively, have eigenvalues
, which, respectively, have eigenvalues ![]() (assume that there is no degeneracy). The probability,
(assume that there is no degeneracy). The probability, ![]() , that Q has a value
, that Q has a value ![]() at
at ![]() is calculated as follows using the ABL rule:
is calculated as follows using the ABL rule:
![]() (1)
(1)
Here,
![]() (2)
(2)
where ![]() denotes the initial state of the system measured at
denotes the initial state of the system measured at![]() , and
, and ![]() denotes the final state of the system measured at
denotes the final state of the system measured at![]() , where
, where![]() .
.
At times, the probabilities calculated using the ABL rule differ from those calculated using the Born rule. It appears as if TSVF and CQM are different theories, although they are not. The ABL rule agrees with the Born rule when ![]() in Equation (1) changes to
in Equation (1) changes to![]() ; this implies that TSVF agrees with CQM when we consider only the past state.
; this implies that TSVF agrees with CQM when we consider only the past state.
There seems to be no method for verifying the prediction made using TSVF because we cannot know the intermediate state at t without destroying the state. Aharonov, Albert and Vaidman solved this problem by pro- posing a new measurement concept called ‘weak measurement’; measurements made according to this concept do not destroy the intermediate quantum state [16] . In the remainder of this paper, we refer to the conventional measurement as ‘strong measurement’.
According to Aharonov, Albert and Vaidman [17] , the mean value obtained by weak measurement is the “weak value”. The weak value of the physical quantity Q at![]() ,
, ![]() , is
, is
![]() (3)
(3)
Recently, physicists performed a weak measurement and confirmed that the theoretically predicted and mea- sured weak values showed good agreement [18] .
4. Einstein Dilemma and Two-State Vector Formalism
In general, when the final state is an eigenstate, ![]() , of Q, the intermediate state is also
, of Q, the intermediate state is also ![]() with certainty because
with certainty because
![]() (4)
(4)
Thus, the physical quantity has a sharp value even before the measurement. In this paper, I do not consider the case where the final state is not an eigenstate. Consider Bohm’s version of the EPR experiment. When the interaction between two electrons ends at![]() , the state of the whole system is
, the state of the whole system is
![]() (5)
(5)
where ![]() and
and ![]() represent the states in which the measured values of the
represent the states in which the measured values of the ![]() -spin are
-spin are ![]() and
and![]() , respectively (unit is
, respectively (unit is![]() ). When the x-spin of electron I is measured at
). When the x-spin of electron I is measured at ![]() and the value is
and the value is![]() , the state of the system becomes
, the state of the system becomes
![]() (6)
(6)
From the ABL rule (1), the probability that the state of the system at a given time ![]()
![]() is
is ![]() is 1. Therefore, the values of the x-spin of electrons I and II are
is 1. Therefore, the values of the x-spin of electrons I and II are ![]() and
and![]() , respectively, subsequent to the end of the interaction.
, respectively, subsequent to the end of the interaction.
It follows from this result that we do not need to assume any type of nonlocality. Furthermore, quantum mechanics is not modified. Accordingly, we can simultaneously insist that quantum mechanics is complete and local. Here, we can avoid confronting the Einstein Dilemma.
Readers might suspect that using TSVF means that quantum mechanics is not complete because the final state can be considered a “hidden variable.” Actually, it depends on the definition of the hidden variable. For example, the de Broglie-Bohm interpretation needs hidden variables of both position and momentum because we can clearly interpret that quantum mechanics does not need both position and momentum.
However, it is not always clear whether the final state is a hidden variable, unlike the case with the de Broglie-Bohm interpretation. TSVF formalism does not modify quantum mechanics because TSVF considers the description of the state vector as complete, but we need two state vectors for completeness. TSVF does not require adding any other variables other than the state vector. Therefore, I insist that quantum mechanics is still complete if my interpretation using TSVF is correct.
Nevertheless, this interpretation still appears problematic in the following situation. Let us assume that we measure the z-spin of an electron at ![]() and obtain a value
and obtain a value![]() ; thus, the system state is
; thus, the system state is![]() . Thereafter, we measure the x-spin of the electron at
. Thereafter, we measure the x-spin of the electron at ![]() and obtain a value
and obtain a value![]() ; thus, the system state is
; thus, the system state is![]() .
.
According to the ABL rule, both the probability that the system state at ![]()
![]() is
is ![]() is 1 and the probability that the system state at
is 1 and the probability that the system state at ![]() is
is ![]() is 1. However, a quantum system cannot have eigenstates of both
is 1. However, a quantum system cannot have eigenstates of both ![]() -spin and
-spin and ![]() -spin simultaneously. Let us assume that the state of a system
-spin simultaneously. Let us assume that the state of a system ![]() is an eigenstate of non-commutative observables
is an eigenstate of non-commutative observables ![]() and
and ![]() having eigenvalues
having eigenvalues ![]() and
and![]() , respectively. Consequently,
, respectively. Consequently,
![]() (7)
(7)
This contradicts the assumption that ![]() and
and ![]() are non-commutative. Therefore, Aharonov, Popescu, and Tollaksen state the following:
are non-commutative. Therefore, Aharonov, Popescu, and Tollaksen state the following:
If at t we measure the spin in the z-direction, we must find it up, because that’s how the particle was prepared at![]() . On the other hand, if at t we measure the spin along x, we must also find it up, because otherwise the measurement at
. On the other hand, if at t we measure the spin along x, we must also find it up, because otherwise the measurement at ![]() wouldn’t find it up ( [19] , p. 27).
wouldn’t find it up ( [19] , p. 27).
Nonetheless, there is still concern that our interpretation contradicts the uncertainty relation (Kennard-Robertson inequality). Let us assume that an ensemble of electrons whose z-spin at ![]() is
is ![]() and
and ![]() -spin at
-spin at ![]() is
is ![]() has been prepared, and let us divide the ensemble into two sub-ensembles:
has been prepared, and let us divide the ensemble into two sub-ensembles: ![]() and
and![]() . When we per- form weak measurement of the
. When we per- form weak measurement of the ![]() -spin in
-spin in ![]() and the z-spin in
and the z-spin in ![]() at t, we would obtain the result that the x-spin is
at t, we would obtain the result that the x-spin is ![]() and z-spin is
and z-spin is ![]() with certainty. This result indicates that both the standard deviations of x-spin in
with certainty. This result indicates that both the standard deviations of x-spin in ![]() and z-spin in
and z-spin in ![]() are 0. This result appears to contradict the uncertainty relation.
are 0. This result appears to contradict the uncertainty relation.
However, it is to be noted that the uncertainty relation considers only the past state. In our interpretation, we consider the future state as well, thus it is no problem to contradict with the uncertainty relation.
Here, we define new standard deviation of z-spin for our interpretation as
![]() (8)
(8)
where ![]() denotes an operator of
denotes an operator of ![]() -spin. Consequently, we can easily obtain
-spin. Consequently, we can easily obtain
![]() . (9)
. (9)
Likewise, we can obtain![]() . Therefore, when we interpret
. Therefore, when we interpret ![]() as the standard deviation of
as the standard deviation of ![]() - spin in TSVF, it is not starange that both of the standard deviations of x-spin in
- spin in TSVF, it is not starange that both of the standard deviations of x-spin in ![]() and z-spin in
and z-spin in ![]() are 0.
are 0.
In general, when we define
![]() (10)
(10)
where ![]() is an observable quantity,
is an observable quantity, ![]() represents an eigenstate of
represents an eigenstate of![]() , and
, and![]() , we can easily obtain
, we can easily obtain
![]() (11)
(11)
when the final state is an eigenstate of![]() .
.
Nevertheless, there remains the concern that the abovementioned interpretation may contradict no-go theorem such as the Kochen-Specker theorem [20] . However, we can easily infer from Mermin’s version of the Kochen- Specker theorem that there might not be any contradiction when only x-spin and z-spin are determined because the Kochen-Specker theorem holds only when more than two axes of spin are determined [21] .
In addition, Tollaksen discusses that the weak value of spin changes according the context of the experiment [21]
[22] . For example, he shows that there is a case where![]() , even though
, even though ![]() and
and
![]() , where
, where ![]() represents the weak value of
represents the weak value of ![]() -spin
-spin ![]() of particle
of particle ![]()
![]() .
.
5. Conclusions
Upon his examination of quantum mechanics in the EPR paper, Einstein was presented with the dilemma that
1) Quantum mechanics is incomplete, or
2) Quantum mechanics is nonlocal.
Most physicists choose the nonlocality of quantum mechanics over Einstein’s choice of incompleteness. However, if possible, it is better to reject both choices.
According to TSVF, physical quantities can have sharp values before measurement. Therefore, we do not need to introduce the concept of nonlocality. Furthermore, TSVF does not assume any hidden variables; thereby ensuring that quantum mechanics is complete. In conclusion, we circumvented the Einstein Dilemma by con- sidering both the past state and the future state of a quantum mechanical system.
Acknowledgements
This work has been supported by Japan Society for the Promotion of Science (Grant No. 26370021).