The Interacting Generalized Ricci Dark Energy Model in Non-Flat Universe ()
1. Introduction
The current astrophysical observations of the Type Ia supernovae (SNIa) [1] [2] , the cosmic microwave background (CMB) [3] -[10] and the large scale structure (LSS) [11] have revealed that the expansion of our universe is accelerated [1] [2] . This indicates that there exists some unknown energy, called dark energy, to realize the accelerated expansion. The simplest interpretation of dark energy is the cosmological constant. However, this model requires an incredible fine-tuning, since the observed cosmological constant is extremely small compared to the fundamental Planck scale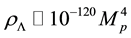
. Also, this model suffers from the cosmic coincidence problem: why the cosmological constant and matter have comparable energy density today even though their time evolution is so different.
Among various attempts to solve these problems, we focus on the holographic dark energy (HDE) models [12] motivated by the holographic principle of quantum gravity [13] -[16] . Requiring that the total vacuum energy of a system with size L would not exceed the mass of the black hole of the same size, the dark energy density is proposed as
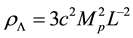(1)
where c is a dimensionless parameter,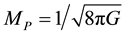 
is the reduced Planck mass. As for the size L, which is regarded as an IR cutoff, various possibilities are discussed in literatures, such as the Hubble parameter L−1 = H [12] , the future event horizon 
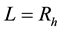[12] , the age of our universe L = T [17] , and the Ricci scalar curvature 
[18] . With a reasonable choice of L, Equation (1) naturally explains the observed value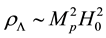 
(
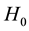is the present Hubble parameter). In our previous work [19] , we studied the Ricci dark energy (RDE) model with 
by introducing an interaction between dark energy and matter. It was shown that a nonvanishing interaction rate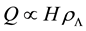 
is favored by the observations [19] .
In this paper, we extend our previous analysis, and consider the interacting RDE (IRDE) model in non-flat universe. This paper is organized as follows. In Section 2, we describe the generalized IRDE model in non-flat universe, and obtain analytic expressions for cosmic time evolution. In Section 3, we discuss the observational constraints on this model. We summarize our results in Section 4.
2. The Interacting Ricci Dark Energy Model
We study the interaction Ricci Dark Energy (IRDE) model in non-flat universe. The Friedmann-Robertson- Walker metric non-flat univrerse is given by
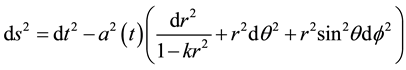(2)
where k = 1, 0, −1 for closed, flat, and open geometries. The Friedmann Equation in non-flat univrerse takes the form
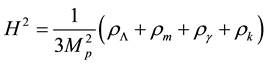(3)
where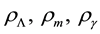 
and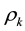 
represent energy density of dark energy, matter, radiation and curvature, respectively, and 
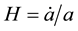is the Hubble parameter.
We generalize the energy density of the Ricci dark energy as
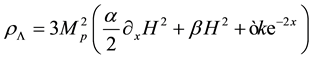(4)
where α, b and ![]()
are dimensionless parameters and![]()
. In the case of![]()
, ![]()
, ![]()
, this model is reduced to the ordinary RDE model [19] . Moreover, we introduce a phenomenological interaction between dark energy and matter. The energy densities ![]()
and ![]()
obey the following Equations [20] -[40]
![]()
(5)
![]()
(6)
We adopt the interaction rate given by
![]()
(7)
where ![]()
is a dimensionless parameter [19] . To solve H, combining with Equations (4) and (6), the Friedmann Equation (3) is transformed as
![]()
(8)
The solution to Equation (8) is given by
![]()
(9)
where
![]()
(10)
![]()
, ![]()
and![]()
. When ![]()
can be imaginary for sufficiently large α, b and γ, ![]()
has oscillatory behavior [19] . The constants![]()
, ![]()
and ![]()
are obtained as
![]()
(11)
![]()
(12)
![]()
(13)
In the case of![]()
, ![]()
and![]()
, Equation (9) reduces to the result obtained in our previous work [19] . Substituting Equation (9) to Equation (4), the Ricci dark energy density is obtained as
![]()
(14)
where![]()
, ![]()
, Likewise, the matter density is obtained as
![]()
(15)
To derive the Equation of state parameter ![]()
of the Ricci dark energy, substituting Equation (14) into the following expression:
![]()
(16)
3. Observational Constraints
In this section, we discuss cosmological constraints on the IRDE model in the non-flat universe ![]()
obtained from SNIa, CMB, BAO and the Hubble parameter observations.
The luminosity distance in the non-flat universe can be written as
![]()
(17)
The SNIa observations measure the distance modulus μ of a supernova and its redshift z. The distance modulus is given by
![]()
(18)
We use the Union data set of 580 SNIa [41] [42] to obtain limits on the relevant parameters α, γ and ![]()
by minimizing ![]()
[43] -[46] .
The CMB shift parameter R is given by
![]()
(19)
where ![]()
is the redshift at recombination, and ![]()
is the matter fraction at present. We use the value ![]()
obtained from the WMAP9 data [3] -[10] . The CMB constraints are obtained by minimizing ![]()
[43] -[46] . The shift parameter gives a complementary bound to the SNIa data![]()
, since this parameter involves the large redshift behavior![]()
.
Signatures of the baryon acoustic oscillation (BAO) are provided by the observations of large-scale galaxy clustering. The BAO parameter A is defined by
![]()
(20)
where![]()
. We use the measurement of the BAO peak in the distribution of luminous red galaxies (LRGs) observed in SDSS [11] :
![]()
(21)
The BAO constraints are obtained by minimizing ![]()
[43] -[46] .
The Hubble parameter constraints are given by minimizing
![]()
(22)
where ![]()
is the 1σ uncertainty of the observational ![]()
data [47] -[52] .
In Figure 1, we plot the Equation of state parameter ![]()
for ![]()
(blue), 0 (red) and 0.1 (green) as a function of the scale factor![]()
. The dotted and solid lines are the results for the case without interaction ![]()
and with interaction![]()
, respectively. The dark energy parameter is fixed as![]()
. Though the
value ![]()
is too large (see Figure 2), we use these values to visualize the effect of the curvature in the figure. In the case of the curvature![]()
, the value of w is larger than another case, but the condition for accelerated expansion at present ![]()
is satisfied for each cases.
In Figure 3, we plot the evolution of the energy density fractions Ω for radiation (green), matter (red) and dark energy (blue) for![]()
. The dotted and solid lines are the results for the case without interaction ![]()
and with interaction![]()
, respectively. The panels (a), (b) and (c) corresponds to![]()
, −0.1 and 0.1, respectively. One can see that the effect of the curvature can be important only for![]()
. The fractions ![]()
and ![]()
for ![]()
in the panel (b) (![]()
in the panel (c)) are slightly increased (decreased) around ![]()
compared to the flat case (a). Around radiation-matter equality, the radiation component ![]()
is increased by several percents compared to the corresponding result without interaction (dotted line), while the ![]()
is decreased due to the interaction.
4. Conclusion
We have considered the IRDE model in the non-flat universe. We have derived the analytic solutions for the
Hubble parameter (9), the dark energy density (14) and matter energy density (15). We have also studied astrophysical constraints on this model using the recent observations including SNIa, BAO, CMB anisotropy, and the Hubble parameter. We have shown that the allowed parameter range for the fractional energy density of the curvature is ![]()
for![]()
. The best fit values with 1σ error are ![]()
and ![]()
with![]()
. We have shown that the IRDE model with a small curvature is allowed by observational constraints. Without the interaction, the flat universe is observationally disfavored in this model.
Acknowledgements
We would like to thank T. Nihei for his valuable discussion, helpful advice and reading the manuscript.
NOTES
*Corresponding author.