1. Introduction
The starting point of oligopoly theory is the static Cournot model. It provides an example of Nash equilibrium and embeds a variety of possible market outcomes. One is the Cournot Limit Theorem, which states that the Cournot-Nash equilibrium is the monopoly outcome in a market with one firm, and approaches the competitive equilibrium as the number of competitors approaches infinity1.
More sophisticated oligopoly models consider cases where firms interact over time. For example, in a Cournot-type supergame where the Cournot game is repeated in every period from now to eternity, an appropriately defined trigger strategy can support cooperation in every period (Friedman [3] ). Other models are dynamic because firms are slow to change their strategic variables, causing it to take time for firms to reach equilibrium. This can occur when change is costly, which forces firms into a differential oligopoly game. In cases such as these, the strategic variable (output or price) evolves to a limiting outcome that differs from the static Nash equilibrium that would occur if the change was instantaneous (i.e., the cost of change is zero). For example, Driskill and McCafferty [4] found that when output was slow to change in a Cournot-type game, the limiting output level fell between the static Cournot and perfectly competitive outcomes2.
In this paper, our goal is to extend the dynamic Cournot model to include management errors. Brownian motion is used to model these behavioral errors. To our knowledge, we are the first to incorporate Brownian motion into an oligopoly model. By adding this stochastic component, we are able to show that output converges to a random variable rather than a constant, as in the deterministic dynamic Cournot model. In the stochastic model, the limiting variance in firm output is smaller in duopoly than in monopoly. Finally, the stochastic model predicts that firm failure is more likely in smaller markets and for firms that are smaller in size and are less efficient at coping with behavioral errors. These results provide us with a better understanding of stochastic markets, in particular the exit patterns of firms when managerial errors are present.
The remainder of the paper is organized as follows. In Section 2 we summarize the deterministic model on which our stochastic model is built. In Section 3 we develop the stochastic version of the dynamic Cournot model by adding Brownian motion. Here, we derive the limiting distribution of the game and investigate the consequences of allowing one firm to be superior at coping with errors. In Section 4 we analyze the effect of management error on firm failure. The final section provides a brief conclusion.
2. The Deterministic Dynamic Model
Our stochastic model builds from a deterministic dynamic model that we develop in this section. Several scholars have investigated a dynamic version of the Cournot model. For example, Maskin and Tirole [6] considered a duopoly model that is made dynamic by requiring firms to alternatively choose their levels of output. Driskill and McCafferty [4] and Dockner [7] modeled dynamics by introducing a cost of adjusting firm output over time. In models such as these, firms have dynamic best-reply functions, such that a firm’s best reply depends on its own and its rival’s past output decisions. An important conclusion of these models is that the subgame perfect Nash equilibrium is more competitive than the static Cournot equilibrium. Because our stochastic model builds from the deterministic case, we first discuss a dynamic version of the deterministic Cournot model.
Consider a market with two firms (1 and 2) that produce homogeneous goods. The inverse demand function at
time t is linear: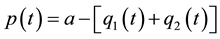 , where p is price,
, where p is price, 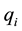 is firm i’s output level, and a is a positive constant. Firm i’s total cost of production is quadratic:
is firm i’s output level, and a is a positive constant. Firm i’s total cost of production is quadratic: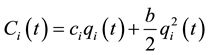 , where
, where  and b are positive con-
and b are positive con-
stants. In this model, firm inertia is motivated by the cost of changing its level of output. This adjustment cost is
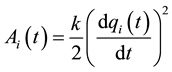 , where k > 0 is the adjustment cost parameter. Costs are assumed to be sufficiently low so
, where k > 0 is the adjustment cost parameter. Costs are assumed to be sufficiently low so
that both firms participate in this dynamic version of the game. At t = 0, each firm’s goal is to choose a production plan to maximize its discounted stream of profits:
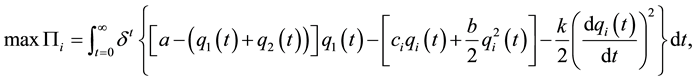 (1)
(1)
which is subject to the discount factor 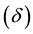 and the initial condition that the output of firm i in period 0 is
and the initial condition that the output of firm i in period 0 is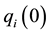 .
.
Dockner [7] solves this problem using dynamic programming methods. He showed that the solution depends on a set of dynamic best-reply functions, which are linear differential equations that are assumed to take the following form:
 (2)
(2)
 (3)
(3)
Parameter m is a function of the parameters of the model and represents firm i’s long-run sales target in the absence of firm j (i.e., firm i’s monopoly output). Parameter m will increase with the size of the market. These functions capture the strategic dynamics of the model. The solution to this system is:
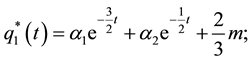 (4)
(4)
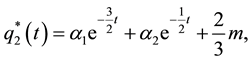 (5)
(5)
where 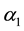 and
and 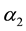 are determined by the initial conditions [
are determined by the initial conditions [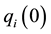 for i = 1 and 2]. Notice that as
for i = 1 and 2]. Notice that as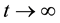 , a firm’s optimal level of output approaches
, a firm’s optimal level of output approaches![]() , regardless of the initial output of the two firms.
, regardless of the initial output of the two firms.
3. A Dynamic Cournot Model with Brownian Motion
In this section we add a stochastic component to the dynamic Cournot model of the previous section. The stochastic component derives from a behavioral error that influences the dynamic best-reply functions of firms. One potential cause is the presence of boundedly rational managers who make errors when attempting to identify the best course of action in a dynamic setting3. Such errors may result from the cognitive limitations of managers coupled with the time pressure to make quick decisions. In our setup, behavioral errors occur when managers implement the dynamic best-reply functions and are captured by Brownian motion4. Adding Brownian motion (Bt) to the dynamic best-reply Equations (2) and (3) and converting them to stochastic difference equations produces:
![]() (6)
(6)
![]() (7)
(7)
Equations (6) and (7) describe each firm’s updating strategy in output, which is impacted by three forces. The first is m, which represents the firm’s sales target. Firm i’s output will increases when![]() . The second force is rival output. As in the static Cournot model, firm i’s output falls with greater firm j output (i.e.,
. The second force is rival output. As in the static Cournot model, firm i’s output falls with greater firm j output (i.e., ![]() and
and ![]() are strategic substitutes). The last term captures the effect of positive or negative behavioral management errors on firm output. The distribution of these errors is the same for both firms, but one firm may be better at dealing with these errors than the other firm. This occurs when firms have different Brownian motion parameters (i.e.,
are strategic substitutes). The last term captures the effect of positive or negative behavioral management errors on firm output. The distribution of these errors is the same for both firms, but one firm may be better at dealing with these errors than the other firm. This occurs when firms have different Brownian motion parameters (i.e.,![]() ). Each parameter captures the magnitude of a firm’s behavioral error. For example, if managers do not make errors, then
). Each parameter captures the magnitude of a firm’s behavioral error. For example, if managers do not make errors, then ![]() and the model collapse to the deterministic dynamic model. If behavioral errors exist and firm 1 is superior at coping with these errors, then
and the model collapse to the deterministic dynamic model. If behavioral errors exist and firm 1 is superior at coping with these errors, then![]() .
.
Solving this system simultaneously produces a complex Gausian process, as described in Theorem 1.
Theorem 1: Given the game described above, the optimal paths of ![]() and
and ![]() are:
are:
![]() (8)
(8)
![]() (9)
(9)
Proof: See Appendix.
If![]() , then the difference in signs of the last set of terms in Equations (8) and (9) imply that
, then the difference in signs of the last set of terms in Equations (8) and (9) imply that![]() .
.
In the limit, the solutions to Equations (8) and (9) require Ito integration. This result is described in the next theorem.
Theorem 2: Characteristics of the limiting distribution of Equations (8) and (9) as t → ∞ are:
![]() (10)
(10)
![]() (11)
(11)
A comparison of the pair of Equations (4) and (5) with the equations in Theorem 2 reveals that unlike the deterministic Cournot model, ![]() does not converge to a constant but is now a random variable. In the deter-
does not converge to a constant but is now a random variable. In the deter-
ministic case, the optimal output level of each firm converges to![]() . With management error causing Brownian motion, the optimal level of output has a mean of
. With management error causing Brownian motion, the optimal level of output has a mean of![]() . Even with this business disturbance, the
. Even with this business disturbance, the
steady state equilibrium is the same on average as in the non-stochastic Cournot model. However, the stochastic model has a non-zero variance as seen in Equation (11). Another feature of the model is that the mean value in the model with Brownian motion does not depend on the initial positions of the two firms.
The final issue of interest is the effect of assuming that firm 1 is superior at dealing with behavior errors![]() . One might expect that firm 1’s limiting distribution would have a smaller variance. This is not the case, however, as the interaction effects across firms, as described in Equations (6) and (7), cause their distributions to converge to the same limit as
. One might expect that firm 1’s limiting distribution would have a smaller variance. This is not the case, however, as the interaction effects across firms, as described in Equations (6) and (7), cause their distributions to converge to the same limit as![]() .
.
To further analyze the effect of firm ability to cope with behavioral errors, consider the case where firms are equally capable (i.e.,![]() ). When this occurs, the limiting variance of each firm in Equation (11) be-
). When this occurs, the limiting variance of each firm in Equation (11) be-
comes![]() . One can see that the interaction effects reduce the limiting variance, by comparing the duopoly results with the monopoly result. The mean value of firm output equals
. One can see that the interaction effects reduce the limiting variance, by comparing the duopoly results with the monopoly result. The mean value of firm output equals ![]() in monopoly and equals
in monopoly and equals ![]() in
in
duopoly. With a single firm, the limiting variance in the single Orstein-Uhlenbeck mean-reverting equation
equals![]() , compared to a value of
, compared to a value of ![]() in the duopoly case5. A firm’s variance is smaller with more firms.
in the duopoly case5. A firm’s variance is smaller with more firms.
4. Behavioral Errors and Firm Failure
Firm failure is common in a free market economy. For example, Dunn et al. [10] found that approximately 80 percent of firms exit the market within 10 years of entry. This suggests that management inexperience that leads to errors is a likely cause of firm exit. In this section, we use a dynamic Cournot model with Brownian motion that is caused by management error to explain the exit process.
Consider a setting with the following characteristics. Assume an emerging market where firms enter by initially producing below their long-run optimal levels of output6. Firms are asymmetric, and firm 1 has the initial
strategic advantage, such that![]() . Firm exit occurs when
. Firm exit occurs when![]() ; once a firm exits, it
; once a firm exits, it
cannot re-enter the market in a later period7. From Equations (8) and (9), we know that the optimal output path for firm 1 is greater than that of firm 2. This suggests that firm 2 is more likely to fail than firm 1. In order to
simplify the analysis and focus on the importance of starting values, we assume that![]() .
.
With these assumptions and by defining firm 1 and 2’s respective exit periods as ![]() and
and![]() , we are able to formally describes the probability that firm 2 will exit the market.
, we are able to formally describes the probability that firm 2 will exit the market.
Theorem 3: If firm 1 starts out larger than firm 2 in period 0, then the probability that ![]() equals 1. That is, firm 2 always fails before firm 1.
equals 1. That is, firm 2 always fails before firm 1.
Proof: See Appendix.
Although there is still a chance that firm 1 will fail, its probability of failure diminishes with the exit of firm 2. When firm 2 exits the market, Equation (6) shows that firm 1 will grow more rapidly toward its long-run optimum. This increase in size helps insulate firm 1 from failure.
The next question of interest is the precise probability that firm 2 will exit. Is this probability less than 1 [i.e.,![]() ] or will firm 2 exit with certainty as t → ∞ [i.e.,
] or will firm 2 exit with certainty as t → ∞ [i.e.,![]() ]? The following theorem answers this question.
]? The following theorem answers this question.
Theorem 4: Let the difference in starting values be sufficiently small, such that![]() . In this case, the probability of firm 2 exit as t → ∞ is less than 1:
. In this case, the probability of firm 2 exit as t → ∞ is less than 1:![]() .
.
Proof: See Appendix.
In order to gain greater insight into the likelihood of firm 2 failure, we calculate the lower bound on this probability. This model produces the following result.
Theorem 5: The lower bound on the probability of firm 2 exit is![]() . That is,
. That is, ![]() .
.
Proof: See Appendix.
The lower bound is less than 1, and it falls as m and ![]() increase and as
increase and as ![]() decreases. This has a reasonable economic interpretation: firm 2 is likely to have a better chance of survival when it is larger in size, operates in a larger market (i.e., as m increases), and is better able to deal with behavioral errors (i.e., as
decreases. This has a reasonable economic interpretation: firm 2 is likely to have a better chance of survival when it is larger in size, operates in a larger market (i.e., as m increases), and is better able to deal with behavioral errors (i.e., as ![]() diminishes). The prediction that a larger firm is less likely to fail than the smaller firm is consistent with the empirical evidence found in Dunn et al. [10] for a cross section of USA industries and with the evidence of Tremblay and Tremblay [11] for the USA brewing industry.
diminishes). The prediction that a larger firm is less likely to fail than the smaller firm is consistent with the empirical evidence found in Dunn et al. [10] for a cross section of USA industries and with the evidence of Tremblay and Tremblay [11] for the USA brewing industry.
5. Concluding Remarks
In this paper, we have extended the dynamic Cournot model to include behavioral errors on the part of management. The dynamic portion of the model follows the literature by assuming that firms face a cost of adjusting output. Thus, firms do not immediately adjust output to a new equilibrium after a behavioral error is made. Management error in this dynamic setting is modeled with Brownian motion. To our knowledge, we are the first to include Brownian motion in an oligopoly model.
The model produces several interesting results. First, Theorem 2 shows that the limiting output level is a random variable rather than a constant, as is found in the non-stochastic version of the dynamic Cournot model. It also indicates that the limiting variance in firm output is smaller in duopoly than in monopoly. Finally, Theorems 2 - 5 indicate that the probability of firm failure decreases for markets that are larger in size and for firms that are larger and more efficient at dealing with behavioral errors.
Acknowledgements
We would like to thank Roland Eisenhuth, Jenny Lin, Todd Pugatch, Carol Tremblay, Edward Waymire, Patrick De Leenheer and two anonymous referees for helpful comments on an earlier version of the paper.
Appendix
Proof of Theorem 1
We present this system of Equations (6) and (7) in matrix form:
![]() (A1)
(A1)
The eigenvalues of ![]() a
a ![]() and
and ![]() and the corresponding eigenvectors is
and the corresponding eigenvectors is ![]() and
and![]() . It is worthy to note that the eigenvalues are negative. It makes the path of
. It is worthy to note that the eigenvalues are negative. It makes the path of ![]() converges.
converges.
We diagonalize this SDE system using the eigenvectors.
Let![]() ,
, ![]() , and
, and ![]()
Transforming ![]() yields the transformed coordinate of x. We need to transform x to solve SDE.
yields the transformed coordinate of x. We need to transform x to solve SDE.
![]() (A2)
(A2)
![]() (A3)
(A3)
![]() (A4)
(A4)
The solution of this stochastic equations is:
![]() (A5)
(A5)
![]() (A6)
(A6)
where ![]() (or
(or![]() ) is the initial value.
) is the initial value.
From![]() , we recover:
, we recover:
![]() (A7)
(A7)
![]() (A8)
(A8)
where ![]() (or
(or![]() ) is the initial quantity of firm 1 (or 2). Substituting
) is the initial quantity of firm 1 (or 2). Substituting![]() , we have:
, we have:
![]() (A9)
(A9)
![]() (A10)
(A10)
Because of![]() , we can rewrite (A10) into:
, we can rewrite (A10) into:
![]() (A11)
(A11)
QED
Proof of Theorem 2
From (A9) and (A11), the mean is:
![]() (A12)
(A12)
![]() (A13)
(A13)
The variance of (A9) and (A11) is the same as below:
![]() (A14)
(A14)
Since![]() , we reset (A14):
, we reset (A14):
![]() (A16)
(A16)
![]() (A17)
(A17)
Accordingly,
![]() (A18)
(A18)
![]() (A19)
(A19)
QED
Proof of Theorem 3
We multiply both sides of (A9) and (A11) by![]() :
:
![]() (A20)
(A20)
![]() (A21)
(A21)
Let ![]() and
and![]() . Then, hitting time of
. Then, hitting time of ![]() is the same as that of
is the same as that of ![]() and so it suffice to see hitting time of
and so it suffice to see hitting time of![]() . We can rephrase (A20) and (A21):
. We can rephrase (A20) and (A21):
![]() (A22)
(A22)
![]() (A23)
(A23)
We put them in differential form,
![]() (A24)
(A24)
![]() (A25)
(A25)
Since the drifting term of ![]() is larger than
is larger than ![]() but diffusion terms are the same,
but diffusion terms are the same, ![]() , i.e., firm 2 always fails earlier than firm 1. QED
, i.e., firm 2 always fails earlier than firm 1. QED
Proof of Theorem 4
Let ![]() and
and![]() . Then, we reset (A25):
. Then, we reset (A25):
![]() (A26)
(A26)
Since![]() , the drift term
, the drift term ![]() is positive, so
is positive, so![]() .
.
QED
Proof of Theorem 5
We reset (A25):
![]() (A27)
(A27)
We have to find a function ![]() such that
such that ![]() in order to know
in order to know
![]() . It is a challenge and so we seek for a possible exploration of a lower bound for the probability.
. It is a challenge and so we seek for a possible exploration of a lower bound for the probability.
We change the drift of (A27) so that we can find an explicit value of the possibility of ![]() hitting zero. We suggest a new stochastic process with a larger drift term:
hitting zero. We suggest a new stochastic process with a larger drift term:
![]() (A28)
(A28)
Since the new stochastic process has a larger drift term, the possibility of ![]() hitting 0 is less than the possibility of
hitting 0 is less than the possibility of ![]() hitting zero. Therefore, once we find the possibility of
hitting zero. Therefore, once we find the possibility of ![]() hitting 0, it becomes a lower bound for
hitting 0, it becomes a lower bound for![]() . Let
. Let![]() .
.
![]() (A29)
(A29)
Then, ![]() is a martingale process. Let’s put a closed interval set
is a martingale process. Let’s put a closed interval set ![]() for
for![]() . We know
. We know ![]() . Let
. Let ![]() (or
(or![]() ) be a stopping time for
) be a stopping time for ![]() to exit the interval at 0 (or
to exit the interval at 0 (or![]() ). Notice that when
). Notice that when![]() ,
,![]() . By optional stopping theorem (see Grimmett and Stirzaker [12] ),
. By optional stopping theorem (see Grimmett and Stirzaker [12] ),
![]() (A30)
(A30)
![]() (A31)
(A31)
A lower bound for business failure is![]() .
.
QED
NOTES
1A similar conclusion emerges in the Bertrand model when products are differentiated. For a more complete discussion, see Shy [1] (Chapter 6) and Tremblay and Tremblay [2] (Chapter 10).
![]()
2Other examples that use this framework include Fisher [5] , Maskin and Tirole [6] and Dockner [7] .
![]()
3For a detailed discussion of industrial organization models with bounded rationality, see Spiegler [8] and Tremblay and Tremblay [2] .
4Brownian motion is described by a Wiener process. It is related to a stochastic process, much like a standard normal distribution is related to random variables. A normal distribution arises as a limiting distribution for a suitable sequence of random variables, while a Brownian motion arises as a limiting distribution for a suitable sequence of stochastic processes. More specifically, a standard Brownian motion {W(t): t ≥ 0} is a stochastic process that has a continuous path, is stationary, and is independent over time where W(t) ~ N(0, t) "t ≥ 0. Brownian motion has been extensively in the fields of physics, biology, and finance, as discussed by Oksendal [9] .
![]()
5For Orstein-Uhlenbeck mean-reverting equation, ![]() , see Oksendal [9] .
, see Oksendal [9] .
![]()
6This assumption is reasonable if firms are cautious when entering a new market. In any case, the main results of this paper are the same when we assume that firms start out by producing more than their long-run equilibrium level of output.
7This can occur if firm exit tarnishes the reputation of the firm to such an extent that the cost of reentry is prohibitively high.