Remarks on the Complexity of Signed k-Domination on Graphs

Chuan-Min Lee¹, Cheng-Chien Lo¹, Rui-Xin Ye², Xun Xu², Xiao-Han Shi², Jia-Ying Li²

¹Department of Computer and Communication Engineering, Ming Chuan University, The First American University in Asia, Taoyuan, Taiwan, Chinese Taipei.
²Department of Electronic Information Engineering, Fuzhou University, Fuzhou, China.

DOI: 10.4236/jamp.2015.31005                

Abstract

This paper is motivated by the concept of the signed k-domination problem and dedicated to the complexity of the problem on graphs. For any fixed nonnegative integer k, we show that the signed k-domination problem is NP-complete for doubly chordal graphs. For strongly chordal graphs and distance-hereditary graphs, we show that the signed k-domination problem can be solved in polynomial time. We also show that the problem is linear-time solvable for trees, interval graphs, and chordal comparability graphs.

Keywords

Graph Algorithm, Signed k-Domination, Strongly Chordal Graph, Tree, Fixed Parameter Tractable

1. Introduction

Let G = (V, E) be a finite, undirected, simple graph. For any vertex the open neighborhood of v in G is 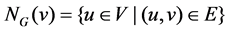and the closed neighborhood of v is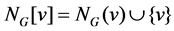. The degree of a vertex v in G is 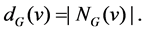We also use V(G) and E(G) to denote vertex set and edge set of G, respectively. If nothing else is stated, it is understood that |V(G)| = n and |E(G)| = m. Let Y be a subset of real numbers. Let 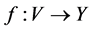be a function which assigns to each 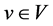a value in Y. Let 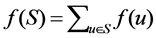for any subset S of V and let f(V) be the weight of f. In 2012, Wang [1] studied the notion of signed k-domination on graphs as follows. Let k be a fixed nonnegative integer and let G = (V, E) be a graph. A signed k-dominating function of G is a function 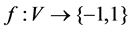such that 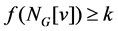for every vertex 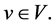The signed k-domination number of G, denoted by 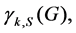is the minimum weight of a signed k-dominating function of G. The signed k-domination problem is to find a signed k-dominating function of G of minimum weight. Clearly, the signed k-domination problem is the signed domination problem if k = 1 [2]. Wang [1] presented several sharp lower bounds of these numbers for general graphs. In this paper, we study the signed k-domination problem for several well-known classes of graphs such as doubly chordal graphs, strongly chordal graphs, distance-hereditary graphs, trees, interval graphs, and chordal comparability graphs.

2. NP-completeness Results

Before presenting the NP-complete results, we restate the signed k-domination problem as decision problems as follows: Given a graph G = (V, E) and a nonnegative integer k and an integer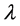, is?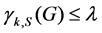

Theorem 1 [3] [4] For any integer k = 0 or 1, the signed k-domination problem on doubly chordal graphs and bipartite planar graphs is NP-complete

Theorem 2. For any fixed integer 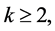the signed k-domination problem on doubly chordal graphs is NP-complete.

Proof. Clearly, the signed k-domination problem on doubly chordal graphs is in NP. By Theorem 1, the signed 0-domination and 1-domination problems on doubly chordal graphs are NP-complete. In the following, we show the NP-completeness of the signed k-domination problem on doubly chordal graphs by a polynomial-time reduction from the signed -domination problem on doubly chordal graphs.

Let be a doubly chordal graph with |V| = n. A clique is a subset of pairwise adjacent vertices in a graph. If a clique consists of j vertices, then it is called a j-clique. We construct a graph H from G by the following steps.

1) We construct a new vertex u and connect u to every vertex of G.

2) We construct 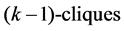and connect the vertex u to every vertex of for

. Note that for

Clearly, the graph H is a doubly chordal graph [5]-[8] and can be constructed in polynomial time. In the following, we show that

Suppose that g is a minimum signed function of G. Then, Let be a function of H defined by for every vertex and for every vertex It can be easily verified that h is a signed k-dominating function of H. We have

Conversely, let and let f be a minimum signed k-dominating function of H. Since is a k-clique, for every vertex and thus By the construction of H, the vertex u is adjacent to every vertex v of G. We know that Then, Let be a function of G defined by for every vertex The function g is a signed function of G. We have

Therefore, Following the discussion above, we know that It implies that for any integer if and only if

3. Polynomial-Time Solvable Results

In this section, we show that the signed k-domination problem is polynomial-time solvable for strongly chordal graphs and distance-hereditary graphs and linear-time solvable for trees, interval graphs, and chordal comparability graphs.

3.1. Strongly Chordal Graphs

Let be a graph. A clique is a subset of pairwise adjacent vertices of A vertex is simplicial if and only if all vertices of form a clique. The ordering of the vertices of is a perfect elimination ordering of G if for all, is a simplicial vertex of the subgraph of G induced by [9]. Let denote the closed neighborhood of in. A perfect elimination ordering is called a strong elimination ordering if it satisfies the following condition:

For if and belong to in, then.

Farer [10] showed that a graph is strongly chordal if and only if it has a strong elimination ordering. Currently, the fastest algorithm to recognize a strongly chordal graph and give a strong elimination ordering takes [11] or time [12]. Strongly chordal graphs include many interesting classes of graphs such as trees, block graphs, interval graphs, and directed path graphs [13]. In the paper [3], Lee and Chang introduced the concept of L-domination. The definition of L-domination is as follows.

Let be fixed integer such that and Let Y be the set Suppose that is a graph. Let L be a labeling function which assigns to each a label where and is a fixed integer. An L-dominating function of a graph is a function satisfying the following two conditions:

1) If then.

2) for every vertex

The L-domination number of G, denoted by is the minimum weight of an L-dominating function of G. The L-domination domination problem is to find an L-dominating function of G of minimum weight. Lee and Chang obtained the following result.

Theorem 4 [3] For any strongly chordal graph G, the L-domination problem can be solved in time if a strong elimination ordering of G is given.

We show a connection between and the signed k-domination problem and a special case of the L-domination problem in Theorem 3.

Theorem 5. Suppose that and Let k be a nonnegative integer and let be a graph in which each is associated with a label. Then, a minimum L-dominating function of G is equivalent to a minimum signed k-dominating function of G.

Proof. Clearly, We assume that is a minimum L-dominating function of G and each is associated with a label Then, and is a signed k-dominating function of G. We have Conversely, we assume that is a minimum signed k-dominating set of G. Then, for every vertex It can be easily verified that g is an L-dominating function of G. We have Following the discussion above, we know that and Hence, and the theorem holds.

Theorem 6. For any nonnegative integer k, the signed k-domination problem on a strongly chordal graph G can be solved in O(n + m) time if a strong elimination ordering of G is given.

Proof. The theorem follows from Theorems 4 and 5.

Theorem 7. For any nonnegative integer k, the signed k-domination problem is linear-time solvable for trees.

Proof. Trees are both chordal and strongly chordal [13]. Let G be a tree. A perfect elimination ordering of the vertices in G can be obtained in linear time [14]. Since G is a tree, has at most one neighbor in for any Otherwise, forms a clique with at least three vertices and it contradicts the assumption that G is a tree. Therefore, the ordering is also a strong elimination ordering of G. Following Theorem 6, we know that the signed k-domination problem is linear-time solvable for trees.

Theorem 8. For any nonnegative integer k, the signed k-domination problem is linear-time solvable for interval graphs.

Proof. An interval graph G is the intersection graph of a set of intervals on a line. That is, each interval corresponds to a vertex of G and two vertices are adjacent if and only if the corresponding intervals intersect. The set of intervals constitutes an interval model of the graph. Booth and Lueker [15] gave the first linear-time algorithm for recognizing interval graphs and constructing interval models for the interval graphs.

Let I be an interval model of an interval graph G. Each interval in the interval model has a right endpoint and a left endpoint. Without loss of generality, we may assume that all endpoints of the intervals in I are pairwise distinct, since, when they are not, it is easy to make this true without altering the represented graph. Let l(v) and r(v) denote the left and right endpoints of the interval corresponding to v. We order the vertices of G by the increasing order of right endpoints of the intervals in I, and let the ordering be v₁,v₂,…,v_n. For any we know that r(v_i) < r(v_j) and l(v_j) < r(v_i) if v_i is adjacent to v_j in G. Therefore, the vertices of N_i[v_i] form a clique and v_i is a simplicial vertex of G_i. The ordering v₁,v₂,…,v_n is a perfect elimination ordering and can be obtained in linear time.

For i < j < k, we assume and belong to N_i[v_i] in G_i. Since v₁,v₂,…,v_n is a perfect elimination ordering, v_j is adjacent to v_k and r(v_j) < r(v_k) and l(v_k) < r(v_i) < r(v_j). Then, every v_p in N_i[v_j] is adjacent to v_k. We have. The ordering v₁,v₂,…,v_n is also a strong elimination ordering of G. By Theorem 6, we know that the signed k-domination problem is linear-time solvable for interval graphs.

Theorem 9. For any nonnegative integer k, the signed k-domination problem is linear-time solvable for chordal comparability graphs.

Proof. Let G = (V, E) be a graph. A vertex v in G is a simple vertex if for any two neighbors x and y of v, either the closed neighborhood of y is a subset of the closed neighborhood of x or the closed neighborhood of x is a subset of the closed neighborhood of y. An ordering v₁,v₂,…,v_n is a simple elimination ordering if for each, the vertex v_i is a simple vertex of the subgraph G_i induced by the vertices v_i,v₂,…,v_n.

A simple elimination ordering of a chordal comparability graph can be obtained in linear time [16]. Sawada and Spinrad [17] presented a linear-time algorithm to transform a simple elimination ordering of a strongly chordal graph to a strong elimination ordering. Therefore, the theorem is true.

3.2. Distance-Hereditary Graphs

The distance between two vertices u and v of a graph G is the number of edges of a shortest path from u to v. If any two distinct vertices have the same distance in every connected induced subgraph containing them, then G is a distance-hereditary graph. In 1997, Chang, Hsieh, and Chen [18] showed that distance-hereditary graphs can be defined recursively.

Theorem 10 [18] Distance-hereditary graphs can be defined as follows.

1) A graph consisting of only one vertex is distance-hereditary, and the twin set is the vertex itself.

2) If and are disjoint distance-hereditary graphs with the twin sets and, respectively, then the graph is a distance-hereditary graph and the twin set of is G is said to be obtained from and by a false twin operation.

3) If and are disjoint distance-hereditary graphs with the twin sets and, respectively, then the graph obtained by connecting every vertex of to all vertices of is a distance-hereditary graph and the twin set of is G is said to be obtained from and by a true twin operation.

4) If and are disjoint distance-hereditary graphs with the twin sets and, respectively, then the graph obtained by connecting every vertex of to all vertices of is a distance-hereditary graph and the twin set of is G is said to be obtained from and by a pendant vertex operation.

Following Theorem 10, a distance-hereditary graph G can be represented as a binary ordered decomposition tree and the decomposition tree can be obtained in linear-time [18]. In this decomposition tree, each leaf is a single vertex graph, and each internal node represents one of the three operations: pendant vertex operation (labeled by P), true twin operation (labeled by T), and false twin operation (labeled by F). Therefore, the decomposition tree is called a PTF-tree.

Definition 1. Suppose that is a distance-hereditary graph. Let be the twin set of Let a and b be integers such that and A (t, a, b)-function of G is a function satisfying the following three conditions.

1)

2) The function assigns the value 1 to a vertices in TS(G) and the value to b vertices in TS(G).

3) For a vertex if Otherwise,

We define If there does not exist a (t, a, b)- function of G, then It is clear that

We give the following lemmas to compute for a distance-hereditary graph G. The correctness of Lemmas 2 - 5 can be proved by the arguments similar to those for proving Lemmas 1 - 4 in Section III. B of the paper [4].

Lemma 2. Suppose that is a graph of only one vertex v. Then,

Lemma 3. Suppose that is formed from two disjoint distance-hereditary graphs and by a false twin operation. Then,

,

where and

Lemma 4. Suppose that is formed from two disjoint distance-hereditary graphs and by a true twin operation. Then,

,

where and

Lemma 5. Suppose that is formed from two disjoint distance-hereditary graphs and by a pendant vertex operation. Then,

,

where

Theorem 11. For any nonnegative integer k, the signed k-domination problem can be solved in polynomial time for distance-hereditary graphs.

Proof. Following Lemmas 2 - 5 and the recursive definition of distance-hereditary graphs in Theorem 10, we can design a dynamic programming algorithm to compute the signed k-domination number of a distance-here- ditary graph G in polynomial time. Moreover, it is not difficult to see that a minimum signed k-dominating function of a distance-hereditary graph G can be obtained in polynomial time, too.

Acknowledgements

This research was partially supported under Research Grants: NSC-102-2221-E-130-004 and MOST-103-2221- E-130-009 in Taiwan.

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Wang, C. (2012) The Signed k-Domination Numbers in Graphs. Ars Combinatoria, 106, 205-211.
[2]	Hattingh, J.H., Henning, M.A. and Slater, P.J. (1995) The Algorithmic Complexity of Signed Domination in Graphs. Australasian Journal of Combinatorics, 12, 101-112.
[3]	Lee, C.-M. and Chang, M.-S. (2008) Variations of Y-Dominating Functions on Graphs. Discrete Mathematics, 308, 4185-4204. http://dx.doi.org/10.1016/j.disc.2007.08.080
[4]	Lee, C.-M. (2014) Remarks on the Complexity of Non-negative Signed Domination. Journal of Networks, 9, 2051- 2058. http://dx.doi.org/10.4304/jnw.9.8.2051-2058
[5]	Brandst?dt, A., Dragan, F.F., Chepoi, V.D. and Voloshin, V. (1998) Dually Chordal Graphs. SIAM Journal on Discrete Mathematics, 11, 437-455. http://dx.doi.org/10.1137/S0895480193253415
[6]	Cai, L., Chen, J., Downey, R.G. and Fellows, M.R. (1997) Advice Classes of Parameterized Tractability. Annals of Pure and Applied Logic, 84, 119-138. http://dx.doi.org/10.1016/S0168-0072(95)00020-8
[7]	Downey, R.G. and Fellows, M.R. (1999) Parameterized Complexity. Monographs in Computer Science, Springer- Verlag.
[8]	Moscarini, M. (1993) Doubly Chordal Graphs, Steiner Trees, and Connected Domination. Networks, 23, 59-69. http://dx.doi.org/10.1002/net.3230230108
[9]	Rose, D.J. (1970) Triangulated Graphs and the Elimination Process. Journal of Mathematical Analysis and Applications, 32, 597-609. http://dx.doi.org/10.1016/0022-247X(70)90282-9
[10]	Farber, M. (1983) Characterizations of Strongly Chordal Graphs. Discrete Mathematics, 43, 173-189. http://dx.doi.org/10.1016/0012-365X(83)90154-1
[11]	Paige, R. and Tarjan, R.E. (1987) Three Partition Refinement Algorithms. SIAM Journal on Computing, 16, 973-989. http://dx.doi.org/10.1137/0216062
[12]	Spinrad, J.P. (1993) Doubly Lexical Ordering of Dense 0-1 Matrices. Information Processing Letters, 45, 229-235. http://dx.doi.org/10.1016/0020-0190(93)90209-R
[13]	Brandst?dt, A., Le, V.B. and Spinrad, J.P. (1999) Graph Classes: A Survey. SIAM Monographs on Discrete Mathematics and Applications, Philadelphia 1999. http://dx.doi.org/10.1137/1.9780898719796
[14]	Tarjan, R.E. and Yannakakis, M. (1984) Simple Linear Algorithms to Test Chordality of Graphs, Test Acyclicity of Hypergraphs, and Selectively Reduce Acyclic Hypergraphs. SIAM Joural on Computing, 13, 566-579. http://dx.doi.org/10.1137/0213035
[15]	Booth, S. and Lueker, S. (1976) Testing for the Consecutive Ones Property, Interval Graphs, Graph Planarity Using PQ-Trees Algorithms. Journal of Computer and System Sciences, 13, 335-379. http://dx.doi.org/10.1016/S0022-0000(76)80045-1
[16]	Borie, R.B. and Spinrad, J.P. (1999) Construction of a Simple Elimination Scheme for a Chordal Comparability Graph in Linear Time. Discrete Applied Mathematics, 91, 287-292. http://dx.doi.org/10.1016/S0166-218X(98)00137-1
[17]	Sawada, J. and Spinrad, J.P. (2003) From a Simple Elimination Ordering to a Strong Elimination Ordering in Linear Time. Information Processing Letters, 86, 299-302. http://dx.doi.org/10.1016/S0020-0190(03)00228-X
[18]	Chang, M.-S., Hsieh, S.-Y. and Chen, G.-H. (1997) Dynamic Programming on Distance-Hereditary Graphs. Proceedings of the 8th International Symposium o Algorithms and Computation, Lecture Notes in Computer Science, Vol. 1350, 344-353.