Irreducible Representations of Algebraic Group SL(6,K) in charK =3

Zhongguo Zhou^*

College of Science, Hohai University, Nanjing, China.

DOI: 10.4236/apm.2014.410062                

Abstract

For each irreducible module Xi Nanhua defined an element which generated this module. We use this element to construct a certain basis for and then compute dim , determine its formal characters in this paper. In order to obtain faster speed we modify the algorithm to compute the irreducible characters.

Keywords

Irreducible Character, Semisimple Algebraic Group, Composition Factor

1. Introduction

The determination of all irreducible characters is a big theme in the modular representations of algebraic groups and related finite groups of Lie type. But so far only a little is known concerning it in the case when the characteristic of the base field is less than the Coxeter number.

Gilkey-Seitz gave an algorithm to compute part of characters of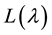’s with 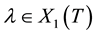for 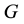being of type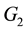, , 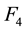, 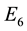and 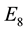in characteristic 2 and even in larger primes in [1] . Dowd and Sin gave all characters of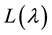’s with 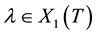for all groups of rank less than or equal to 4 in characteristic 2 in [2] . They got their results by using the standard Gilkey-Seitz algorithm and computer. L. Scott et al. computes the characters for 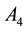when, by computing the maximal submodule in a baby Verma module [3] . Anders Buch and Niels Lauritzen also obtain this result for when with Jantzen’s sum formula [4] .

An element for each irreducible module with was defined in [[5] ,

39.1, p. 304] and [[6] , p. 239]. This element could be used in constructing a certain basis for, computing, and determining. In this way, Xu and Ye, Ye and Zhou determined all irreducible characters for the special linear groups, and, the special orthogonal group and the symplectic group over an algebraically closed field of characteristic 2 in [7] [8] and for the special orthogonal group and the symplectic group over an algebraically closed field of characteristic 3 in [9] [10] . However, it needs so much time to compute the irreducible characters for other groups. In the present note, we shall work out all irreducible characters for the simple algebraic groups of type over an algebraically closed field of characteristic 3 with modified algorithm to obtain faster speed. We shall freely use the notations in [9] [11] without further comments.

2. Preliminaries

Let be the simple algebraic group of type over an algebraically closed field of characteristic 3. Take a Borel subgroup and a maximal torus of with. Let be the character group of, which is also called the weight lattice of with respect to. Let be the root system associated to, and choose a positive root system in such a way that corresponds to. Let

be the set of simple roots of such that

Let be the fundamental weights of such that, the Kronecker delta, and denote by the weight with, the integer ring. Then the dominant weight set is as follows:

Let be the Weyl group and let be the affine Weyl group of. It is well-known that for, is the induced -module from the 1-dimensional -module which contains a unique irreducible -submodule of the highest weight. In this way, parameterizes the finite-dimensional irreducible -modules. We set and for all. Moreover, is given by the Weyl character formula, and for, we have

For, we have

Let be the -th Frobenius morphism of with the scheme-theoretic kernel of. Let be the Frobenius twist for any -module. It is well-known that is trivial regarding as a - module. Moreover, any -module has such a form if the action of on is trivial. Let

Then the irreducible -modules’s with remain irreducible regarded as the -modules. On the other hand, any irreducible -module is isomorphic to exactly one of them.

For, we have the unique decomposition

Then the Steinberg tensor product theorem tells us that

Therefore we can determine all the characters with by using the Steinberg tensor product theorem, provided that all the characters with are known.

Recall the strong linkage principle in [12] . We define a strong linkage relation in if occurs as a composition factor in. Then is irreducible when is a minimal weight in with respect to the partial ordering determined by the strong linkage relations.

Let be the simple Lie algebra over which has the same type as, and the universal enveloping algebra of. Let, be a Chevalley basis of. We also denote by, respectively, where The Kostant -form of is the -subalgebra of generated by the elements, for and. Set

Then for, ,. Define and call the hyperal-

gebra over associated to. Let be the positive part, negative part, zero part of, respec-

tively. They are generated by, and, respectively. By abuse of notations, the images in of

, , , etc. will be denoted by the same notations, respectively. The algebra is a Hopf alge-

bra, and has a triangular decomposition. Given a positive integer, let be the sub-

algebra of generated by the elements, , for, and. In

particular, is precisely the restricted enveloping algebra of. Denote by the positive part, negative part, zero part of, respectively. Then we have also a triangular decomposition. Given an ordering in, it is known that the PBW-type bases for resp. for have the form of

with resp. with.

Let. We set for, here each element is also viewed as a certain set of simple roots. Following [5] [6] , we define an elements in by

As a special case of [[5] , Theorems 6.5 and 6.7], we have

Theorem 1 Assume that is a simple Lie algebra of the simple algebraic group of type over an algebraically closed field of characteristic 3. Let.

(i) The element lies in.

(ii) Let be the left ideal of generated by the elements

and the elements with. Then (Note that has a -module structure, which is irreducible).

(iii) As a -module, is isomorphic to.

By abuse of notations, the images in of and will be denoted by the same notations. We shall use this theorem to computer the multiplicities of the weight spaces for all the dominant weight of, to compute, and to determine in this note, when is the simple algebraic group of type.

3. Characters of Irreducible Modules of

From now on we shall assume that. Denote by the dual module of, then we have by the duality that, and. Furthermore, the elements satisfy the following commutator relations:

Now we can obtain our main theorems. Let be the sum of weights of the W-orbit of

for all. It is well-known that, and

form bases of, the W-invariant subring of, respectively. According to the Weyl character formula and the Freudenthal multiplicity formula, we get a change of basis matrix from to, which is a triangular matrix with 1 on its diagonal, i.e.

with (cf. [10] ). Based on our computation, we get another change of basis matrix

from to, which is also a triangular matrix with 1 on its diagonal.

Let us mention our computation of more detailed. First of all, we compute for any. It is well known that for each dominant weight of, can be expressed in terms of sum of positive roots, and there exist many ways to do so. Each way corresponds to an element in. Then we compute various. Note that each can be written as a linear combination of the basis elements of with non-negative integer coefficients, and the typical images of all non-zero’s generate the weight space of the irreducible submodule of. Therefore, we can easily determine the dimension of, provided that we compute the rank of the set of all these non-zero’s. It can be reduced to compute the rank of a corresponding matrix. Finally, we obtain the formal character of, which can be written as a linear combination of’s with non-negative integer coefficients. That is

with. In this way, we get the second matrix.

For example, we assume that is the simple algebraic group of type and.

It is easy to see that

For, we have First we compute each of the set . Then we compute the rank of the set, which is equal to 2. So we have

. For, we have We compute each of the set

and then we compute the rank of the set, which is equal to 13. So we have. By this methods, we can calculate all multiplicity Finally, we obtain the formal character of irreducible module

When lies in but not in, we can also compute the formal character by using the Steinberg tensor product theorem. For, we have the unique decomposition

Then the Steinberg tensor product theorem tells us that

Therefore, we can determine all characters with, provided that all characters with are known. For example, when, we have

Therefore, from the two matrices, we can easily get the third change of basis matrix from to, which is still a triangular matrix with 1 on its diagonal. The matrix gives the decomposition patterns of various with.

We list the matrix in the attached tables. In all these tables, the left column indicates’s. For two weight, the number in tables is just the multiplicity of composition factors .

4. Faster Algorithm

In paper [9] [10] , we compute the multiplicity one by one for a fixed weight However, noticing that some information computing may be useful to compute for So we compute all possible such that spanning to the whole firstly. Then we compute in some ordering: if then we first obtain save this result and compute instead of computing directly. In fact we only need compute for some positive root and in one step.

For example, suppose to compute we can compute at the first step, and then compute In this way, we can avoid much repeated work.

In order to obtain the results the computer must work several days. So we must be careful to avoid error. There are facts to verity the results.

At firstly, we compute the dimension of weight space, then by Sternberg tensor formula and Weyl formula we obtain the decomposition pattern of At last checking all the data we find that

1). Symmetry of dimension of weight space. Checking the results the two equations are satisfied:

2). Symmetry of composition factors. From the decomposition patterns, the following equations are hold:

3). Positivity of multiplicity of composition factors. All the multiplicity of composition factors we obtained are nonnegative.

4). Linkage principle is hold. If the multiplicity of composition factors then we have

From the representation theory of algebraic groups, all the above results should be hold, so the computational data is compatible with the theory.

5. Main Results

Theorem 2 When, let

Then is an irreducible -module for all and the decomposition patterns of for all are listed in Tables 1-8.

Remark: The table should be read as following. We list the weights in the first collum and write the multiplicity of composition factors as the others elements of tables. For example, from the third row in Table 1, we obtain 00200 0 1 1, this mean

Table 1. The linkage class (00000).

Table 2. The linkage class (00001), (10002).

Table 3. The linkage class (10210), (21021), (02102), (22010), (10010).

Table 4. The linkage class (10012), (10100).

Table 5. The linkage class (12010), (02101), (01012), (20101), (20002).

Table 6. The linkage class (00002), (00010).

Table 7. The linkage class (00100).

Table 8. The linkage class (00122), (01010), (10101), (00022).

According to the symmetry of we need not list all results. For example, we can obtain the decomposition pattern of from Table 2:

So we also have

Acknowledgements

We thank the Editor and the referee for their comments. This work was supported by the Natural Science Fund of Hohai University (2084/409277,2084/407188) and the Fundamental Research Funds for the Central Universities 2009B26914 and 2010B09714. The authors wishes to thank Prof. Ye Jiachen for his helpful advice.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Gilkey, P.B. and Seitz, G.M. (1988) Some Representations of Exceptional Lie Algebras. Geometriae Dedicata, 25, 407-416. http://dx.doi.org/10.1007/BF00191935
[2]	Dowd, M. and Sin, P. (1996) On Representations of Algebraic Groups in Characteristic Two. Communications in Algebra, 24, 2597-2686. http://dx.doi.org/10.1007/BF00191935
[3]	http://pi.math.virginia.edu/~lls2l/research_undergrad.htm
[4]	http://math.rutgers.edu/~asbuch/dynkin/
[5]	Lusztig, G. (1993) Introduction to Quantum Groups. Progress in Mathematics, 110, Birkháuser.
[6]	Xi, N.H. (1996) Irreducible Modules of Quantized Enveloping Algebras at Roots of 1. Publ. RIMS, Kyoto Univ, 32, 235-276. http://dx.doi.org/10.2977/prims/1195162964
[7]	Xu, B.X. and Ye, J.C. (1997) Irreducible Characters of Algebraic Groups in Characteristic Two (I). Algebra Colloquium, 4, 281-290.
[8]	Ye, J.C. and Zhou, Z.G. (2000) Irreducible Characters of Algebraic Groups in Characteristic Two (III). Communications in Algebra, 28, 4227-4247. http://dx.doi.org/10.1080/00927870008827086
[9]	Ye, J.C. and Zhou, Z.G. (2001) Irreducible Characters for Algebraic Groups in Characteristic Three. Communications in Algebra, 29, 201-223. http://dx.doi.org/10.1081/AGB-100000795
[10]	Ye, J.C. and Zhou, Z.G. (2002) Irreducible Characters for Algebraic Groups in characteristic Three (II). Communications in Algebra, 30, 273-306. http://dx.doi.org/10.1081/AGB-120006491
[11]	Jantzen, J.C. (1987) Representations of Algebraic Groups. Academic Press, Orlando.
[12]	Andersen, H.H. (1980) The Strong Linkage Principle. Journal fur die Reine und Angewandte Mathematik, 315, 53-59.