Measurement of Thermophysical Property of Energy Storage System (CaCl2.NH3 System) ()
1. Introduction
These days, the possibility of significant global warming resulting from emissions of greenhouse gases by fossil fuel combustion has become an important concern within the international community. In order to save energy and utilize the renewable energy as natural resources, The thermal energy storage systems utilizing the low temperature heat sources such as solar energy (approx. 353 - 373 K) have been proposed and developed, the processes using the chemical reaction of an anhydrous salt with NH3 have been proposed and discussed for their practicability [1] -[7] . For example, some prototypes of thermal energy storage unit using CaCl2・mNH3 system (see the following chemical reaction: ammoniation and deammoniation) have been designed and these performances [3] -[7] were measured, and because this chemical reaction is well known as higher energy density system as compared with those reactions for other energy storage systems [1] and NH3 is presently attracting an attention as a promising working fluid and NH3 has no relation to greenhouse effect on the earth. Furthermore, recent works of hydrogen (H2) storage systems as one of energy storage systems and/or fuel (H2) carriers of fuel cells (FCs) focused on ammoniated salts [8] -[10] . However, the thermophysical properties (e.g. thermal conductivity, thermal diffusivity) of ammoniated salts on the design of those storage systems have been few experimental studies.
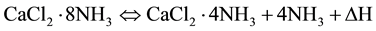
In order to develop the energy storage system and H2 storage system utilizing the above chemical reaction, the measurement unit was developed, and the thermophysical properties (effective thermal conductivity and effective thermal diffusivity) of CaCl2・mNH3 (m = 4, 8) and CaCl2・mNH3with heat transfer media (Ti: titanium) as the important design factors were measured in this study.
Regarding the measurement principle and method, the “any heating method” developed by Iida et al. [11] - [13] was applied to measure the thermophysical properties in this study, and this method could measure effective thermal conductivity and effective thermal diffusivity at the same time during the measuring time.
2. Measurement Principle
2.1. Fundamental Relation of Heat Conduction for One-Dimensional Cylindrical Coordinate
In this study, the thermophysical properties of CaCl2・mNH3 system were measured by the any heating method developed by Iida et al. [11] -[13] . Theme measurement principle is shown below. It is assumed that the heat flow is the direction of radius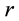 
mm only for the heat conduction on one-dimensional cylindrical coordinate and the initial temperature distribution 
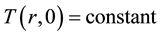(i.e. initial temperature distribution is uniform). The temperature difference on the cylindrical coordinate 
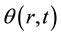K is defined as
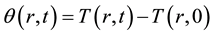(1)
where 
s and 
K are time and temperature, respectively.
The fundamental heat conduction equation can be expressed as
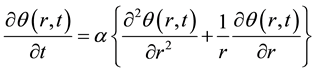(2)
where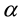 
m2/s is thermal diffusivity.
Taking
Laplace
transform of Equation (2) and substituting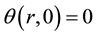 
into Equation (2), and then Equation (2) is rewritten to the ordinary differential equation, and the general solution is given by
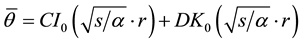(3)
where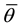 
and 
are
Laplace
integration of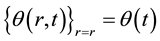 
and
Laplace
parameter,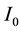 
and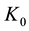 
are ze-
ro order modified
Bessel
functions of the first and the second kinds and ![]()
and ![]()
are constants of integration, respectively.
On the other hand, the heat flux ![]()
W/m2 is given by
Fourier
’s equation.
![]()
(4)
where ![]()
W/(m・K) is thermal conductivity.
Taking
Laplace
transform of Equation (4) and substituting Equation (4) into Equation (4), then Equation (5) is given as
![]()
(5)
2.2. Measurement System
Figure 1 shows the principle of measurement system by the any heating method. This measurement system consists of the hollow cylindrical sample [I] and the cylindrical sample [II]. The symbol × is a measurement point of temperature and the measurement point 2 is expressed as the boundary surface. It is assumed that the direction of radius r (mm) only and the contact resistance is negligible. The temperature response ![]()
at each measurement point i (i = 0, 1, 2, 3, 4) is rewritten as![]()
,
Laplace
integration of each point can be expressed as
![]()
(6)
In this study, the hollow cylindrical sample [I] is the reference specimen and the cylindrical sample [II] is the measured specimen, and measurement point 4 is unnecessary in this case. In the measured specimen [II],![]()
. Hence![]()
. Thus ![]()
in Equation (5), Equation (3) can be rewritten as
![]()
(7)
where ![]()
is thermal diffusivity of the measured specimen [II].
By measuring ![]()
and ![]()
and ![]()
and ![]()
can be obtained by Equation (6), and substituting ![]()
and ![]()
into Equation (7) and ![]()
is defined as Equation (8), and then Equation (9) can be obtained.
![]()
(8)
![]()
(9)
Therefore, ![]()
which is unknown can be obtained.
The
Laplace
integration of heat flux at ![]()
in the measured specimen [II] by ![]()
and Equation (8) is given by
![]()
(10)
where ![]()
is thermal conductivity of the measured specimen [II].
On the other hand, in the reference specimen [I], by measuring ![]()
and ![]()
and ![]()
and ![]()
are obtained by Equation (6), and substituting ![]()
and ![]()
into Equation (3), then ![]()
and ![]()
can be obtained by
![]()
(11)
![]()
(12)
where ![]()
is the thermal diffusivity of the reference specimen [I], and the thermophysical properties (thermal diffusivity and thermal conductivity) of the reference specimen are well known [14] .
Therefore, the
Laplace
integration of heat flux at ![]()
in the reference specimen [I] can be obtained by![]()
, ![]()
and Equation (5),
![]()
(13)
Since it is clear that![]()
, Equation (14) is derived, and then ![]()
can be obtained.
![]()
(14)
where ![]()
is the thermal conductivity of the reference specimen [I].
Figure 2 shows the measurement system in this study. In this measurement system, the measured specimen [II] is heated from the outside of the reference specimen [I], the temperature responses of central point (i = 0) in the measured specimen and 2 points (i = 2, R) on the reference specimen are measured at the same time in Figure 1. Regarding thermal diffusivity of the measured specimen![]()
, in Equation (9), ![]()
is rewritten as ![]()
and substituting ![]()
into Equation (5), then Equation (15) given as
![]()
(15)
Hence, in this case, ![]()
by Equation (15) is given, thermal diffusivity of the measured specimen ![]()
can be obtained by Figure 3 (the relation between ![]()
and![]()
).
Regarding thermal conductivity of the measured specimen![]()
, in Equation (14), Equation (11) and Equation (12), ![]()
, ![]()
, ![]()
and ![]()
are rewritten as 0, ![]()
, ![]()
and![]()
, then![]()
, ![]()
and ![]()
can be obtained by
![]()
(16)
![]()
(17)
![]()
(18)
3. Experimental Section
3.1. Materials
CaCl2 used in this experiment is produced by Wako Pure Chemicals Industries, Ltd. It is guaranteed reagent
grade, and it is specified as the pure grade having minimum purity of 95.0% and used without further purification. The powdered crystal of CaCl2 is dried at 773 K and is stored over silica gel in a desiccator. NH3 gas of 99.99% purity is provided from Sumitomo Seika Co. Ltd. Titanium sponge (Ti) of 10 - 28 JIS mesh 90% up is provided from Wako Pure Chemical Industries, Ltd., and it is used as the heat transfer media and has minimum purity of 99.0%.
3.2. Experimental Apparatus
Figure 4 schematically shows the experimental apparatus of the measurement system in this experiment. This system consists of stainless steel measurement cell as reactor, NH3 glass vessel, pressure regulator valve, pressure gauges, thermocouples and constant temperature water baths. This measurement cell is covered with the water jacket, and the temperature of this cell can be controlled. The NH3 vessel is pressure resistant glass vessel, whose volume is 0.3 × 10−
3 m 3
(up to 2.0 MPa), and the volume of liquidNH3 is measured by the microscope with an accuracy of ±0.05% of full volume (0.5 × 10−
3 m 3
).
In order to insulate this measurement cell from the surroundings, the apparatus is wrapped by the foamed polystyrol. The each temperature of this apparatus is measured by using C-A (Chromel-Alumel) thermocouples corrected by the digital thermometer, and the temperature data as the digital signal (change of mV) is transferred to the microcomputer and stored. The amount of liquid NH3 transferred to the measurement cell from NH3 vessel can be measured by the microscope. The temperatures of this cell and NH3 vessel are controlled by using the constant temperature water bath throughout the reaction, and the accuracy of temperature control is minimum accuracy within ±0.1 K. The each pressure in these vessels is measured by Bourdon gauge, whose accuracy is ±0.1% of full scale (up to 2.0 MPa). The pressure control in this cell is carried out using the pressure regulator valve.
Figure 5 shows the measurement cell in detail. This measurement cell consists of stainless steel pipe (Length:
230 mm
, OD:
76.3 mm
, ID:
68.3 mm
) as the reactor, reinforced pressure proof glass tube (Pyrex 7740: OD:
40.0 mm
, ID:
32.0 mm
[14] ) as the reference specimen and stainless steel pipe (OD:
0.51 mm
, ID:
0.26 mm
) for thermocouple. The temperature response is measured by the stainless steel sheathed C-A thermocouple (OD:
0.25 mm
), which is inserted into the stainless steel pipe for thermocouple.
The temperature of this measurement cell is increased and controlled by Ni-Cr wire heater and thermistor type temperature controller, and the accuracy of temperature control is minimum accuracy within ±0.1 K. In order to escape non-uniform temperature field and to decrease the thermal resistance, Al2O3 powder is packed between the stainless steel pipe and the reference specimen.
![]()
Figure 4. Experimental apparatus of measurement unit.
3.3. Experimental Procedure
CaCl2 of 1.31 mole (approx.
145 g
) is crushed below size of 200 JIS mesh and was dried at 773 K for 3 hours by an oven. A dried CaCl2 as measured specimen is placed in this measurement cell. It is sealed, and the thermophysical properties (effective thermal conductivity and effective thermal diffusivity) are measured at atmospheric pressure (0.1 MPa) by the same measurement method for ammoniated salts (see
3.3.2
).
Similarly, CaCl2 of 0.218 mole (approx.
24.2 g
) is crushed below size of 200 JIS mesh and was dried at 773 K for 3 hours by an oven. A dried CaCl2 as measured specimen (or a specimen mixed with weighed Ti: weight ratio; Ti/CaCl2 = n, where n = 3) is placed in this cell. It is sealed, worked by the vacuum pump in order to remove an air and any water from this system. NH3 vessel is also evacuated for 2 hours and NH3 gas is introduced from the NH3 gas bomb into NH3 vessel, which is kept at a constant temperature (273 K) by the cooling liquid. After liquid NH3 is charged in it, its volume is measured by the microscope rapidly and recorded. Then this cell is connected with NH3 vessel shown in Figure 4. NH3 gas from NH3 vessel is moved to the cell through the pressure regulator valve keeping the constant pressure (0.5 MPa) during the reaction. The level of liquid NH
3 in
the glass vessel is measured by reading the scale of NH3 vessel using the microscope, and the mole number of NH3 absorbed to the dried CaCl2 is calculated from this volume change of liquid NH
3 in
NH3 vessel. The temperature distribution in this cell is measured using thermocouples at the some points of horizontal axis. The each reaction process in detail is as follows.
3.3.1
. Ammoniation and Deammoniation (CaCl2(+Ti) ⇒ CaCl2・8NH3(+Ti) ⇔ CaCl2・4NH3(+Ti))
When the temperatures of the cell and NH3 vessel are stabilized, a needle valve is opened to keep the constant pressure using the pressure regulator valve in this cell. Operating temperature and pressure in this cell are controlled to 303 K and 0.5 MPa, respectively. The amount of liquid NH3 transferred to the cell from NH3 vessel is measured by reading the scale of NH3 vessel using the microscope. The NH3 mole number absorbed to CaCl2 is calculated from the volume change of liquid NH
3 in
NH3 vessel. When 8 moles of NH3 is absorbed to the pureCaCl2, the experiment of ammoniation is just finished.
The deammoniation from an ammoniated salt (CaCl2・8NH3(+Ti)) is carried out by using the same experimental apparatus. In this case, the NH3 vessel is kept at constant temperature of 293 K by the circulating water from the constant temperature water bath, and the temperatures on horizontal axis in the cell are heated to 353 K by the heating water. The NH3 mole number desorbed from ammoniated salt is calculated by the same method of ammoniation. When 4 moles of NH3 is desorbed from CaCl2・8NH3(+Ti), this deammoniation process is finished. In order to measure the thermophysical properties on repeated runs (ammoniation and deammoniation), the thermophysical properties are measured after the repeated runs (≥10 times each).
3 .3 .2
. Measurement of Thermophysical Properties (CaCl2・4NH3(+Ti) and CaCl2・8NH3(+Ti))
When the measurement temperature and the temperature of measuring points are stabilized in each ammoniated salt (CaCl2・4NH3(+Ti) and CaCl2・8NH3(+Ti)) under the equilibrium pressure, the heating of the measurement cell by charging electricity to the heater is started, and the heating rate and maximum heating temperature are 5 K/min and 10 K/min, respectively. The temperature response as the change of mV by thermocouple of each measuring point is measured, and the scan rate of temperature response is every 9 seconds and the measurement time is 30 minutes. The data of temperature response is corrected by the digital thermometer and the temperature data is transferred to the microcomputer and stored. The thermophysical properties (effective thermal conductivity and effective thermal diffusivity) are calculated from the stored data based on the preceding measurement principle.
4. Results and Discussion
Figure 6 shows the relation between thermophysical properties (effective thermal conductivity ![]()
and effective thermal diffusivity![]()
) of CaCl2 powder alone and temperature. The measured thermophysical properties (![]()
and![]()
) were approximately 0.18 - 0.20 W/(m・K) and 0.31 - 0.33 × 10−
6 m2
/s in the measuring temperature range of 285 - 350 K, respectively. Wang et al. [15] and Fujioka et al. [16] reported the values of ![]()
were approximately 0.110 - 0.145 W/(m・K) at 0.1 MPa (300 - 390 K) and 0.15 W/(m・K) at 0.1 MPa (283 or 293 K) for CaCl2 powder alone, respectively. It seems that the difference in ![]()
comes from the difference of the bulk density (ρbulk) or the void fraction of the specimen in the measurement cell.
Figure 7 shows the relation between ![]()
and ![]()
of CaCl2・4NH3 and temperature. The measured thermophys-
![]()
Figure 6. Relation between thermophysical property of CaCl2 powder alone and temperature.
![]()
Figure 7. Relation between thermophysical property of CaCl2∙4NH3 and temperature.
ical properties (![]()
and![]()
) were approximately 0.06 - 0.08 W/(m・K) and 0.16 - 0.19 × 10−
6 m2
/s in the measuring temperature range of 290 - 350 K, respectively. The value of ![]()
of CaCl2・4NH3 is reduced to approximately 40% of that of CaCl2 powder alone. This is due to the difference of ρbulk of the specimen in the measurement cell (CaCl2・4NH3: ρbulk =
232 kg
/m3, CaCl2 powder alone: ρbulk =
860 kg
/m3). According to Fujioka et al. [16] , it was reported that the value of ![]()
was approximately 0.05W/(m・K) for CaCl2・4NH3 at the equilibrium pressure (283 or 293 K). It seems that the value of ![]()
in this measurement is close to the value of ![]()
in Fujioka et al. [16] .
Figure 8 shows the relation between ![]()
and ![]()
of CaCl2・8NH3 and temperature. The measured thermophysical properties (![]()
and![]()
) were approximately 0.08 - 0.11 W/(m・K) and 0.11 - 0.14 × 10−
6 m2
/s in the measuring temperature range of 290 - 350 K, respectively. Fujioka et al. [16] reported the value of ![]()
was approximately 0.06 W/(m・K) for CaCl2・8NH3 at the equilibrium pressure (283 or 293 K). Similar to the value of ![]()
for CaCl2・4NH3, it seems that the value of ![]()
in this measurement is close to the value of ![]()
in Fujioka et al. [16] . Regarding ![]()
of CaCl2・4NH3 and CaCl2・8NH3, it is found that the value of ![]()
of CaCl2・8NH3 is reduced to approximately 70% of that of CaCl2・4NH3. It seems that this decrease in ![]()
comes from the increase of bulk density and specific heat of the specimen in the measurement cell.
Figure 9 shows the relation between ![]()
and ![]()
of CaCl2・4NH3 + Ti (n = 3) and temperature. The measured thermophysical properties (![]()
and![]()
) were approximately 0.14 - 0.17 W/(m・K) and 0.22 - 0.24 × 10−
6 m2
/s in the measuring temperature range of 290 - 350 K, respectively. In comparing ![]()
of CaCl2・4NH3 + Ti and CaCl2・4NH3, the value of ![]()
of CaCl2・4NH3 + Ti is approximately 2.2 times larger than that of CaCl2・4NH3. Regarding ![]()
of CaCl2・4NH3 + Ti and CaCl2・4NH3, the value of ![]()
of CaCl2・4NH3 + Ti is approximately 1.3 times larger than that of CaCl2・4NH3. It seems that the main cause for the increase of ![]()
is the decrease of the specific heat by the addition of Ti.
Figure 10 shows the relation between ![]()
and ![]()
of CaCl2・8NH3 + Ti and temperature. The measured thermophysical properties (![]()
and![]()
) were approximately 0.17 - 0.20 W/(m・K) and 0.18 - 0.19 × 10−
6 m2
/s in the measuring temperature range of 290 - 350 K, respectively. In comparing ![]()
of CaCl2・8NH3 + Ti and CaCl2・8NH3, the value of ![]()
of CaCl2・8NH3 + Ti is approximately 1.5 times larger than that of CaCl2・4NH3. Regarding ![]()
of CaCl2・8NH3 + Ti and CaCl2・8NH3, the value of ![]()
of CaCl2・8NH3 + Ti is approximately 1.5 times larger than that of CaCl2・8NH3. The relation of obtained values of thermal conductivities for Ti weight ratio (n = 0 and n = 3) in this measurement is similar to that of values of heat flow rates (kJ/h) for Ti weight ratio in
![]()
Figure 8. Relation between thermophysical property of CaCl2∙8NH3 and temperature.
![]()
Figure 9. Relation between thermophysical property of CaCl2∙4NH3 + Ti and temperature.
![]()
Figure 10. Relation between thermophysical property of CaCl2∙8NH3 + Ti and temperature.
authors’ previous work [7] .
5. Conclusions
In order to develop the energy storage unit and H2 storage unit using CaCl2・mNH3 (m = 4, 8) + Ti (weight ratio; Ti/CaCl2 = n, where n = 3) system, the thermophysical properties (effective thermal conductivity ![]()
and effective thermal diffusivity![]()
) as major design factors of energy and H2 storage units were measured by the any heating method. In comparing ![]()
of CaCl2・mNH3 + Ti and CaCl2・mNH3, the value of ![]()
of CaCl2・m NH3 + Ti are approximately 1.5 - 2.2 times larger than those of CaCl2・mNH3. It seems that the effective thermal conductivity depends on the bulk density.
Regarding ![]()
of CaCl2・mNH3 + Ti and CaCl2・mNH3, the value of ![]()
of CaCl2・mNH3 + Ti is approximately 1.3 - 1.5 times larger than those of CaCl2・mNH3. It is found that the addition of the heat transfer media (Ti) is an effective way for the improvement of effective thermal conductivity and the thermal diffusivity of this reaction system and it is possible to control the reaction rate.
It reveals that the thermophysical properties in this measurement would be the valuable design factors to develop energy and H2 storage systems utilizing natural resources such as solar energy.
Nomenclature
![]()
Constant of
Laplace
integration (-)
![]()
Constant of
Laplace
integration (-)
![]()
Zero order modified
Bessel
functions of the first kind
![]()
Zero order modified
Bessel
functions of the second kind
![]()
Heat flux (W/m2)
![]()
Laplace integration of ![]()
(-)
![]()
Distance of radius direction (mm)
![]()
Laplace parameter (-)
![]()
Time (s)
![]()
Temperature (K)
Greek letters
![]()
Thermal diffusivity and effective thermal diffusivity (m2/s)
ΔH Enthalpy change
![]()
Thermal conductivity and effective thermal conductivity (W/(m・K))
![]()
Bulk density (kg/m3)
![]()
Temperature difference (K)
![]()
Laplace integration of ![]()
(-)
Subscripts
i Measurement point (i = 0, 1, 2, 3, 4)
[I] Hollow cylindrical sample and Reference specimen
[II] Cylindrical sample and Measured specimen
NOTES
*Corresponding author.