On the Stability of Solutions of Nonlinear Functional Differential Equation of the Fifth-Order ()

1. Introduction
As is well-known, the area of differential equations is an old but durable subject, that remains alive and useful to a wide variety of engineers, scientists and mathematicians. Now the subject of differential equations represents a huge body of knowledge including many subfields and a vast array of applications in many disciplines. It should be noted that principles of differential equations are largely related to the qualitative theory of ordinary differential equations. Qualitative theory refers to the study of behaviour of solutions, for example, the investigation of stability, instability, boundedness of solutions and etc., without determining explicit formulas for the solutions. In particular one can refer that many authors have dealt with delay differential equations and its problems, and many excellent results have been obtained on the behaviour of solutions for various higher-order: second-, third-, fourth-, and fifth-order nonlinear differential equations with delay, for example, [1] -[27] , and references quoted therein, which contain the differential equations without delay or with delay. In many of these references, the authors dealt with the problems by using Lyapunov’s second method [28] . By considering Lyapunov functionals we obtained the conditions which ensured the stability of the problem. It is worth-mentioning that construction of these Lyapunov functionals remains a general problem. We know that a similar problem exists for ordinary differential equations for higher-order [12] . Clearly, it is even more difficult to construct Lyapunov functionals for delay differential equations of higher-order. Up to this moment the investigations concerning the stability of solutions of nonlinear equations of fifth-order with delay have not been fully developed.
In particular in 2010 Tunç [29] obtained sufficient conditions, which ensure the stability of the zero solution of a nonlinear delay differential equation of fifth-order

where  and f are continuous functions;
and f are continuous functions;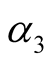 ,
, 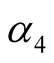 and
and 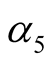 are positive constants, r is a bounded delay and positive constant; the derivatives
are positive constants, r is a bounded delay and positive constant; the derivatives  exist and are continuous for all z, w and
exist and are continuous for all z, w and .
.
Later in 2011 Abou-El-Ela, Sadek and Mahmoud [30] obtained the sufficient conditions for the uniform stability of the zero solution of a nonlinear fifth-order delay differential equation of the following form
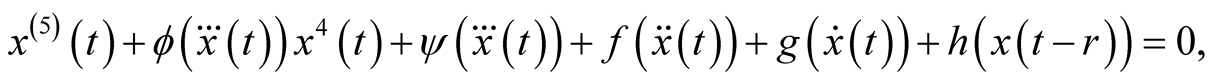
where 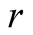 is a positive constant;
is a positive constant;  and
and  are continuous functions and
are continuous functions and 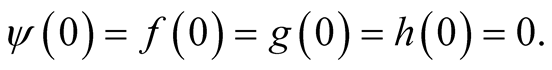
In the present paper, we are concerned with the stability of the zero solution of the fifth-order nonlinear delay differential equation on the form
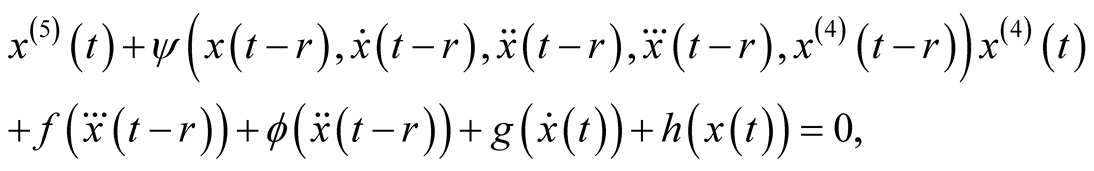 (1.1)
(1.1)
or its equivalent system form
 (1.2)
(1.2)
where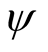 ,
, 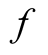 ,
, 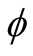 ,
, 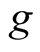 and
and  are continuous functions for the arguments displayed explicitly in (1.1) with
are continuous functions for the arguments displayed explicitly in (1.1) with 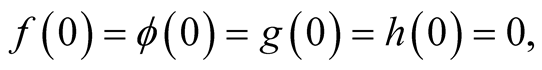 r is a bounded delay and positive constant; the derivatives
r is a bounded delay and positive constant; the derivatives  and
and  exist and are continuous for all
exist and are continuous for all .
.
2. Preliminaries and Stability Results
In order to reach the main result of this paper, we will give some basic information to the stability criteria for the general autonomous delay differential system. We consider
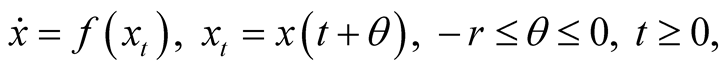 (2.1)
(2.1)
where 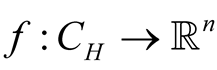 is a continuous mapping,
is a continuous mapping, 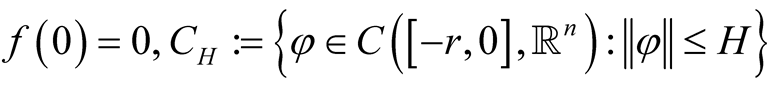 and for
and for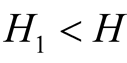 , there exists
, there exists 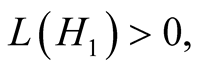 with
with 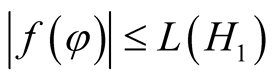 when
when 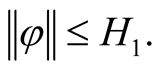
The following are the classical theorems on uniform stability and global asymptotic stability for the solution of (2.1).
Theorem 2.1. [31] . Let 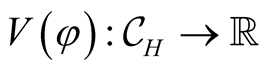 be a continuous functional satisfying a local Lipschitz condition
be a continuous functional satisfying a local Lipschitz condition  and the functions
and the functions  are wedges such that i)
are wedges such that i)  and ii)
and ii) .
.
Then the zero solution of (2.1) is uniformly stable.
Theorem 2.2. [32] . Suppose , let V be a continuous functional defined on
, let V be a continuous functional defined on 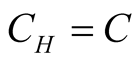 with
with , and let
, and let  be non-negative and continuous function for
be non-negative and continuous function for ,
,  as
as  such that for all
such that for all 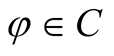
i) ,
, 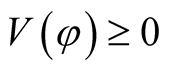 and ii)
and ii) 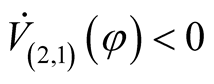 for
for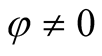 .
.
Then all solutions of (2.1) approach zero as 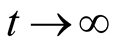 and the origin is globally asymptotically stable.
and the origin is globally asymptotically stable.
The following will be our main stability result for (1.1).
Theorem 2.3. In addition to the basic assumptions imposed on the functions 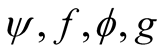 and h. Suppose that the following conditions are satisfied, where
and h. Suppose that the following conditions are satisfied, where 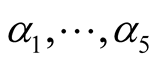 are arbitrary positive constants and
are arbitrary positive constants and 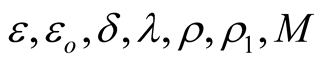 and L are sufficiently small positive constants i)
and L are sufficiently small positive constants i) 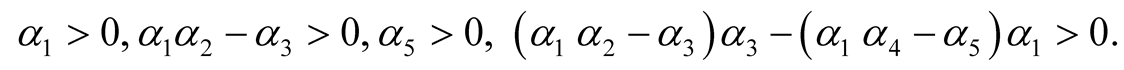
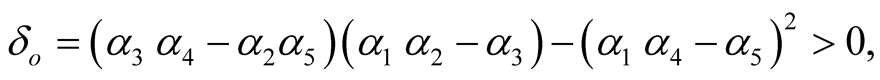 (2.2)
(2.2)
and the following two inequalities
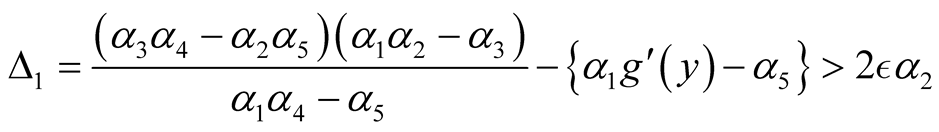 (2.3)
(2.3)
 (2.4)
(2.4)
for all 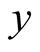 and all
and all 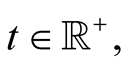 where
where

ii) 
iii) 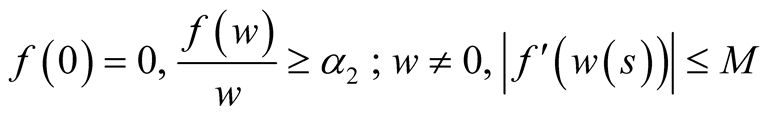 and
and

iv)  and
and
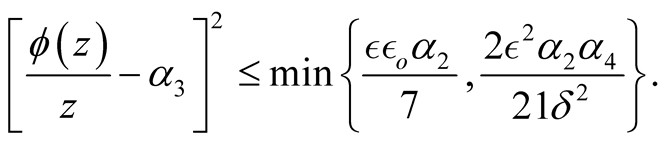
v)  and
and
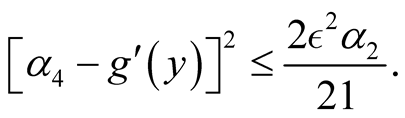
vi) 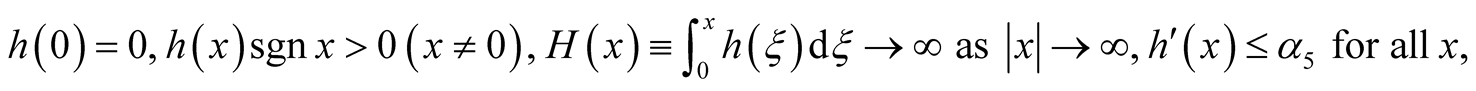 and
and
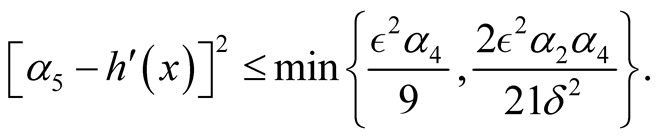
Then the zero solution of (1.1) is globally asymptotically stable, provided that
 .
.
Proof. We define the Lyapunov functional 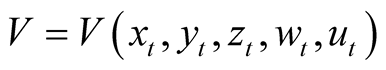 as:
as:
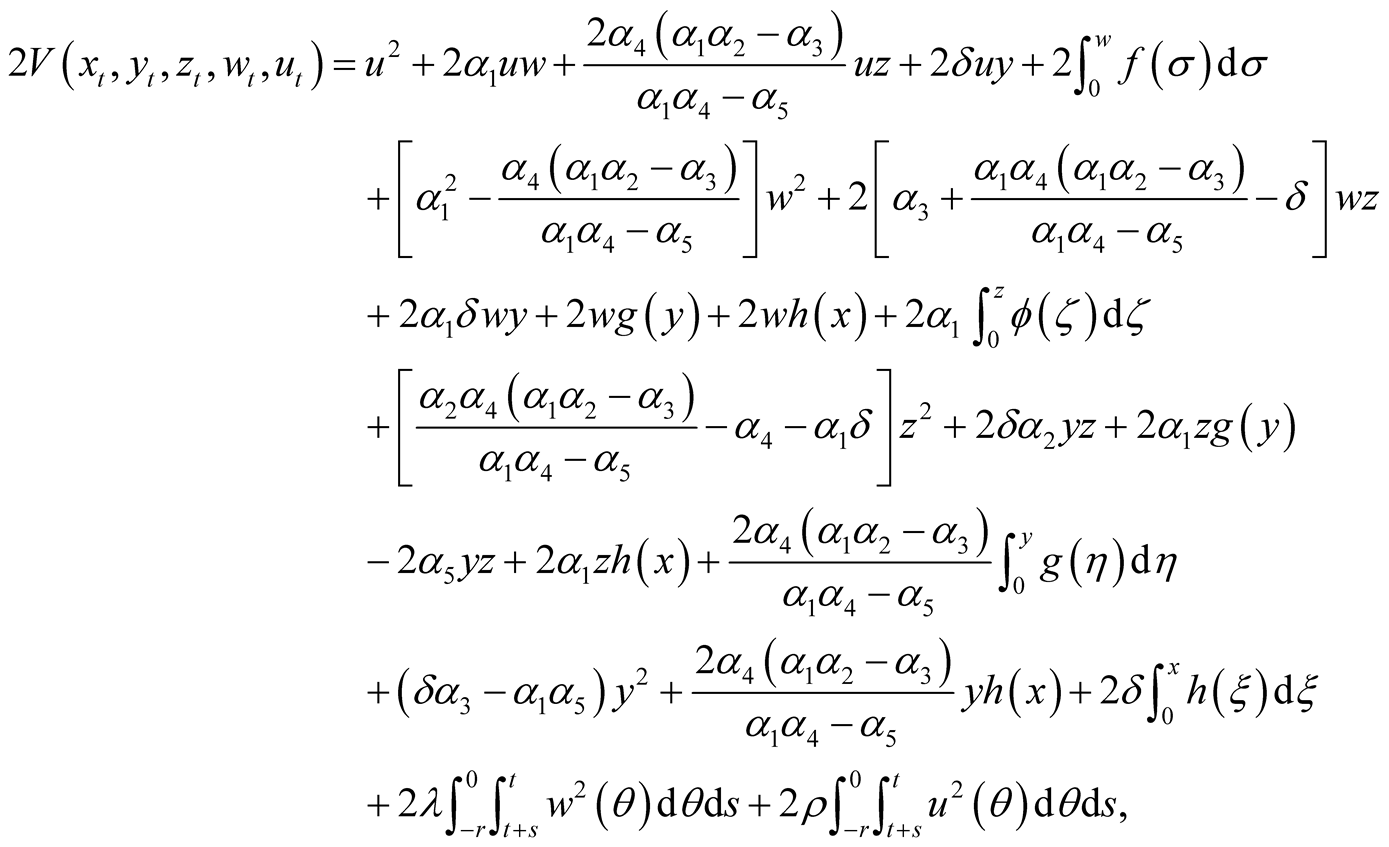 (2.5)
(2.5)
where 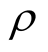 and
and  are two positive constants, which will be determined later and
are two positive constants, which will be determined later and 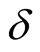 is a positive constant defined by
is a positive constant defined by
 (2.6)
(2.6)
Then it is convenient to rewrite the expression for the Lyapunov functional defined in (2.5) in the following form
 (2.7)
(2.7)
where

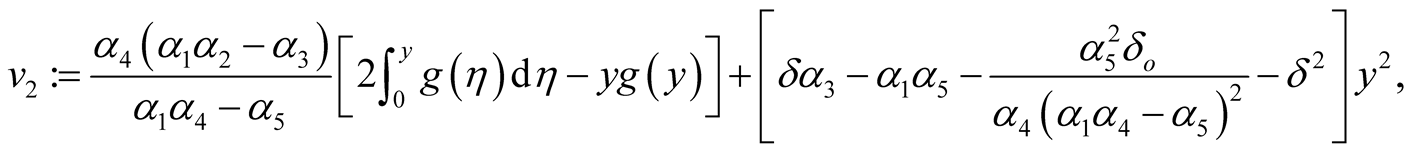

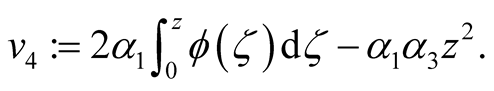
For the component , by using (2.6) and the definition of
, by using (2.6) and the definition of 

since 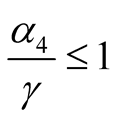 by v), thus we obtain
by v), thus we obtain
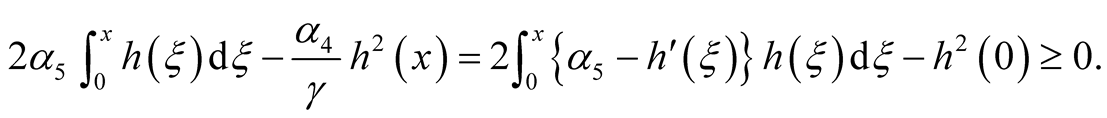
This is due to the fact that the integral on the right-hand side is non-negative by vi), therefore we get

From the identity

therefore
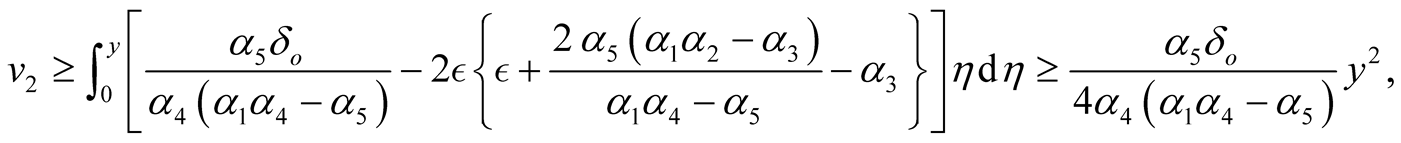
and by using v) we find
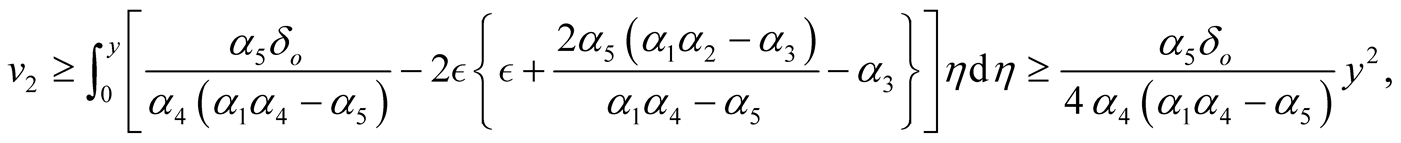
provided that


From iv) we find
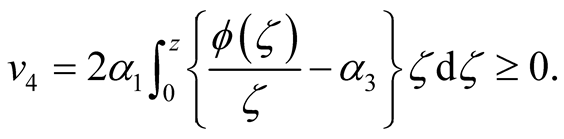
Summing up the four inequalities obtained from  into (2.7), we have
into (2.7), we have
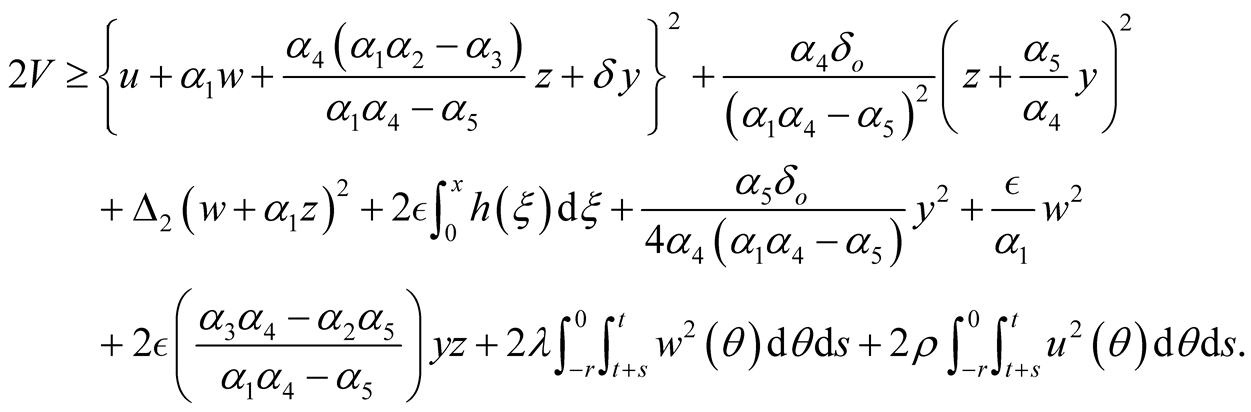 (2.8)
(2.8)
Clearly, it follows from the first six terms included in (2.8) that there exist sufficiently small positive constants  such that
such that
 (2.9)
(2.9)
Now we consider the terms
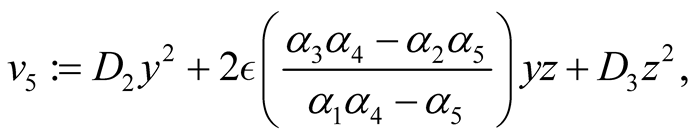
which are contained in (2.9) and by using the inequality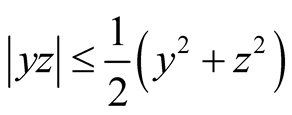 , we obtain
, we obtain

for some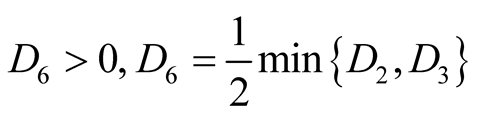 , if
, if

By using the previous inequality, we get from (2.9) that
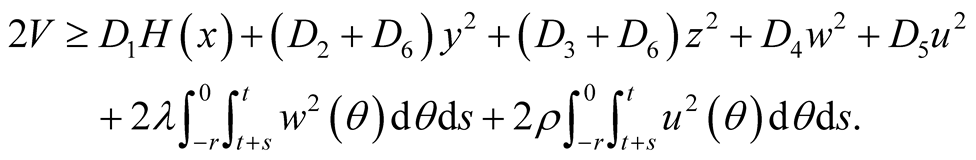 (2.10)
(2.10)
As a result, since the integrals
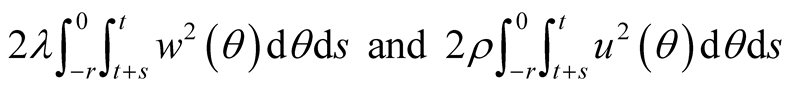
are non-negative, it is obvious that there exists a positive constant 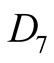 which satisfies the following inequality
which satisfies the following inequality
 (2.11)
(2.11)
where
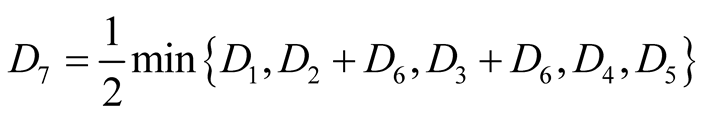 .
.
Now by a direct calculation from (1.2) and (2.5) one finds
 (2.12)
(2.12)
Making use of the assumptions ii)-vi), (2.3) and (2.6), we get


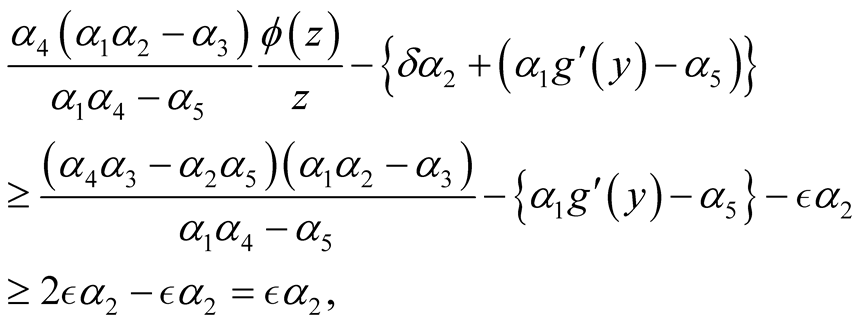
and

By v), vi) and (2.6).
By using the assumptions  and
and 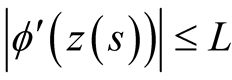 of the theorem and inequality
of the theorem and inequality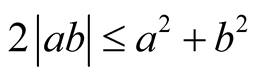 , we obtain the following inequalities
, we obtain the following inequalities
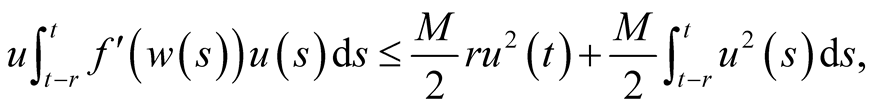

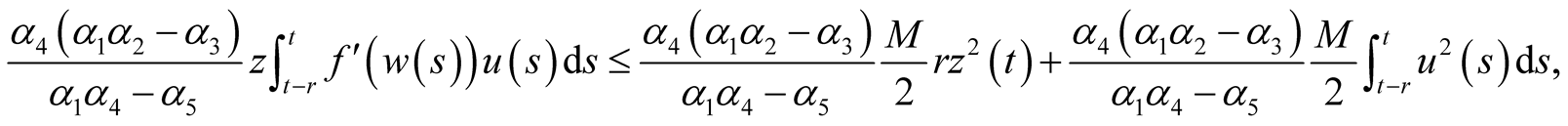

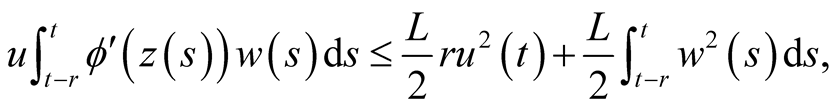


and

Replacing the last equality and the preceding inequalities into (2.12), we obtain
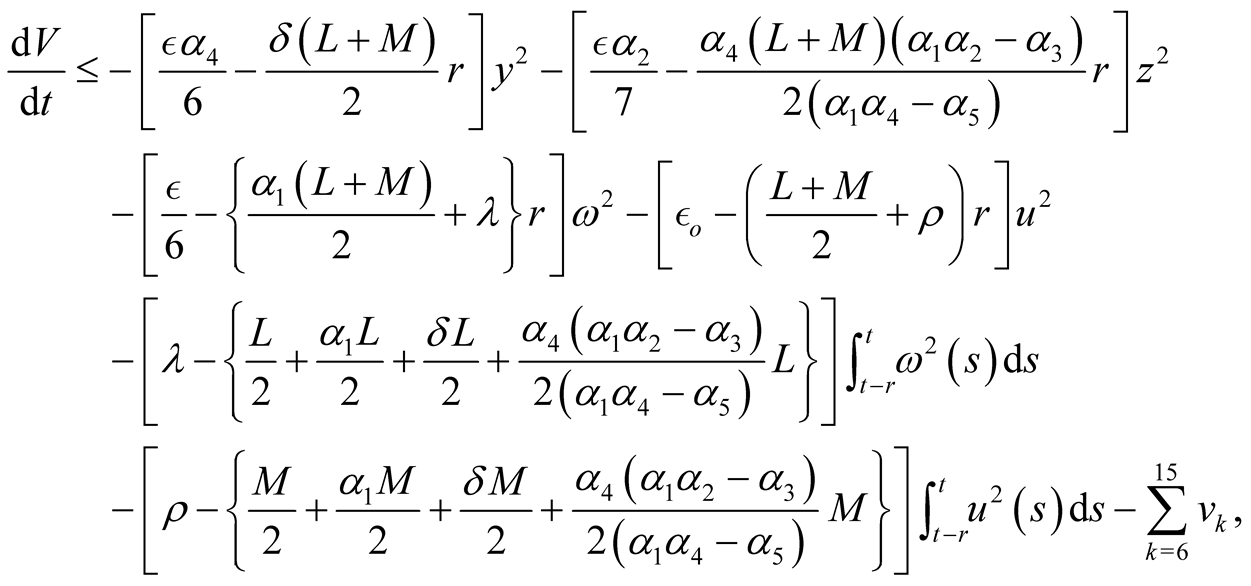 (2.13)
(2.13)
where
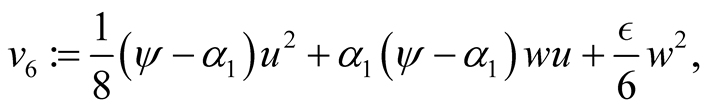

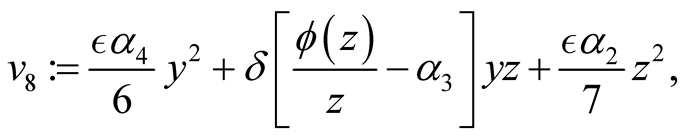
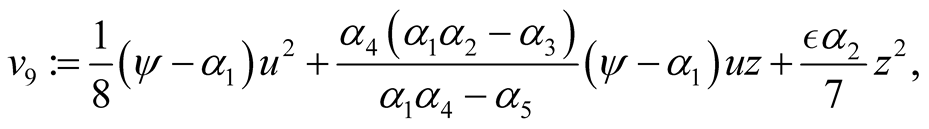


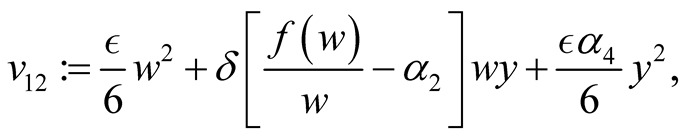
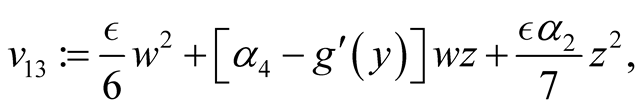
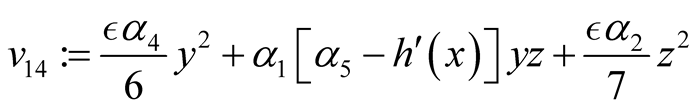
and

It is clear that the expressions given by 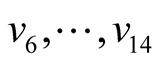 and
and  represent certain specific quadratic forms, respectively.
represent certain specific quadratic forms, respectively.
Making use of the basic information on the positive semi-definite of a quadratic form, one can easily conclude that ,
,  ,
, 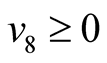 ,
, 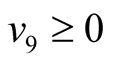 ,
, 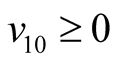 ,
, 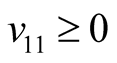 ,
,  ,
, 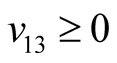 ,
, 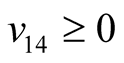 and
and 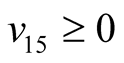 provided that
provided that
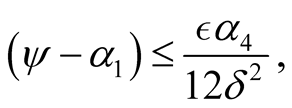



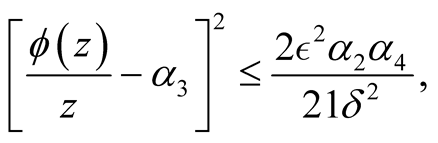
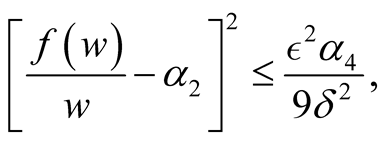

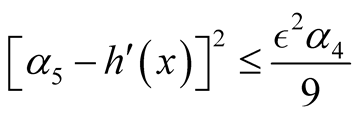
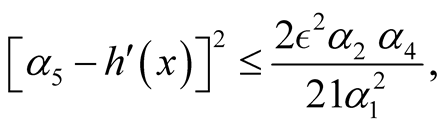
and

respectively.
Thus in view of the above discussion and inequality (2.13), it follows that
 (2.14)
(2.14)
So we can choose the constants 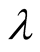 and
and  as the following
as the following

and

then the inequality in (2.14) implies that
 (2.15)
(2.15)
Hence one can easily get from (2.15) that
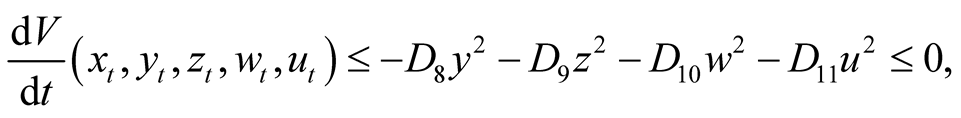 (2.16)
(2.16)
for some positive constants , provided that
, provided that

Finally, it follows that 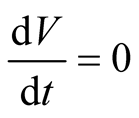 if and only if
if and only if 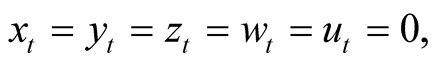
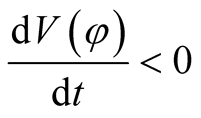 for
for 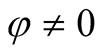 and
and 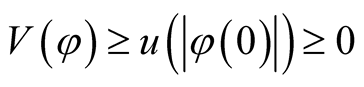 .
.
Thus all the conditions of Theorem 2.2 are satisfied. This shows that the zero solution of (1.1) is globally asymptotically stable.
Then the proof of Theorem 2.3 is completed.