Questions on Optimization of Measurement of Total Electron Content in Ionosphere with GPS ()
1. Introduction
It is well-known that the measurements of total electron content (TEC) and scintillation parameters of ionosphere can be carried out with GPS which is important for study of this layer of atmosphere.
The measurement of said parameters of ionosphere was carried out during last 20 years, but accuracy of such measurements was not so high. Increase of accuracy of said measurements is important from the view point of modification of monitoring of ionosphere and is vital for study of non-stability and turbulence of ionospheric plasma.
As it is noted in the work [1] , the distortions of results of GPS measurements caused by ionosphere factors are one of the most significant components of total error of positioning using GPS. Delay of GPS signals due to effect of ionospheric electrons can be featured and taken account by carrying out double frequency measurements, signed as GPS 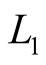 and
and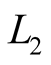 .
.
2. Critical Review of Existing Methods
According to [1] , if the frequency of the GPS signal too exceeds the frequency of ionospheric plasma, the group delay 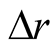 measured by meters, should be defined as:
measured by meters, should be defined as:
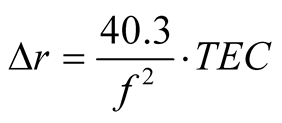 , (1)
, (1)
where TEC—total electronic content (electrons per square meter);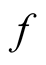 —frequency of GPS signal.
—frequency of GPS signal.
It should be noted, that one unit of TEC, equal to 1016 electron∙m−2 causes delay of 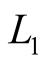 equal to 0.163 m, and
equal to 0.163 m, and 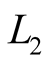 −0.267 m.
−0.267 m.
According to [1] , the following interrelation of major parameters used in double frequency measurements of TEC does exist,
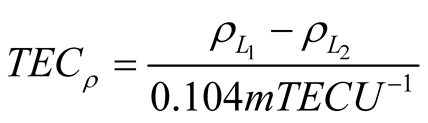 , (2)
, (2)
where 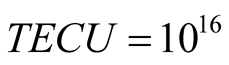 electron∙m−2;
electron∙m−2; 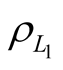 and
and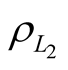 —measured pseudo ranges.
—measured pseudo ranges.
It should be noted, that the Formula (2) is true for carrying out of GPS code measurements.
As it is noted in [1] , the total electron content in ionosphere also can be determined by carrying out the measurements of phase of carrier signal of 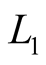 and
and . If that, the following formula is true,
. If that, the following formula is true,
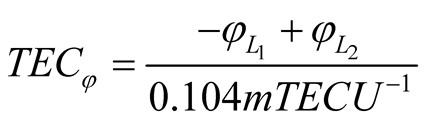 , (3)
, (3)
where  and
and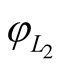 —phases of signals
—phases of signals 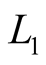 and
and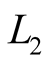 , transformed to ranges.
, transformed to ranges.
In order to calculate the resulting values of 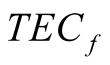 the following algorithm is suggested in [1] :
the following algorithm is suggested in [1] :
The averaged value of difference 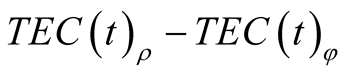 as a function of time should be calculated using least squares method,
as a function of time should be calculated using least squares method,
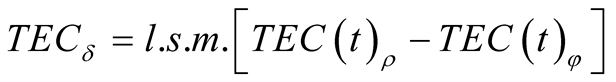 . (4)
. (4)
The final value of difference 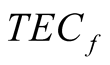 should be determined as:
should be determined as:
 . (5)
. (5)
According to [1] , the above described method allows to calculate the smoothed and absolute amount of  in link with each satellite during whole time of its functioning.
in link with each satellite during whole time of its functioning.
At the same time, such method of calculation of TEC in ionosphere is non-effective due to following reasons. As it is noted in the work [2] , the disperse nature of ionosphere causes the temporal delay inversely proportional to square of frequency of radio signal. This, in principle, allows removing the ionospheric error during geodetic GPS measurements carrying out combinational double frequency method of positioning. In this case, the above said dispersive property is strictly observed in the Formula (1). According to this formula the group delay should be more at the frequency 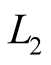 (we remind, that
(we remind, that 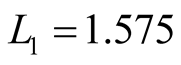 GHs;
GHs;  GHs).
GHs).
In line with works [3] -[5] , the signal/noise ratios for frequencies 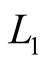 and
and  are sharply different. Upon use of radio occultation method the signal/noise ratios of received GPS signals are not constant temporally due to defocusing and/or attenuation of radio signal. The difference between signal/noise ratios for
are sharply different. Upon use of radio occultation method the signal/noise ratios of received GPS signals are not constant temporally due to defocusing and/or attenuation of radio signal. The difference between signal/noise ratios for  and
and 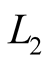 frequencies is not less than 15% - 20% and can reach 100% and more.
frequencies is not less than 15% - 20% and can reach 100% and more.
Taking into account such a significant difference between signal/noise ratios for 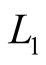 and
and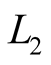 , the method described in [1] , based on of Formulas (2)-(5), can be considered as non-rational, because this method provides for carrying out of joint statistical processing of signal featured by different level noisiness.
, the method described in [1] , based on of Formulas (2)-(5), can be considered as non-rational, because this method provides for carrying out of joint statistical processing of signal featured by different level noisiness.
Authors of the work [6] suggest taking into account the different level of noises in  and
and 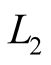 signals in GPS occultation measurements by calculating the linear combination of these signals. It is noted, that custom linear combination of
signals in GPS occultation measurements by calculating the linear combination of these signals. It is noted, that custom linear combination of 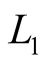 and
and 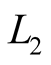 is functioning well only if noises are miserable. But, in reality the quality of signal
is functioning well only if noises are miserable. But, in reality the quality of signal 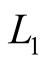 is more higher, than that of
is more higher, than that of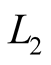 , which commonly is not taken into account in such linear combinations.
, which commonly is not taken into account in such linear combinations.
Authors of [6] suggest to develop such a combination of signals, which would take into account the different levels of their noisiness. In this case 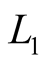 and
and 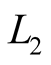 should be processed independently each other. The weight coefficients of these components accord to their estimated dynamic accuracy. It is noted, that such a method allows increasing the total effectiveness of radio occultation method.
should be processed independently each other. The weight coefficients of these components accord to their estimated dynamic accuracy. It is noted, that such a method allows increasing the total effectiveness of radio occultation method.
3. Optimization of Measuring of TEC in Ionosphere Using GPS
The purpose of the present article is further development of idea, suggested in [6] concerning independent processing of 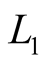 and
and 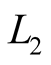 signals by way of optimization of the measurement process using the limitation condition imposed on general resources of measuring operations.
signals by way of optimization of the measurement process using the limitation condition imposed on general resources of measuring operations.
As it was noted above, in line with the method, suggested in [1] , the average value of 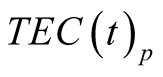 and
and 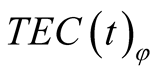 should be calculated using formula [4] . In its turn, to calculate the average value of
should be calculated using formula [4] . In its turn, to calculate the average value of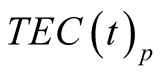 , in line with Formula (2), the average values of
, in line with Formula (2), the average values of 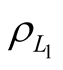 and
and 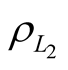 should be calculated.
should be calculated.
But it is well-known that upon calculation of averaged values of noisy measuring signals the random error of measurement decreases by 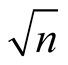 times, where
times, where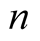 –number of measurements.
–number of measurements.
The task of optimal organization of measurement upon realization of above described method can be formulated as follows. Assume, that the limitation condition is imposed on total number amount of carried out measurement operations by purpose to calculate the average values of 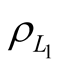 and
and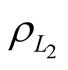 , i.e. the number of measurement operations is limited and equal to
, i.e. the number of measurement operations is limited and equal to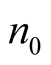 .
.
Let us signify the random error of measurement of 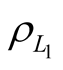 as
as 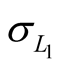 and
and 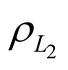 as
as .
.
The total random error of measuring of  can be determined as:
can be determined as:
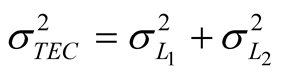 . (6)
. (6)
If we assume, that  should be measured by
should be measured by 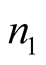 times, then
times, then 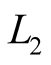 may be measured by
may be measured by  times. Therefore, the total random error can be determined as:
times. Therefore, the total random error can be determined as:
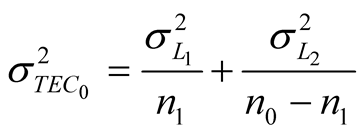 . (7)
. (7)
Now we are searching for minimum of function (7) on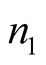 .
.
The first derivative of function (7) on  gives us:
gives us:
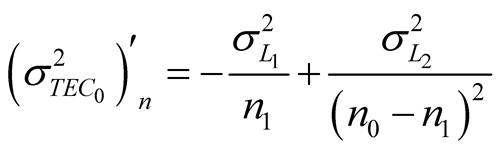 . (8)
. (8)
Taking into account
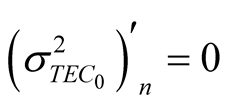
we get:
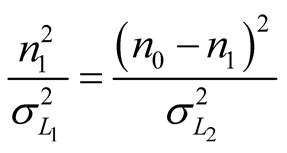 . (9)
. (9)
From the Formula (9) it is easy to get following square order linear equation:
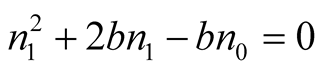 . (10)
. (10)
where
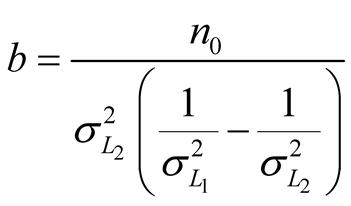 . (11)
. (11)
Solution of Equation (10) is following:
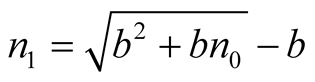 . (12)
. (12)
Using method of second derivative we can show, that upon solution (12) the total random error reaches its minimum value. The second derivative of Equation (7) is as follows:
 . (13)
. (13)
As it can be seen from Formula (13) the second derivative is always positive, which confirm the solution (12).
Therefore, it is shown, that if the limitation is imposed on total number of possible measurements of  we should take into account, that the minimum value of total random error of this parameter can be reached upon different numbers of measurements of
we should take into account, that the minimum value of total random error of this parameter can be reached upon different numbers of measurements of 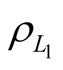 and
and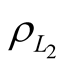 .
.
Due to simmetricity of Formulas (2) and (3) the similar conclusion is true for case of measuring .
.
4. Conclusions
Consequently, it is shown that upon imposed limitation on total number of carried out measurements, due to different values of signal/noise ratios of 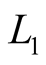 and
and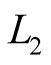 , the minimum value of random errors
, the minimum value of random errors  and
and 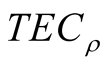 can be obtained upon non-equal numbers of measurements of parameters
can be obtained upon non-equal numbers of measurements of parameters  and
and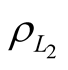 , and
, and 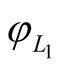 and
and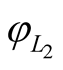 . It is obvious that minimization of total random of
. It is obvious that minimization of total random of 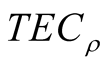 and
and  could lead to an increase of accuracy of resulting value of
could lead to an increase of accuracy of resulting value of , which is the main output parameter of the known method [1] , designated for calculation of total electron content in ionosphere.
, which is the main output parameter of the known method [1] , designated for calculation of total electron content in ionosphere.
In conclusion we can formulate following results of research carried out:
The analysis of existing method for calculation of total electron content in ionosphere using the GPS occultation measurements does show that due to different values of signal/noise ratios for GPS signals  and
and 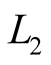 the special method of optimal measurements of frequency components of TEC measured by phase and code measurements methods should be developed.
the special method of optimal measurements of frequency components of TEC measured by phase and code measurements methods should be developed.
The optimal number of measurements of above said frequency components is determined taking into account the limitation condition imposed on total number of measurements carried out.