1. Introduction
Möbius transformations have applications to problems in physics, engineering and mathematics. Furthermore, the conformal mapping is represented as bilinear translation, linear fractional transformation and Mobius transformation.
Möbius transformations are also called homographic transformations, linear fractional transformations, or fractional linear transformations and it is a bijective holomorphic function (conformal map) [1] [2] .
The purpose of this paper is studied the properties of Möbius transformations in detail, and some definitions and theorems are given. The basic properties of these transformations are introduced and classified according to the invariant points. Möbius transformations are formed a group action PSL (2,Â) on the upper half plane model.
A Möbius transformation of the plane is a map f: 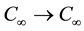
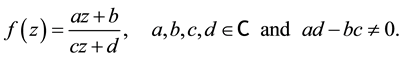 (1-1)
(1-1)
which sending each point to a corresponding point, where z is the complex variable and the coefficients a, b, c, d are complex numbers [3] .
Definition (1-1).
The upper half plane model is defined by the set
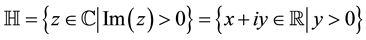 (1-2)
(1-2)
and the boundary of is defined by
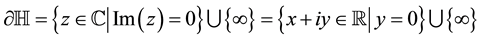 (1-3)
(1-3)
The lines (geodesics) are vertical rays and semicircles orthogonal to ¶H. The angles are Euclidean angles.
Definition (1-2).
A Möbius transformations form a group which is denoted by .
.
Remark (1-3).
Since Möbius transformation takes the form 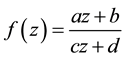
If the point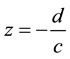 , this means
, this means  so
so 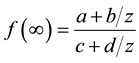 and we get the following:
and we get the following:
1) 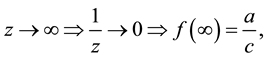
2) If c = 0 
3) If 
Lemma (1-4).
A Möbius transformation consists of four composition functions.
Proof.
The four functions are:
1) translation by 
2) inversion and reflection with respect to real axis  then the plane inside turn out and the lines on the plane are lines or circles and right angles stay true and also the circles are circles;
then the plane inside turn out and the lines on the plane are lines or circles and right angles stay true and also the circles are circles;
3) dilation and rotation 
4) translation by 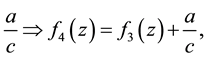
![]() (1-4)
(1-4)
Remark (1-5).
We can write Möbius transformations as follows
![]() (1-5)
(1-5)
The inverse Möbius transformation is evaluated from the inverse of the metric
![]()
then
![]() (1-6)
(1-6)
Theorem (1-6).
Möbius transformations also preserve cross ratio.
Proof.
Given four distinct points z1, z2, z3, z4, their cross ratio is defined by
![]() (1-7)
(1-7)
The cross ratio is invariant of the group of all Möbius transformation so if we transform the four points zi into ![]() by an inversion, the cross ratio of these points are taken into its conjugate value, and the cross ratio is invariant under a product of two or any even number of inversions and exchanging any two pairs of coordinates preserves the cross-ratio. Then
by an inversion, the cross ratio of these points are taken into its conjugate value, and the cross ratio is invariant under a product of two or any even number of inversions and exchanging any two pairs of coordinates preserves the cross-ratio. Then
![]() (1-8)
(1-8)
Since translation, rotation and dilation preserve cross ratio and Möbius transformation consists of them so Möbius transformation preserves cross ratio.
Corollary (1-7).
![]() (1-9)
(1-9)
If![]() , we get
, we get
![]() (1-10)
(1-10)
and therefore
![]() (1-11)
(1-11)
If any one of zi = 0 for example z3 = 0, then
![]() (1-12)
(1-12)
Since the trace of matrix A is tr(A) = a + b and this trace is invariant under conjugation, this is mean,
![]() . (1-13)
. (1-13)
Every Möbius transformation can be represented by normalized matrix A such that its determinant equal one which mean ad − bc = 1.
Lemma (1-8).
Two Möbius transformations A, B with ![]() are conjugate if and only if
are conjugate if and only if
![]() . (1-14)
. (1-14)
Poof.
Let ![]()
Since matrix A and B are Möbius transformations, then
![]()
![]()
Since![]() , then
, then
![]()
![]()
If and only if ![]() then matrix A and matrix B must be conjugate.
then matrix A and matrix B must be conjugate.
2. The Fixed Points in Mobius Transformation
A Möbius transformation is ![]()
Since fixed points (i.e. invariant points) is defined by f(z) = z, then ![]()
This mean![]() , then the fixed points are given by
, then the fixed points are given by
![]() (1-15)
(1-15)
For non parabolic transformation, there are two fixed points 0, ¥ but for parabolic transformation, there is only fixed points ¥ because the fixed points are coincide.
3. The Types of Mobius Transformations
There are Parabolic, elliptic, hyperbolic and loxodromic which are distinguished by looking at the trace tr(A) = a + b.
3.1. For Parabolic Transformations
tr2(A) = 4, the parabolic Möbius transformations forms subgroup isomorphic to the group of matrices ![]() [4] ,
[4] ,
![]() , (1-16)
, (1-16)
which describes a translation ![]() and this transformation is orientation preserving.
and this transformation is orientation preserving.
3.2. For Hyperbolic Transformations
![]() , the hyperbolic Möbius transformations forms subgroup isomorphic to the group of matrices
, the hyperbolic Möbius transformations forms subgroup isomorphic to the group of matrices ![]()
![]() , (1-17)
, (1-17)
which describes a rotation ![]() and this transformation is orientation preserving.
and this transformation is orientation preserving.
3.3. For Elliptic Transformations
![]() , the elliptic Möbius transformations forms subgroup isomorphic to the group of matrices
, the elliptic Möbius transformations forms subgroup isomorphic to the group of matrices ![]()
![]() , (1-18)
, (1-18)
which describes a rotation ![]() and this transformation is orientation preserving.
and this transformation is orientation preserving.
3.4. For Loxodromic Transformations
![]() , the Loxodromic Möbius transformations forms subgroup isomorphic to the group of matrices
, the Loxodromic Möbius transformations forms subgroup isomorphic to the group of matrices![]() ,
,
![]() , (1-19)
, (1-19)
which describes a dilation (homothety) ![]() and this transformation is orientation preserving.
and this transformation is orientation preserving.
The difference between orientation preserving (invariant) and orientation reversing:
1) Rotation and translation are orientation-preserving.
2) Reflection and glide-reflection are orientation-reversing.
3) A composition of orientation-preserving functions is orientation-preserving.
4) A composition of two orientation-reversing functions is orientation-preserving.
5) A composition of one orientation-preserving function and one orientation-reversing function is orientation- reversing.
6) The determinant of the matrix A = 1 (which mentioned above) then the orientation-preserving but if the determinant of the matrix A = ‒1 then the orientation reversing
7) ![]() such that
such that ![]() is orientation-preserving but
is orientation-preserving but ![]() with
with ![]() is orientation-reversing, where
is orientation-reversing, where ![]() which mean the point z in the imaginary axis.
which mean the point z in the imaginary axis.
8) In Orientation preserving all non collinear points A, B, C, the proper angle measures of the angles ABC and A'B'C' have the same sign but in orientation reversing all non collinear points A, B, C, the proper angle measures of the angles ABC and A'B'C' have opposite signs.
9) Orientation preserving isometries takes counterclockwise angles to counterclockwise angles, and it takes clockwise angles to clockwise angles. An orientation reversing isometries takes counterclockwise angles to clockwise angles, and it takes clockwise angles to counterclockwise angles.
4. Isometries in Mobius Transformation
Definition (4-1).
The group ![]() [4] is the projective special linear group of dimension 2 over the real numbers and the determinant of the elements of that group may be 1 or −1 so
[4] is the projective special linear group of dimension 2 over the real numbers and the determinant of the elements of that group may be 1 or −1 so ![]() and this group act on
and this group act on
by Möbius transformations and also the matrices of this group conjugate to the matrix ![]() such
such
that ![]() from the Jordan and normal form of a real 2 by 2 matrix and therefore the determinants of these matrices must equal 1, we can see that the absolute value of the traces
from the Jordan and normal form of a real 2 by 2 matrix and therefore the determinants of these matrices must equal 1, we can see that the absolute value of the traces ![]() of the matrices will be respectively less than 2, called elliptic, greater than 2, called hyperbolic, and equal to 2, called parabolic.
of the matrices will be respectively less than 2, called elliptic, greater than 2, called hyperbolic, and equal to 2, called parabolic.
Definition (4-2).
Let ![]() be path so the hyperbolic distance between two points (a, b) on the upper half plane
be path so the hyperbolic distance between two points (a, b) on the upper half plane
with metric ![]() is defined by
is defined by ![]() which can be written as
which can be written as
![]() (1-20)
(1-20)
Remark (4-3).
From this definition the geodesic between two points (x0, y1) and (x0, y2) on the vertical line with y2 > y1 has length ln(y2/y1) but if two points do not lie on a vertical line so the geodesics is circular arc with center on the x-axis as seen in Figure 1.
Remark (4-4).
From the definition (1-1) we can define the isometry of hyperbolic plane ![]() as follows:
as follows:
Let a mapping f: ![]() and let A and B two points in
and let A and B two points in![]() , the mapping f is an isometry if the hyperbolic distance
, the mapping f is an isometry if the hyperbolic distance![]() .
.
Theorem (4-4).
Möbius transformations act isometries in ![]() this mean
this mean ![]() acts isometry on upper half plane
acts isometry on upper half plane ![]() by Möbius transformations.
by Möbius transformations.
Proof.
Möbius transformations preserve distance. A bijective map that preserves distance is called an isometry because an isometry is a transformation which preserves distance. Thus Möbius transformations are isometries of H.
A second proof.
Since the form of Möbius transformations are![]() , differentiate this form yields to
, differentiate this form yields to ![]() .
.
Since
![]()
Then
![]() (1-21)
(1-21)
From this equation we remark that Möbius transformations preserve the hyperbolic metric so that Möbius transformations are hyperbolic isometries.
A third proof.
From the definition of hyperbolic distance, we want to show that![]() .
.
Since ![]() so the hyperbolic metric
so the hyperbolic metric ![]() is defined by
is defined by![]() , since the right hand side
, since the right hand side
![]()
Figure 1. The plane as boundary of half space model of hyperbolic space.
![]() (1-22)
(1-22)
Let![]() , then
, then
![]() (1-23)
(1-23)
and from![]() , then
, then
![]() (1-24)
(1-24)
Since the left hand side is
![]() (1-25)
(1-25)
Since ![]() and so
and so ![]()
Then
![]() (1-26)
(1-26)
We get the left hand side equal the right hand side, and then the proof is complete.
Lemma (4-5).
Let Mobius transformations![]() , then
, then
![]() . (1-27)
. (1-27)
Proof.
The right hand side ![]() And therefore the left hand side
And therefore the left hand side![]() .
.
We get the left hand side equal the right hand side, and then the proof is complete.
Remark (4-6).
The group ![]() acts on
acts on ![]() by Mobius transformation
by Mobius transformation
![]() (1-28)
(1-28)
This action is faithful and ![]() isomorphic to the group of all orientation preserving isometrics of
isomorphic to the group of all orientation preserving isometrics of ![]() and act discontinuously on
and act discontinuously on ![]() so we can write
so we can write![]() . This mean
. This mean ![]() which preserve the hyperbolic geometry of
which preserve the hyperbolic geometry of ![]() and therefore the elements in Möbius transformation act by isometries in
and therefore the elements in Möbius transformation act by isometries in ![]() [5] .
[5] .
Theorem (4-7).
All orientation-preserving isometries of ![]() are Mobius transformations, and all orientation-reversing isometries of
are Mobius transformations, and all orientation-reversing isometries of ![]() are the composition of a Mobius transformation and reflection through the imaginary axis.
are the composition of a Mobius transformation and reflection through the imaginary axis.
Proof.
The isometry group of hyperbolic plane is denoted by ![]() which identified with the group of Mobius transformations, and the group of orientation preserving isometries which is the distance preserving maps are the Mobius transformations which preserve
which identified with the group of Mobius transformations, and the group of orientation preserving isometries which is the distance preserving maps are the Mobius transformations which preserve ![]() and is denoted by
and is denoted by ![]() which identified with
which identified with ![]() such that
such that ![]() acts on the boundary of the upper half plane by
acts on the boundary of the upper half plane by
![]() (1-29)
(1-29)
and then, we get:
![]() (1-30)
(1-30)
Let f(z) is an isometry of![]() , and by applying the transformations (rotation) z → kz and inversion z → −1/z, we assume that
, and by applying the transformations (rotation) z → kz and inversion z → −1/z, we assume that
![]() (1-31)
(1-31)
Let z1, z2 be two points lie in positive imaginary axis. Let the point z not lie in positive imaginary axis and draw two hyperbolic circles with center z1 and z2 and passing through z, we find these circles intersect in z, ![]() and these circles are mapped into themselves under the isometry
and these circles are mapped into themselves under the isometry ![]() so
so ![]() or z.
or z.
The first case:
If![]() , we get
, we get ![]() such that
such that![]() , which is the orientation re-
, which is the orientation re-
serving isometries is given by the map![]() , that is the reflection in the imaginary axis and by composition this with Möbius transformations. This means all orientation-reversing isometries of
, that is the reflection in the imaginary axis and by composition this with Möbius transformations. This means all orientation-reversing isometries of ![]() are the composition of a Mobius transformation and reflection through the imaginary axis such that the reflections are isometries that have infinitely many fixed lie on the mirror line.
are the composition of a Mobius transformation and reflection through the imaginary axis such that the reflections are isometries that have infinitely many fixed lie on the mirror line.
The second case:
If![]() , we get
, we get ![]() such that
such that![]() , which is the orientation pre-
, which is the orientation pre-
serving isometries is given by the rotation z → kz and inversion z →−1/z. This means all orientation-preserving isometry of ![]() are Mobius transformations and as we know Mobius transformations consist of a rotation inversion and a translation.
are Mobius transformations and as we know Mobius transformations consist of a rotation inversion and a translation.
Theorem (4-8).
Möbius transformations preserve circles and lines (Figure 2).
Proof.
Let the transformation w = 1/z is an inversion and every Möbius transformation (Figure 3) f(z) of the form (1.1) is a composition of finitely many similarities and inversions [6] -[9] .
Since w = u + iv and z = x + iy, then
![]()
Figure 2. Circle-preserving maps from the plane to itself.
![]()
Figure 3. Möbius transformation is composition of multiple inversions.
![]() (1-32)
(1-32)
From the equation of the circle
![]() (1-33)
(1-33)
But if A = 0, it is a line, if![]() , it is a circle.
, it is a circle.
We can write again the Equation (1-33) w.r.t u, v as follows![]() , which is the equation of a circle.
, which is the equation of a circle.
If D = 0, it is a line, if![]() , it is a circle.
, it is a circle.
So Möbius transformations preserve circles and lines.
Remark (4-9).
From the last theorem (1-5), we find that the circle goes through the origin may be mapped to the circle or the line.
Theorem (4-10).
Möbius transformations preserve distance.
Proof.
From theorem (1-2) Möbius transformations act isometries in ![]() and from definition of isometries we get that the distance between any two points in the hyperbolic plane
and from definition of isometries we get that the distance between any two points in the hyperbolic plane ![]() is invariant by Möbius transformations and Möbius transformations preserve circles (from translation and inversion) and angles so Möbius transformations preserve distance.
is invariant by Möbius transformations and Möbius transformations preserve circles (from translation and inversion) and angles so Möbius transformations preserve distance.
5. Conclusion
The properties of Möbius transformations are introduced in detail, and some definitions and theorems are given to show that Möbius transformations are one-to-one, onto and conformal mapping. Also, Möbius transformations map circles to circles and also, map the real line to the real line such that the coefficients a, b, c and d are real. Every orientation-preserving isometrics of the hyperbolic plane is Möbius transformations. Every orientation-reversing isometrics of the hyperbolic plane is a composition of Möbius transformations and reflection. ![]() is a group under composition and Möbius transformations map the upper half-plane to itself bijectively. So Möbius transformation maps vertical straight lines in
is a group under composition and Möbius transformations map the upper half-plane to itself bijectively. So Möbius transformation maps vertical straight lines in ![]() and circles in
and circles in ![]() with real centers to vertical straight lines and circles with real centers. Furthermore, the connections between Möbius transformations, isometries of the hyperbolic plane, and PSL(2; R) are presented.
with real centers to vertical straight lines and circles with real centers. Furthermore, the connections between Möbius transformations, isometries of the hyperbolic plane, and PSL(2; R) are presented.
Acknowledgements
I wish to express my gratitude towards to Professor Dr. William M. Goldman, University of Maryland and Distinguished Scholar-Teacher Professor, Department of Mathematics, for his valuable, guidance, patience and support. I consider myself very fortunate for being able to work with a very considerate and encouraging professor like him.