1. Introduction
We present a fully-coupled, arbitrary Lagrangian-Eulerian (ALE) fluid-structure interaction (FSI) algorithm that uses overset meshes [1] [2] around moving bodies to alleviate the difficulties and computational costs associated with moving mesh algorithms. Overset meshes allow us to accommodate very large structural displacements, including problems where no displacement constraints exist on the solid (e.g., the advection of deformable bodies). The fluid domain is comprised of a stationary background mesh and body-fitted overset meshes for the structural components. It is only these overset meshes that need to be modified in a mesh motion procedure. The overset methodology does bring some computational overhead with it in terms of the computation of interpolations stencils and weights. In this work, we study the benefits associated with the use of overset grids for FSI computations and compare with a standard approach within a single software framework. The benchmark problem of Turek and Hron [3] is used to demonstrate the method and showcase the improvements that overset grids can offer.
Fluid-structure interaction modeling describes the complex interactions between a deformable solid structure with external and/or internal fluid flow. The fluid flow exerts forces on the wetted solid surface to cause deformation, and the resulting structural motion impacts the fluid flow. For such interaction, a two-way coupled model must be used, wherein the fluid flow and the solid deformations mutually affect each other. Moreover, for time-accurate transient models, a fully-coupled approach must be used such that all governing equations are simultaneously satisfied (at least in the appropriate approximate sense) at each discrete time level.
Numerical simulations of transient, fully coupled1 FSI phenomena have been performed by many authors, using a variety of approaches. The common problem that all approaches must overcome is the disparity in the “natural” coordinate frames of the materials: the equations of solid mechanics are cast in the Lagrangian (reference) frame, while fluid dynamics equations are traditionally written in a fixed Eulerian (spatial) configuration. All computational schemes for coupled FSI problems must bridge these two coordinate frames.
One approach to resolving this mathematical discrepancy in the descriptions is to cast all of the governing equations into an Eulerian framework [4] -[9] . This approach is used when very large structural deformations are expected, as the solid can move freely throughout the domain without changing the topology of the discretization. FSI methods of this type are inherently interface-capturing rather than interface-resolving; that is, the fluidsolid interface is not explicitly part of the discretization. Rather, the interface is captured by solving for its position as part of the numerical solution algorithm. The lack of a sharply defined interface makes the method inherently difficult to use for high Reynolds number flows where boundary layer resolution is an important aspect of the simulation.
Fixed grid methods for FSI have a fixed Eulerian grid, and the solid-fluid interface position is solved for as part of the solution procedure. Gerstenberger et al. [10] applied a fixed grid method for moving interfaces with the use of h-adaptive mesh refinement. They also considered hybrid method that is a combination of fixed-grid and ALE formulations, which allowed for different discretizations and solution strategies for the fluid and solid domains. Wall et al. [11] [12] described both advances in ALE methods and new fixed grid methods based on domain decomposition ideas. In particular, advances in fixed-grid methods for FSI through the use of XFEM and Lagrange multiplier techniques was presented in [13] . These methods were applied to higher-order problems in 3D, using either local adaptivity or another method where a layer of deformable (ALE) fluid elements are added to the structures surface. These methods seem to be very promising in terms of computational cost; however, it remains to be seen how the methods work for very high Reynold’s number flows with turbulent boundary layers.
Examples of interface-capturing methods include the immersed boundary method [14] -[18] , the immersed interface method [19] , the fictitious domain method [20] [21] , the mortar finite element method [22] , and the extended finite element method (XFEM) [23] -[25] . These methods are categorized as Eulerian-Lagrangian (EL) methods with the basic premise of use an Eulerian background mesh for the fluid, and a Lagrangian mesh for the solid, thus allowing both domains to reside in their natural mathematical framework. The two descriptions are then coupled by a similar variety of approaches, such as via the use of Lagrange multipliers or penalty methods. The interface must be captured as part of the solution procedure, requiring some mathematical description of the moving boundary. The prototypical example for interface representation is the level-set method [26] -[28] . As with the fully Eulerian methods, the fluid-solid interface can cause numerical difficulties as it cuts the background cells, resulting in decreased accuracy. Boundary layer resolution with these techniques has not been satisfactorily shown in the literature.
Particle methods, such as smoothed particle hydrodynamics (SPH) or the immersed particle method, have also been applied to coupled FSI problems; see, e.g., [29] -[31] and the references therein for descriptions of these methods. A meshless finite element method with a purely Lagrangian description of both the solid and the fluid was proposed in [32] [33] .
Arbitrary Lagrangian-Eulerian methods, first studied in [34] -[38] and summarized in [39] , allow the mesh topology to remain fixed in an Eulerian manner, move with material particles in a Lagrangian manner, or arbitrarily move to enable capturing of the fluid-solid interface. Tezduyar et al. [40] describe the advantage of the ALE approach over the fixed-mesh alternatives is the ability to maintain high-quality meshes near the structure’s interface, resulting in more accurate fluid mechanics in that region. This reason is especially important for boundary layer resolution. The ALE formulation of the governing equations represents the discretized fluid domain as an arbitrarily deforming mesh, subject to displacement constraints at the fluid-solid interface. The solid equations are solved in Lagrangian coordinates, while the fluid equations are solved on the “moving mesh”. Velocity and traction continuity is enforced across the fluid-solid interface, as well as the kinematic constraint between solid and mesh displacements.
The ALE approach has been used for problems with large structural displacements [41] , for partitioned [42] - [45] or monolithic [46] -[48] coupling strategies, with space-time finite elements [49] [50] , with discontinuous Galerkin methods [51] [52] , and with many other permutations of structural models and numerical approximation types. Two approaches that seem to be popular are the isogeometric analysis method and space-time finite elements. Bazilevs et al. [53] -[55] use an ALE description for FSI simulations with an isogeometric finite element method applied to blood flow and wind turbines. Space-time finite elements permit more flexibility with regards to moving the fluid mesh, and they have been studied extensively by Tezduyar et al. [56] -[63] . Their deforming-spatial-domain/stabilized space-time DSD/SST formulations combined with space-time interface projection techniques have been used to solve problems ranging from parachute dynamics to arterial fluid mechanics.
Our overset grid approach to FSI problems shares similarities with both ALE and EL approaches. We utilize a fixed Eulerian background mesh for our fluid domain as in EL methods. We compute the structural solution on the fixed Lagrangian mesh. The fluid flow on the moving, boundary-conforming composite meshes is computed in the ALE frame. Solution coupling between the fluid and solid regions is done via the ALE approach; however, the flow coupling between the fixed background mesh and the composite meshes surrounding the solids is handled through the use of overset interpolation operators, which is somewhat analogous to the use of the coupling schemes that EL methods use to couple the Eulerian and Lagrangian frames. The difference is that in our method we implicitly couple the Eulerian and the ALE frames rather than the Eulerian and Lagrangian frames.
The overset grid method for fully-coupled FSI simulations has only previously been studied by Wall et al. [12] [64] . In their approach, each fluid grid used was solved sequentially; that is, the overset grid attached to a deformable body is solved separately from the background grid. Our overset method is similar in the hierarchy of grids used, but differs in that we build the overset grid interpolation directly into the algebraic system for the fluid region. As a result, we do not require any iterations over sequences of fluid grids, and we expect our method to provide a more efficient solution method. The main detriment of the Chimera approach in [12] [64] , as stated by the authors, is the fluid-fluid coupling procedure, where additional computational costs and interpolation errors for convection dominated flows.
Overset grid methods coupling flow fields to rigid solids or reduced order models of solids have been relatively popular in the computational fluid dynamics community. Small deformation transonic flutter using an overset, implicit aeroelastic solver were studied in [65] , where they used an algebraic mesh deformation technique for the grid motion. Prescribed helicopter rotor blade motion using first harmonics coupled to unsteady Navier-Stokes using overset was studied in [66] . [67] uses overset in a similar manner, coupling the flow field to a modal description of blade motion. Their work is unique in the choice of an algebraic algorithm for deforming the fluid grid. Overset is used for the pitch and heave of a surface combatant ship in large-scale DES computations in [68] . FSI using patched overset grids for rigid structural motion was accomplished in [69] . The use of overset grids for finite element methods (FEM) was explored in [70] [71] . Kato et al. [72] uses the overset FEM approach for LES, turbo-machinery and aeroacoustics with multiple dynamic frames of reference.
Our approach is similar to [65] in the use of overset grids; however, we allow for arbitrarily large structural movement. Our formulation and implementation removes the need for element deletion/addition that is commonly used to accommodate large topological changes in moving mesh simulations (see, e.g., [73] ). Rather, only the interpolation stencils and weights change in the overset interpolation step. This feature allows our method to handle situations including free moving deformable objects, and the possibility of extending it to include contact is straightforward with available algorithms.
Another drawback of moving mesh ALE methods is the need to solve for “arbitrary” mesh geometry to accommodate the structural displacements. No physical equation governs the mesh motion, and the only driving parameter is the known displacements of the fluid-structure boundary. There have been numerous proposed methods on what equations will yield quasi-optimal mesh topology (see, e.g., [74] ). One important aspect when calculating the mesh motion is that the chosen equations are typically solved over the entire computational fluid domain. The result is a non-trivial computation that can contribute significantly to the overall computational cost of an FSI algorithm. Our overset FSI method circumvents the need for a “global” mesh motion solution; we simply solve for updated mesh positions on the composite grids that surround deformable bodies. This results in a greatly reduced computational load for the mesh motion, as only a subset of the grid positions are involved in the computation. Moreover, motion of the composite grids is generally simplified because they typically have no outer constraints, resulting in improved mesh quality.
The objective of the present work is to implement and demonstrate the advantages of coupling the overset mesh technology and an ALE, partitioned FSI solution algorithm. The governing equations, which are also outlined by Campbell and Paterson [75] but provided here for completeness, are described and the discretization approach is presented. We briefly overview the standard numerical methods used, and we provide a description of how the overset mesh method is implemented within our solvers. A sample numerical benchmark test case based on the work of Turek and Hron [3] is presented to demonstrate the improved mesh quality and solver performance.
2. Governing Equations
One of the main challenges for coupling fluid and solid domains arises from the “natural” mathematical descriptions of the physics. The governing equations for a fluid flow are cast in an Eulerian (spatial) description, while the equations for a solid are written in Lagrangian (referential) form. Aside from that, the balance laws governing the behavior of both the fluid and solid domains are identical. We introduce the general continuum mechanics balance laws in an arbitrary Lagrangian-Eulerian (ALE) frame which provides the framework to describe the Eulerian, Lagrangian, or an arbitrary frame of reference.
We first consider the balance of mass:
 (1)
(1)
where  is mass density,
is mass density,  is the (fluid or solid) particle velocity, and
is the (fluid or solid) particle velocity, and  is the velocity of the reference frame (the mesh velocity in an ALE method, which is required in this work to deform the fluid mesh to accommodate structural deformation). For a Lagrangian description,
is the velocity of the reference frame (the mesh velocity in an ALE method, which is required in this work to deform the fluid mesh to accommodate structural deformation). For a Lagrangian description,  , and for an Eulerian description on a stationary domain,
, and for an Eulerian description on a stationary domain, .
.
Performing a force balance and making use of the continuity equation leads to the momentum equation:
 (2)
(2)
where  is the Cauchy stress tensor and
is the Cauchy stress tensor and  is the body force per unit mass.
is the body force per unit mass.
An additional constraint for the ALE approach is that the mesh velocity satisfy the Geometric Conservation Law (GCL) [76] -[80] :
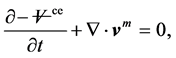 (3)
(3)
where 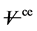 is the volume of a control element. The GCL requires the change in volume of each control element between two adjacent time steps equal the volume swept by the cell boundary during the time step. Farhat et al. [77] have shown that satisfying a discrete version of the GCL is a necessary and sufficient condition for a scheme to preserve the nonlinear stability of a scheme’s fixed grid counterpart.
is the volume of a control element. The GCL requires the change in volume of each control element between two adjacent time steps equal the volume swept by the cell boundary during the time step. Farhat et al. [77] have shown that satisfying a discrete version of the GCL is a necessary and sufficient condition for a scheme to preserve the nonlinear stability of a scheme’s fixed grid counterpart.
Equations (1) and (2) are referred to as the governing equations. Application of constitutive relationships provides the necessary closure of the governing equations. The constitutive relationships and resulting equations for the fluid and solid domains are provided next, followed by the procedure used to couple these domains at the fluid/solid interface  and details of the implementation.
and details of the implementation.
2.1. Fluid Equations in Eulerian Frame
We consider only incompressible Newtonian fluids in this work. The constitutive equation for the Cauchy stress tensor is
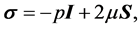 (4)
(4)
where  is the thermodynamic pressure,
is the thermodynamic pressure,  is the absolute viscosity, and
is the absolute viscosity, and  is the symmetric strain-rate tensor. The incompressibility constraint is written as
is the symmetric strain-rate tensor. The incompressibility constraint is written as
 (5)
(5)
Substitution of (4) into the momentum Equation (2) and utilizing (5) yields the Navier-Stokes equations:
 (6)
(6)
where  is the kinematic viscosity.
is the kinematic viscosity.
We deal with three types of boundary conditions for our simulations: inflow , outflow
, outflow , and solid wall
, and solid wall . Boundary conditions are specified as
. Boundary conditions are specified as
 (7)
(7)
 (8)
(8)
 (9)
(9)
Equations (5) and (6) will be solved for pressure and velocity using an ALE formulation in the present work. The ALE formulation is required to accommodate the structural deformations, thus imparting a non-trivial mesh velocity into the fluid region. We describe the numerical method used and its implementation in Section 3.1.
2.2. Solid Equations in Lagrangian Frame
The Lagrangian frame-of-reference specifies the material velocity is equal to the frame velocity . Balance of mass thus reduces to
. Balance of mass thus reduces to , which is independent of time. The momentum Equation (2) becomes
, which is independent of time. The momentum Equation (2) becomes
 (10)
(10)
where  are the material displacements
are the material displacements . The divergence of the first Piola-Kirchhoff stress with respect to material coordinates has been used in place of the spatial divergence of the Cauchy stress [81] .
. The divergence of the first Piola-Kirchhoff stress with respect to material coordinates has been used in place of the spatial divergence of the Cauchy stress [81] .
The numerical benchmarks published in Turek and Hron [3] use a St. Venant-Kirchhoff hyper elastic model, which we also use here. The second Piola-Kirchhoff stress tensor is
 (11)
(11)
where  are the Lamé parameters,
are the Lamé parameters,  is the identity tensor, and
is the identity tensor, and
 (12)
(12)
is the Green-Lagrange strain. The Piola-Kirchhoff stresses are related by , where
, where  is the deformation gradient.
is the deformation gradient.
Boundary conditions for (10) on the Dirichlet 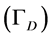 and Neumann
and Neumann  boundaries are specified as
boundaries are specified as
 (13)
(13)
 (14)
(14)
In this work, it happens that the Neumann partition of the boundary is coincident with the fluid-structure boundary .
.
2.3. Fluid-Structure Coupling
The fluid-structure interaction is accomplished by imposing fluid stresses on the solid (i.e., the tractions in (14)) and imparting the solid displacements and velocities to the fluid. The requirements for compatibility and the no-slip condition require the following:
 (15)
(15)
where  is the unit normal on the interface in the spatial configuration and the superscripts on the Cauchy stress
is the unit normal on the interface in the spatial configuration and the superscripts on the Cauchy stress  denote either the fluid or solid domain.
denote either the fluid or solid domain.
2.4. Mesh Motion
Our FSI approach requires changes to the spatial discretization (“mesh”) to accommodate the structural displacements in the fluid domain. The solution of the governing equations for the solid provides the interfacial displacement; however, there is no physical specification of the manner in which the mesh should deform away from the interface. The only requirement is that the mesh points on  move with the interface. Additionally, it is the time derivative of the mesh displacement that enters the fluid’s governing equations as the mesh velocity
move with the interface. Additionally, it is the time derivative of the mesh displacement that enters the fluid’s governing equations as the mesh velocity .
.
There have been numerous methods proposed to solve for the mesh motion; see the reviews in [74] [82] . We employ two methods in our work: 1) diffusion of the interface displacements into the mesh using the Laplace equation:
 (16)
(16)
where  is the mesh displacement from the original position and
is the mesh displacement from the original position and  is a variable diffusion coefficient, and 2) a linear-elastic solid analogy that requires the divergence of Cauchy stress be zero everywhere:
is a variable diffusion coefficient, and 2) a linear-elastic solid analogy that requires the divergence of Cauchy stress be zero everywhere:
 (17)
(17)
Equation (17) is similar to Equation (10) for the solid, but without the inertial or body force terms and with Cauchy stress instead of the first Piola-Kirchhoff stress. The mesh is represented by a linear-elastic solid
 (18)
(18)
and uses a small-strain approximation
 (19)
(19)
In either choice, the mesh motion equation governs the fluid mesh position, and the fluid solver approximates the mesh velocity based on the solution time step and the mesh displacement. For instances where the interface motion is a small fraction of the smallest characteristic length of the interface cells, only the boundary points of the fluid mesh are moved and the remainder of the mesh remains stationary.
3. Numerical Method
Commercial software packages for Computer Aided Engineering (CAE) have recently been developing “multiphysics” capabilities, one of which is FSI. Most, if not all, of the available packages implement an ALE approach. The ADINA System [83] supports FSI calculations in a monolithic solution framework based solely on finite elements. Comsol Multiphysics [84] offers a similar finite element-based monolithic FSI solver. The Star-CCM+ software suite by CD-Adapco [85] offers an overset capability for finite volume-based CFD simulations, with the possibility of implicitly coupling rigid structural motions with a six degree-of-freedom solver. They also offer a deformable solid FSI solution procedure by coupling to the commercial finite element package ABAQUS [86] ; however, the overset and deformable solid FSI capabilities can not yet be combined into an overset FSI method. While these commercial softwares are able to solve a small subset of FSI problems, they represent “black boxes” that cannot be user-modified to achieve our current goals. Thus, we have developed our overset FSI method through the use of open-source and in-house software tools.
We utilize a finite volume method (FVM) for the fluid equations and a finite element method (FEM) for the solid equations. The overset capability is added through the use of the foamed Over library [87] . The need to communicate solution information between solvers, preferably in memory and without the need for file I/O operations, has resulted in the use of an open-source flow solver and an in-house structural solver. Additionally, we need to be able to couple the flow solver to our overset grid tools (described in Section 3.4). These requirements have resulted in a customized FSI solver that will be expanded to larger and more challenging problems in the future.
3.1. Finite Volume Method for the Fluid Region
The governing fluid mechanics equations are solved using the open source software OpenFOAM [88] -[91] . OpenFOAM is the flow solver of choice for this effort because it facilitates custom integration with third-party solvers, has a pre-existing mesh motion capability that satisfies the GCL, and its source code is freely available through the GNU General Public License. OpenFOAM is an object-oriented library for numerical simulations in continuum mechanics, written in the C++ language. OpenFOAM offers co-located, cell-centered finite volume numerics of second order accuracy for a variety of continuum physics. It offers a segregated solution procedure, whereby each equation is solved independently and sequentially. OpenFOAM version 2.1.x has been used for our implementation.
The flow problems considered herein are transient and incompressible, and on moving meshes; therefore OpenFOAM’s icoDyMFoam solver provides a baseline for development. The only modifications necessary for our overset-FSI method were adding the overset grid capability (see Section 3.4 for details). The icoDyMFoam solver uses the PISO (Pressure Implicit Splitting of Operators) [92] [93] algorithm to solve for the pressure and velocity fields. The general idea is to use the momentum equation to advance the velocity solution in time, and then a pressure-Poisson equation is derived such that the pressure solution enforces the incompressibility constraint in a Lagrange-multiplier fashion.
3.2. Finite Element Method for the Solid Region
The structural mechanics governing equations are solved using the finite element approach, implemented in an author-written C++ program called feanl (finite element analysis non-linear). The governing Equation (10) is discretized via a Bubnov-Galerkin weighted residual method to obtain the weak form [94] -[97] ; as such, details will be omitted here. The application of Dirichlet boundary conditions (13) occurs by elimination of equations from the governing system of equations that result after discretization of the structural domain and application of the finite element method. The geometric-nonlinearity present due to the Green-Lagrange strain is handled with a Newton-Raphson solution scheme.
3.3. Mesh Motion
The governing mesh motion equations are solved using either OpenFOAM or feanl, depending on the type of mesh motion chosen at run time. Both approaches require a Dirichlet condition on the fluid/solid interface and the fluid mesh motions are computed. The Laplace mesh motion, represented by (16), uses a finite volume approach within OpenFOAM to determine mesh deformation. Either a constant or a variable diffusivity is chosen and mesh motion is computed based on the motion of the interface vertices. Equation (16) is discretized using the fluid mesh and thus the mesh motion solution requires a separate equation solution but does not require a separate mesh.
The linear-elastic solid analogy, described by Equations (17)-(19), employs a finite element approach and is solved using feanl. This approach requires a finite element mesh that overlays the fluid mesh in the moving region, which can be the entire fluid domain, or a subset of the domain. This mesh in general is substantially coarser than the fluid mesh, and is limited only by 1) maintaining sufficient resolution at the fluid-solid interface to preserve the physical boundary, and by 2) producing sufficient quality of the morphed fluid mesh. An interpolation scheme is employed within the finite element solver to prescibe motion of all fluid verticies that fall within the elements. The ability to employ a vastly coarser mesh reduces solution times. All aspects of the general-purpose finite element solver are applicable to the mesh motion solver, including variation of material properties to mimmic the variable diffusivity option of the Laplace mesh motion approach.
3.4. Overset Grid Method
In the present study, the grid deformation that results from solving the coupled fluid-structure interaction is facilitated through the use of overset grids. The capability in this case is provided by an overset grid library named foamedOver that was previously added to OpenFOAM by one of the current authors (Boger) [87] . FoamedOver itself is essentially a bridge between OpenFOAM and several other software packages, including DiRTlib [1] , Suggar++ [1] [2] [98] -[101] , and PETSc [102] . DiRTlib simplifies the addition of the overset capability to an existing flow solver by encapsulating commonly needed operations, such as the gathering and scattering of the flow data at the interpolation locations [1] . Suggar++ provides the overset assembly or domain connectivity information, which includes designation of out cells (hole cutting) and fringe cells as well as the determination of the interpolation stencils and weights [2] . Other packages such as Pegasus [103] provide similar capability, but Suggar++ is particularly suited for the present case since it has native capability for dynamic and/or deforming cell-centered unstructured grids. Finally, PETSc is a suite of data structures and routines for the parallel solution of large systems of linear and non-linear equations [102] . In this case, PETSc was used to facilitate the construction and solution of the linear systems of equations, which were modified to account implicitly for the intergrid boundary conditions. So for example, the pressure equation is normally solved using the default preconditioned GMRES solver in PETSc. The momentum equations, on the other hand, are normally solved using a weighted Jacobi scheme [104] .
Several hole-cutting methods and interpolation schemes are available in Suggar++. The domain connectivity information for the cases presented here result from an octree-based hole cutting method and use a least-squares method for interpolation.
3.5. Fully Coupled, Partitioned FSI Algorithm
We employ the partitioned FSI approach of Campbell et al. [75] in this work. In particular, we utilize an identical partitioned iteration procedure, relaxation, and convergence checks. We shall summarize here for completeness.
Figure 1 shows the solution algorithm for our tightly coupled partitioned FSI method using a fixed-point iteration. The fixed-point iteration uses (Aitken’s) under-relaxation to control the structural displacements passed to the fluid, thereby improving robustness and accelerating convergence. The fluid solver (OpenFOAM) passes force information to the solid solver (feanl), which in turn passes the interfacial displacements to the fluid mesh solver. When overset meshes are used, the domain connectivity information (DCI) must be updated every time the mesh is moved.
4. Numerical Results
We present numerical results for a single FSI validation problem defined by Turek and Hron [3] . We do so in the context of comparing different strategies for the mesh motion component of the simulation. In particular, we compare a non-overset FSI method with several variants of our overset mesh FSI method and demonstrate improved mesh quality and performance during the simulations.

Figure 1. Partitioned approach to FSI showing a fixed-point iteration with under-relaxation for tightly coupled solutions.
4.1. Types of Mesh Motion
The results presented herein demonstrate the behavior of three distinct mesh motion assemblies, as listed below. The name in bold type is used from this point forward to reference a mesh motion scheme.
1. Non-overset: A single body-fitted fluid mesh which is deformed throughout the entire fluid domain. This is the legacy approach.
2. Full Overset: A body-fitted overset mesh assembly where the motion of the entire assembly is computed over the entire fluid domain. This is the naive implementation of overset mesh technology into the existing algorithm.
3. Subset Overset: A body-fitted overset mesh assembly where the background mesh is assumed static and only the motion of the overset grid components attached to the deformable structure is computed.
In all of the above cases, the mesh motion displacement is computed by solving a vector-valued Laplace equation with boundary conditions prescribed by the exterior of the fluid domain and the deformation of the solid structure. As described in Section 3.3, we have implemented an additional solver option that can be used with any of the aforementioned mesh assemblies. Therefore, the two mesh motion solver options are:
1. Standard isotropic vector Laplace equation solver with variable diffusivity.
2. An overlay solver (described in Section 3.3) that uses an auxiliary finite element mesh that overlays the moving fluid region and is solved using feanl; variable mesh stiffness is accomplished through mesh property variation.
4.2. Benchmark Problem of Turek and Hron
The reference test case proposed by Turek and Hron [3] was selected to benchmark and validate the proposed overset grid FSI solver presented in this work. The case was developed as an improvement on Ramm and Wall’s test case from 1998 [105] , in order to compare the speed and accuracy of newly developed FSI codes, schemes, and approaches. Goals of the reference case were reproducible dynamic steady state solutions and the generation and presentation of this solution data. The resulting two-dimensional case consists of a slightly off-center cylinder immersed in channel flow, with a flexible trailing structure, as shown in Figure 2. The flow over the cylinder sheds vortices which then impinge on the flexible tail and cause it to oscillate. Details of domain dimensions are included in Table 1, and the ramped parabolic inlet velocity is defined by Equations (20) and

Table 1 . Dimensions of the Turek benchmark test case [3] .

Figure 2. Diagram of the Turek and Hron FSI benchmark test case geometry [3] .
(21). Physical constants, such as fluid velocity and material properties, were chosen to support simple periodic oscillations of the tail. We will compare our calculations with those of Turek and Hron [3] in their “FSI2” case, which uses the physical properties included in Table2
 (20)
(20)
 (21)
(21)
4.3. Mesh Generation and Validation
The implementation of an overset grid FSI case requires the generation of three separate mesh components: the background fluid mesh, the dynamic overset fluid mesh attached to the deformable structure, and the solid mesh, as seen in Figure 3. The background fluid mesh spans the entire domain, while the overset fluid and solid domains are specific to the immersed geometry being modeled. The interpolation between the background and

Figure 3. Decomposition of Overset FSI meshes: static background (gray), dynamic overset (blue), solid (red). Note the disparate number of cells between the solid and fluid meshes along the fluid-structure interface. The lower images demonstrate the ease with which the solid geometry can be changed.

Table 2. Physical Properties of the Turek benchmark test case [3] .
overset fluid meshes is performed by Suggar++, as described in Section 3.4. The result of the overset approach is a solver with the ability to easily add and modify solid features in a given fluid domain, as illustrated by Figure 3. Note that the nodes of the cells in the solid and overset fluid meshes do not need to be coincidental on the fluid-structure interface. This feature arises naturally from the partitioned nature of this FSI algorithm, and allows for different meshing requirements to be met for each constituent part of the domain.
Before delving into the formal study, we present in Figure 4 a sample calculation of the motion of the flexible tail and the flow field during several time steps of our simulation of the FSI2 case by Turek and Hron [3] . The interaction between the shed vortices propagating down the channel, from left to right, and the flexible tail’s deformation is easily observed. We also note that the deformation of the tail is not amplified in these images, demonstrating that we are in fact simulating a case with large solid deformations that subsequently interact with the flow field. The solution is not stationary but does eventually reach a steady state.
To address the issue of verification and validation, we extract from our simulations the displacement of the vertical midpoint of the the trailing end of the flexible tail and compare it to the values reported by Turek and Hron [3] . The position of this measurement is denoted by a black dot on the tip of the tail in Figure 2.
In Figure 5 we show two results. The left image shows the tip displacement components over a scaled time period of two steady state oscillations, for all three of our mesh assembly approaches. The values presented were calculated with all numerical schemes and tolerances held constant, except for the method of grid assembly and mesh motion. We have confirmed that all three methods of grid assembly produce the same tip displacements.
The right image in Figure 5 is a comparison of our calculated horizontal displacements with those from the Turek and Hron [3] FSI2 case. With our initial coarse mesh, we obtain values within a few percent of the reported results, and after appropriately refining the fluid and solid meshes our results agree very well with the previously reported values. Because we have verified that all three approaches match each other, and that refining the mesh brings the solution as close to the Turek and Hron data as we desire, we feel comfortable that our algorithms are implemented correctly and functioning as designed.
4.4. Mesh Motion Comparison Study
This section contains the primary result of this research effort, namely the demonstration of significant improvement in mesh quality during large deformation FSI simulations via the implementation of overset grid methods. We compare three reproductions of the FSI2 test case in this section: the legacy non-overset mesh approach, the overset mesh approach, and the overset mesh approach with the overlay mesh motion solver. We note that there is no difference in the solution between the full and subset overset techniques, and as such we only report results of the subset overset approach here.
Figure 6 shows the results of running the FSI2 Turek case with each of the aforementioned mesh assembly approaches. We see many differences in the resulting meshes at a given time step of maximum deflection. Most

Figure 4. Still images of our reproduction of the FSI2 case from Turek and Hron [3] , starting at the upper left and moving right then down and left and so on. The grey scale represents velocity magnitude, with contours showing regions of equal value.

Figure 5. Verification of the overset FSI algorithms. We compare the calculated tip displacement between all three mesh assembly approaches (left) and our calculated displacements to those from Turek and Hron [3] (right). All of the approaches produce the same results and match the previously reported results.
notably, cell deformations are distributed through the domain in the non-overset case. This leads to stretched cells at the top of the channel and compressed cells at the bottom. Concerns in cell skewness and aspect ratio occur in regions that would be important for boundary layers in this case, but in general the motion of the mesh in the entire domain is undesirable for preserving accuracy. However, in the overset case, background mesh quality is maintained due to the fact that the overset mesh is moved independently. This leads to a predictable background mesh in FSI problems, which is important for preserving mesh quality in areas of importance away from the fluid-structure interface.
In the overset fluid mesh (middle, Figure 6), cell deformation at the tip of the tail is similar to the non-overset case due to the use of the same standard mesh motion solver for both cases. This is seen more clearly in Figure 7, which shows a zoomed-in region around the deformed overset and non-overset meshes at the tip of the tail. Despite this, it is noted in the overset case that all poor quality cells are confined to the overset mesh.
One way to resolve this involves stiffening the mesh around the tail, which results in the mesh remaining tangent to the tip of the tail. This is precisely what is done in the overlay mesh motion solver. As shown in the

Figure 6. Comparison of mesh motion strategies: the legacy non-overset approach (top), the overset approach with the same mesh motion solver as the legacy approach (middle), and the overset approach with the overlay mesh motion solver (bottom). While all three approaches find the same deflection, the mesh quality clearly improves from top to bottom. The introduction of overset mitigates much of the mesh distortion throughout the domain, and the improved non-uniform stiffness mesh motion solver greatly improves the mesh quality in the deformed overset mesh.
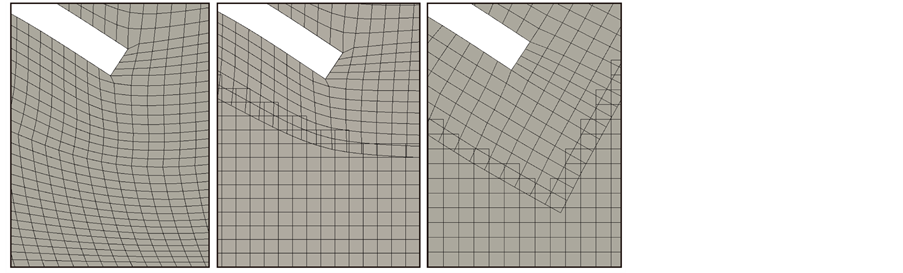
Figure 7. Zoomed view of the fluid mesh surrounding the tail in Figure 6. The non-overset case (left) and overset case (middle) show similar mesh distortion at the tip of the tail, as is expected since they were computed with the same standard mesh motion solver. The overset case with the non-uniform stiffness overlay mesh motion solver (right) corrects this issue and creates a large displacement mesh with very good cell quality.
bottom image of Figure 6 and in Figure 7, this results in a much better quality mesh at the tip of the tail, effectively maintaining the original quality of the entire mesh. In addition, it can be noted that with this improvement in cell quality, there was also an improvement in overset communication, leading to a shorter trailing mesh.
In summary, all of the mesh assembly methods we have proposed are capable of reproducing the results in the FSI2 case from Turek and Hron [3] . The use of overset mesh assemblies improves the mesh quality away from the fluid-structure interface by maintaining a static background mesh, but it does not alleviate the issue of mesh distortion near the interface. We demonstrate that overset meshing combined with a non-uniform stiffness overlay mesh motion solver can preserve mesh quality even during large deformation simulations.
4.5. Timing and Performance Improvements
In the previous section, we address and demonstrate the improvement in mesh quality during large deformation simulations that is enabled via overset mesh techniques. In the present section we explore the computational cost of this added capability. To do so, we track the time required to run the FSI2 case from the Turek and Hron [3] study for the three mesh assembly approaches given in Section 4.1.
Figure 8 shows the average wall-time per timestep that was needed by the solver to compute the mesh motion component of the FSI algorithm. The average wall-time is the wall-time for the entire timestep divided by the number of FSI subiterations during that timestep. As we can see, the naive implementation of the overset mesh technology into the legacy solver, where the motions of all points in the grid assembly are calculated, increases the run time of the algorithm. However, when we consider the background mesh of the overset grad assembly to be fixed, and calculate the motion of only the grid components attached to the flexible interface, then we see a substantial reduction in the mesh motion solver time as compared to both the full overset and non-overset cases.
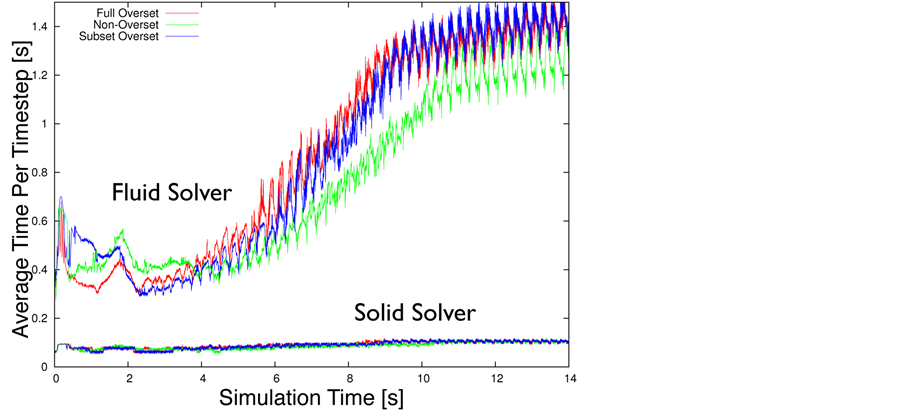
In order to judge the net effect of reducing the mesh motion solver time on the entire simulation time, we include in Figure 9 the average wall-time per timestep of the fluid and solid solver (top) and average wall-time per timestep of the entire FSI algorithm (bottom). The results in this figure, for this example problem, clearly show the wall time for the solid solver is less then the mesh motion solver, but that the fluid solver wall-time dominates the run time of the problem. However, there is a small overall reduction in the total run time by using the subset overset mesh motion approach.
This is an important observation, given that we have added functionality, i.e., improved mesh quality for large deformations, while retaining or reducing the run-time of the problem. This benefit is expected to be amplified for three dimensional domains, providing further advantage of the overset approach.

Figure 8. Average wall-time for mesh motion solution per timestep plotted as a function of simulation time. The naive addition of overset mesh technology into the solver increases the mesh motion wall-time, while the optimization for moving only the subset of the overset assembly attached to the deforming structure results in reduced walltime.
 (a)
(a) (b)
(b)
Figure 9. Average wall-time for the fluid and structural solutions per timestep (a) plotted as a function of simulation time, and the total solver average walltime (b). The fluid solver dominates the run-time of this problem, but the overball simulation time does not increase with the addition of the overset meshing technology.
5. Conclusions
We have developed and demonstrated an FSI simulation method based on the ALE formulation of the governing equations. Our partitioned algorithm allows for the modular introduction of separate, optimized fluid and structural solvers that are joined by a custom framework to pass information between them and perform the necessary mesh motion. The focus of this work is on the mesh motion component of the problem, as it is the source of many difficulties in FSI simulations where large deformation occurs.
To this end, we have proposed to use overset grid technology to alleviate some of the mesh motion difficulties. We have implemented overset technology into the FSI algorithm, verified it against the legacy mesh motion technique, and validated it against previously published computational results. When only the motions of the overset mesh components attached to the deforming immersed structure are calculated, we are able to simultaneously preserve mesh quality without expensive re-meshing, but also fundamentally maintain or reduce the runtime of the algorithm. A key component of this achievement is the use of the non-uniform stiffness overlay solver to compute the mesh motion in a manner that optimizes deformation of the mesh away from the fluidstructure interface.
While the authors are excited about the results contained in this work, we are also optimistic that when this algorithm is applied to more complex geometries and three dimensional domains, where mesh motion can be a large fraction of the computation time, we will see an even more pronounced improvement in mesh quality and performance. We plan to extend this solver and apply it to three dimensional RANS simulations in the near future.
Acknowledgements
The authors would like to acknowledge support for this research from the Applied Research Laboratory at The Pennsylvania State University, especially the student support from the ARL Undergraduate Honors Program.
NOTES
*Corresponding author.

1We shall omit the multitude of steady-state as well as partially (or “loosely”) coupled FSI methods in our brief review, except in the case that overset grid methods are utilized.