Semimicroscopic Dispersive Analysis of Nuclear-Nuclear Collisions on the Basis of Folding Potential ()
Figure 1. Ratios of the differential cross sections for elastic scattering α + 12C system.
Figure 2. Positions of the Airy minima for α + 12C system.
Figure 3. Dispersion analysis of volume integrals of dispersive potentials for the α + 12C system.
liding nuclei, third test, has been shown in Figure 4. In this figure, the stars showed in the energies (center of mass) of 80 and 120 MeV in first Airy minima are the results that, clearly, are satisfactory.
The farside components calculated by us have been shown in Figure 5. As we expected, the Airy minima shifts toward small degrees with increasing energy of projectile. The radial dependence of the calculated total real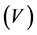 
and the total imaginary 
parts of the potentials at various laboratory energies have been shown in Figure 6.
3. Conclusions
A semimicroscopic analysis of a set of experimental data of elastic 
scattering was performed at several
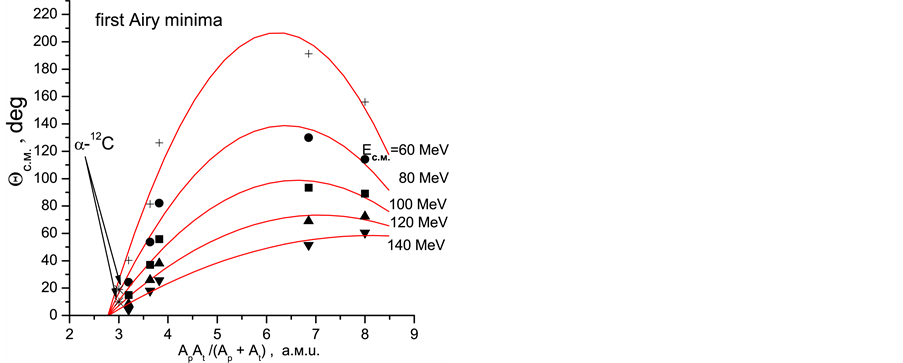
Figure 4. Estimated positions and approximating secondorder polynomials curves of first Airy minima versus the reduced mass.
Figure 5. Calculated farsaid components for α + 12C system.
Figure 6. Found radial dependence of the total real and imaginary part of potential for α + 12C system at various laboratory energies.
laboratory energies. In this way, the microscopic calculation of static component of potential combines with the phenomenological calculation of the dynamical component of potential. In this model, the dynamical polarization potential is constructed on the basis of physically justified combinations of the volume and surface forms whose geometric parameters are assumed to be independent of energy.
The energy systematics of the positions of Airy minima was constructed, and it was shown that their positions depend linearly on the inverse center of mass energy. The energy dependence of the volume integrals was performed and has been shown that the dispersion relation is satisfied and agrees well with the results obtained within a phenomenological analysis. Using systematics of the positions of Airy minima with respect to reduced mass of colliding nuclei introduced by Goncharov and Izadpanah, has been shown that the found positions of the Airy minima satisfy the rule of the quadratical dependence of the position of the Airy minima on the reduced mass of colliding nuclei.
Using these three systematics, the parameters of the model potential at various energies have been determined unambiguously.
The obtained imaginary components are shown the meaningness of aberrations from its Woods-Saxon forms obtained using the phenomenological approach. This aberration occurs in the distances about 1 fm and one can be due to ignore of the dependence energy in this study.
Acknowledgments
We are grateful to C.А. Goncharov for enlightening comments and discussions.