1. Introduction
The subject of this short note stems from a classroom exercise. I proposed my students to evaluate the effect on the degenerate levels of the hydrogen atom of a perturbation with potential energy
. At the first order in perturbation theory this problem requires the diagonalization of the matrix representing the perturbation restricted to the 
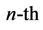degenerate subspace (see Appendix A).
(1)
The problem in itself appears to involve a rather standard (and boring) calculation based on the properties of Laguerre and Legendre functions. To save time one can attack the problem using a computer algebra system, like Mathematica1 and the matrix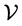 
can be readily constructed; if we are lucky enough, its spectrum could be exhibited in closed form or at least in numerical terms. Now, the surprise is that the eigenvalues turn out to be all simple rationals of the form 
where m runs from 
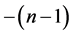to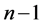 
and they are 
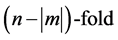degenerate. The result is so simple that one cannot be satisfied by the brute-force calculation, and he or she is forced to look for some explanation. Obviously the first idea that comes to mind is that this result should rely on some Lie-algebraic property. In the following I’m going to explain how hydrogen’s 
symmetry accounts for the result.
2. Dipole Operators and the SO(4) Generators
The origin of the Lie-theoretic explanation lies in one of the first papers about quantum mechanics [1] . In the book by Gottfried and Yan [2] 2 one can find all details in a masterly presentation. In this note, however, we present a somewhat simpler derivation, suitable for an introductory Quantum Mechanics course. In particular we give a simple derivation of Pauli’s link between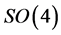 
Casimir operator and the Hamiltonian, which cannot be found in most textbooks (see Appendix B). Other relevant information is contained in the recent paper [3] with generalization to higher multipoles.
The fact is: hydrogen atom, in its simplest terms, described by the Hamiltonian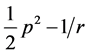
, exhibits a larger degeneracy than required by rotational invariance, the 
level being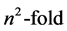 
degenerate. This fact was related, since Pauli’s paper, to the presence of an extra conserved vector quantity, which in classical mechanics is known as the Laplace-Runge-Lenz vector and was used by Pauli in the calculation of the spectrum. This should be considered as the first example of dynamical symmetry in Quantum Mechanics. The quantum conserved vector is
(2)
where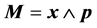 
and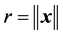
. Since 
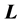commutes with the Hamiltonian it can be normalized by adding a factor 
in such a way that 
and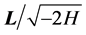 
close the Lie algebra of 
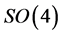under commutation. In his 1926 paper Pauli showed that this fact was sufficient to derive Balmer’s formula and the “dipole matrix elements” 
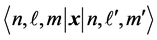in terms of the matrix of 
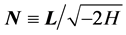in the same 
degenerate subspace. Denoting by 
the orthogonal projector on the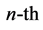 
degenerate subspace, it is immediately realized that
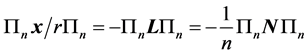; no contributions arise from the term 
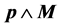which has vanishing matrix elements between degenerate states since it coincides with the commutator
. Now, since N belongs to the Lie algebra of the symmetry group
, its spectrum is fixed by group theory alone. Simply enough,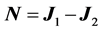 
where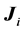 
are the generators of the two 
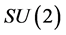factors of
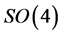. Since 
and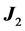 
commute, and the total angular momentum is 
for each of them, the spectrum is simply given by 
that is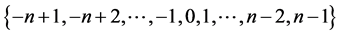 
with degeneracy
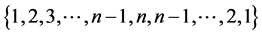. As a result the spectrum of the matrix 
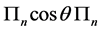is precisely given, as anticipated, by
(3)
For the sake of completeness we recall the detailed expression for the eigenfunctions and the matrix elements in appendix.
3. Conclusion
It is clear that the use of a symbolic algebra system can easily give the spectrum of the dipole x or, more generally,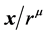
. For instance one can check immediately that the matrix identically vanishes for
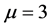, the case of the electric dipole perturbation. However the connection with group theory gives a deeper insight into the result, which by itself could remain a simple mathematical curiosity. Let us notice that in the classical book [4] by Condon and Shortley the calculations of the Stark effect perturbative corrections to the Balmer energies are beautifully obtained using parabolic coordinates, but the result of Equation (3) takes on a new light when interpreted group-theoretically.
Acknowledgements
This paper has a mere didactic interest and it is related to my thesis of 1968. It is my pleasure to thank Prof. Massimo Pauri, then my advisor and today Professor Emeritus at our Department, who taught me quite a lot about symmetry and group theory in Quantum Mechanics.
Appendix A
We adopt the convention for the hydrogen eigenfunctions as follows:
The non-vanishing matrix elements for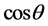 
are explicitly given by
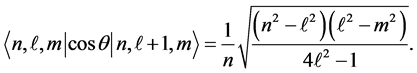
Appendix B
We prove the relation
(4)
In classical mechanics it holds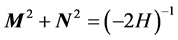 
which clearly cannot hold in quantum mechanics, since the left hand side annihilates the ground state. Quantum commutators provide the 
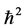shift which fixes the ground state. This was emphasized by Pauli in [1] . Now to the proof: since the action of 
spans the whole energy level and the identity links together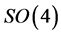 
invariants, we can limit ourselves to check the validity of Equation (4) to 
states. So we may reduce the proof to the more tractable identity
or, by defining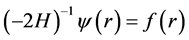
, we are left to prove
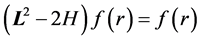(5)
Now, on s-states the definition of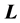 
gives
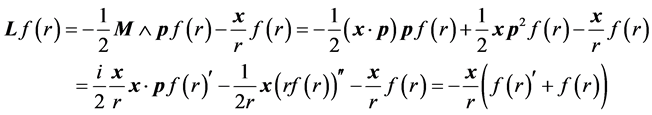
For instance 
annihilates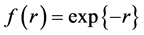
, 
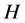has the value 
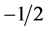and the relation is satisfied. Now in general, instead of evaluating 
it’s easier to check Equation (5) on the quadratic form
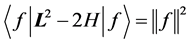
Indeed,
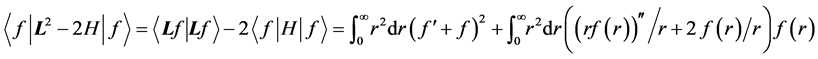
NOTES
1©Wolfram Research.
2I am indebted to Prof. G. Cicuta for attracting my attention to this reference.