Uniform Exponential Attractors for Non-Autonomous Strongly Damped Wave Equations ()
1. Introduction
In this paper, we study the following non-autonomous strongly damped wave equation on a bounded domain 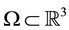 with smooth boundary
with smooth boundary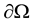 :
:
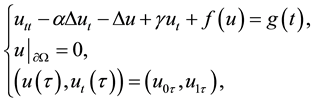 (1.1)
(1.1)
where 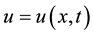 is a real-valued function on
is a real-valued function on 
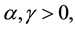
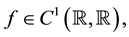

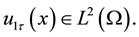 Let
Let 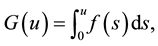 we make the following assumptions on functions
we make the following assumptions on functions 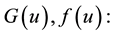
 (1.2)
(1.2)
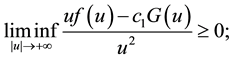 (1.3)
(1.3)
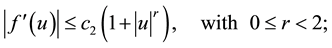 (1.4)
(1.4)
where 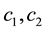 are positive constants. And we assume that the external force
are positive constants. And we assume that the external force 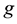 belongs to the space
belongs to the space ![]() and satisfies
and satisfies
![]() (1.5)
(1.5)
for some given (possibly large) constant![]() .
.
Wave equations, describing a great variety of wave phenomena, occur in the extensive applications of mathe- matical physics. Equation (1.1) can be regarded as a perturbed equation of a continuous Josephson junction where![]() , see [1] . There is a large literature on the asymptotic behavior of solutions for strongly damped wave equations (see, for instance, [1] - [9] ). In [9] , the author showed the uniform boundedness of the global attractor for large strongly damping and obtained an estimate of the upper bound of the Hausdorff dimen- sion of an attractor for strongly damped wave Equation (1.1) when
, see [1] . There is a large literature on the asymptotic behavior of solutions for strongly damped wave equations (see, for instance, [1] - [9] ). In [9] , the author showed the uniform boundedness of the global attractor for large strongly damping and obtained an estimate of the upper bound of the Hausdorff dimen- sion of an attractor for strongly damped wave Equation (1.1) when ![]() is independent of
is independent of![]() . But when the equations depend explicitly on
. But when the equations depend explicitly on![]() , the case can be complex.
, the case can be complex.
Recently, motivated by [6] , the authors have given a new explicit algorithm allowing to construct the expo- nential attractor, and this method makes it possible to consider more general processes in applications [10] [11] .
An exponential attractor ![]() is a compact semi-invariant set of the phase space whose fractal dimension is finite and which attracts exponentially the images of the bounded subsets of the phase space
is a compact semi-invariant set of the phase space whose fractal dimension is finite and which attracts exponentially the images of the bounded subsets of the phase space![]() . In non-autono- mous dynamical systems, instead of a semigroup, we have a so-called (dynamical) process
. In non-autono- mous dynamical systems, instead of a semigroup, we have a so-called (dynamical) process ![]() depending on two parameters
depending on two parameters ![]() (or
(or ![]() for discrete times). The asymptotic behavior of non-autonomous dy- namical systems is essentially less understood and, to the best of our knowledge, the finite-dimensionality of the limit dynamics was established only for some special (e.g. quasiperiodic) dependence of the external forces on time. Indeed, there exists, at the present time, one of the different approaches for extending the concept of a glo- bal attractor to the non-autonomous case which is based on the embedding of the non-autonomous dynamical system into a larger autonomous one by using the skew-product flow. This approach naturally leads to the so- called uniform attractor
for discrete times). The asymptotic behavior of non-autonomous dy- namical systems is essentially less understood and, to the best of our knowledge, the finite-dimensionality of the limit dynamics was established only for some special (e.g. quasiperiodic) dependence of the external forces on time. Indeed, there exists, at the present time, one of the different approaches for extending the concept of a glo- bal attractor to the non-autonomous case which is based on the embedding of the non-autonomous dynamical system into a larger autonomous one by using the skew-product flow. This approach naturally leads to the so- called uniform attractor ![]() which remains time-independent in spite of the fact that the dynamical system now depends explicitly on the time, see [12] . We note that however the uniform attractor reduces to an autono- mous system via the skew-product flow. It seems natural to generalize the concept of an exponential attractor to the non-autonomous case, see [11] [13] [14] . But in all these articles, the uniform attractor’s approach was used in order to construct an exponential attractor for the non-autonomous system considered and, consequently, an (uniform) exponential attractor remained time-independent. Since, under this approach, an exponential attractor should contain the uniform attractor, all the drawbacks of uniform attractors (artificial infinite-dimensionality and high dynamical complexity) described above are preserved for exponential attractors.
which remains time-independent in spite of the fact that the dynamical system now depends explicitly on the time, see [12] . We note that however the uniform attractor reduces to an autono- mous system via the skew-product flow. It seems natural to generalize the concept of an exponential attractor to the non-autonomous case, see [11] [13] [14] . But in all these articles, the uniform attractor’s approach was used in order to construct an exponential attractor for the non-autonomous system considered and, consequently, an (uniform) exponential attractor remained time-independent. Since, under this approach, an exponential attractor should contain the uniform attractor, all the drawbacks of uniform attractors (artificial infinite-dimensionality and high dynamical complexity) described above are preserved for exponential attractors.
In the present article, we study exponential attractors of the system (1.1) based on the concept of a non-au- tonomous (pullback) attractor. Thus, in the approach, an exponential attractor is also time-dependent. To be more precise, a family ![]() of compact semi-invariant (i.e.,
of compact semi-invariant (i.e.,![]() ) sets of the dynami- cal process (1.1) is an (non-autonomous) exponential attractor if
) sets of the dynami- cal process (1.1) is an (non-autonomous) exponential attractor if
1) The fractal dimension of all the sets ![]() is finite and uniformly bounded with respect to
is finite and uniformly bounded with respect to ![]()
![]()
2) There exist a positive constant ![]() and a monotonic function
and a monotonic function ![]() such that, for every
such that, for every ![]() and every bounded subset
and every bounded subset ![]() of
of![]() ,
,
![]() (1.6)
(1.6)
We emphasize that the convergence in (1.6) is uniform with respect to ![]() and, consequently, under this approach, we indeed overcome the main drawback of global attractors [13] .
and, consequently, under this approach, we indeed overcome the main drawback of global attractors [13] .
This article is organized as follows. In Section 2, we first provide some basic settings and show the absorbing and continuous properties in proper function space about Equation (1.1). In Section 3 and Section 4, we prove the existence of the uniform attractor and exponential attractor of Equation (1.1), respectively. Finally, we prove the existence of infinite-dimensional exponential attractor, and compare it with the non-autonomous exponential attractor in Section 5.
2. Preliminaries
We will use the following notations as that in Pata and Squassina [15] . Let ![]() be the (strictly) positive operator on
be the (strictly) positive operator on ![]() defined by
defined by
![]() with domain
with domain ![]()
and consider the family of Hilbert spaces ![]() with the standard inner products and norms, respec- tively,
with the standard inner products and norms, respec- tively,
![]() and
and
Then we have
![]()
and the compact, dense injections
![]()
In particular, naming ![]() the first eigenvalue of
the first eigenvalue of![]() , we get the inequlities
, we get the inequlities
![]()
We recall the continuous embedding
![]()
and the interpolation results: given ![]() for any
for any![]() , there exists
, there exists ![]() such that
such that
![]()
and let
![]()
Equation (1.1) is equivalent to the following initial value problem in the Hilbert space E
![]() (2.1)
(2.1)
where ![]()
![]() and
and
![]()
It is well known (see, e.g., [3] , [9] ) that, under the above assumptions, Equation (2.1) possesses, for every ![]() and
and ![]() a unique (mild) solution
a unique (mild) solution ![]() Thus, Equation (1.1) defines a dynamical process
Thus, Equation (1.1) defines a dynamical process ![]() in the phase space
in the phase space ![]() by
by
![]() (2.2)
(2.2)
Define a new weighted inner product and norm in ![]() as
as
![]()
for any
![]()
where ![]() is chosen as
is chosen as
![]() (2.3)
(2.3)
Obviously, the norm ![]() in (2.3) is equivalent to the usual norm
in (2.3) is equivalent to the usual norm ![]() in
in![]() .
.
Let
![]()
where ![]() is chosen as
is chosen as
![]() (2.4)
(2.4)
and then the system (1.1) can be written as
![]() (2.5)
(2.5)
where
![]()
![]()
Lemma 2.1 For any ![]() we have
we have
![]()
where
![]() (2.6)
(2.6)
Proof. Since ![]() is dense in
is dense in![]() , and
, and![]() ; we only need to prove lemma 2.1 for any
; we only need to prove lemma 2.1 for any
![]()
![]()
By (2.4) and (2.6), elementary computation shows
![]()
The proof is completed. ,
Lemma 2.2 Let assumptions (1.2)-(1.5) be satisfied. For any initial data![]() , there exists a positive con- stant
, there exists a positive con- stant ![]() depending only on the coefficients of (1.3) and (2.4) and
depending only on the coefficients of (1.3) and (2.4) and ![]() such that the following dissipative esti- mate holds:
such that the following dissipative esti- mate holds:
![]()
where ![]() is a monotonic function and where the positive number
is a monotonic function and where the positive number ![]() depends also on
depends also on ![]() (but is indepen- dent of the concrete choice of
(but is indepen- dent of the concrete choice of![]() ).
).
Proof. Write ![]() Let
Let ![]() be the solution of the system (2.5) with the initial
be the solution of the system (2.5) with the initial
value ![]() Taking the inner product
Taking the inner product ![]() of (2.5) with
of (2.5) with![]() , we have
, we have
![]() (2.7)
(2.7)
By (1.2), (1.3) and Poincaré inequality, there exist two positive constants ![]() such that
such that
![]() (2.8)
(2.8)
![]() (2.9)
(2.9)
By (2.4) and (2.6), ![]() Let
Let ![]() By (2.8)-(2.9), we have
By (2.8)-(2.9), we have
![]() (2.10)
(2.10)
where ![]() By (2.7) and (2.10),
By (2.7) and (2.10),
![]()
By Gronwall’s inequality, we have an absorbing property:
![]()
This completes the proof. ,
Theorem 2.1 Given any ![]() and for the solutions of (2.5) with any two initial data
and for the solutions of (2.5) with any two initial data ![]() such that
such that![]() , we have the following Lipschitz continuity in E
, we have the following Lipschitz continuity in E
![]()
for some![]() .
.
The proof is similar to Theorem 2 in [15] . ,
Theorem 2.2 For the solutions of (2.5) with different external forces ![]() and
and ![]() satisfying (1.5) and with the initial data
satisfying (1.5) and with the initial data ![]() and
and![]() , the following contiuity holds:
, the following contiuity holds:
![]()
where ![]() and
and ![]() are independent of
are independent of ![]() and
and ![]()
The proof is similar to Lemma 4 in [5] .
3. Existence of the Uniform Attractor
The dissipativity property obtained in Lemma 2.2 yields the existence of an absorbing set for the process ![]() on
on![]() . In the following section, we assume that
. In the following section, we assume that ![]() holds, where
holds, where ![]() is specified in (3.11).
is specified in (3.11).
Theorem 3.1 The process ![]() possesses a uniform attractor
possesses a uniform attractor ![]() in
in ![]()
Proof. We consider ![]() such that
such that
![]() (3.1)
(3.1)
and we introduce the splitting ![]() where
where ![]() satisfies
satisfies
![]() (3.2)
(3.2)
![]() satisfies
satisfies
![]() (3.3)
(3.3)
and ![]() is the solution of
is the solution of
![]() (3.4)
(3.4)
We now define the families of maps ![]() and
and ![]() in
in ![]() where
where
![]()
First step: We prove that ![]() is bounded in
is bounded in ![]() that the solution of (2.5) is starting in bounded sets of initial data
that the solution of (2.5) is starting in bounded sets of initial data![]() . The system (3.2) can be written as
. The system (3.2) can be written as
![]() (3.5)
(3.5)
where![]() ,
,
![]() (3.6)
(3.6)
Similar to Lemma 2.1, we have
![]()
where ![]() is as (2.6). Multiply (3.5) by
is as (2.6). Multiply (3.5) by![]() , so we get
, so we get
![]() (3.7)
(3.7)
Similar to Lemma 2.2, applying (3.7) and Young, Poincaré, Gronwall inequalities, we obtain
![]()
Now we multiply (3.5) by ![]() and integrate over
and integrate over ![]() to obtain
to obtain
![]() (3.8)
(3.8)
with
![]()
Then from (3.8) we have
![]()
i.e.,
![]() (3.9)
(3.9)
for the first term on the right-hand side of (3.9), we have
![]() (3.10)
(3.10)
By (3.9), (3.10), and Lemma 2.2, there is ![]() such that for all
such that for all ![]()
![]() (3.11)
(3.11)
let ![]() using the Gronwall’s lemma, we have
using the Gronwall’s lemma, we have
![]() (3.12)
(3.12)
By (1.2), (1.3) and (2.8), (2.9), from (3.12), we obtain
![]() (3.13)
(3.13)
Lemma 2.2 and (3.13) imply that ![]() is bounded in
is bounded in![]() .
.
Second step: Let![]() , we will prove that there exists
, we will prove that there exists ![]() independence of
independence of ![]() such that
such that
![]()
Multiply (3.3) by![]() , we thus obtain
, we thus obtain
![]()
due to Gronwall and Poincaré inequalities, then
![]() (3.14)
(3.14)
Since the embedding ![]() is compact, (3.13), (3.14) and the following lemma imply that
is compact, (3.13), (3.14) and the following lemma imply that ![]() is compact in
is compact in![]() .
.
Lemma 3.1 (see [16] ) Let ![]() be a complete metric space and
be a complete metric space and ![]() be a subset in
be a subset in![]() , such that
, such that
![]()
with ![]() and
and ![]() is compact in
is compact in![]() , then
, then ![]() is compact in
is compact in![]() .
.
Third step: Let![]() , the same arguments in the Equation (3.4) lead to
, the same arguments in the Equation (3.4) lead to
![]() (3.15)
(3.15)
Then from (3.15), Lemma 2.2, and the compactness of![]() , the system (2.5) exists a uniform attractor
, the system (2.5) exists a uniform attractor ![]() in
in ![]()
It is easy to see that the process
![]()
defined by (2.5) has the following relation with![]() :
:
![]() (3.16)
(3.16)
where ![]() is an isomorphism of
is an isomorphism of ![]()
![]()
Since the process ![]() possesses a uniform attractor
possesses a uniform attractor ![]() by (3.16),
by (3.16), ![]() also possesses a uniform attractor
also possesses a uniform attractor ![]() ,
,
4. Existence of Exponential Attractors
The main result of this section is the following theorem.
Theorem 4.1 Let the function f and the external force g satisfy the above assumptions. Then, for every ex- ternal force g enjoying (1.5), there exists an exponential attractor ![]() of the dynamical process (1.1) which satisfies the following properties:
of the dynamical process (1.1) which satisfies the following properties:
1) The sets ![]() are semi-invariant with respect to
are semi-invariant with respect to ![]() and translation-invariant with respect to time-shifts:
and translation-invariant with respect to time-shifts:
![]() (4.1)
(4.1)
where ![]() and
and ![]() is the group of temporal shifts,
is the group of temporal shifts, ![]()
2) They satisfy a uniform exponential attraction property as follows: there exist a positive constant ![]() and a monotonic function
and a monotonic function ![]() (both depending only on
(both depending only on![]() ) such that, for every bounded subset
) such that, for every bounded subset ![]() of
of![]() , we have
, we have
![]() (4.2)
(4.2)
3) The sets ![]() are compact finite-dimensional subsets of
are compact finite-dimensional subsets of ![]()
![]() (4.3)
(4.3)
where the constant ![]() is independent of
is independent of ![]() and
and![]() .
.
4) The map ![]() is Hölder continuous in the following sense:
is Hölder continuous in the following sense:
![]() (4.4)
(4.4)
where the positive constants ![]() and
and ![]() are independent of
are independent of ![]() and
and![]() ,
, ![]() denotes the symme- tric Hausdorff distance. In particular, the function
denotes the symme- tric Hausdorff distance. In particular, the function ![]() is uniformly Hölder continuous in the Hausdorff metric:
is uniformly Hölder continuous in the Hausdorff metric:
![]() (4.5)
(4.5)
where ![]() and
and ![]() are also independent of
are also independent of ![]() and
and![]() .
.
Proof. Firstly, we construct a family of exponential attractors for the discrete dynamical processes associated with Equation (2.5). According to Lemma 2.2, it only remains to construct the required exponential attractors for initial data belonging to the ball
![]()
where ![]() is a sufficiently large number depending only on
is a sufficiently large number depending only on ![]() given in (1.5), is a uniform absorbing set for all the processes
given in (1.5), is a uniform absorbing set for all the processes ![]() generated by Equation (1.1). Moreover, from Theorem 2.1, Theorem 2.2 and Theo- rem 3.1, it follows Lipschitz continuity and smooth properties for the difference of two solutions
generated by Equation (1.1). Moreover, from Theorem 2.1, Theorem 2.2 and Theo- rem 3.1, it follows Lipschitz continuity and smooth properties for the difference of two solutions ![]() and
and![]() . Thus, by Theorem 2.1 in [13] , the family of discrete dynamical processes
. Thus, by Theorem 2.1 in [13] , the family of discrete dynamical processes ![]() possess exponential attractors
possess exponential attractors ![]() For obtain- ing exponential attractors of the family of dynamical processes
For obtain- ing exponential attractors of the family of dynamical processes![]() , we need the Hölder continuity of the processes
, we need the Hölder continuity of the processes ![]() with respect to the time, see the following lemma.
with respect to the time, see the following lemma.
Lemma 4.1 Let the above assumptions on Equation (1.1) hold. Then, for every ![]() we have
we have
![]() (4.6)
(4.6)
where the constant ![]() depends on
depends on![]() , and is independent of
, and is independent of ![]() Moreover, for every
Moreover, for every ![]() we also have
we also have
![]() (4.7)
(4.7)
where ![]() is a positive number and the positive constant
is a positive number and the positive constant ![]() depends on
depends on ![]() but is independent of
but is independent of ![]() and
and![]() .
.
Proof. Note that there is a ![]() such that
such that
![]()
and ![]() is uniformly bounded in
is uniformly bounded in ![]() and Lemma 2.2, which imply the Hölder continuity (4.6). In order to verify (4.7), we note that, due to (4.6) and Theorem 2.2, for every
and Lemma 2.2, which imply the Hölder continuity (4.6). In order to verify (4.7), we note that, due to (4.6) and Theorem 2.2, for every![]() , we have
, we have
![]()
where all the constants depend on![]() , but are independent of
, but are independent of ![]() and
and ![]() Using the previously mentioned interpolation inequality in Section 2 finishes the proofs of estimate (4.7). ,
Using the previously mentioned interpolation inequality in Section 2 finishes the proofs of estimate (4.7). ,
Now, we can define the exponential attractors for continuous time by the following formula
![]()
with respect to ![]() The proofs of the semi-invariance with respect to
The proofs of the semi-invariance with respect to ![]() and translation-invariance with respect to time-shifts is similar to [11] [13] . Estimate (4.2) follows in a standard way from Lemma 2.2, Theorem 3.1 for the processes
and translation-invariance with respect to time-shifts is similar to [11] [13] . Estimate (4.2) follows in a standard way from Lemma 2.2, Theorem 3.1 for the processes![]() . Thus, it only remains to verify the finiteness of the fractal dimension of
. Thus, it only remains to verify the finiteness of the fractal dimension of![]() . In order to prove this, we first note that, according to the Hölder continuities Theorem 2.1 in [13] and (4.7), we have
. In order to prove this, we first note that, according to the Hölder continuities Theorem 2.1 in [13] and (4.7), we have
![]()
for all![]() ,
, ![]() and
and![]() . Since the map
. Since the map ![]() are uniformly Lipschitz conti- nuous, Theorem 3.1 in [13] implies that
are uniformly Lipschitz conti- nuous, Theorem 3.1 in [13] implies that
![]()
for a given![]() , and some constant
, and some constant ![]() and
and ![]() which are independent of
which are independent of![]() . The proof of Theorem 4.1 is completed. ,
. The proof of Theorem 4.1 is completed. ,
5. Infinite-Dimensional (Uniform) Exponential Attractor and Non-Autonomous Exponential Attractor
Finally, we compare the non-autonomous exponential attractor ![]() obtained above with the so-called infinite-dimensional (uniform) exponential attractor constructed in [11] [13] . To the existence of the uniform at- tractor for strongly damped wave equations, we use the results in [4] and [5] as a model example.
obtained above with the so-called infinite-dimensional (uniform) exponential attractor constructed in [11] [13] . To the existence of the uniform at- tractor for strongly damped wave equations, we use the results in [4] and [5] as a model example.
Let ![]() be some external force. Let
be some external force. Let ![]() be the hull of
be the hull of ![]() in
in![]() , i.e.,
, i.e.,
![]()
where ![]() denotes the closure in
denotes the closure in![]() . Evidently,
. Evidently, ![]() for any
for any![]() .
.
Using the standard skew product flow in [4] and [5] , for every external forces ![]() satisfying (1.5), we can embed the dynamical process
satisfying (1.5), we can embed the dynamical process ![]() into the autonomous dynamical system
into the autonomous dynamical system ![]() acting on the extended phase space
acting on the extended phase space ![]() via
via
![]()
It is known that ![]() is a semigroup. If this semigroup possesses the global attractor
is a semigroup. If this semigroup possesses the global attractor![]() , then, its projection
, then, its projection ![]() onto the first component of the Cartesian product is called the uniform at- tractor associated with problem (1.1).
onto the first component of the Cartesian product is called the uniform at- tractor associated with problem (1.1).
It is also known that the uniform attractor ![]() exists under the relatively weak assumption that the hull
exists under the relatively weak assumption that the hull ![]() is compact in
is compact in![]() , but, unfortunately, for more or less general external forces
, but, unfortunately, for more or less general external forces ![]() its Haus- dorff and fractal dimensions are infinite. Instead, the following estimate for its Kolmogorov’s
its Haus- dorff and fractal dimensions are infinite. Instead, the following estimate for its Kolmogorov’s ![]() -entropy holds, see [4] .
-entropy holds, see [4] .
Proposition 5.1 Let the above assumptions hold and the hull ![]() of the initial external forces be compact. Then, Equation (1.1) possesses the uniform attractor
of the initial external forces be compact. Then, Equation (1.1) possesses the uniform attractor ![]() and its
and its ![]() -entropy can be estimated in terms of the
-entropy can be estimated in terms of the ![]() -entropy of the hull
-entropy of the hull ![]() as follows:
as follows:
![]() (5.1)
(5.1)
for some positive constants ![]() and
and ![]() depending on
depending on![]() .
.
Definition 5.1 [11] [13] A set ![]() is an (uniform) exponential attractor of Equation (1.1) if the fol- lowing properties are satisfied:
is an (uniform) exponential attractor of Equation (1.1) if the fol- lowing properties are satisfied:
1) Entropy estimate: ![]() is a compact subset of the phase space
is a compact subset of the phase space ![]() which satisfies estimate (5.1) (possibly, for larger constants
which satisfies estimate (5.1) (possibly, for larger constants ![]() and
and![]() ).
).
2) Semi-invariance: for every ![]() there exists
there exists ![]() such that
such that ![]() for all
for all ![]()
3) Uniform exponential attraction property: there exists a positive constant ![]() and a monotonic function
and a monotonic function ![]() such that, for every
such that, for every ![]() and every bounded subset
and every bounded subset![]() , we have
, we have
![]() (5.2)
(5.2)
[13] points out that a uniform exponential attractor ![]() can be constructed if the (non-autonomous) exponential attractor
can be constructed if the (non-autonomous) exponential attractor ![]() has been constructed, so we have
has been constructed, so we have
Theorem 5.1 Let the assumptions of Theorem 4.1 hold and let, in addition, the hull ![]() of some external forces satisfying (1.5) be compact. Then, there exists a uniform exponential attractor
of some external forces satisfying (1.5) be compact. Then, there exists a uniform exponential attractor ![]() for problem (1.1) which can be constructed as follows:
for problem (1.1) which can be constructed as follows:
![]()
Remark 1 When![]() , Equation (1.1) reduces to the following damped wave equation on a bounded domain
, Equation (1.1) reduces to the following damped wave equation on a bounded domain ![]() with smooth boundary
with smooth boundary![]() :
:
![]() (5.3)
(5.3)
Equation (1.1) reduces to the damped wave equation modeling the Josephson junction in superconduction which was studied by many authors (see [1] [6] [17] ). We assume that the function ![]() satisfy (1.2)-(1.4). The Equation (5.3) also possesses a finite dimensional exponential attractor.
satisfy (1.2)-(1.4). The Equation (5.3) also possesses a finite dimensional exponential attractor.
Remark 2 When![]() , Theorem 4.1 remains valid for the following strongly damped wave equation was studied by many authors (cf. [7] [18] ):
, Theorem 4.1 remains valid for the following strongly damped wave equation was studied by many authors (cf. [7] [18] ):
![]()
if we assume that the function ![]() satisfy (1.2)-(1.4).
satisfy (1.2)-(1.4).
Acknowledgements
This work is supported by the National Natural Science Foundation of China (11101265) and Shanghai Edu- cation Research and Innovation Key Project of China (14ZZ157).