Fractional Langevin Equation in Quantum Systems with Memory Effect ()
1. Introduction
Application of the fractional calculus on physics has attracted an increasing attention this decade including physical kinetics [1] , anomalous transport theory in solid-state physics [2] , and nonlinear dynamics [3] . These applications aim to explore the nonlocal quantum phenomena found for either long-range interactions or time-dependent processes with long-time memory effect. Fractional space and time derivatives are used to describe these systems with nonlocal dynamics, e.g. anomalous diffusion or fractional Brownian motion [4] [5] . Recently, the fractional time derivative is given a physical interpretation by Iomin which describes an effective interaction of a quantum system with its environment [6] . Here we will introduce the practical quantum system with long-time memory effect [7] .
Quantum information systems are currently attracting enormous interest for their fundamental nature and potential applications to computation and secure communication. Many novel methods have been proposed to generate controllable qubit states through the environment of the qubits [8] -[10] . When a qubit made of a twolevel atom is embedded inside a structured reservoir with memory effect, the correlation between the qubit and environment will affect the dynamics of the qubit [7] [11] [12] . In this case, the effective interaction of the qubit with the photon modes of the environment is expressed as a memory kernel. In this paper, we take a particular memory kernel of an anisotropic photonic crystal (PhC) as an example to illustrate the method and suitability of applying fractional calculus to this qubit system. We find that the kinetic equation can be expressed as a fractional generalized Langevin equation (FGLE) when the fractional time derivative is used to express memory kernel term. The expression of FGLE opens a new route for the application of fractional calculus to quantum information systems.
This paper is organized as follows. In Section 2, we present a FGLE for the quantum system with memory effect. The general solution of this FGLE is expressed in terms of two-parameter Mittag-Leffler function through the methodology of Laplace transform. In Section 3, a particular memory kernel characterizing the quantum system of a qubit in an anisotropic PhC is used to illustrate the solving procedures of the FGLE. Based on the analytical solution of this FGLE, we study the dynamics of the qubit energy, polarization and von Neumann entropy. Finally, we summarize our results in Section 4.
2. Fractional Langevin Equation
When the quantum system with memory effect is considered, the general form of the kinetic equation can be derived from the time dependent Schrődinger equation as
(1.1)
where 
denotes the time evolution of the quantum system and 
the memory kernel of the reservoir. This kinetic equation reads that the future of the system is determined by the memory of the reservoir in its previous state.
To solve Equation (1.1), we introduce the Laplace transform. When the Laplace image of the memory kernel 
is considered, we need to construct a Cantor set with infinite number of divisions of time interval because no characteristic time scale exists in this memory kernel. As the Cantor set is constructed, we could choose the entire time interval as 
with unity height. When the central part of the time interval is removed, the interval leaves two intervals with length
. In order to keep the integral memory, the heights of the two intervals must be increased from unity to the value
. In the next stage, each remaining interval with length 
is subjected to the same division process. As the division process is performed 
times, the memory kernel in Laplace image will be represented by a set of 
intervals with length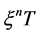 
and height
. The integral of the memory kernel in Laplace image is approached as the division time 
is taken to be infinity. This approach leads to the Laplace transform of the memory kernel has the form of 
with 
being the fractal dimension of time blocks participating in the construct of the Cantor set.
As the inverse Laplace transform is performed on the kernel
, we obtain the memory kernel approximately as
(1.2)
with Gamma function
. Substituting this memory kernel into Equation (1.1), we have the kinetic equation as
(1.3)
Comparing the right-hand-side term of this equation with Riemann-Liouville fractional derivative
(1.4)
we could express the kinetic equation as a differential equation with fractional order, i.e.,
(1.5)
In order not to lose the initial conditions of the quantum systems, we apply the integral operator (
) to this equation and obtain
. (1.6)
This differential equation with negative fractional order could be further processed through manipulating the fractional differential operator. This manipulation yields
(1.7)
Here we have expressed the kinetic equation of this quantum system with memory effect as a FGLE through using the fractional time derivative for the memory kernel.
When we proceed to solve the FGLE through Laplace transform, we need the formula of Laplace transform in fractional order
(1.8)
with Laplace variable
. Here the operator of fractional calculus 
is defined as
(1.9)
with 
being the real part of the order 
and the fractional derivative 
being defined through the Riemann-Liouvile form in Equation (1.4). And the Laplace transform of exponential order 
could be obtained from elementary calculus as
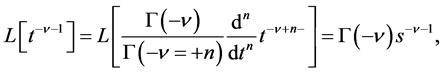(1.10)
if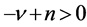
. With these two formula, the Laplace transform of the FGLE has the algebraic form as
(1.11)
This algebraic form could be expressed as a sum of partial fractions as
(1.12)
with expansion coefficients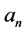 
and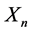 
being the roots of the indicial Equation (1.11).
When the inverse Laplace transform is performed on these fractional expansions of
, we need the formula
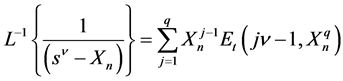(1.13)
with positive integer 
and the two-parameter Mittag-Leffler function
. The analytical solution of the FGLE is obtained as
(1.14)
which is a linear combination of the two-parameter Mittag-Leffler functions. These two-parameter MittagLeffler functions are defined as
(1.15)
with the derivative formula
(1.16)
They are related to the one-parameter Mittag-Leffler function 
through 
with positive integer 
[4] .
3. A Particular Memory Kernel
In this section, we consider a quantum system of a qubit in an anisotropic photonic crystal (PhC) with a particular memory kernel as shown in Figure 1. The Hamiltonian of this quantum system is
(1.17)
Here the atomic operators 
obey the commutation relation of 
with the Kronecker delta function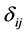
. And the photon operators 
and 
follow the commutation rules of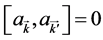
, 
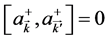and
. The frequency 
stands for the atomic transition frequency from excited state 
to ground state 
and 
for the photon mode frequency of the reservoir with wavevector
. The coupling strength between the atom and the photon (electromagnetic field) is characterized by
with the fixed qubit dipole moment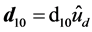
, sample volume
, dielectric constant 
and polarization unit vector 
of the photon mode with frequency
.
As we assume only one photon is created or annihilated for one atomic transition (single-photon sector), the wave function of the system has the form
(1.18)
with the initial condition
, 
and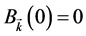
. The equations of motion for the amplitudes
, 
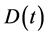and 
can be obtained when we project the time-dependent Schrődinger equation 
on the single-photon sector of the Hilbert space as
(1.19)
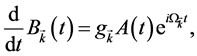(1.20)
and
(1.21)
with detuning frequency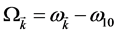
. The two Equations of (1.19) and (1.20) can be combined as
(1.22)
with the memory kernel
. This evolution equation relates the excited amplitude 
of the qubit to the reservoir memory through the memory kernel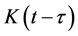
. For the anisotropic PhC reservoir, this memory kernel has a particular form of
(1.23)
with the coupling constant 
and the detuning frequency 
of the qubit transition frequency 
from the band edge frequency 
[7] . With this special form of memory kernel, the kinetic equation of the excited amplitude 
becomes
(1.24)
if the transformation 
is performed. Here we express this memory effect as a fractional time derivative which describes the effective interaction of the qubit with the environmental PhC reservoir. That is, the right-hand-side term of the kinetic Equation (1.24) is written as a Riemann-Louville fractional time derivative with order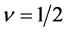 
and 
such that
(1.25)
This expression leads to the fractional form of the kinetic equation as
(1.26)
We define this fractional differential equation as a fractional generalized Langevin equation (FGLE) of this quantum system. We solve this FGLE by applying Laplace transform and obtain
(1.27)
Here 
is the Laplace transform of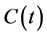 
with the initial condition
. In order to find the solution of this excited amplitude, standard procedures of expressing this algebraic equation as a sum of partial fractions and performing inverse Laplace transform on these partial fractions are taken. In the first step, we need to find the roots of the indicial equation
, where the variable 
has been converted into
. Two kinds of roots exist in this indicial equation: one with different roots 
and the other with degenerate root
. For the case of different roots, 
is expressed as
(1.28)
with
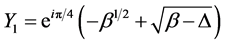(1.29)
and
(1.30)
For the degenerate case, we have 
which leads to the indicial equation as
. The partial fractions of 
is thus written as
(1.31)
As the inverse Laplace transform is applied to these partial-fractional forms of 
with fractional powers of the variables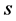
, we use the formulas of
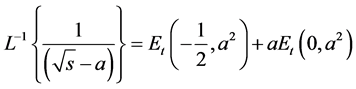(1.32)
and
(1.33)
with the fractional exponential function
, whose definition and properties are listed in Equations (1.15) and (1.16). This procedure leads to the solution of the fractional kinetic equation being expressed as the linear combination of the fractional exponential functions such that
(1.34)
for the different-root case
; and
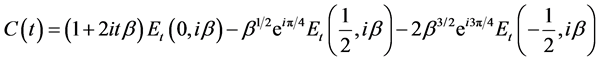(1.35)
for the degenerate case
. Based on this analytic solution, we can obtain the reduced density matrix of the qubit from the wave function in Equation (1.18) through tracing over the reservoir degrees of freedom as
(1.36)
The elements in this matrix are associated with the information of the qubit energy and coherence. In the following, we will study the dynamics of the excited-state energy, polarization and von Neumann entropy of the qubit.
3.1. Excited-State Probability
We show the time evolution of the qubit excited-state energy through the probability 
in Figure 2. The energy dynamics exhibits oscillatory behavior and does not decay with time as the qubit frequency lies inside the photonic bang gap (PBG) region (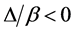
). The memory effect of this quantum system is observed directly through these trapping states of the qubit energy.
3.2. Polarization Dynamics
As a qubit interacts with the environment, it will randomize the polarization of the qubit. The quantum phase information of a qubit carried by the qubit polarization will thus escape from the qubit into the environment through this randomization of polarization and lead to the quantum decoherence. Here we show the polarization dynamics in Figure 3 through the expression of qubit polarization 
(if
). The polarization dynamics of the qubit with frequency lying inside the PBG region (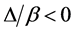
) exhibits non-decaying oscillation. The qubit loses partial of its polarization in the very beginning period of time and then preserves the remaining polarization through the steady oscillation. This trapping state of the qubit polarization reveals the memory effect of the system which leads to the preservation of the qubit phase information.
3.3. Dynamics of von Neumann Entropy
Entropy, a measurement of information amount stored in a qubit, will be changed as the qubit is correlated to the environment. The correlation between the environment and the state will transform the initially pure state of the qubit into a finally mixed state where the amount of information of the qubit is changed. For a qubit state with density matrix
, von Neumann entropy is defined as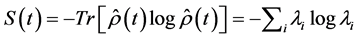 
with 
being the eigenvalues of the matrix
. for the density matrix in Equation (1.36), we show the von Neumann entropy in Figure 4 for the initially excited qubit (
). The entropy has its minimal value zero at 
and reaches its maximal value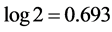 
at the very beginning of time. After a period of time on the order of the decay timescale, the entropy becomes steady with nonzero value for the qubit frequency in PBG region (
). This result shows that the initially pure system becomes maximally mixed in the very beginning period of time. As the qubit equilibrating with the PhC reservoir, the system becomes steady with less mixed state. The trapping state of the von Neumann entropy reveals that the amount of information stored in the qubit
Figure 2. (Color online) Dynamics of the qubit excitedstate probability with different detuning frequencies 
from the band edge frequency
.
Figure 3. (Color online) Dynamics of the qubit polarization for the qubit frequency lying inside 
and outside 
the band gap.
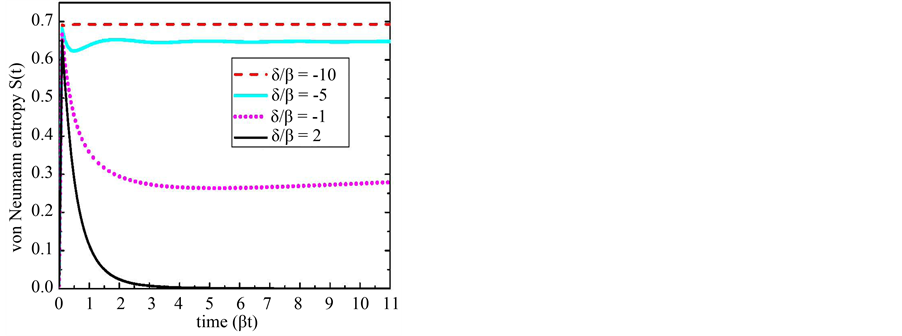
Figure 4. (Color online) Dynamics of the von Neumann entropy for different qubit frequencies.
is preserved through the steady mixed state. The memory effect of the system is observed directly through the preservation of the qubit information.
4. Conclusion
We have used the fractional time derivative to express the kinetic equation of the quantum system with memory effect as a FGLE. For a particular memory kernel, we obtain the solution of the FGLE in terms of the twoparameter Mittag-Leffler function. In the study of the qubit dynamics in the particular memory kernel of an anisotropic PhC, we observe the memory effect directly through the trapping states of the qubit energy, polarization and von Neumann entropy.
Acknowledgements
We would like to gratefully acknowledge partially financial support from the National Science Council (NSC), Taiwan under Contract Nos. NSC 102-2811-M-034-002, NSC 102-2112-M-034-001-MY3 and NSC 102-2112- M-009-016-MY3.
NOTES
*Corresponding authors.