1. Introduction
The nature of interactions between nucleons is one of the fundamental and essential concepts of nuclear physics. It is required to clarify the nuclear structure of nucleus which comprises of relativistic spin-1/2 particles. The Dirac equation is the most perfect example of a relativistic equation which is able to describe the relativistic effects in a simple manner. In recent years, considerable attention has been paid to exactly solvable Dirac equation [1] . To the best of our knowledge, this equation is exactly solvable for only a few simple interactions and the solutions usually come with a strong constraint on the potentials [2] . For example, some authors assumed that the scalar potential is equal to the vector potential and obtained the exact solution of Dirac equation with some typical simple potentials by using different methods. These investigations include the harmonic oscillator potential [3] , the triaxial and axially deformed harmonicoscillator potential [4] , Eckart potential [5] [6] , Woods-Saxon potential [7] , Hulth´en potential [8] , pseudo harmonic oscillator [9] and ring-shaped Kratzer-type potential [10] , ring-shaped non-spherical oscillator [11] and double ring-shaped oscillator potential [12] , Hartmann potential [13] [14] , Rosen-Morse type Potential [15] , generalized symmetrical double-well potential [16] , Scarf-type potential [17] , etc. [18] . The methods include the standard method, super symmetry quantum mechanics [5] [19] and [20] , and the Nikiforov-Uvarov (NU) method [21] and so on. Formerly, Yukawa potential has been used in nonrelativistic quantum mechanics to study the interactions between nonrelativistic particles. Recently there has been much interest in solutions of Dirac equation for spin-1/2 particles with high energies [22] . In addition, thespin and pseudospin symmetry [23] [24] has been originally observed almost about 40 years ago as a mechanism to explain different aspects of the nuclear structure with relativistic spin-1/2 particles. Ginocchio has shown that the pseudospin symmetry arises from the near equality of the magnitude of the attractive scalar potential S(r) and the repulsive vector potential V(r), i.e., S(r)
‒V(r) in nuclei. The pseudospin symmetry refers to a quasi-degeneracy of the single-particle doublets and can be characterized with the quantum numbers (n, l, j = l + 1/2) and (n ‒ 1, l + 2, j = l + 3/2), where n, l and j are the radial, orbital and total angular momentum quantum numbers for a single particle, respectively. The spin symmetry and the pseudospin symmetry occur for 
and 
in Dirac equation [25] -[27] . The screened Coulomb potential is used in various areas of physics to model singular but short-range interactions [28] [29] . In high energy physics, for example, it is used to model the interaction of hadrons in short range gauge theories where coupling is mediated by the exchange of a massive scalar meson [28] [30] . In atomic and molecular physics, it represents a screened Coulomb potential due to the cloud of electronic charges around the nucleus. It has also been used to describe the interaction between charged particles in plasma, solid and colloidal suspensions [31] .
In this work, we have obtained the energy equation of relativistic spin-1/2 particles with the consideration of spin symmetry and pseudospin symmetry case. Solution of Dirac equation with standard Yukawa potential is presented by using the Nikiforov-Uvarov (NU) method and the eigen functions related to these cases of Dirac equation are obtained. Standard Yukawa-potential is given by
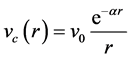, (1)
where 
and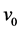 
are range of nuclear force and strength of potential, respectively [28] .
2. Dirac Basic Equation for Spin-1/2 Particles
In the relativistic description, the Dirac equation for a single-nucleon with the mass of M moving in an attractive scalar potential S(r) and a repulsive potential V(r) in natural units 
can be written as [32] :
, (2)
where E is the relativistic energy, P is the momentum operator, and 
are the 4 ´ 4 Dirac matrices as follows:
, (3)
I is the unit matrix and 
represents Pauli matrices. For a particle in a central field, the total angular momentum J and 
commute with the Dirac Hamiltonian, where L is the orbital angular momentum. For a given total angular momentum j, the eigenvalues of 
are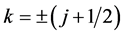
, where the negative sign is related to aligned spin and the positive sign represents the unaligned spin. The wave functions can be classified according to their angular momentum j and spin-orbit quantum number k as follows:
, (4)
where 
and 
are the upper and lower components, 
and 
are the spherical harmonic functions. 
is the radial quantum number and m is the projection of the angular momentum on the z-axis. The orbital angular momentum quantum numbers 
and 
are related to the spin and pseudospin quantum numbers. Substituting equation (4) into equation (2), we obtain a couple of equations for the radial part of the Dirac equation as follows:
, (5)
. (6)
By eliminating 
in Equation (5) and 
in equation (6), we obtain the following two secondorder differential equations for the upper and lower components:
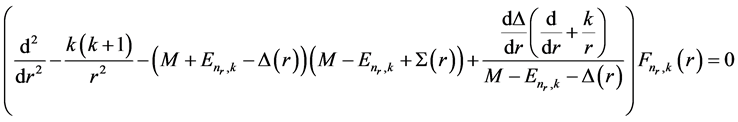, (7)
. (8)
where 
and 
are the difference and the sum of the potentials V(r) and S(r), respectively [26] [27] . We consider the bound state solution that demands the radial components satisfying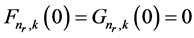 
and
.
3. Spin Symmetry Solution
This symmetry arises from the near equality in magnitudes of an attractive scalar, S(r), and repulsive vector, V(r), relativistic mean field, 
in which the nucleon moves [29] . In this case
, and equation (7) reduces to
, (9)
where 
for 
and 
for
. The energy eigenvalues depend on 
and
. By inserting the standard Yukawa potential instead of 
in Equation (9) we get
. (10)
This equation is a combination of the exponential and inverse square potentials, which cannot be solved analytically by using the standard methods such as SUSY or NU. Therefore, we must find an approximation to Yukawa potential term to solve the equation analytically. Considering the Taylor expansion, we adopt the approximation bellow [33] :
.(11)
Rewriting Equation (10) with above term yields
, (12)
. (13)
If we introduce the notations
, (14)
and
. (15)
We obtain
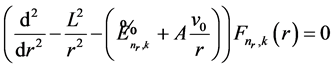. (16)
To solve this equation, we consider
, (17)
So we can rewrite Equation (16) as
. (18)
It is known that the solution of the second order differential equations plays an essential role in studying many important problems of theoretical physics. At this point, the NU method can be used to solve these types of equations.
4. Basic Concepts of NU Method
The NU method has been used to solve Schrodinger, Dirac, Klein-Gordon wave equations for certain kinds of potentials [34] . In this method the differential equations can be written in the following form:
, (19)
where 
and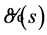 
are polynomials that can be at most second degree, and 
is a first-degree polynomial. To find a particular solution for Equation (19) by separation of variables, we have the following transformation:
. (20)
It reduces Equation (19) to a hyper-geometric type function:
. (21)
The function φ(s) is defined as a logarithmic derivative
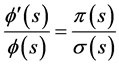, (22)
y(s) is the hypergeometric type function whose polynomial solutions are given by Rodrigues relation:
, (23)
Bn is the normalizing constant and the weight function ρ must satisfy the following condition:
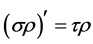. (24)
The function π and the parameter λ required for this method are defined as:
, (25)
π(s) is a polynomial with the parameter s and the determination of k is the essential point in the calculation of π(s). In order to find the value of k, the expression under the square root must be square of a polynomial, so we have a new eigenvalue equation:
, (26)
where
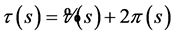, (27)
and it will have a negative derivative. By comparing (25) and (26), we obtain the energy eigenvalues [34] .
If we apply the NU method, by comparing (18) and (19), the following expressions are obtained:
. (28)
Substituting the above expression into (25), we have:
. (29)
The constant parameter 
can be determined from the condition that the expression under the square root must be the square of a polynomial of first degree. So, it has a double zero. Therefore, possible forms of π(r) are as follows:
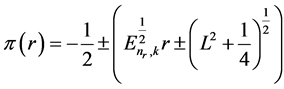. (30)
Since we have the polynomial 
and it has a negative derivative, the suitable form is established. Therefore,
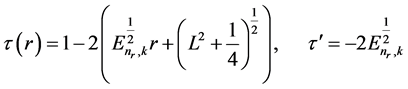. (31)
According to (22) and (24) these values can be obtained:
(32)
. (33)
Substituting (33) into (23), yn can be found:
. (34)
By using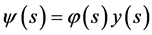
, the solution of (16) can be written as the wave function of the Dirac equation as follow:
. (35)
Considering the notations of (14), (15) and Equation (26) the eigenvalues of energy can be obtained:
. (36)
This equation can be used to determine the difference in energy between energy levels of spin-1/2 particles with spin symmetry.
5. Pseudospin Symmetry Solution
Now we return to Equation (8) under pseudospin symmetry, i.e.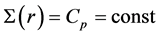
. with the consideration of Equation (11), Equation (8) reduces to:
. (37)
If we introduce the notations:
, (38)
and
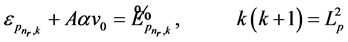. (39)
We will obtain:
. (40)
In order to solve the above equation, as we did in Equation (17), we consider:
. (41)
So we can rewrite Equation (41) as:
. (42)
Applying the NU method and comparing (42) and (19), the following expressions are obtained:
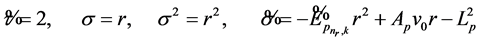. (43)
Using (25), π(r) can be found as follow:
. (44)
The constant parameter 
can be determined from the condition that the expression under square root must be the square of a polynomial of first degree. So, it has a double zero, therefore possible forms of π(r) are:
. (45)
Since the polynomial 
has a negative derivative, we have:
. (46)
According to (22) and (24) these values can be obtained:
, (47)
. (48)
Substituting (48) into (23), yn can be written as:
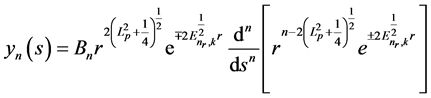. (49)
Using
, the solution of (37) can be written as the wave function of Dirac equation under the pseudospin symmetry as follow:
. (50)
Finally, considering the notations (38), (39) and Equation (26), the eigenvalues of energy can be obtained:
. (51)
This energy equation yields the energy levels of spin-1/2 particles with pseudospin symmetry.
6. Conclusion
In this study, the energy equations of relativistic spin-1/2 particles are calculated with the consideration of spin symmetry and pseudospin symmetry case. The analytical NU method is applied to obtain the energy spectrum and eigen functions related to these cases of Dirac equation with standard Yukawa interaction.