1. Introduction
There exists an intimate relationship between classical geometry and physics, and to appreciate this we will consider the Einstein field equations (EFE) of special relativity written as:
(EFE)
where 
is the Einstein tensor,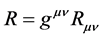 
is the Ricci tensor. 
is the energy-momentum tensor.
For the moment we are only interested in three basic properties of the above equation.
1) The equation (EFE) is a tensor equation. This is necessarily so, since the principle of invariance under coordinate transformations must hold, in other words the equations of physics must look the same in any frame of reference.
2) We can interpret equation (EFE) more simply as
i.e. it is the presence of matter in space that distorts the neighbouring geometry. Most equations of mathematical physics can be interpreted similarly.
3) The solution to equation (EFE) is a geometrical object, namely a line element given by
where 
is the metric tensor to be solved for in (EFE).
1.1. Quantum Geometry
Every geometry is associated with some kind of space. Quantum (or noncommutative) geometry [1] [2] deals with quantum spaces, including the classical concept of space as a very special case. In classical geometry spaces are always regarded as collections of points equipped with the appropriate additional structure (as for example a topological structure given by the collection of open sets, or a smooth structure given by the atlas). In contrast to classical geometry, quantum spaces are not interpretable in this way. In general, quantum spaces have no points at all! They exhibit non-trivial quantum fluctuations’ of geometry at all scales.
In generalizing classical geometry to the non-commutative level, there are two important conceptual steps:
1) Translation of geometry into a commutative algebra format;
2) Non-commutative generalizations.
1.2. Reformulating Basic Geometrical Concepts
It turns out that the geometrical structure on any given topological space X is always completely expressible in the language of some associated *-algebra [3] [4] .
Points
Let X be a compact topological space, and let
be the
*-algebra of continuous complex-valued functions on X. Every element
naturally gives rise to a linear functional
defined by
This map is multiplicative in the sense that
Furthermore, 
is Hermitian in the sense that 
it is also non-zero, i.e. 
is a character on A. Conversely, consider an arbitrary character
, then it can be shown that there exists a unique point 
such that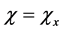
. In other words, we have a natural bijection between points of X and characters of A. It is important to note that this characterization of points also remains valid at the smooth level, in which X could be a compact smooth manifold and the associated *-algebra consists of smooth functions on X.
1.3. The Gelfand-Naimark Theorem
The algebra 
of complex-valued functions on a compact topological space X, equipped with the maximum norm
is a commutative C*-algebra [2] . The classical theorem of Gelfand and Naimark characterizes the algebras of the form
, as commutative unital C*-algebras. This means that for every commutative unital C*-algebra A there exists (up to homeomerphisms) a unique compact topological space X such that
.
As we have earlier observed, the points of the space X are recovered as characters of the associated algebra A. In terms of this identification, the topology on X coincides with the weak*-topology, induced from the dual space
, consisting of continuous linear functionals on A. It turns out that homomorphisms between C*-algebras are automatically continuous, in particular characters are continuous linear functionals.
2. The Quantum Plane
A simple example of quantum geometry is the quantum plane (Figure 1). Usually, a plane is described by two coordinate functions x, y. Naturally, the functions xy and yx are the same since it does not matter whether you measure x first and then y or y first and then x. This is precisely what is lost in the quantum world.
In the quantum plane we replace the property 
by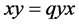 
where q is some parameter. We no longer have points, however we can continue to work algebraically with x and y.
Define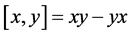
, the commutator bracket. Hence 
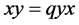can be rewritten as
The commutative case is obtained when
.
2.1. q-Deformed Calculus
It is interesting to know that one can really do geometry in this setting, where coordinates do not commute. This is the remarkable discovery in recent times. For example, we can follow the approach of Newton-Leibnitz defining differentiation by
But when 
and in particular 
we get instead
Thus for example the derivative of the function 
in this non-commutative setting would be
We observe here that when 
the derivative of 
for the commutative case is obtained, i.e.
.
2.2. Basic Notions of q-Calculus
The mathematical study of noncommutative geometry is intimately related to the so-called q-calculus (qnumbers, q-factorials, q-differentials and integrals, basic q-hypergeometric functions, and q-orthogonal polynomials). Here we give a brief introduction to q-numbers and q-factorials which will be required in the subsequent sections.
2.2.1. q-Numbers and q-Factorials
For any nonzero complex number q, the q-number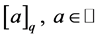
, is defined by
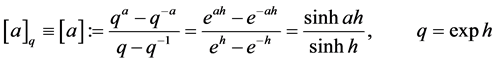(2.1)
Figure 1. The quantum plane (xy ≠ yx).