1. Introduction
Let X and Y be two random variables independently distributed real intervals  and
and  respectively. Let
respectively. Let  and
and  be the probability distribution functions of X and Y respectively.
be the probability distribution functions of X and Y respectively.
Let  and
and  the juxtaposition of events
the juxtaposition of events  and
and  would give us the interval
would give us the interval . Observe that while
. Observe that while 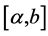 and
and  are simple probabilistic events,
are simple probabilistic events,  is totally reference as an event because its boundaries are from two probabilistic populations. For simplicity let us call
is totally reference as an event because its boundaries are from two probabilistic populations. For simplicity let us call  a twopopulation event (t.p.e.), we are interested to calculate the probability associated with such a t.p.e., and thereafter to explain its physical significance.
a twopopulation event (t.p.e.), we are interested to calculate the probability associated with such a t.p.e., and thereafter to explain its physical significance.
2. Simple and Compound Two-Population Events
Let  be a t.p.e. It is easy to see that
be a t.p.e. It is easy to see that
 (1)
(1)
In other words, in terms of intervals
 (2)
(2)
The identities (1) and (2) are rather elementary. But (2) in particular can have far reaching consequences, which we are going to assert later. The t.p.e.  is a simple t.p.e. in the sense, that if
is a simple t.p.e. in the sense, that if  and
and  are t.p.e.’s, we shall call
are t.p.e.’s, we shall call  a compound t.p.e.
a compound t.p.e.
Let 

 , and
, and .
.
It is easy to see that

Similarly

Therefore for the compound t.p.e.
 (3)
(3)
In the same way,

Similarly

Therefore,
 (4)
(4)
Identities (3) and (4) give us the probabilities of union and intersection respectively of two simple two population events.
Our discussions on probability of a t.p.e. ends here. In what follows, we shall explain the physical significance of identity (2). It would thereafter be shown that a t.p.e. is indeed a possibilistic event.
3. Physical Significance of a Two-Population Event
Zadeh ([1] ) introduced the mathematics of fuzziness long forty nine years ago. It has made inroads into almost all applied branches of knowledge. However, most of the mathematicians shy away from this branch of mathematics for various reasons. One such is the belief that randomness and fuzziness are two independent concepts.
In this section we shall show the following:
a) Randomness can actually be at the root of fuzziness.
b) Two independent probability laws can define a fuzzy number.
First, let us review certain necessary definitions.
3.1. Some Basic Definitions Related to Fuzziness
Let E be the universe of discourse. A fuzzy set A in E is characterized by a membership function 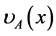 lying in
lying in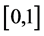 .
. 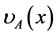 for
for  represents the grade of membership of x in A. Thus a fuzzy set A is defined as
represents the grade of membership of x in A. Thus a fuzzy set A is defined as

A fuzzy set A is said to be normal if 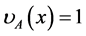 for at least one
for at least one 
An a-cut of a fuzzy set is an ordinary set of elements with membership grade greater than or equal to a threshold a, . Thus an a-cut Aa of a fuzzy set A is characterized by [2]
. Thus an a-cut Aa of a fuzzy set A is characterized by [2]

A fuzzy set is said to be convex if all its a-cuts are convex sets [2] .
A fuzzy number is a convex normalized fuzzy set A defined on the real line E such that i) there exists an  such that
such that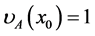 , and ii)
, and ii)  is piecewise continuous.
is piecewise continuous.
Indeed, if  is a real interval with a < b < c, for a fuzzy number denoted by
is a real interval with a < b < c, for a fuzzy number denoted by 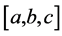 with
with , and
, and .
.  for
for  is known as left reference function and
is known as left reference function and  for
for  is known as the right reference function of the fuzzy number
is known as the right reference function of the fuzzy number 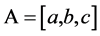 (L-R fuzzy number) [3] . For such an L-R (left-right) fuzzy number, the left reference function is non-decreasing and the right reference function is non-increasing. Finally, the membership function of a fuzzy set is viewed as its possibility distribution [4] .
(L-R fuzzy number) [3] . For such an L-R (left-right) fuzzy number, the left reference function is non-decreasing and the right reference function is non-increasing. Finally, the membership function of a fuzzy set is viewed as its possibility distribution [4] .
3.2. Set Superimposition
When we overwrite, the overwritten portion looks darker. Indeed, the doubly represented portion looks doubly dark. To explain this, we would need a set operation (S) of superimposition of two sets A and B defined as:
 (5)
(5)
where  are the elements of
are the elements of  represented twice, and (+) represents union of disjoint sets.
represented twice, and (+) represents union of disjoint sets.
If  and
and  are two real intervals such that
are two real intervals such that , we would get from (5)
, we would get from (5)
 (6)
(6)
where ,
, 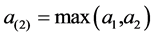 ,
,  , and
, and .
.
Identity (6) explains why-if two line segments are superimposed, the common portion looks doubly dark [5] . Mazarbhuiya et al. used this operation to define fuzzy arithmetic operations [6] and to solve a fuzzy equation [7] . Set superimposition is also used in mining temporal data ([8] [9] ). In ([10] [11] ), Baruah tries to establish link between probability law and possibility law.
Let now,  and
and  be two fuzzy sets with constant membership 1/2 everywhere.
be two fuzzy sets with constant membership 1/2 everywhere.
Following (6) we can write:
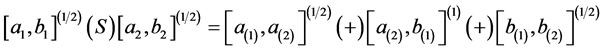 (7)
(7)
An obvious extension of (7) is: if  are values of
are values of  arranged in ascending order, and
arranged in ascending order, and  are values of
are values of  are arranged in ascending order, we would get
are arranged in ascending order, we would get
 (8)
(8)
At this point, we would need a classical result from order statistics to proceed further.
3.3. The Glivenko-Cantelli Theorem
Define
 (9)
(9)
where  are realizations of a random variable X, and
are realizations of a random variable X, and 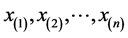 are
are  arranged in ascending order.
arranged in ascending order.
F(x) is random here with

where  is the underlying theoretical distribution function.
is the underlying theoretical distribution function.  being an empirical distribution function.
being an empirical distribution function.
In such a case, the Glivenko-Cantelli Theorem on order statistics [12] states that

This means,  uniformly in x with probability 1.
uniformly in x with probability 1.
3.4. The Glivenko-Cantelli Theorem Applied to Superimposed Equally Fuzzy Sets
Consider the identity (8) once again. Let X and Y be random and independently distributed in two real intervals  and
and  respectively. Let
respectively. Let  and
and 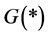 be the probability distribution functions of X and Y respectively.
be the probability distribution functions of X and Y respectively.
Application of Glivenko-Cantelli Theorem on identity (8) now after the imposition of randomness, as , on n superimposed equally fuzzy sets
, on n superimposed equally fuzzy sets ,
, 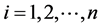 , gives us the following:
, gives us the following:
i) 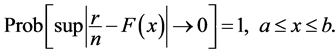
ii) (10)
(10)
In other words, a probability distribution function  in
in  can indeed be the left reference function, and a complementary probability distribution function or survival function
can indeed be the left reference function, and a complementary probability distribution function or survival function  in
in  can similarly be the right reference function of a fuzzy number.
can similarly be the right reference function of a fuzzy number.
We can therefore conclude that randomness can actually be at the root of fuzziness, and that two independent probability laws can define a fuzzy number.
4. Discussions
The possibility distribution function in , which indeed is the membership function of a fuzzy number
, which indeed is the membership function of a fuzzy number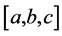 , can be viewed as two different functions, one in the interval
, can be viewed as two different functions, one in the interval  and the other in the interval
and the other in the interval . In
. In , if a probability law
, if a probability law , and in
, and in , if another probability law
, if another probability law 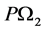 are defined such that
are defined such that  defines a fuzzy interval,
defines a fuzzy interval,  and
and  together can define the possibility distribution
together can define the possibility distribution  on
on . The fuzzy mathematicians have all along been trying to impose a
. The fuzzy mathematicians have all along been trying to impose a  on the same
on the same  on which
on which  is defined. For this mistake, they have all along been saying that fuzziness and randomness are two independent concepts.
is defined. For this mistake, they have all along been saying that fuzziness and randomness are two independent concepts.
In fact, every sample realization  can be thought of as values of unit fuzzy membership, around which intervals expressed as
can be thought of as values of unit fuzzy membership, around which intervals expressed as  would give us fuzzy numbers. Accordingly, in
would give us fuzzy numbers. Accordingly, in  there can be a probability law, while in
there can be a probability law, while in  there can be another probability law. Within the fuzzy number
there can be another probability law. Within the fuzzy number 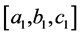 one can define possibilistic events, which are indeed t.p.e.’s defined in Section 1 of this article. Probabilities of such t.p.e.’s or possibilistic events, simple or compound, can be found following (2), (3) and (4). As long as one continues to impose a single probability law in a W where a possibility distribution is defined, the question of involving randomness to define fuzziness cannot arise. Independent probability laws on
one can define possibilistic events, which are indeed t.p.e.’s defined in Section 1 of this article. Probabilities of such t.p.e.’s or possibilistic events, simple or compound, can be found following (2), (3) and (4). As long as one continues to impose a single probability law in a W where a possibility distribution is defined, the question of involving randomness to define fuzziness cannot arise. Independent probability laws on 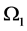 and
and , can finally define a possibility law on
, can finally define a possibility law on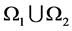 . In other words, possibility can indeed be a measure, and indeed it is a product measure.
. In other words, possibility can indeed be a measure, and indeed it is a product measure.
It is to be noted that identities (2) and (10) are directly related. In fact, (10) explains the physical significance of (2). We would like to conclude our discussions with an important comment. The fuzzy mathematicians invariably use the triangular fuzzy number in computations. No fuzzy mathematician has as yet supplied a logical answer as to why they use the triangular fuzzy number only. An obvious answer hidden in escapism is that it is simple to use. Simplicity of the triangular number in fact lies elsewhere. If 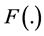 and
and  are uniform probability distribution functions, we simply get the triangular number. What we mean is: just as the uniform law is the simplest in the field of probability, so is the triangular number the simplest in fuzzy mathematics.
are uniform probability distribution functions, we simply get the triangular number. What we mean is: just as the uniform law is the simplest in the field of probability, so is the triangular number the simplest in fuzzy mathematics.
In other words, the simplicity of the triangular fuzzy number is rooted at the simplicity of the uniform probability law. This is the actual reason why the triangular number is simple.
To illustrate the concept, let us take a simple example. Let  be a normal fuzzy number whose membership function is given by
be a normal fuzzy number whose membership function is given by

where

is the Dubois-Prade left reference function and

is the Dubois-Prade right reference function. If we observe clearly, then we find that  is actually a probability distribution function whose probability density function is
is actually a probability distribution function whose probability density function is and
and  is a complementary probability distribution function or survival function whose probability density function is
is a complementary probability distribution function or survival function whose probability density function is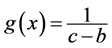 . This illustrates the fact that randomness can actually be at the root of fuzziness and two probability laws are sufficient to define a fuzzy number.
. This illustrates the fact that randomness can actually be at the root of fuzziness and two probability laws are sufficient to define a fuzzy number.
Acknowledgements
This work has been dedicated in honor of my beloved teacher Professor Hemanta K. Baruah, Former Dean of Science, Gauhati University, India and Current Vice Chancellor of Bodoland University, India.