1. Introduction
Pions are key carriers of strong interaction among mesons and hadrons. Hence, the knowledge of pion-nucleon and pion-nucleus is an important starting point to gain insight into the physics of strong interaction. For this and general purpose of understanding mesonic physics, many research facilities around the world dedicated to meson physics such as Los Alamos Meson Physics Facility (LAMPF), Swiss Institute of Nuclear research/PaulSherrer Institute (SIN/PSI), Tri-University Meson Facility (TRIUMF), Brookhaven National Laboratory (BNL), European Organization for Nuclear Research (CERN), National Laboratory for High Energy Physics (KEK), Joint Institute for Nuclear Research (JINR ) and others were built in the late 20th century [1] [2] .
Because of the very broad resonance associated with the 
-excitation of a nucleon, it has been customary to categorize the elastic scattering of pions in three energy bins, namely incident energies up to about 100 MeV, noted as below the 
-excitation, energies between 100 to 230 MeV, i.e. atop the broad 
-resonance and energies greater than that, i.e. above the 
-resonance [3] . The analyses reported in this paper cover the incident energies from 120 to 400 MeV. The kinetic energies being of the order of pion rest mass require a fully relativistic treatment to describe the reaction of the pions. Thus, this investigation is done using the full Klein-Gordon (K-G) equation unlike all previous ones which were usually done within the framework of an approximate version of K-G equation. The earliest works on pion-nucleus interaction were done using very limited data summarized in [4] [5] . The low-energy pion-nucleus elastic scattering data available at that time were primarily limited to forward angles and analyzed within the framework of non-local Kisslinger [6] , local Laplacian [7] and localequivalent of Kisslinger [8] potentials. All these theoretical models however, had only a limited success in explaining subsequent data taken at large angles. For explaining pion-nucleus scattering data in the delta resonance region at large angles, Satchler [9] proposed local potential similar to the one used in the optical model of nucleon-nucleus scattering using Schrödinger equation but considering relativistic kinematics (RSE). This paved the way for more pion-nucleus analyses using different local optical potentials [10] -[13] without recourse to the complexities of the non-local interaction. The successes of these potentials were reasonable but far from complete. In particular, all these analyses use RSE, which is an approximate form of the K-G equation.
Although Satchler’s potential showed a remarkable success in analyzing pion-nucleus experimental data, it fails to account for large-angle pion-nucleus data when his potential was used in the exact K-G equation [14] . Shehadeh et al. [14] then used an inverse scattering theory (IST), suggested first by Hooshyar and Razavy [15] and developed by Alam and Malik [16] for non-relativistic cases and then by Shehadeh and Malik [17] for the K-G equation to determine the nature of the functional form of the potential. The Satchler potential determined using RSE had to be modified when used in conjunction with the K-G equation to account for large-angle pion-nucleus data. The nature of the pion-nucleus potential seems to be undergoing important functional change between 120 to 400 MeV incident pion energies. The real part of the potential seems to be monotonic and attractive below the delta resonance, turning to be non-monotonic atop the resonance and becoming repulsive above the resonance. Similarly, the nature of the absorptive part is dominated by surface absorption below and atop the resonance. A goal of this research is to ascertain these using the phase shift analyses available and doing a fit to the data using the K-G equation. This, to the best of our knowledge, has not been done. In fact, this research confirms these changes of pion-nucleus potential as one moves through the delta resonance. Furthermore, the data for 230 - 400 MeV reveal that pion real part of the potential is completely repulsive. The IST is based on extracting a number of points of the nuclear potential from available phase shifts using full Klein-Gordon equation for pion-nucleus systems. These extracted potential points are the most reliable in the exterior region, i.e. for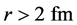
. The actual potential is then determined using these points as a guide. This potential, with its new analytical form, has been very successful in an analyzing pion-nucleus elastic scattering data in the low and delta resonance energy regions over the entire angles [18] -[20] for the elastic scattering of pions by 40Ca. In addition, it has been successful in analyzing the data of elastically scattered charged pions from 54Fe [21] . For charged pions, Coulomb effects are accounted for by implementing Stricker’s prescription [22] . Relativistic kinematic and parameter values are calculated by following Satchler’s treatment.
Although a variety of theoretical models have been used in the analyses of 
-nucleus data above the delta resonance [23] , only qualitative agreement between data and calculations was achieved [24] . In fact, in some cases, discrepancies between calculated elastic differential cross sections and data persist at forward angles; different models failed to account for the first diffraction minima in the measured elastic differential cross sections; and noticeable differences between calculations and data do exist at large angles. Most of the recent models used local optical potentials [25] [26] following Satchler’s method. These potentials are used in a Shrödinger equation obtained by reducing a truncated Klein-Gordon equation, i.e. neglecting 
term, and redefining its kinematical quantities. Coulomb potential 
was considered in its common form due to a uniformly charged sphere of radius
. Here, we’ll follow Satchler’s treatment, but with the inclusion of 
term, we use Stricker’s prescription to substitute for
.
In addition to analyzing the elastic scattering data, we calculate the reaction cross section and compare it with data. This provides another check to the nature of absorption.
In the subsequent sections, theory, results and discussion, and conclusions are presented.
2. Theory
The IST used, as a guide, to extract the pion-carbon local optical potential, from available phase shifts and full K-G equation, is completely outlined in Ref. [18] , and will not be repeated here. This extracted potential is then inserted into K-G equation for spinless relativistic cases. The non-monotonic nature of the real part of the potential is generated by having two potential functions. Similarly, to determine the interplay between volume and surface absorption, one needs at least two functional forms. Thus, the analytical form of the radial part of the potential is given by
, (1)
For such a spherical symmetric potential, the radial part of K-G wave function, 
, satisfies the following equation:
, (2)
where Rnl(r) is the r times the radial part of the wave function for a spherical symmetric external potential. Also, in Equation (2), 
and 
are given by
, (3)
, (4)
In Equation (3), E and m are the effective pion energy and effective pion mass, respectively, calculated by following Satchler’s relativistic correction treatment as explained below, and c is the velocity of electro-magnetic wave in vacuum. 
is the complex pion-nucleus potential. The Coulomb potential 
is included as a constant according to Stricker’s prescription and not as a function of 
due to a uniformly charged sphere of radius
.
The elastic differential cross section is calculated by using the following relation:
, (5)
with 
is the total scattering amplitude at an angle 
in the center of mass system:
, (6)
where 
is the point Coulomb scattering amplitude, 
is the point Coulomb phase shift, 
is the complex nuclear phase shift, and 
is the Legendre polynomial.
In many previous studies, the 
term in (4) was neglected. In our recent studies [14] [18] , we showed that the inclusion of this term is important in accounting correctly for large-angle differential cross sections. The large angle data are particularly important in determining the uniqueness. The Coulomb part is considered by using Stricker’s treatment. It is determined by changing the effective pion’s incident energy by the Coulomb barrier height, which is 
in this case, calculated from the relation:
, (7)
where 
is the target’s atomic number, 
, and 
is the effective Coulomb radius. The negative and positive signs are for 
and
, respectively.
As a further test to the correctness of our potential, the reaction cross section 
was calculated using:
, (8)
where 
is the S-matrix.
The kinetic energy, 
, in Equation (2) is in the center of mass system, whereas the experimental kinetic energies, 
, are given in laboratory system. We use the Satchler prescription to transform 
to the center of mass as done in the most theoretical treatments. The method relies on transforming the true pion mass 
and the pion bombarding energy in the laboratory system 
to the effective mass of the incident pion 
and the actual beam energy 
where 
is the target mass. Satchler’s treatment, followed by several authors, is summarized as follows:
The center-of-mass kinetic energy, 
, is defined as
, (9)
where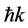 
is the relativistically correct center-of-mass momentum of the pion, and 
is the reduced mass of the two interacting particles:
, (10)
where the effective mass of the incident pion 
is defined as
, (11)
with 
where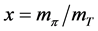 
and 
with
. In Equation (7), 
is given by:
, (12)
In atomic mass units
, one can use 
and 
for
. With this, one can rewrite Equation (9) as,
, (13)
Substituting Equations (10) and (12) in Equation (13), 
can be easily calculated.
3. Results and Discussion
The success of our potential, in describing the elastic scattering of charged pions from calcium isotopes and 54Fe at 180 MeV which lies in the delta resonance region of pions, forms a strong motivation for using its functional form to analyze pion-carbon elastic scattering data. This is because, so far, no potential has been capable of explaining 
large angle data, and the nature of the real part of the potential has been long remained controversial [26] . We start by analyzing 
elastic scattering data at 162 MeV where differential cross sections and phase shift analyses are available for both positive and negative pions. Our analyses establish that the non-Coulomb part for both 
and 
is the same at this energy. Then, we extend the analysis to two nearby energies also atop the resonance region, namely 150 and 180 MeV. In addition, and to test the capability of our potential, we continued the analysis at energies below and above the delta resonance, namely 120, 200, 230, 260, 280 and 400 MeV. As pointed out in our recent work [20] [21] , the parameters of our potential are modified so that both its real and imaginary parts match in the exterior region reasonably well, with the potential points obtained by the IST using available phase shifts and full K-G equation. These potential parameters, used for describing the experimental data successfully, are presented in Table 1.
As noted earlier, we first analyze the data at 162 MeV, which is in the 
-resonance region and the data for both 
elastic scattering are available. To fit both 
data at the same energy, with the same potential parameters, is an extra-constrain on the parameters search which determined our choice of the potential at this energy. We also provide the reaction cross-section data for both cases at this energy. Unfortunately no data are available.
Using the available phase shifts, we first determine the dotted points in Figure 1 using IST. These points should be quite good to determine the exterior part of the potential e.g. potential at
. The parameters of the potential are then determined to reproduce the external points reasonably well. The final parameters set, noted in Table 1, is then obtained from fitting the differential cross section which, as shown in Figure 1, is very good. In particular, both minima are well reproduced. The calculated reaction cross sections, 
, shown in Table 1 are in excellent agreement with the available data.
Next, we analyze the data for 
scattering at 150 MeV for which the phase shift analysis is available. The data also extend to 150˚ i.e. there is some information on back angle scattering. The determined potential from IST as well as the fit to the differential cross section are shown in Figure 2. Both the fits to the differential cross section and the calculated reaction cross section, noted in Table 1, are very good.
Unfortunately at the three nearby energies, namely 120, 180 and 200 MeV, no phase shift analyses are available. As such, these data are analyzed using the potential parameters determined for 150 and 162 MeV as guides. The potential parameters used, along with reaction cross sections, are listed in Table 1. The corresponding potentials, real and imaginary parts, with calculated and measured differential cross sections are shown in Figures 3-5 for 120, 180 and 200 MeV, respectively. In all these cases, the calculations reproduce quite well data at backward angles as well as the reaction cross sections. In particular, large-angle differential cross section data has been explained very well. To the best of our knowledge, no other potential has been successful in explaining these large-angle data.
Turning to the elastic scattering data on 
at 230, 260 and 280 MeV, there is a sudden change in the pattern of the differential cross section – it seems that the second minimum gradually is disappearing with increasing energy and the cross sections fall off smoothly. Unfortunately, there are no data at large angles. This change
Figure 1. The left two figures indicate the analytical form of our potential, its real and imaginary parts as solid lines and compare them to the extracted potential points obtained using IST from available phase shifts [27] . The right most figure shows the excellent agreement between calculated and measured elastic differential cross sections [28] , for 
at 162 MeV.
Figure 2. Same as Figure 1 but for 
at 150 MeV. Data are from Binon et al. [29] .
in pattern is reflected in the potential points determined using IST for 230 MeV incident energy shown in Figure 6. The real part of the potential in the interior is turning repulsive. This is a crucial result of the IST and leaves no possibility that the real part could be attractive. Also the repulsive nature of the real part is particularly pronounced at 260 and 280 MeV as shown in Figure 7 and Figure 8. At all these energies, the calculated reaction cross sections are in excellent agreement with the observed ones.
Figure 3. Same as Figure 1 but for 120 MeV incident energy. No phase shift analysis is available and hence, there are no dots or empty triangles in the figure at left.
Figure 4. Same as Figure 3 but for 180 MeV incident energy.
We particularly draw the attention to the IST-determined points in the region
. They clearly indicate the repulsive nature of the real part of the potential at 230 MeV. To examine further the nature of potential at higher energies, we fit the elastic differential cross sections at 260 and 280 MeV. As phase shift analyses are not available, we fit the data by adjusting the potential parameters used for the 230 MeV case. The potentials used, with their adjusted parameters shown in Table 1, have been very successful in explaining the elastic differential cross sections and in accounting for reaction cross sections. These potentials, with their real and imaginary
Figure 5. Same as Figure 3 but for 200 MeV incident energy.
parts, as well as the experimental and theoretical angular distributions, are drawn in Figure 7 and Figure 8. It is clear that our results support previous results indicating that the real parts of the potentials change from attractive to repulsive after 200 MeV [11] [26] [30] . On the otherhand we disagree with the theoretical results, which gave an acceptable estimate of angular distributions but not an excellent one, reported by Safari [31] indicating that the real part is repulsive even at 150 MeV for negative pions scattered from 12C target.
To test the capability of our potential in accounting nicely for angular distributions and in obtaining correct reaction cross sections at higher energies i.e., above the first nucleonic resonance but below the second one, we have chosen the 400 MeV case where measured elastic differential cross sections and reaction cross section are available. The potential parameters, along with reaction cross sections, are listed in Table 1. The potential, with its real and imaginary parts, and the calculated differential cross sections compared to the experimental ones are presented in Figure 9. Although the data are available only up to 60˚ in angular distribution, the fits as well as the calculated and observed reaction cross sections for 
are in excellent agreement.
Our potential (1) used herein and for calcium target [14] [21] differ from the one proposed by Satchler who only used the first term of the real part. The addition of the second term with strength parameter 
is dictated by the IST extracted potential points in the exterior region. The interplay between 
an 
determine the overall nature of the potential. The values of 
and its change from negative to positive at 230 MeV, with a small radius 
(approximately half the Coulomb radius
) and relatively small diffuseness parameter
, played an important role in shaping the potentials for all energies considered herein. The third and fourth terms in (1) represent, respectively, volume and surface absorptions. Since 
in all but 400 MeV case, one can conclude that most of absorptions are taking place at the surface of 12C, peaked around about 2.2 fm which is smaller than 
by 0.34 fm which may be considered an approximate value of the skin depth of the 12C-nucleus. This is reflected in all but the last figure. Thus, only a small fraction of pion flux reaches the interior of 12C for all but the 400 MeV case. This is, of course, expected since pions will interact strongly by nucleons near the surface, and will not penetrate to the interior at least at these energies. The variation of the values of the parameters further substantiates this simple physics. In the 400 MeV case, the absorption occurs throughout the volume but the repulsive nature of the real part again allows a fraction of the flux to penetrate.
Figure 9. Same as Figure 3 but for 400 MeV. Data are from Kahrimanis et al. [24] .
Looking at Table 1, it is clear that
, 
and except for the 400 MeV, 
and except for the 162 and 400 MeV cases, 
which, in effect, determine the slope of the potential are unchanged.
, 
and 
are also unchanged except for the 120 and 400 MeV, 120 and 400 and 230 MeV cases, respectively. Thus in the energy range considered herein the strength parameters vary substantially. The overall strength of the real part is monotonic below the
–resonance but its strength reduces atop the resonance turning repulsive after the resonance, at near 230 MeV. The strength and width of 
which is primarily responsible for surface absorption follow roughly the variation of the magnitudes of reaction cross section with energy. The latter increases from the incident at below 
-resonance, achieving maxima atop the resonance and then decline in its value. It seems that the effect of the 
-resonance becomes weak around 230 MeV.
4. Conclusions
As the case for 40Ca target, we demonstrate that the nuclear part of pion-12C potential is the same for positive and negative pions. We establish that local optical potential in conjunction with the KG equation can suitably explain the elastic scattering as well as reaction cross sections. We further note:
a) the strength and success of IST in predicting the potential points used as a guide for constructing the correct pion-nucleus potential. This is evident here in obtaining the nature of the potential, and in particular for the time establishing the repulsive nature of the real part at 230 MeV rather definitely. Such a change in the nature of the real part was very crucial in obtaining the correct differential and reaction cross sections.
b) the simple prescription of Stricker, in substituting for Coulomb effects, is effective for a nucleus as light as 12C.
c) the importance of the inclusion of 
term in the treatment, i. e. the full K-G equation, along with reliable large angle data and data on reaction cross sections in reducing the ambiguities in the parameter values that appeared in Hong et al.’s, Satchler’s and Akhter et al.’s works.
d) the skin depth of the 12C-nucleus is approximately 0.34 fm.
This investigation clearly establishes the importance of supplementing Satchler’s potential by the second term in (1). Our potential accounts nicely for all experimental values in the whole angular range and at all energies under consideration. It also confirms that pion elastic scattering is dominated by surface absorption whose relation to pion-nucleon scattering would be important to understand.
To the best of our knowledge, all other potentials showed a limited success in giving a general description of pion elastic scattering. As such, this investigation was a timely one to rectify the remedies of previous works. In fact, it provides an important methodology to determine potentials for describing elastic scattering data for scattered charged pions from 12C and other nuclei.
Acknowledgements
We acknowledge the financial support of the Deanship of Scientific Research at Taif University, Taif, Saudi Arabia for this investigation. The author also thanks Prof. F. B. Malik for fruitful discussions and his exceptional efforts in reading the revised version of the manuscript carefully.