Derivative of a Determinant with Respect to an Eigenvalue in the Modified Cholesky Decomposition of a Symmetric Matrix, with Applications to Nonlinear Analysis ()
1. Introduction
The increasing complexity of computational mechanics has created a need to go beyond linear analysis into the realm of nonlinear problems. Nonlinear finite-element methods commonly employ incremental techniques involving local linearization, with examples including load-increment methods, displacement-increment methods, and arc-length methods. Arc-length methods, which seek to eliminate the drawbacks of load-increment methods by choosing an optimal arc-length, are effective at identifying equilibrium paths including singular points.
In previous work [1] , we proposed a formula for the derivative of a determinant with respect to an eigenvalue, based on the trace theorem and the expression for the inverse of the coefficient matrix arising in the conjugate-gradient method. In subsequent work [2] -[4] , we demonstrated that this formula is particularly effective when applied to methods of eigenvalue analysis. However, the formula as proposed in these works was intended for use with iterative linear-algebra methods, such as the conjugate-gradient method, and could not be applied to direct methods such as the modified Cholesky decomposition. This limitation was addressed in Reference [5] , in which, by considering the equations that arise in the conjugate-gradient method, we applied our technique to the LDU decomposition of a nonsymmetric matrix (a characteristic example of a direct solution method) and presented algorithms for differentiating determinants of both dense and banded matrices with respect to eigenvalues.
In the present paper, we propose a formula for the derivative of a determinant with respect to an eigenvalue in the modified Cholesky decomposition of a symmetric matrix. In addition, we apply our formula to the arc-length method (a characteristic example of a solution method for nonlinear finite-element methods) and discuss methods for determining singular points, such as bifurcation points and limit points. When the sign of the derivative of the determinant changes, we may use techniques such as the bisection method to narrow the interval within which the sign changes and thus pinpoint singular values. In addition, solutions obtained via the Newton-Raphson method vary with the derivative of the determinant, and this allows our proposed formula to be used to set the increment. The fact that the increment in the arc length (or other quantities) may thus be determined automatically allows us to reduce the number of basic parameters exerting a significant impact on a nonlinear finite-element method. Our proposed method is applicable to the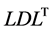 
decomposition of dense matrices, as well as to the 
decomposition of banded matrices, which afford a significant reduction in memory requirements compared to dense matrices. In what follows, we first discuss the theoretical foundations of our proposed method and present algorithms and programs that implement it. Then, we assess the effectiveness of our proposed method by applying it to a series of numerical experiments on a three-dimensional truss structure.
2. Derivative of a Determinant with Respect to an Eigenvalue in the Modified Cholesky Decomposition
The derivation presented in this section proceeds in analogy to that discussed in Reference 5. The eigenvalue problem may be expressed as follows. If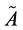 
is a real-valued symmetric 
matrix (specifically, the tangent stiffness matrix of a finite-element analysis), then the standard eigenvalue problem takes the form
, (1)
where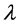 
and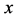 
denote the eigenvalue and eigenvector, respectively. In order for equation (1) to have trivial solutions, the matrix 
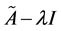must be singular, i.e.,
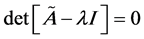. (2)
We will use the notation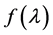 
for the left-hand side of this equation:
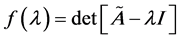. (3)
Applying the trace theorem, we find
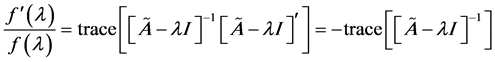, (4)
where
. (5)
In the case of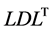 
decomposition, we have
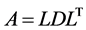(6)
with factors L and D of the form
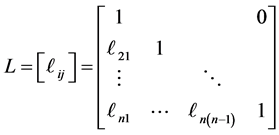, (7)
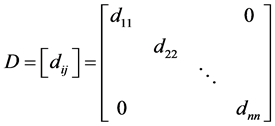. (8)
The matrix 
has the form
. (9)
Expanding the relation 
(where 
is the identity matrix) and collecting terms, we find
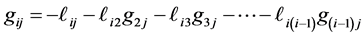. (10)
Equation (10) indicates that 
must be computed for all matrix elements; however, for matrix elements outside the bandwidth, we have
, and thus the computation requires only elements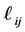 
within the bandwidth. This implies that a narrower bandwidth gives a greater reduction in computation time.
From equation (4), we see that evaluating the derivative of a determinant requires only the diagonal elements of the inverse matrix (6). Upon expanding the product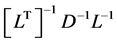 
using equations (7-9) and summing the diagonal elements, equation (4) takes the form
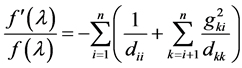. (11)
This equation demonstrates that the derivative of the determinant may be computed from the elements of the inverses of the matrices D and L obtained from the modified Cholesky decomposition. As noted above, only matrix elements within the a certain bandwidth of the diagonal are needed for this computation, and thus computations even for dense matrices may be carried out as if the matrices were banded. Because of this, we expect dense matrices not to require significantly more computation time than banded matrices.
By augmenting an 
decomposition program with an additional routine (which simply adds one additional vector), we easily obtain a program for evaluating the quantity
. The value of this quantity may be put to effective use in Newton-Raphson approaches to the numerical analysis of bifurcation points and limit points in problems such as large-deflection elastoplastic finite-element analysis. Our proposed method is easily implemented as a minor additional step in the process of solving simultaneous linear equations.
3. Algorithms Implementing the Proposed Method
3.1. Algorithm for Dense Matrices
We first present an algorithm for dense matrices. The arrays and variables appearing in this algorithm are as follows.
1) Computation of the modified Cholesky decomposition of a matrix together with its derivative with respect to an eigenvalue
(1) Input data A : given symmetric coefficient matrix,2-dimension array as A(n,n)
b : work vector, 1-dimension array as b(n)
n : given order of matrix A and vector b eps : parameter to check singularity of the matrix output
(2) Output data A : L matrix and D matrix, 2-dimension array as A(n,n)
fd : differentiation of determinant
ichg : numbers of minus element of diagonal matrix D (numbers of eigenvalue)
ierr : error code
=0, for normal execution
=1, for singularity
(3) LDLT decomposition
ichg=0
do i=1,n
do k=1,i-1
A(i,i)=A(i,i)-A(k,k)*A(i,k)２
end do
if (A(i,i)<0) ichg=ichg+1
if (abs(A(i,i))
ierr=1
return
end if
do j=i+1,n
do k=1,i-1
A(j,i)=A(j,i)-A(j,k)*A(k,k)*A(i,k)
end do
A(j,i)=A(j,i)/A(i,i)
end do
end do
ierr=0
(4) Derivative of a determinant with respect to an eigenvalue (fd)
fd=0
do i=1,n
<(i,i).
fd=fd-1/A(i,i)
<(i,j)>
do j=i+1,n
b(j)=-A(j,i)
do k=1,j-i-1
b(j)=b(j)-A(j,i+k)*b(i+k)
end do
fd=fd-b(j)２/A(j,j)
end do
end do 2) Calculation of the solution
(1) Input data A : L matrix and D matrix, 2-dimension array as A(n,n)
b : given right hand side vector, 1-dimension array as b(n)
n : given order of matrix A and vector b
(2) Output data
b : work and solution vector, 1-dimension array
(3) Forward substitution
do i=1,n
do j=i+1,n
b(j)=b(j)-A(j,i)*b(i)
end do
end do
(4) Backward substitution
do i=1,n
b(i)=b(i)/A(i,i)
end do
do i=1,n
ii=n-i+1
do j=1,ii-1
b(j)=b(j)-A(ii,j)*b(ii)
end do
end do
3.2. Algorithm for Banded Matrices
We next present an algorithm for banded matrices. The banded matrices considered here are depicted schematically in Figure 1. In what follows,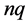 
denotes the bandwidth including the diagonal elements.
1) Computation of the modified Cholesky decomposition of a matrix together with its derivative with respect to an eigenvalue
(1) Input data A : given coefficient band matrix, 2-dimension array as A(n,nq)
b : work vector, 1-dimension array as b(n)
n : given order of matrix A
nq : given half band width of matrix A
eps : parameter to check singularity of the matrix
(2) Output data
A : L matrix and D matrix, 2-dimension array
fd : differential of determinant
ichg : numbers of minus element of diagonal matrix D (numbers of eigenvalue)
ierr : error code
=0, for normal execution
=1, for singularity
(3) LDLT decomposition
ichg=0
do i=1,n
do j=max(1,i-nq+1),i-1
A(i,nq)=A(i,nq) -A(j,nq)*A(i,nq+j-i)２
end do
if (A(i,nq)<0) ichg=ichg+1
if (abs(A(i,nq))
ierr=1
return
end if
do j=i+1,min(i+nq-1,n)
aa=A(j,nq+i-j)
do k=max(1,j-nq+1),i-1
aa=aaA(i,nq+k-i)*A(k,nq)*A(j,nq+k-j)
end do
A(j,nq+i-j)=aa/A(i,nq)
end do
end do
ierr=0
(4) Derivative of a determinant with respect to an eigenvalue (fd)
fd=0
do i=1,n
<(i,i)>
fd=fd-1/A(i,nq)
<(i,j)>
do j=i+1,min(i+nq-1,n)
b(j)=-A(j,nq-(j-i))
do k=1,j-i-1
b(j)=b(j)-A(j,nq-(j-i)+k)*b(i+k)
end do
fd=fd-b(j)２/A(j,nq)
end do
do j=i+nq,n
b(j)=0
do k=1,nq-1
b(j)=b(j)-A(j,k)*b(j-nq+k)
end do
fd=fd-b(j)２/A(j,nq)
end do
end do 2) Calculation of the solution
(1) Input data
A : given decomposed coefficient band matrix,2-dimension array as A(n,nq)
b : given right hand side vector, 1-dimension array as b(n)
n : given order of matrix A and vector b
nq : given half band width of matrix A
(2) Output data
b : solution vector, 1-dimension array
(3) Forward substitution
do i=1,n
do j=max(1,i-nq+1),i-1
b(i)=b(i)-A(i,nq+j-i)*b(j)
end do
end do
(4) Backward substitution
do i=1,n
ii=n-i+1
b(ii)=b(ii)/A(ii,nq)
do j=ii+1,min(n,ii+nq-1)
b(ii)=b(ii)-A(j,nq+ii-j)*b(j)
end do
end do
4. Numerical Experiments
To demonstrate the effectiveness of the derivative of a determinant in the context of 
decompositions in