L-Stable Block Hybrid Second Derivative Algorithm for Parabolic Partial Differential Equations

Fidele Fouogang Ngwane, Samuel Nemsefor Jator

Department of Mathematics and Statistics, Austin Peay State University, Clarksville, USA.
Department of Mathematics, USC Salkehatchie, Allendale, USA.

DOI: 10.4236/ajcm.2014.42008                

Abstract

An L-stable block method based on hybrid second derivative algorithm (BHSDA) is provided by a continuous second derivative method that is defined for all values of the independent variable and applied to parabolic partial differential equations (PDEs). The use of the BHSDA to solve PDEs is facilitated by the method of lines which involves making an approximation to the space derivatives, and hence reducing the problem to that of solving a time-dependent system of first order initial value ordinary differential equations. The stability properties of the method is examined and some numerical results presented.

Keywords

Hybrid Second Derivative Method; Off-Step Point; Parabolic; Partial Differential Equations

1. Introduction

We adopt the method of lines approach which is commonly used for solving time-dependent partial differential equations (PDE), whereby the spatial derivatives are replaced by finite difference approximations (see Lambert [1] , Ramos and Vigo-Aguiar [2] , Brugnano and Trigiante [3] , Cash [4] , Enright [5] , Hairer et al. [6] , Henrici [7] , Butcher [8] , Fatunla [9] , Jator [10] , and Onumanyi et al. [11] , [12] ). Consider the PDE of the form

(1)

subject to the initial/boundary conditions

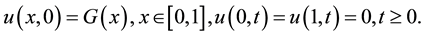(2)

We seek a solution in the strip by first fixing the grid in the spatial variable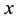, then approximating this spatial derivative using the central difference method, and finally solving the resulting system of first order time dependent ODEs. Specifically, we discretize the space variable with mesh spacings ,

.

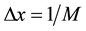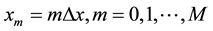We then define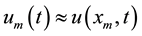, , and replace the partial derivatives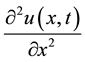

occurring in (1) by the central difference approximation to obtain

;, which reduces the PDE to the semi-

discrete problem

which can be written in the form

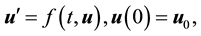(3)

where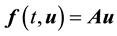, and A is an 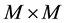matrix arising from the central difference approximations to the derivatives of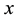. The problem (2) is now a system of first order ODEs which is solved by the BHSDA.

The paper is organized as follows. In Section 2, we derive a continuous approximation which is used to obtain the BHSDA. The BHSDA is also analyzed in section 2. The computational aspects of the method is given in Section 3. Numerical examples are given in Section 4 to show the accuracy of the method. Finally, the conclusion of the paper is discussed in Section 5.

2. Development of the method

We begin by considering a scalar form of (3)

(4)

where we assume that the function f is Lipshitz continuous and the problem (4) possesses a unique solution. Furthermore, let be an approximation of the theoretical solution at. Our objective is to simultaneously seek numerical approximations at the points and respectively, where is the step size, the grid index, and This approximation is provided by a continuous approximation as a by-product. Thus, we assume that is of the form

(5)

where are unknown coefficients.

In order to uniquely determine the unknown coefficients, we impose that the interpolating function (4) coincides with the analytical solution at the end point and also satisfies the differential Equation (3) at the points to obtain the following system of equations:

(6)

We note that (6) leads to a system of five equations which is solved by Cramer's Rule to obtain. The continuous method is constructed by substituting the values of into Equation (5) which is simplified and expressed in the form

(7)

where, , , , are continuous coefficients, and. The continuous

method (7) is then evaluated at, for to yield

(8)

Remark 2.1 In order to conveniently analyze and implement the method (8), we will express it in block form as given in (9).

(9)

where, , , , ,

, , and the matrices, , , , are 2 by 2 matrices whose entries are given by the coefficients of (8).

2.1. Local Truncation Error

Define the local truncation error of (4) as

(10)

where

, , ,

, and is a linear difference

operator. Assuming that is sufficiently differentiable, we can expand the terms in (10) as a Taylor series about the point to obtain the expression for the local truncation error., hence the

method is of order four.

2.2. Stability

Proposition 2.2 The BHSDA (9) applied to the test equations and yields.

(11)

with the amplification matrix

(12)

Remark 2.3 The dominant eigenvalue of specified by is a rational

function called the stability function which determines the stability of the method.

Proof. We begin by applying (2) to the test equations and which are expressed as and respectively; letting, we obtain a system of linear equations which is used to solve for with (12) as a consequence.

Definition 2.4 The block method (9) is said to be 1) -stable if for all, has a dominant eigenvalue such that; moreover, since is a rational function, the real part of the zeros of must be negative, while the real part of the poles of must be positive; 2) -stable if it is -stable and as.

Corollary 2.5 The method (9) is -stable and -stable.

Proof: The dominant eigenvalue for the method (9) is given by and the

proof follows from definition 2.4.

Remark 2.6 The stability region for the method (9) is given in Figure 1 showing the zeros and poles of the dominant eigenvalue.

3. Computational Aspects

The resulting system of ODEs (3) is then solved on the partition

is a constant step-size of the partition of, , is a positive integer and

the grid index.

Step 1: Use the block method (9) to solve (3) on rectangles,.

Step 2: Let, noting that, then for, ,

and, the approximations are simultaneously obtained on.

Step 3: Step 2 is repeated for, , and, to generate the approxi-

mations on.

We note that for linear problems, we solve (3) directly with our Mathematica code enhanced by the feature.

4. Numerical examples

Computations were carried out in Mathematica 9.0 and the errors were calculated as, where. We note that the method is particularly useful, but not limited to solving parabolic partial differential equations where the solution decays very rapidly and where the PDEs are stiff parabolic equations (see Cash [4] ).

Example 4.1 As our first test example, we solve the given PDE (see Cash [4] )

The exact solution.

In Table 1, it is noticed that the method with the BHSDA is the most accurate.

Example 4.2 As our second test example, we solve the given stiff parabolic equation (see Cash [4] )

The exact solution.

Cash [4] notes that as increases, equations of the type given in example 4.2 exhibit characteristics similar to model stiff equations. Hence, the methods such as the Crank-Nicolson method which are not -stable are expected to perform poorly. The BHSDA is -stable and perform excellently when applied to this problem. Therefore the BHSDA is competitive with the -stable methods of Cash [4] . In Table 2, we display the results for and a range of values for.

Figure 1. The region of absolute stability of the BHSDA of order 4 is to the left of the dividing line and is symmetric about the real axis; the square and plus symbols to the left and right of the imaginary axis represent the zeros and poles of q_max respectively.

Table 1. A comparison of errors of methods for Example 4.1 at t = 1.

Table 2. A comparison of errors of methods for Example 4.1 at t = 1 and ω = 1, Δx = 0.1, Δt = 0.1.

5. Conclusion

We have proposed a BHSDA for solving parabolic PDEs via the method of lines. The method is shown to be - stable and competitive with existing methods in the literature.

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Lambert, J.D. (1991) Numerical Methods for Ordinary Differential Systems. John Wiley, New York.
[2]	Vigo-Aguiar, J. and Ramos, H. (2007) A family of A-Stable Collocation Methods of Higher Order for Initial-Value Problems. IMA Journal of Numerical Analysis, 27, 798-817. http://dx.doi.org/10.1093/imanum/drl040
[3]	Brugnano, L. and Trigiante, D. (1998) Solving Differential Problems by Multistep Initial and Boundary Value Methods. Gordon and Breach Science Publishers, Amsterdam.
[4]	Cash, J.R. (1984) Two New Finite Difference Schemes for Parabolic Equations. SIAM Journal of Numerical Analysis, 21, 433-446. http://dx.doi.org/10.1137/0721032
[5]	Enright, W.H. (2000) Continuous Numerical Methods for ODEs with Defect Control. Journal of Computational and Applied Mathematics, 125, 159-170. http://dx.doi.org/10.1016/S0377-0427(00)00466-0
[6]	Hairer, E. and Wanner, G. (1996) Solving Ordinary Differential Equations II. Springer, New York. http://dx.doi.org/10.1007/978-3-642-05221-7
[7]	Henrici, P. (1962) Discrete Variable Methods in ODEs. John Wiley, New York.
[8]	Butcher, J.C. (1987) The Numerical Analysis of Ordinary Differential Equations, Runge-Kutta and General Linear Methods. Wiley, New York.
[9]	Fatunla, S.O. (1991) Block Methods for Second Order IVPs. International Journal of Computational Mathematics, 41, 55-63. http://dx.doi.org/10.1080/00207169108804026
[10]	Jator, S.N. (2010) On the Hybrid Method with Three-Off Step Points for Initial Value Problems. International Journal of Mathematical Education in Science and Technology, 41, 110-118 http://dx.doi.org/10.1080/00207390903189203
[11]	Onumanyi, P., Sirisena, U.W. and Jator, S.N. (1999) Continuous Finite Difference Approximations for Solving Differential Equations. International Journal of Computational Mathematics, 72, 15-27. http://dx.doi.org/10.1080/00207169908804831
[12]	Onumanyi, P., Awoyemi, D.O., Jator, S.N. and Sirisena, U.W. (1994) New Linear Mutlistep Methods with Continuous Coefficients for First Order Initial Value Problems. Journal of the Nigerian Mathematics Society, 37-51.