1. Introduction
In an article published in World Journal of Mechanics [1], I suggested new ideas to explain the mechanical behaviour of macroscopic rigid bodies exposed to simultaneous non-coaxial rotations. In that paper, I proposed new dynamic hypotheses and a new mathematical model to represent the dynamics of systems under simultaneous rotations, based on a rational interpretation of the superposition of movements. For this purpose, I analysed velocity and acceleration fields that are generated in an object with intrinsic angular momentum, and assessed new criteria for coupling velocities.
I conducted various experiments which confirmed the theory proposed. The experiments have been analysed and explained in a video accompanying the referred paper: “New Dynamic Hypotheses” [2].
In May 2013, a new article in this journal was published, presented by the investigator Luis A. Pérez, with new experimental evidence confirming our thesis. In Luis A. Pérez’s article [3], the author corroborated the hypothesis of the Theory of Dynamics Interactions, by new experimental tests he designed.
An associated video with experiments was presented to support the discussion in the paper: Reflecting new evidences on Rotational Dynamics [4]. In this new video presented by the investigator Luis A. Pérez, new experimental tests are shown, which again confirm the proposed dynamic theory.
The author states: “I read the referred article with some scepticism... However, the subject was so interesting to me that I designed my own experimental tests with the purpose of achieving a clearer cut inertial mobile”. And he adds at the end of the video: …“The new dynamic hypotheses, proposed by Professor Gabriel Barceló, are thus empirically demonstrated”...
In this paper, we will discuss the laws of motion resulting from this model, and the reactions and inertial fields that cannot be explained by classical mechanics. We will first establish conceptual definitions and idealised models so as to deduce the Theory of Dynamic Interactions. We also put forward the principles and axioms from which the development of the conceptual structure of the TID starts. Consequently, we will develop the deduced laws of dynamic behaviour. These laws and the equation of the obtained movement can be used to predict the future behaviour of dynamic systems which up till now could be understood as chaotic. The laws also allow us the interpretation of certain phenomena of nature, such as the rings of Saturn or the own ecliptic of the solar system. And finally, we refer to the possibility of conceiving other laws of rotational dynamics if we start from other different dynamic hypotheses.
Numerous examples of these dynamic phenomena can be found in nature, such as the flight of the boomerang.
2. Definitions and Theoretical Models
For the deduction of the proposed laws, we start from the prevailing concepts and models of Classical Mechanics, such as for example the rigid solid, dynamic fields, and the notion of point in an isotropic and homogeneous space [5].
Moreover, to develop the dynamics of systems accelerated by sustained rotation, we will include other abstractions and theoretical models, specific for the rotational dynamics of dynamic interactions [6]. For the development of our reasoning, we state the following conceptual definitions.
2.1. Rotational Inertia
This is the tendency of bodies to maintain their previous rotational dynamic state around an axis, or rest.
When a rotation movement around a main inertia axis is applied to a revolving body or to a body with axial symmetry, it will initiate a rotation around that axis which will be maintained, turning on the same plane and around the same axis, unless new acting torques modify its dynamic state.
2.2. Angular Momentum
The magnitude defines the rotation movement of bodies. It is the product of its momentum of inertia by the angular rotation speed.
2.3. Intrinsic Angular Momentum
This is the angular momentum of a body with rotation, referring to its centre of mass and in a particular reference system.
In line with Landau and Lifshitz [7]: ... “The angular momentum M of a mechanical system is composed of its “intrinsic angular momentum” in a reference system in which it is in rest, and the angular momentum R × P due to its movement as a whole” [8].
2.4. Dynamic Balance
The state reached by bodies that have angular momentum, when they are subject to a constant, external non-axial torque, generating a recurring movement. If the initial rotation axis is symmetrical, a first external torque can be instant and not necessarily constant, maintaining the rotation around this main inertia axis indefinitely because of rotational inertia. The rotational inertia allows therefore that an instant action can have an unlimited effect in time. In absence of friction, the action of a constant external momentum on a revolving body, with a non-coaxial rotation, can generate a dynamic balance, also constant.
2.5. Dynamic Stability
The capacity of a body to maintain a constant balanced situation or dynamic permanence, especially in situations that can produce a change in its state.
It is an inertial characteristic of mass which causes a stabilising effect on bodies equipped with angular momentum, due to its rotational inertia.
2.6. Constant Turn
Said of the rotation movement of a system, or a body, when it has two points that are being kept in the same dynamic state in time. In this supposition, the system is in a state of “constant turn around a fixed axis”. Based on the concept of rotational inertia, it is easy to infer a dynamic model based on a constant turn.
2.7. Coupling of Movements
This is a dynamic characteristic by which, if several actions act on a mass, a final dynamic state is produced which is constituted by the algebra addition of the several actions, giving as a result the composition or superposetion of movements.
2.8. Orbital Movement
The movement of a body with intrinsic rotation, as the result of the coupling of its translation speed, with a velocities field generated by a second non-coaxial momentum. In case no translation speed is present, the dynamic reaction will be a change which we will call precession movement.
2.9. Dynamic Interactions
They are the reactions that are caused to bodies with intrinsic angular momentum when they are submitted to new non-coaxial momenta.
In line with the proposed dynamic model, dynamic interactions are produced in free bodies with rotation in space when they are provoked by certain stimuli which produce a characteristic and differentiated behaviour in respect to the one of bodies without intrinsic rotation.
2.10. Inertial Field
Said of the anisotropic accelerations field which is generated in a rotating body, when it is submitted to a noncoaxial momentum. We identify the inertial field as a torsion field, generating inertial forces created by the rotational movement itself.
2.11. Inertial Reactions
Said of the variation of the dynamic state of the rotating bodies, which is generated by the existence of angular momentum in the body.
2.12. Material Point Equipped with Inertial Mass and Orientation
To the idealised abstraction of the “point” of classical mechanics, inertial reactions are added due to its solidary situation with the rest of the system.
In mechanics, a “quantity of mass” is traditionally assigned to the idealised “point”. In our case, apart from this quantitive quality, we add the “inertial” nature of that mass, which limits and conditions its dynamic freedom. Its orientation will determine the direction of its inertial nature; the oriented point will be identified by an additional triad of unitarian orthogonal vector. In a Cartesian reference system, each oriented point of a rigid system will have nine spatial freedom degrees, apart from time.
The inertia and orientation of each point, and, being a rigid solid, its solidary action, will need to be taken into account when establishing the inertial reactions that are raised when a non-homogeneous velocities field appears determining a inertial field of velocities in the body, which we can identify by a field of inertial forces. This formulated model is necessary to determine the behaviour of a point of the rigid body, submitted to two simultaneous non-coaxial rotations.
3. Theory of Dynamic Interactions
Towards 1956, the scientist and professor Miguel Catalán [9] proposed us, his students, the existence of certain dynamic conjectures [10,11]. In his text books a possible correlation between the structure of an atom and rotational dynamics was explained [12]. These conjectures caused me a real scientific concern during many years.
I was also concerned about the fact that in nature, we usually find simultaneous movements of intrinsic rotation, orbit and precession. We did not have knowledge, in classical mechanics, of any mathematical model that established a scientific correlation between these movements when they occur simultaneously. Neither did we have knowledge of any type of joined analysis which determines possible inferences of one phenomenon on the others. Intuitively an aporia could be proposed stating that between the movements of orbit and rotation a physical correlation could exist which mathematical expression had not been revealed so far and as such the presently accepted laws of the behaviour of rotating bodies in space would turn out insufficient to exactly describe the real physical reality of rotating bodies.
With these questions in mind, we started an exhaustive historical study about classical rotational dynamics, to prove that studies initiated in the 19th C. had been subsequently forgotten [13]. As a result of this study, a book was published about the knowledge of classical rotational dynamics [10]:
Having observed nature and taken into account the deductions, we have reached the conclusion that the successive application of non-coaxial momenta on a rigid solid can cause to generate:
1. Non-homogeneous distributions of velocities and accelerations
2. Coexistence of non-coaxial rotations
Coupling of the distribution of the resulting velocities with the translation movement of the centre of the body’s masses
These hypotheses are differential criteria of the Theory of Dynamic Interactions which can be confirmed by experiments.
We start from the initial hypothesis that, in the supposition of simultaneous non coaxial rotations, fields of non-homogeneous velocities are produced in the rigid solid body. These fields with non-homogeneous distributions generate anisotropic accelerations fields. These fields can be interpreted as fields of inertial forces, created in space as an effect of simultaneous non-coaxial rotations, which generate inertial reactions. In classical mechanics, these inertial forces constitute a specific chapter that is unstructured in the rest of the discipline.
The coupling of the dynamic fields referred creates differentiated dynamic states which we can define as Dynamic Interactions.
It is our objective to define the dynamic laws of the behaviour of rigid solid bodies, when they are submitted to simultaneous multiple rotations. To achieve this, we have conceived the referred idealised theory models, such as, for instance, the solid with constant turn, or the material point equipped with inertial mass and orientation, which permit us to apply coherent abstractions in a systematic way.
From these dynamic hypotheses, multiple discriminating deductions can be obtained, which determine differentiated axioms. These axioms allow us to put forward the rotational dynamic theory of interactions.
3.1. Principles and Axioms
Based on the conjectures of Miguel Catalán, we developed the referred non-Newtonian hypotheses in rotational dynamics, whose mathematical formulation, allowed the design of a simulation programme to determine the behaviour of bodies in space. The conciliation of this simulation programme with reality permitted us to conceive a physical-mathematical model of dynamic interactions and consequently propose the axioms of non-Newtonian rotational dynamics and the resulting natural laws.
The rotational dynamics based on the hypotheses of inertial reactions is based on the principles of conservation of certain measurable magnitudes, such as the total mass, the angular momentum and the total energy.
Taking as a starting point those principles of conservation of measurable magnitudes, and the referred hypotheses deduced from the observation of the inertial reactions that are produced in nature, certain specific axioms can be established [14,15]:
1º. The rotation of space determines the generation of inertial fields.
2º. The inertial fields cause dynamic interactions.
3º. When a solid is subject to successive non-coaxial momenta, inertial fields are generated in the solid which are configured as non-homogeneous distributions of velocities and accelerations.
4º. When a solid with intrinsic rotation is submitted to a new non-coaxial external momentum, the generated field of velocities is coupled to the field of translation speeds.
5º. The action of successive non-coaxial momenta on a rigid body cannot be determined by aggregation or calculated by means of the resultant of the forces or/ and torques.
The third axiom specifies the two formulated before, assuming the generation of fields, generally anisotropic, in the supposition of bodies equipped with intrinsic rotation, when are stimulated by new non-coaxial torques. The fourth axiom formulates discriminating coupling of the velocities’ field, as opposed to the criteria admitted in classical mechanics since Poinsot [16]. The fifth axiom reminds us of the impossibility of the use of vector algebra for these phenomena.
From these axioms, the behaviour laws of bodies subject to non-coaxial successive momenta can be inferred, as well as behaviour laws of non-newtonian rotation dynamics of Dynamic Interactions.
3.2. Formulation
We will repeat the deductive analysis which will allow us to reach the definition of the proposed mathematical model: supposing a mobile in space with an initial translation speed  in its gravity centre, submitted to an instant momentum
in its gravity centre, submitted to an instant momentum 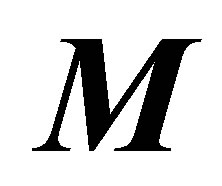 around a main inertia axis, generating because of its rotational inertia, a movement of constant turn with speed
around a main inertia axis, generating because of its rotational inertia, a movement of constant turn with speed . We suppose that the mobile has an inertia momentum I around this rotation axis and, therefore, has a constant angular momentum
. We suppose that the mobile has an inertia momentum I around this rotation axis and, therefore, has a constant angular momentum . When it is submitted to a new non coaxial momentum
. When it is submitted to a new non coaxial momentum  and due to the specific distribution of velocities and accelerations caused in rigid solid revolving bodies stimulated to realise successive intrinsic rotations around different axis, an inertial reaction will be generated, which we define as a field of dynamic interaction
and due to the specific distribution of velocities and accelerations caused in rigid solid revolving bodies stimulated to realise successive intrinsic rotations around different axis, an inertial reaction will be generated, which we define as a field of dynamic interaction , equivalent to an inertial torque (gyroscopic torque).
, equivalent to an inertial torque (gyroscopic torque).
Such field of dynamic interaction will be perpendicular to . Based on the Principle of Conservation of the Quantity of Movement, the resulting momentum will be equivalent to the acting external one:
. Based on the Principle of Conservation of the Quantity of Movement, the resulting momentum will be equivalent to the acting external one:
 (1)
(1)
Therefore, both will possess the same module which we determine with the equation:
 (2)
(2)
Because of the dynamic reaction which is caused by the action of the new non coaxial momentum , the mobile will obtain a precession speed
, the mobile will obtain a precession speed , defined by the scalar quotient:
, defined by the scalar quotient:
 (3)
(3)
Thus, we can infer that the field of inertial forces generated in the rotating space by a new non-coaxial torque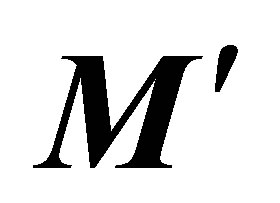 , on a mobile with rotation movement, and with inertia momentum I around this rotation axis, and therefore with a previous angular momentum
, on a mobile with rotation movement, and with inertia momentum I around this rotation axis, and therefore with a previous angular momentum , forcing the mobile to acquire a precession speed
, forcing the mobile to acquire a precession speed .
.
This precession speed can be coupled to the translation speed of the centre of masses , generating an orbital movement [14]. In such way, the path of the mobile will be defined by the successive velocities of the body
, generating an orbital movement [14]. In such way, the path of the mobile will be defined by the successive velocities of the body , determined by the matrix product of the rotational operator
, determined by the matrix product of the rotational operator  on the initial speed vector
on the initial speed vector , giving as a result the general equation of movement for bodies with angular momentum [1,6], when subject to successive non-coaxial torques:
, giving as a result the general equation of movement for bodies with angular momentum [1,6], when subject to successive non-coaxial torques:
 (4)
(4)
This supposes a rotation of the speed vector on the plane of the acting momentum  keeping its module constant. In this equation, the rotational operator
keeping its module constant. In this equation, the rotational operator  is the matrix that transforms the initial velocity into the one that corresponds to each successive dynamic state, by means of a rotation, being:
is the matrix that transforms the initial velocity into the one that corresponds to each successive dynamic state, by means of a rotation, being:
 (5)
(5)
As such we can observe how the rotational operator  is a function of the acting external torque
is a function of the acting external torque 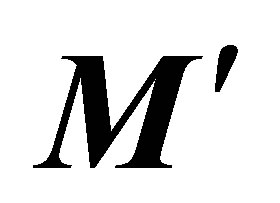 and of time t. There exists a clear relation between the angular velocity
and of time t. There exists a clear relation between the angular velocity  of the orbit, the acting torque
of the orbit, the acting torque  and the initial angular velocity
and the initial angular velocity  (Equation (2)). This precession speed
(Equation (2)). This precession speed  can be observed simultaneously with the initial
can be observed simultaneously with the initial  which is kept constant in the body. In such way, we obtain a simple mathematical relation between the angular velocity
which is kept constant in the body. In such way, we obtain a simple mathematical relation between the angular velocity  of the body and its translation velocity
of the body and its translation velocity . As a result, we can relate dynamic effects to the velocity and a clear mathematical correlation between rotation and translation.
. As a result, we can relate dynamic effects to the velocity and a clear mathematical correlation between rotation and translation.
3.3. Physical-Mathematical Model
From the obtained movement equation, a computer programme of simulation of dynamic behaviour was developed, coherent with the theory and prototypes were designed [1,6], for the realisation of experimental tests. Those tests confirmed the dynamic hypotheses proposed in the theory. As indicated in the introduction, other investigators have conducted other tests with equally positive results.
We are of the opinion that numerous examples can be offered to test these dynamic hypotheses which would allow us to interpret many suppositions of nature which up to date have not been fully understood, and more specifically, to confirm that the orbital path of a rigid solid demands the existence of an intrinsic rotation of the mobile [17].
The Theory of Dynamic Interactions that is put forward, justifies how a rigid solid with intrinsic rotation, when subject to a new non-coaxial external momentum, generates an orbital path. If the external momentum is kept constant, the movement will be recurrent in a closed path.
In the supposition of rigid solid bodies with axial symmetry or revolution, the action of external non-coaxial momenta can generate a dynamic balance.
In such a case of bodies with axial symmetry, we can propose a series of specific laws: Those laws are coherent with the described mathematical model where the rotational inertia allows a constant and balanced intrinsic rotation movement, and where no coupling of non-coaxial rotations is produced.
Based on the precedents mentioned above and following the behaviour of rigid solid bodies with axial symmetry, that turn around an axis with a point of support, in a field of forces in space, we can propose laws that, in our opinion, better justify the behaviour of bodies with axial symmetry, equipped with own rotation around a principal axis of its inertial ellipsoid.
All this allows us to conceive general laws for bodies with axial symmetry, in space and unattached, to interpret the behaviour of bodies with angular momentum and applicable as well in the case of a body submitted to attachments, which would be the case of a point of support with or without sliding.
4. Behaviour Laws of Bodies with Axial Symmetry
Starting from the developed axioms and in line with the deduced equation of movement, and the proposed physical-mathematical model, we will define now the Laws of rotational dynamics of rigid solid bodies with axial symmetry, when subject to successive non-coaxial momenta, or including for those same bodies when equipped with intrinsic angular momentum.
4.1. First Law
When a rigid body of axial symmetry is submitted to a rotation movement around a main inertia axis, it will maintain such rotation, even when the forces that generated it are interrupted.
This law which we can define as the Law of Conservation of rotation movement, though it could be identified with the principle of conservation of angular momentum, is also a consequence of the Principle of Inertia, when specifically interpreted in the area of rotational dynamics. In our field, the Principle of Inertia, should be interpreted, in the supposition of rigid solid bodies equipped with intrinsic rotation, in a sense that this rotation movement will be maintained, until some action is acting to modify its dynamic state. Therefore, priority has to be given to the inertia when looking at the reason for this peculiar behaviour of nature.
Based on this law, we can repeat the concept of Rotational Inertia, which would correspond with the inertia of the body when it is submitted to the rotation movement around a main axis of inertia, and leads us to state the first corollary: a body with axial symmetry will tend to maintain its rotation around the main axis of inertia, even if the forces acting upon it are interrupted, or will keep its resting state when there is absence of excitation (L1-C1).The concept of Rotational Inertia allows to justify the tendency of all rigid solid bodies with rotation, to keep on turning on the same plane and around the same axis (L1- C2).
In line with the above, we can propose the following definition: The rotational inertia of a rotating body is determined by the product of its mass by the square of its distance to the rotation axis and therefore, we will use the same measurement units as for the momentum of inertia (L1-C3).
Simultaneously, we can define the concept of Translational Inertia which would correspond to the inertia of a body, and as a result, when absence of external excitations, its centre of mass will maintain its resting state or the movement of uniform translation of the system (L1- C4).
Starting from the second proposed hypothesis, and if different rotations around different axis can be simultaneously generated on a body, we can infer that: In nature, mass permits different rotational inertia for a same body (L1-C5) in such a way that: each rotational inertia will generate a tendency to keep each rotation movement constant and independent (L1-C6). We can also define: the Rotational Invariance as a property of mass, where by, for bodies equipped with intrinsic rotation, a dynamic and energetic balance can be obtained, apparently immutable and constant, because of its inertial behaviour (L1-C7). And lastly: this characteristic of mass generates a rigidity in space, due to the rotational resistance of bodies equipped with angular momentum, this rotational invariance being an intrinsic characteristic, independent from any reference system (L1-C8).
4.2. Second Law
If on a solid body in space a torque, is acting with momentum , an accelerated rotation movement will be generated with velocity
, an accelerated rotation movement will be generated with velocity  and acceleration
and acceleration , around an axis coinciding with the torque; and if subsequently a new torque of momentum
, around an axis coinciding with the torque; and if subsequently a new torque of momentum , is acting, not coinciding with the direction of the first one, this new torque will generate a new movement of velocity rotation
, is acting, not coinciding with the direction of the first one, this new torque will generate a new movement of velocity rotation , around an axis perpendicular to the one of momentum
, around an axis perpendicular to the one of momentum .
.
Therefore, and in this supposition, the solid body is susceptible to movements of simultaneous rotation, but without their vector addition: no coupling of movements or vector composition of the resulting rotations is produced. As a corollary, we can propose that: Solid rigid bodies equipped with intrinsic angular momentum, subject to successive torques, do not comply with the classical principle of vector addition of movements (L2-C1).
It is also important to underline that the reaction of the mass to a same excitation is different in regard to the preexisting dynamic state (L2-C2) The external torque generates a rotation around the axis of the torque in the first case, and around another axis in the second case, always supposing that they are not coaxial.
4.3. Third Law
The rigid solid bodies equipped with intrinsic angular momentum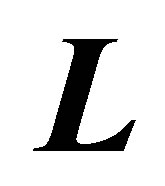 , with rotational velocity
, with rotational velocity , when submitted to a new momentum
, when submitted to a new momentum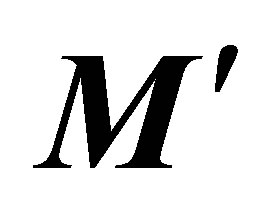 , constituted by two forces
, constituted by two forces , which are not spatially coinciding with the existing angular momentum, will be raised by an inertial reaction, which will generate a new rotation movement, not coinciding in space with
, which are not spatially coinciding with the existing angular momentum, will be raised by an inertial reaction, which will generate a new rotation movement, not coinciding in space with .
.
The dynamic behaviour of the observed body will be the result of its initial dynamic state, and of the inertial field of accelerations generated in the body by the second torque, due to the non-homogeneous distribution of velocities which generate a field of inertial forces equivalent to a momentum of dynamic interaction , orthogonal to the acting torque.
, orthogonal to the acting torque.
As a result of the above mentioned, we can propose that for rigid solid bodies with angular momentum , submitted to new non-coaxial momenta
, submitted to new non-coaxial momenta , the inertial reaction of mass can be interpreted as a mathematical operator that transforms this second applied momentum
, the inertial reaction of mass can be interpreted as a mathematical operator that transforms this second applied momentum , in another inertial one
, in another inertial one :
:
 (6)
(6)
Being:
 = Applied momentum
= Applied momentum
 = Resulting inertial momentum G = Inertial mathematical operator This operator G is a matrix which determines the inertial dynamic interaction that is produced in these suppositions in nature.
= Resulting inertial momentum G = Inertial mathematical operator This operator G is a matrix which determines the inertial dynamic interaction that is produced in these suppositions in nature.
4.4. Fourth Law
Rigid solid bodies equipped with intrinsic angular momentum , with rotation speed
, with rotation speed  and a linear initial speed of its centre of mass
and a linear initial speed of its centre of mass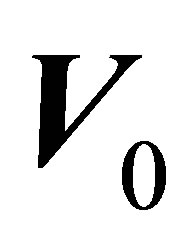 , when submitted to a new momentum
, when submitted to a new momentum , constituted by two forces
, constituted by two forces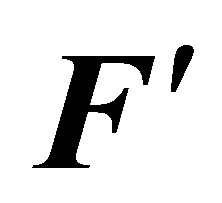 , not coinciding in direction with the existing angular momentum, will generate a movement of the body’s centre of mass in the direction of the momentum
, not coinciding in direction with the existing angular momentum, will generate a movement of the body’s centre of mass in the direction of the momentum .
.
In this case, the action of the forces  of the torque, on the solid will produce a displacement of the body’s centre of mass with a direction different to
of the torque, on the solid will produce a displacement of the body’s centre of mass with a direction different to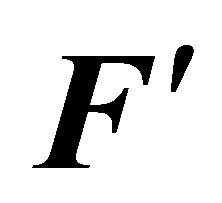 , instead of following its direction. The centre of gravity will effectively initiate a movement in the direction of
, instead of following its direction. The centre of gravity will effectively initiate a movement in the direction of , and not in the direction of the force.
, and not in the direction of the force.
As a first corollary we can propose that, rigid solid bodies equipped with intrinsic angular momentum, when submitted to successive non coaxial torques, will not comply with the principle of proportion between forces and accelerations (L4-C1).
To determine the equations of the resulting movement in this case, we will need to take into account the coupling that is produced in nature between the translation movement and the rotation movement generated by the second torque (L4-C2). We understand that, on the contrary, there will exist no coupling between the translation movement and the turn, due to the acting first torque (L4-C3).
And the following corollary: A solid body with intrinsic angular momentum and linear initial speed , when subject to a new torque of momentum
, when subject to a new torque of momentum , non-coaxial, will initiate a path of orbit around a new axis which can be external to the body itself (L4-C4).
, non-coaxial, will initiate a path of orbit around a new axis which can be external to the body itself (L4-C4).
4.5. Fifth Law
If the new torque of momentum  is constant in time, and the body equipped with intrinsic angular momentum, is moved with the linear initial velocity
is constant in time, and the body equipped with intrinsic angular momentum, is moved with the linear initial velocity , it will trace a movement of closed orbit with velocity
, it will trace a movement of closed orbit with velocity , maintaining its initial rotation movement with velocity
, maintaining its initial rotation movement with velocity , the orbitation movement stopping when the action of momentum
, the orbitation movement stopping when the action of momentum 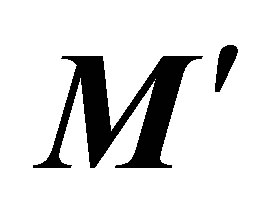 stops.
stops.
This behaviour has to be understood in line with the reaction that is caused on rigid solid bodies with angular momentum, due to its inertial behaviour when subject to a turn not coinciding in space with its angular momentum. These inertial reactions will modify in a selective way the path of the mobile, which will keep its initial rotation , but will modify its path when transforming the direction of the vector
, but will modify its path when transforming the direction of the vector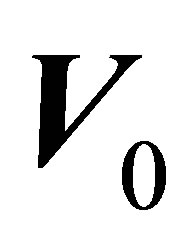 , keeping its module constant.
, keeping its module constant.
When mentioning that the momentum is kept constant, this has to be interpreted as a relation of interaction. Therefore, it will have to be constant in magnitude but also in orientation in respect to the intrinsic rotation axis of the body.
If the axis of the momentum of the second torque  coincides with the existing rotation axis, an angular acceleration will be generated in the body. This acceleration will be maintained while the torque is acting, disappearing with it, but in this case no inertial interaction behaviour will be produced.
coincides with the existing rotation axis, an angular acceleration will be generated in the body. This acceleration will be maintained while the torque is acting, disappearing with it, but in this case no inertial interaction behaviour will be produced.
As a first corollary, we can propose that in certain cases, when on a body with translation in space, two non-coaxial torque are acting successively, the first torque will generate a rotation movement around an axis coinciding with the one of the torque, but the second torque to act will generate an acceleration of the body in its translation movement because of the change of direction of vector , but not its module (L5-C1).
, but not its module (L5-C1).
The successive velocities of the body 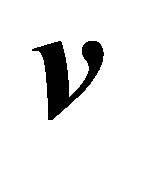 will be defined by the matrix product of the rotation operator
will be defined by the matrix product of the rotation operator 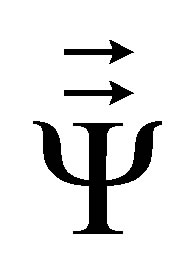 on the vector of initial velocity
on the vector of initial velocity , in line with the Equation (4), (L5-C2).
, in line with the Equation (4), (L5-C2).
In the case of an instant initial torque, and another constant subsequent one, but non-coaxial with the first one, the action of the second torque is an accelerated movement but only of change of orientation of the translation velocity: The result of these interactions is a dynamic balance between the second torque and the inertial reaction of dynamic interaction, (L5-C3).
However, in case both successive torques are coaxial, they will generate accelerated rotation around an axis coinciding with the one of momentum (L5-C4).
Therefore, we can propose as a new corollary that: The action of force  and therefore of momentum
and therefore of momentum , produces a constant orbital speed in module, instead of a constant linear acceleration as occurred in a body without intrinsic angular momentum (L5-C5). If the action of that new momentum
, produces a constant orbital speed in module, instead of a constant linear acceleration as occurred in a body without intrinsic angular momentum (L5-C5). If the action of that new momentum  is interrupted, then immediately the variation of the direction of the orbital speed will be stopped. However, it is necessary to note that the generated orbital movement supposes a variation of the path of the body’s centre of mass, maintaining the module of its velocity constant. If the new torque of momentum
is interrupted, then immediately the variation of the direction of the orbital speed will be stopped. However, it is necessary to note that the generated orbital movement supposes a variation of the path of the body’s centre of mass, maintaining the module of its velocity constant. If the new torque of momentum 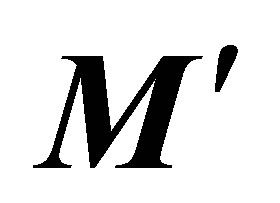 is maintained constant, as well as the angular rotation velocity
is maintained constant, as well as the angular rotation velocity , the new path will be a circumference which could be transformed in an ellipse, if the initial variables are not kept constant. In case these variables are kept constant, the path will be a circumference with as a radius the scalar quotient:
, the new path will be a circumference which could be transformed in an ellipse, if the initial variables are not kept constant. In case these variables are kept constant, the path will be a circumference with as a radius the scalar quotient:
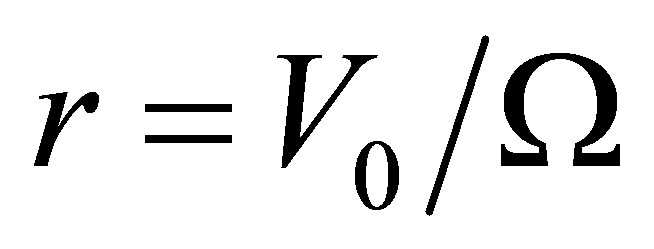 (7)
(7)
Being:
Ω = Module of the angular precession speed of the orbital movement, being its value the scalar quotient: 
V0 = Module of the linear initial velocity r = Radius of the path of the centre of mass.
4.6. Sixth Law
In bodies equipped with intrinsic angular momentum, when submitted to an action which supposes the variation in space of its angular momentum, no coupling is produced between the initial angular momentum  and its increase.
and its increase.
It should be noted that there will be no coupling if they are not coinciding spatially. As a first corollary, we can propose (L6-C1): For bodies equipped with intrinsic angular momentum, when submitted to a new torque of momentum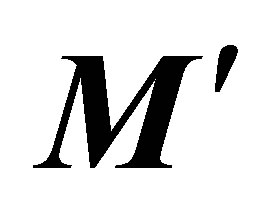 , not coinciding spatially, after a time DT, the increase of angular momentum
, not coinciding spatially, after a time DT, the increase of angular momentum  will not be vectorially added to the existing initial angular momentum L.
will not be vectorially added to the existing initial angular momentum L.
Being:  (8)
(8)
The vector addition of non-coaxial angular momenta is not possible. It can be understood as an inertial resistance of nature to modify the existing angular momentum (L6-C2).
4.7. Seventh Law
For bodies equipped with intrinsic angular momentum and linear velocity of its centre of mass, when submitted to an action which supposes the variation in space of its angular momentum, a coupling will be produced between the field of translation velocities and the field of velocities generated by the new action, thus creating a new orbital movement of angular velocity .
.
As a first corollary (L7-C1): If a non-coaxial torque is applied to a body equipped with translation and intrinsic angular momentum, an inertial interaction will be generated because of the coupling between the increase of the quantity of angular momentum, due to the new torque, and the kinetic momentum of the existing translation.
This dynamic interaction which is caused to a body equipped with intrinsic angular momentum, is an inertial but effective reaction and therefore its action cannot be neglected or forgotten. The produced inertial reaction will modify the body’s path by means of an orbit with angular velocity , in such a way that the value of its module will correspond to the quotient of the following scalar values:
, in such a way that the value of its module will correspond to the quotient of the following scalar values:
 (9)
(9)
As a second corollary (L7-C2): If a body with intrinsic angular momentum is twisted with a new non-coaxial turn, an inertial interaction will be generated which can be defined by a field of dynamic interaction, and with a magnitude defined by the Equation (6).
As a third corollary: A body with axial symmetry, equipped with intrinsic angular momentum on its main axis of inertia, cannot modify its state and become subject to another successive intrinsic rotation around another different axis as the result of vector addition of permanent rotations (L7-C3), which leads us to the fourth corollary stating that a free mass with intrinsic turn does not admit a vector composition of rotations, transforming the subsequent actions in movements of precession or orbital ones, with a centre external of the body in case an initial velocity  is present (L7-C4).
is present (L7-C4).
In the case of a body with angular momentum, submitted to an instant torque, an inertial reaction will be produced, which will modify the dynamic state of the body. Therefore we can state that: In the case of a body equipped with angular momentum, submitted to a noncoaxial instant torque, an inertial reaction will be produced that will modify the body’s path (L7-C5). This would be the case for a rotating body in a field of forces, when submitted to an instant torque as it will be able to modify its path, even contrary to the potential of the field, generating an apparently paradoxical movement.
And finally: The mobile’s path will be situated on the plane determined by the vector of the initial velocity  and an axis parallel to the momentum
and an axis parallel to the momentum  (L7-C6). This means that, if the variables are kept stable, the orbital movement will be flat.
(L7-C6). This means that, if the variables are kept stable, the orbital movement will be flat.
4.8. Eight Law
When to a body with axial symmetry, a rotation movement is applied around a main inertial axis, it will tend to maintain this rotation in a permanent way, even after the interruption of the forces which generated the rotation. If subsequently, it is submitted to a new non coaxial and constant momentum, it will be able to reach a permanent dynamic balance.
This Law can be called the Law of balance of Rotation movement. The dynamic analysis of rigid solid bodies equipped with intrinsic angular momentum, allows us to admit the possibility of reaching a dynamic balance. In case there is an absence of friction, the action of the noncoaxial constant external momentum will generate a perpetual dynamic balance.
In case the body initially has an intrinsic rotation and its centre of mass has a quantity of movement, with a linear velocity , given that the composition of movements will be produced between that one field and the field of the new angular displacement, the initial angular momentum being kept constant, we can deduce that: In nature, the rotational inertia is independent of the translational inertia (L8-C1).
, given that the composition of movements will be produced between that one field and the field of the new angular displacement, the initial angular momentum being kept constant, we can deduce that: In nature, the rotational inertia is independent of the translational inertia (L8-C1).
However, these inertial characteristics of mass allow comprehending the stabilising effect of rigid solid bodies with angular momentum where the rotational inertia allows them to have a dynamic stability.
We can also infer the existence of a correlation between the variation of the potential and kinetic energy. As a new corollary: In any phenomena of this nature in a gravitational and conservative field, we will see that that the difference of potential energy in two successive instants, will be able to transform into kinetic energy (L8-C2).
In phenomena of dynamic interactions raised in a gravitational field, a dynamic balance will be reached between the loss of potential energy and the increase of kinetic precession energy (L8-C3). As an example of this behaviour, rigid solid bodies submitted to intrinsic rotation with a point of support, which acquire an energetic balance, different for each level of energy due to their intrinsic angular momentum.
Another particular characteristic of this dynamic behaviour is the possible transference of kinetic energy of rotation into kinetic energy of translation, or, in general, the transference of energy. In these suppositions, a new corollary is complied with: To solid rigid bodies, equipped with intrinsic angular momentum, kinetic energy can be transferred, increasing its rotation velocity, its linear velocity or modifying its state of potential (L8-C4).
And lastly, generalising the deductions about the transference of energy, when analysing the structure of the rotational operator , the following corollary can be proposed: The transference of translational dynamic energy into rotational energy or vice versa, is possible (L8-C5).
, the following corollary can be proposed: The transference of translational dynamic energy into rotational energy or vice versa, is possible (L8-C5).
4.9. Ninth Law
The dynamic state of a body submitted to multiple momenta can be determined regarding to the contributing excitations and its precedence state in time.
The equations of the dynamic state of a body, will be in line with its starting dynamic state and the applied excitations, with the final dynamic state being able to vary according to the temporal succession of previous dynamic states or according to the precedence of the raised excitations which leads us to the following corollary: The commutative law is not applicable in case of rigid solid bodies with intrinsic angular momentum because the precedence in the action of momenta will determine different paths (L9-C1).
Also for rigid solid bodies equipped with angular momentum: The paths of the resultant movements will be different according to the temporal succession of the action of the excitations (L9-C2).
In these cases: the dynamic state of a body will be determined by logical sequences which can be represented by computer programmes (L9-C3). We cannot put forward in a single movement equation the different successsive dynamic states of a same body, submitted to various successive external actions, but we can use logical sequences which will allow us to design computer programmes.
And as a summary of all the above mentioned, we can put forward the following empiric law:
4.10. Tenth Law
From the observation of rigid solid bodies simultaneously equipped with rotation and orbit, the existence of inertial dynamic interactions can be inferred due to momenta of forces.
As a first corollary we can propose that: In phenomena of simultaneous rotation and precession, the existences of central force, does not have to be necessarily inferred, as there can exist another type of correlations in line with the real inertial and dynamic behaviour of rigid solid bodies (L10-C1).
Also this second corollary: There exists a physical correlation between the movements of rotation and of orbit which are shown simultaneously in nature, due to the inertial behaviour of rigid solid bodies. Both movements will be evident simultaneously, at least for those cases of rigid solid bodies with intrinsic angular momentum, submitted to non-coaxial constant torques (L10-C2).
And this third corollary, in absence of nutation, and as a logical result of the sixth corollary of the seventh Law: Rigid solid bodies equipped with intrinsic angular momentum and translation speed expose to constant momentum, will describe closed paths in a plane determined by the vector of initial velocity and that will possess an axis parallel to the acting momentum (L10-C3).
Therefore it can be inferred that the movements of rotation and orbit that are evident simultaneously in nature with closed paths and in a plane, can be due to dynamic interactions of inertial nature (L10-C4). This corollary allows us to define, in absence of nutation, the Precession Plane, determined by the sweep of the axis of the acting momentum, and that will contain the vector representing the translation velocity of the body.
We have proposed some laws of rotational dynamics of rigid solid bodies with axial symmetry or with revolution, when they are submitted to successive momenta of noncoaxial external forces, or even for those same bodies when equipped with intrinsic angular momentum. Therefore, these laws can be applied to different cases as for instance the boomerang or the spinning top.
In our opinion, the application of these laws of dynamic interactions to the phenomena that occur in nature with rigid solid bodies equipped with angular momentum, will allow an easier comprehension of these phenomena and the inference of new systems and artefacts that apply these laws. Simultaneously, it will allow a fuller comprehension of the physical laws of the universe in rotation, but in a constant dynamic balance, and bring these hypotheses even further to other areas of knowledge.
I have recently published a treatise of two volumes about the history of the human knowledge of the universe where these laws are included to better understand our cosmological environment [18]. Moreover, a video has been created to present the treatise [19].
5. Other Laws
The laws put forward, are referring to the exposed dynamic hypotheses, starting from the stated axioms. They are, therefore, the laws that correspond to a specific dynamic state and specific external excitations. In the case of other idealised models or other different hypotheses, other differentiated behaviour laws could be given as a result, starting from the mentioned axioms.
For example, in the case of instant turns that could generate momenta of interactions instant as well, or in the case of translation speeds variable in time. In these new suppositions, new equations of movement would be deduced as well as new behaviour laws. In every case, the new movement equations would allow to make dynamic behaviour deterministic whereas up to now they were understood as undetermined or chaotic.
Also to be noted is that the laws have been developed for a simple and very specific case, which is for rigid solid bodies with axial symmetry where the fields of velocities generated by non-coaxial external successive actions are easily to determine. The geometry itself of bodies could also have a bearing on its final dynamic behaviour.
Therefore, the stated laws are referring to a simplified supposition determined by the exposed idealised model. This model is based on a stable dynamic situation and a defined inertial reaction, hypothesis which avoids, for instance, transitorily dynamic regimes. It is evident that the inertial reaction is not instant, so that there will also be present an initial transitory regime, or even in any time where the environmental conditions are modified. In this case, we are of the opinion that more complex temporal dynamic reactions will be generated, such as, for instance, the movements of nutation.
6. Conclusions
With this analysis, we believe to be given a full answer to our initial aporia between constant turn and orbital movement, therefore justifying the coincidence in nature where mobiles are rotating and orbiting simultaneously, based on the peculiar inertial behaviour of mass.
Throughout our exposition, we have tried to avoid the concept of inertial force and we have substituted it by inertial reactions. No existence of real forces can be inferred from the observation of matter. Although we can infer the existence of the non-homogeneous distributions of velocities, whose derivative generates an inertial field of accelerations, which neither are homogeneous, it can be interpreted as a field of inertial forces.
It is necessary to underline that this field of inertial forces is not the result of a transformation of reference axes, as is the case for other dynamic suppositions. But it is generated in the rigid body as an inertial reaction that is submitted to the excitation.
We would like to note that in our deductive reasoning, we have introduced a discriminating hypothesis, in the case of the body’s translation movement, when we propose that the field of translation speeds will be coupled to the anisotropic field of inertial speeds created by the second non-coaxial torque. Finally, an orbital motion is generated, simultaneous with the initial intrinsic rotation of the mobile. This new orbital movement generated by a non-coaxial momentum will be defined by the rotation of the velocity vector of translation, the latter kept constant in module.
In previous texts, we have proposed that, through this analysis, the nature of any movement in space can be determined and predicted, defining its relativity [6 IX]. The movement equation that is proposed, and the laws that are formulated, permit the initiation of the structuring of a rational mechanics and of a rotational dynamics based on principles and axioms, for bodies submitted to accelerations by rotations, clearly differentiated from classical mechanics.
In this new rational structure, phenomena that are paradoxical or alien to the main structure should not be present, as happens in classical mechanics, with the so called gyroscopic torque or fictitious forces.
The Theory of Dynamic Interactions is a logical-deductive system constituted from some dynamic hypotheses. By means of the observation of nature, the establishing of some initial hypotheses, and starting from axioms and postulates, we have constructed a structure of knowledge in relation to rigid solid bodies, when submitted to successive accelerations by rotation. The physical-mathematical model obtained allows us to interpret the observable behaviour of these bodies, subject to successive non coaxial torques, according to deduced laws, as well as to extract new consequences, inferences and predictions. The theory has been checked and confirmed by experimental tests.
This text does not pretend to challenge the laws of Newton; what has been developed is a conceptual structure complementary to classical mechanics, for systems accelerated by rotations. We propose a theory based on a specific rotational algebra for non-inertial environments where the starting hypotheses that the laws of translational classical mechanics are based on, are not respected. We propose the exploration of a new niche of knowledge for some very specific, but not trivial dynamic conditions that are repeated in our universe.
Also it is noteworthy that, through the development of these studies, full coherence has been obtained between the hypotheses of the beginning, the applied principles and axioms, the developed physical-mathematical model, the obtained movement equation, the deduced laws, the reached simulation models and the conducted experimental tests [20]. We have also referred to examples in nature which support the Theory of Dynamic Interactions, all endorsing the laws proposed in this text.