A Modified Formal Theory on Semi-Relativistic Effects during Electron Emission from Metallic Surfaces upon the Impact of High Energy Particles ()
1. Introduction
In the last three decades significant progress has been made in understanding the atomic physics of electronatom ionization both theoretically and experimentally for relativistic energies [1-14] as well as for non-relativistic energies [15-26]. Capabilities of different theoretical models in reproducing various features of experimental results have been widely tested for different kinematical conditions. Study of energy spectrum of ejected electrons could be very interesting. The complexity of this reaction is already revealed in the simplest case of low-energy electron impact ionization of atomic hydrogen where final state interactions of escaping particles strongly modify the observed electron spectra [16,21]. Hence a realistic approximate eigenfunction of the non-separable three body Hamiltonian is essential. Generally, a theoretical description of this process from solid targets has to deal with various aspects of the beam-solids interactions. A relativistic charge particle impinging on a metallic target, which is the study of this work, leads to charge-density fluctuation of the solid. Asymptotically, this causes an image-charge distribution of the incoming and outgoing particles [22]. Moreover, the motion of the various electrons is periodically distributed by the interaction with the bulk potential [24,25]. The aim of this paper is to investigate the energy spectrum of electron ejection from clean metalic surfaces upon higher charged particle impact for relativistic energies [10,12,23]. The present study of the formal theory is the assumption that the degrees of freedom of the projectile can be decoupled from those of the target. This is justified, since we assumed the momenta of the incoming and outgoing electron to be considerably larger than the Fermi momentum. To obtain the analytical theory that can be analyzed, a Jellium wave function [23] with suitable spinors [12] of the initially bound electron is assumed. Asymptotic image-charge distribution of the Vacuum electron is taken into account. As well as the binary collision of the projectile with the bound electron, the scattering of the incident particle from the multicenter bulk potential is treated in the kinematic approximation [25,26]. A screened Coulomb muffin-tin bulk potential is adopted. Recently using the multiple scattering theory [17] multiplied with some spinors has calculated the energy spectrum of scattered electrons in k-shell ionization of medium heavy atoms by relativistic electrons [10-12] which agree nicely with experiments. In the present study we developed the theory of relativistic 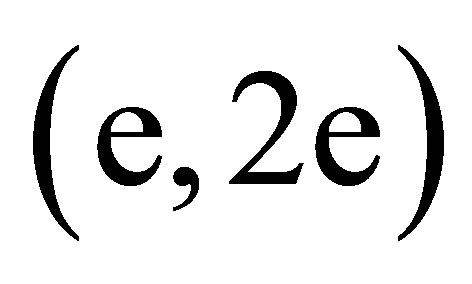 scattering mechanism process using a Jellium wave function [23] of the undistributed surface in the initial state. In addition, image-charge final state electron surface interactions have been included. Moreover, the scattering of the projectile from the multicentre bulk potential is considered. The proposed theory will provide scattering cross-sections results of different kinematical conditions. Hence we introduced a modified theory on semi-relativistic effects during electron emission from aluminium surfaces upon the impact of high energy particles.
scattering mechanism process using a Jellium wave function [23] of the undistributed surface in the initial state. In addition, image-charge final state electron surface interactions have been included. Moreover, the scattering of the projectile from the multicentre bulk potential is considered. The proposed theory will provide scattering cross-sections results of different kinematical conditions. Hence we introduced a modified theory on semi-relativistic effects during electron emission from aluminium surfaces upon the impact of high energy particles.
2. Theory
In this theory, we consider an atomic scattering system consisting of a projectile with nuclear change 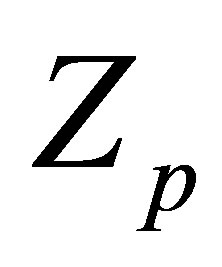 and mass
and mass 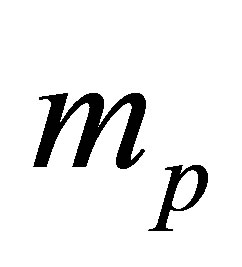 being inelastically scattered from a clean metallic semi-infinite solid ejecting one electron into the vacuum level of the solid. Then the total Hamiltonian of the projectile-solid system is
being inelastically scattered from a clean metallic semi-infinite solid ejecting one electron into the vacuum level of the solid. Then the total Hamiltonian of the projectile-solid system is
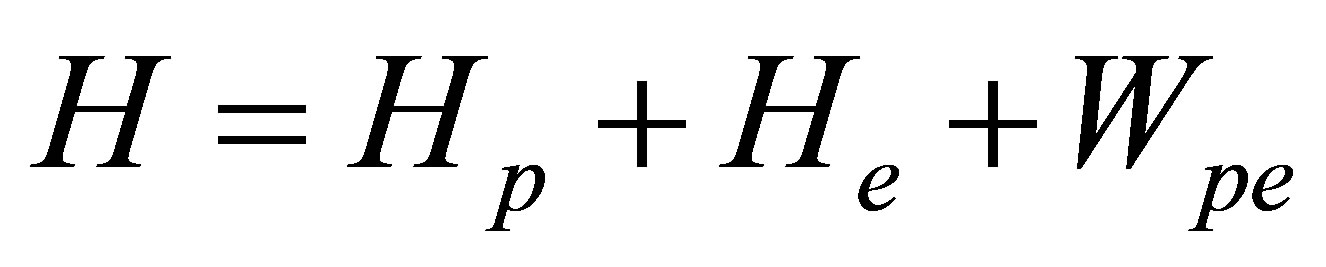 (1)
(1)
where 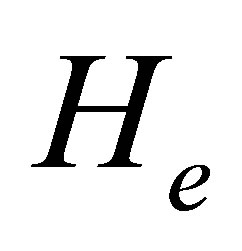 is the Hamiltonian of the simi-infinite solid in the absence of the projectile, Wpe is the projectileejected electron interaction, and Hp represents the projectile-crystal interaction and contains the plasmon and phonon modes and their interaction with electron. The initial and final state boundary conditions are specified by eigenstates
is the Hamiltonian of the simi-infinite solid in the absence of the projectile, Wpe is the projectileejected electron interaction, and Hp represents the projectile-crystal interaction and contains the plasmon and phonon modes and their interaction with electron. The initial and final state boundary conditions are specified by eigenstates 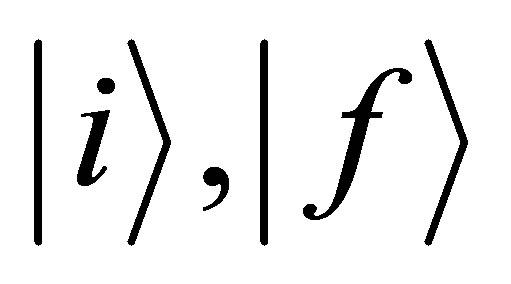 of asymptotically unperturbed initial and final channel Hamiltonian
of asymptotically unperturbed initial and final channel Hamiltonian 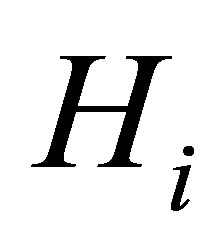 and
and 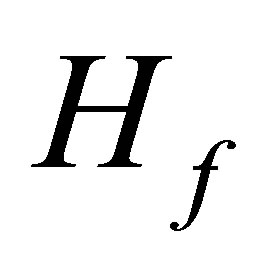 respectively, i.e.,
respectively, i.e.,
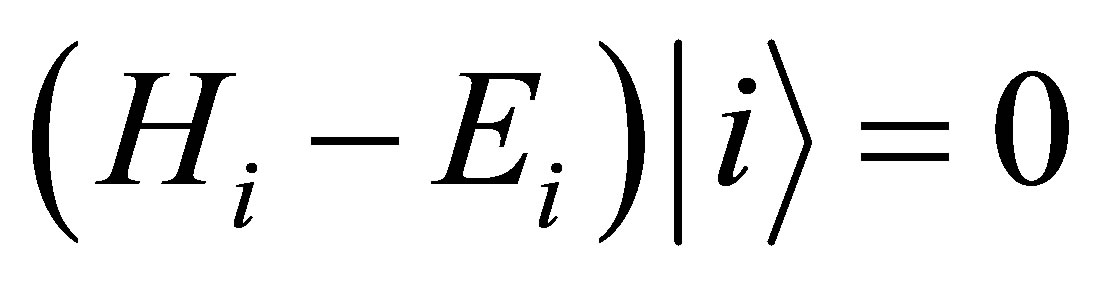 (2)
(2)
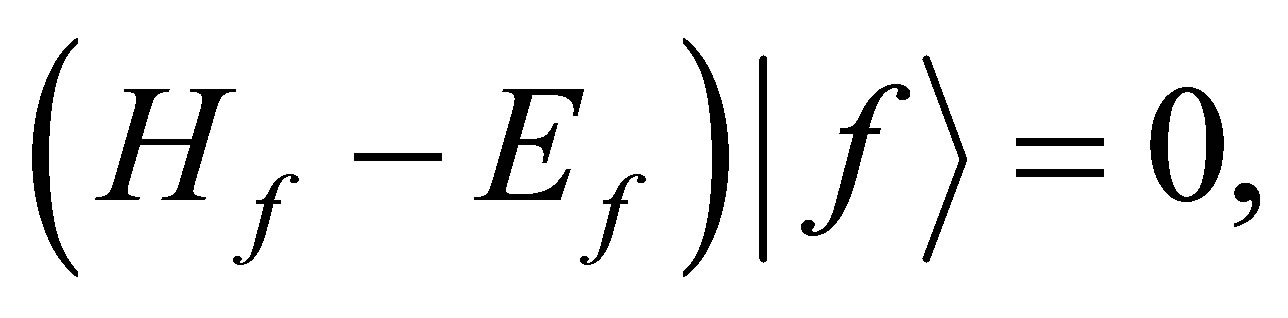 (3)
(3)
where 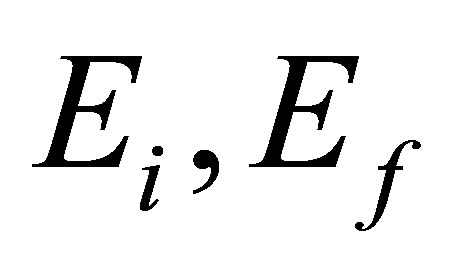 are the corresponding asymptotic eigen energies. The transition amplitude T for the scattering system from initial state
are the corresponding asymptotic eigen energies. The transition amplitude T for the scattering system from initial state , to the final state
, to the final state 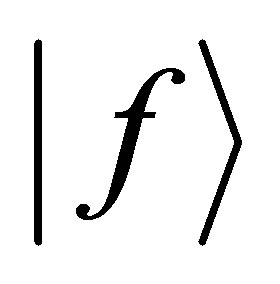 is determined by the prior form
is determined by the prior form
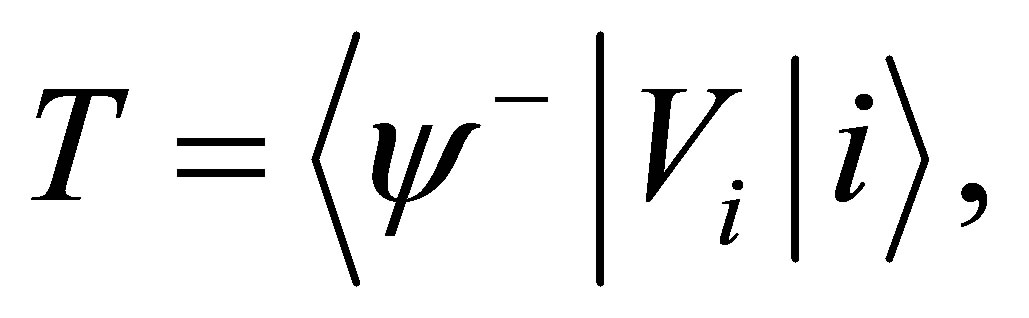 (4)
(4)
or the post form
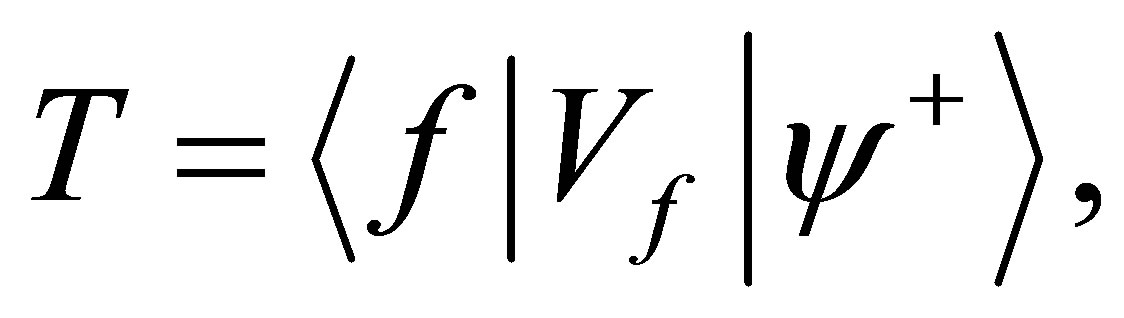 (5)
(5)
where 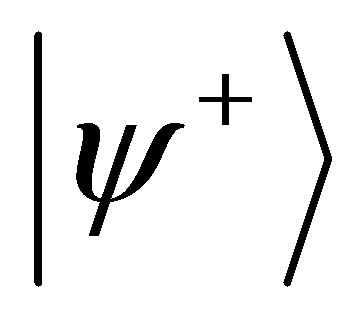 and
and 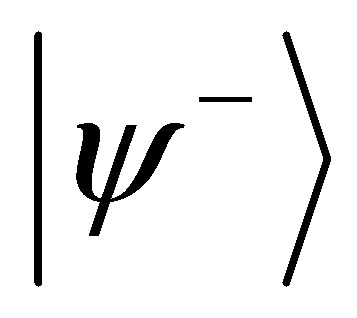 are the eigensates of the total Hamiltonian H according to the state
are the eigensates of the total Hamiltonian H according to the state  and
and 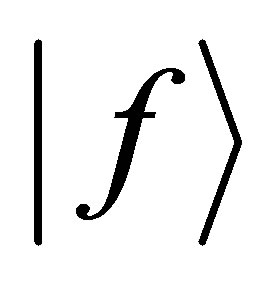 respectively. From Equations (4) and (5) the perturbations potential
respectively. From Equations (4) and (5) the perturbations potential 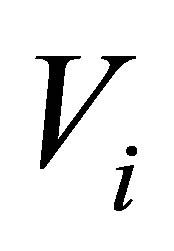 and
and 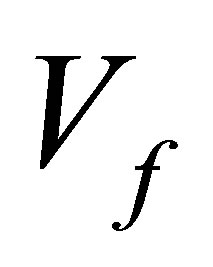 are given by
are given by
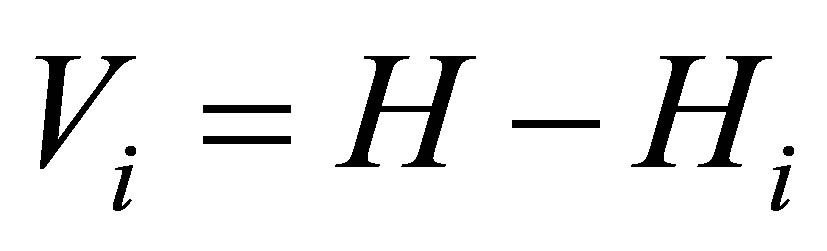 (6)
(6)
 . (7)
. (7)
The eigenstates 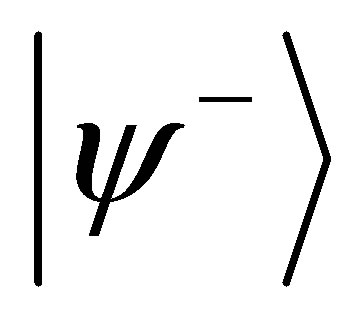 of H can be written as
of H can be written as
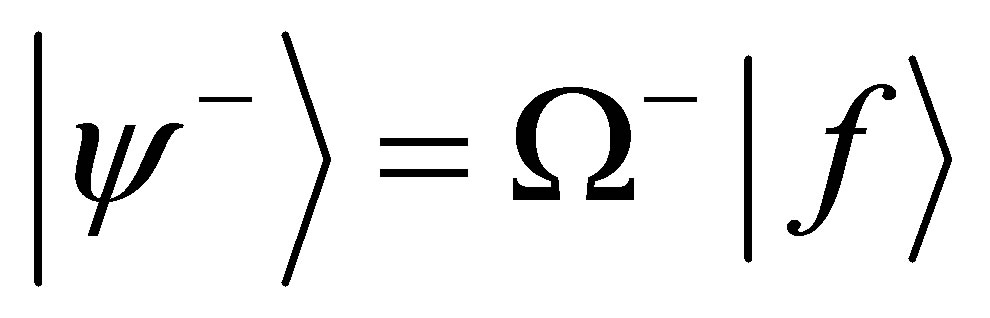 (8)
(8)
where the MØller wave operator 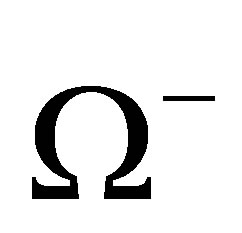 is given by
is given by
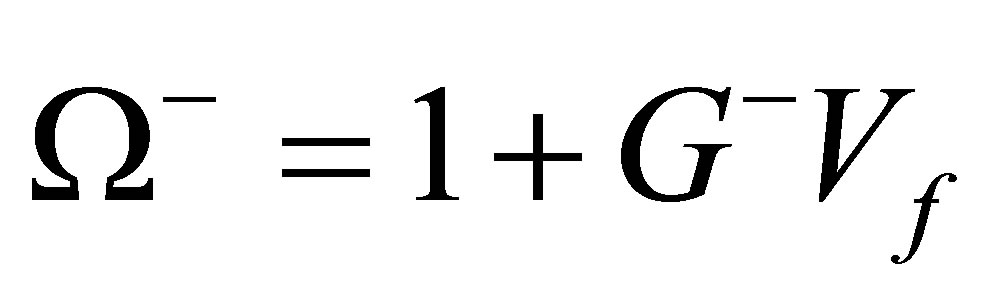 (9)
(9)
where 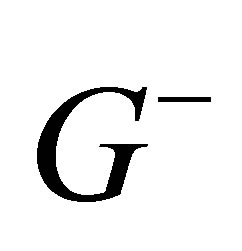 is the Green operator of the total Hamiltonian H. Combining Equations (9), (8) and (4), the T matrix element may be written as
is the Green operator of the total Hamiltonian H. Combining Equations (9), (8) and (4), the T matrix element may be written as
 (10)
(10)
where
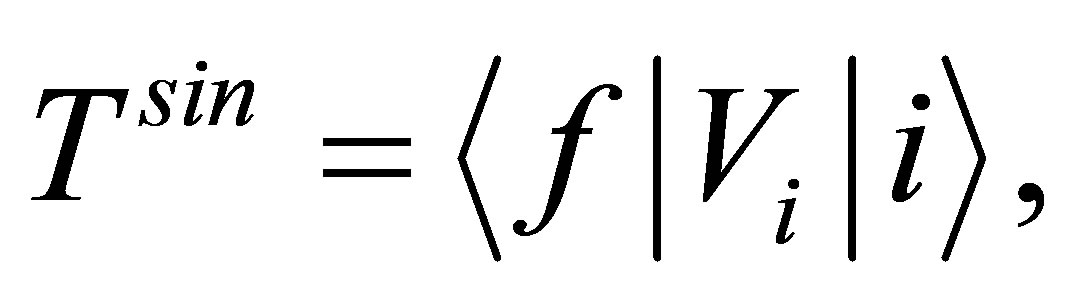 (11)
(11)
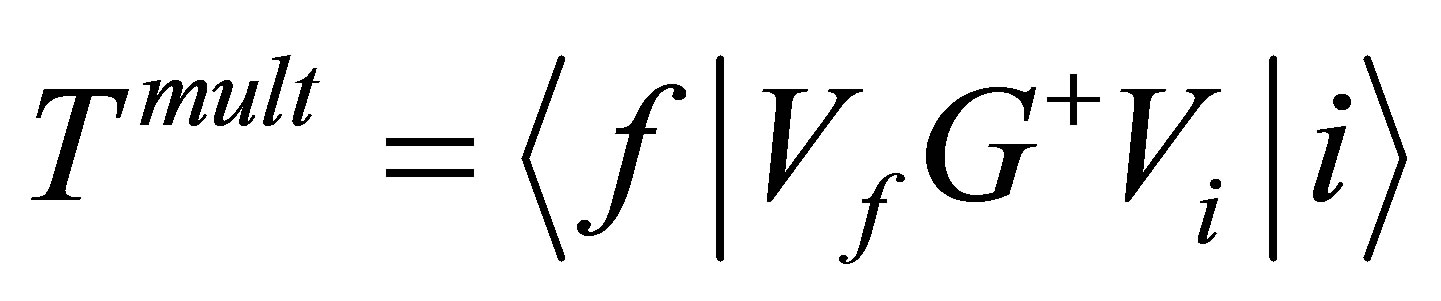 . (12)
. (12)
Here assuming 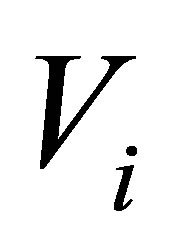 to be a multiple-center potential, the first term of Equation (10), that is
to be a multiple-center potential, the first term of Equation (10), that is 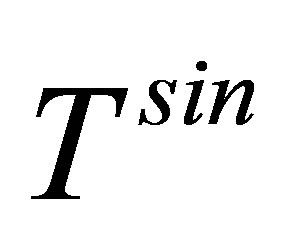 describes the transition of the system from state
describes the transition of the system from state  to
to 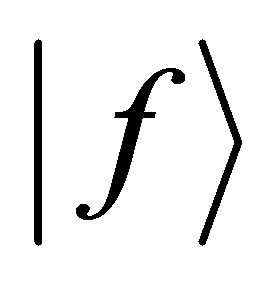 due to a single scattering from each individual scattering center. One center and multicenter multiple scattering is contained in the matrix element
due to a single scattering from each individual scattering center. One center and multicenter multiple scattering is contained in the matrix element 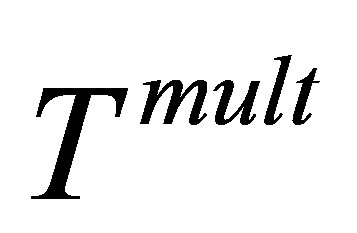 in Equations (10) and (12), since the Lippmann-Schwinger equation of the total Green operator leads to the expansion
in Equations (10) and (12), since the Lippmann-Schwinger equation of the total Green operator leads to the expansion
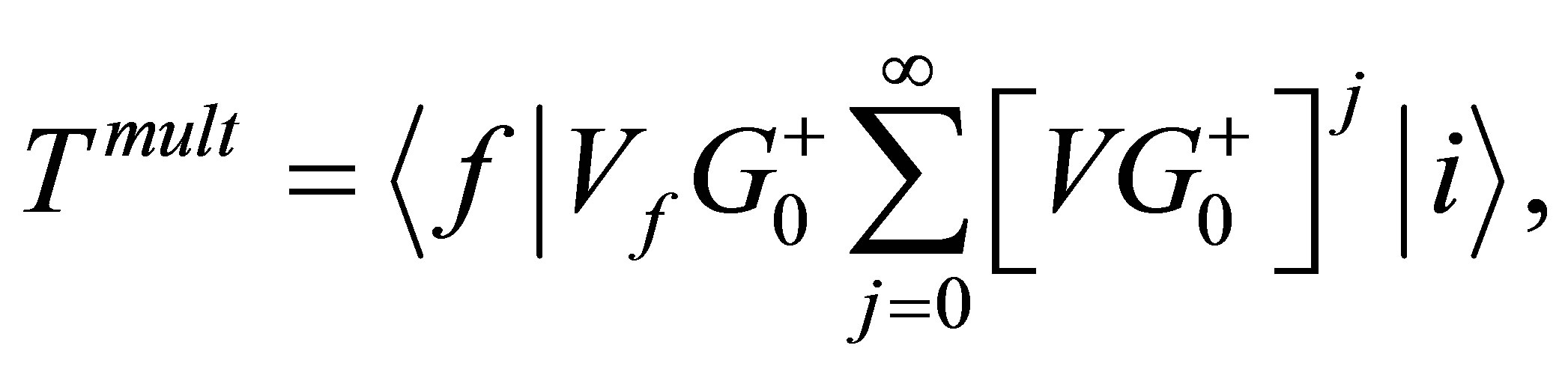 (13)
(13)
where 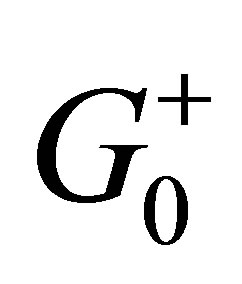 and V are the full free propagator and the total potential of the projectile-solid compound. It should be noted here that the labels
and V are the full free propagator and the total potential of the projectile-solid compound. It should be noted here that the labels 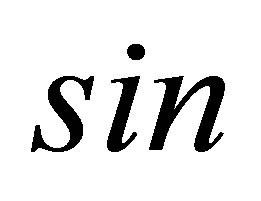 and
and 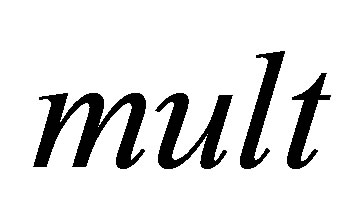 of the amplitudes
of the amplitudes 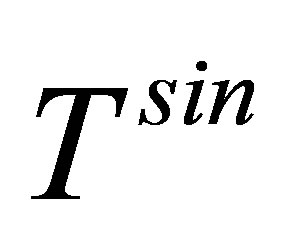 and
and 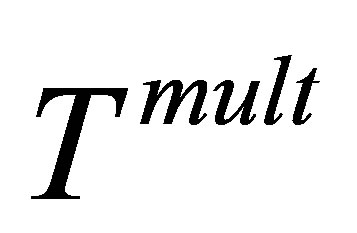 refer to single and multiple scattering specifically from the potential
refer to single and multiple scattering specifically from the potential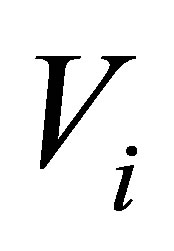 . The potential
. The potential 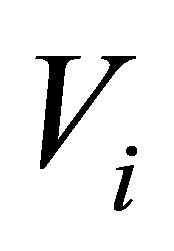 in the initial channel can be written as
in the initial channel can be written as
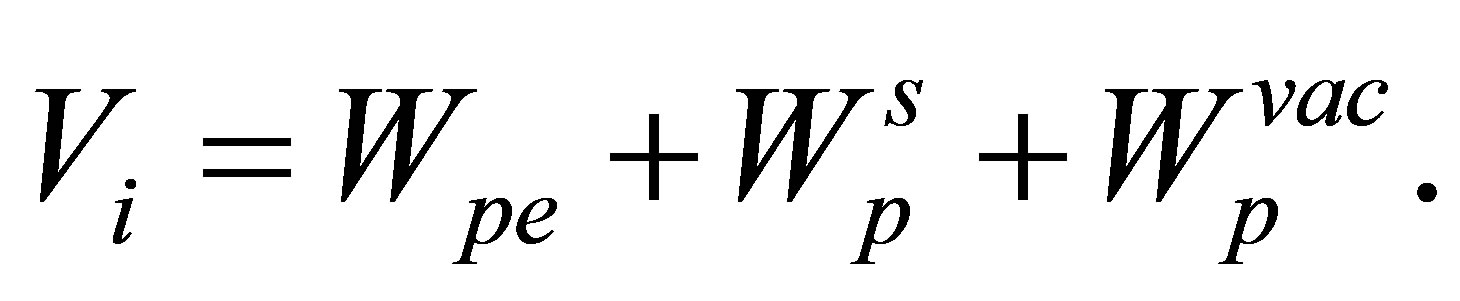 (14)
(14)
The operator 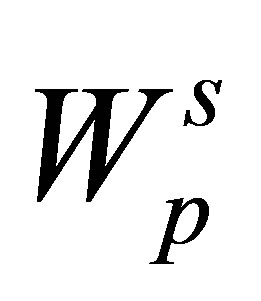 stands for the particle-bulk interaction and its explicit functional form is specified below. The potential
stands for the particle-bulk interaction and its explicit functional form is specified below. The potential 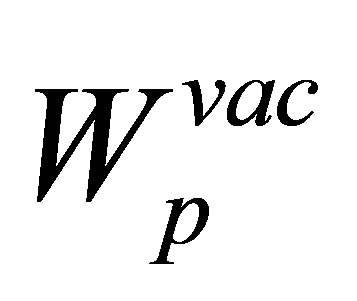 is less prominent. Since it is an asymptotic (imagine charge) perturbation. For the asymptotic final-channel Hamiltonian [23] is given by
is less prominent. Since it is an asymptotic (imagine charge) perturbation. For the asymptotic final-channel Hamiltonian [23] is given by
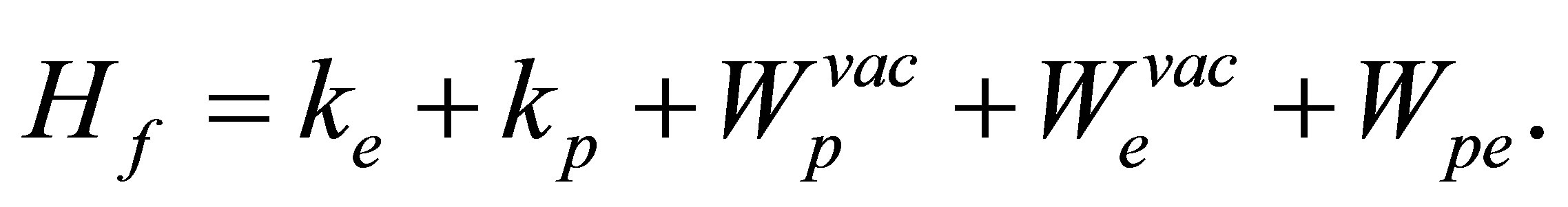 (15)
(15)
Here the kinetic-energy operator of the secondary electron is referred to by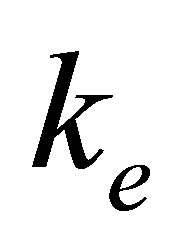 , whereas
, whereas 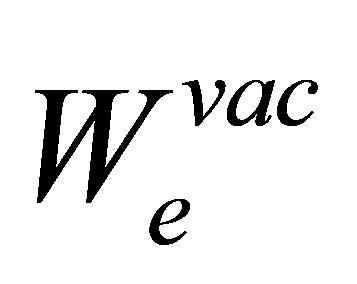 amounts to the asymptotic final state interaction of this electron with semi-infinite solid. The choice Equation (15) leads to the final-channel distribution operator
amounts to the asymptotic final state interaction of this electron with semi-infinite solid. The choice Equation (15) leads to the final-channel distribution operator
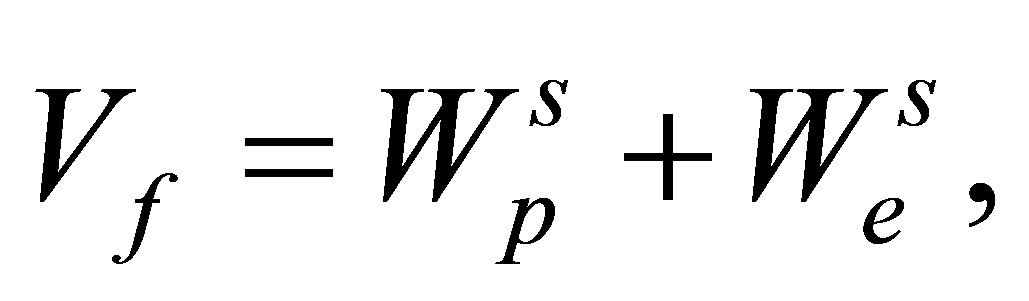 (16)
(16)
where 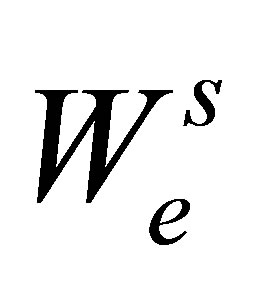 denotes the short-range interaction of the secondary electron with the surface. Upon substitution of Equation (14) into Equation (11), the matrix element
denotes the short-range interaction of the secondary electron with the surface. Upon substitution of Equation (14) into Equation (11), the matrix element 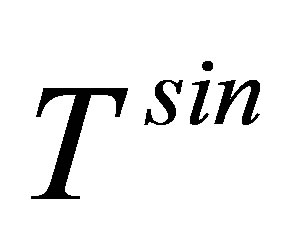 can be decomposed into the form
can be decomposed into the form
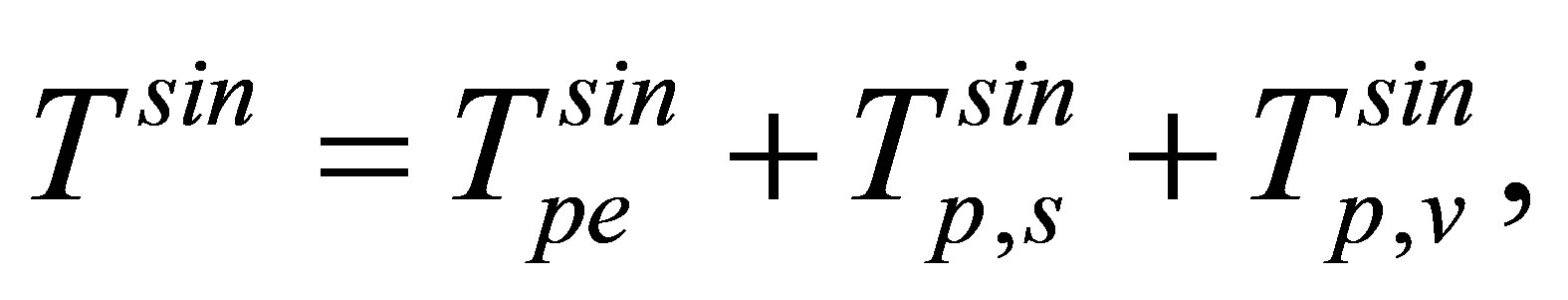 (17)
(17)
where
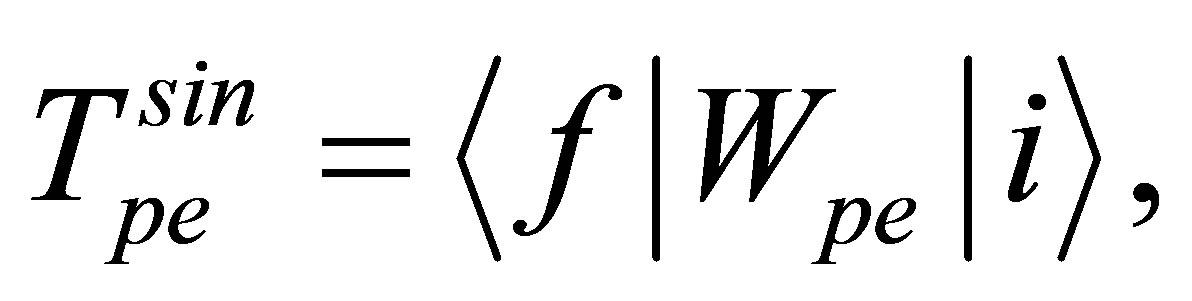 (18)
(18)
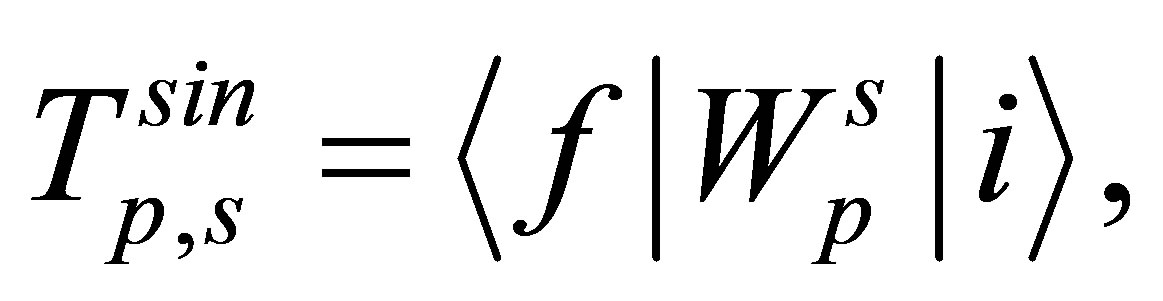 (19)
(19)
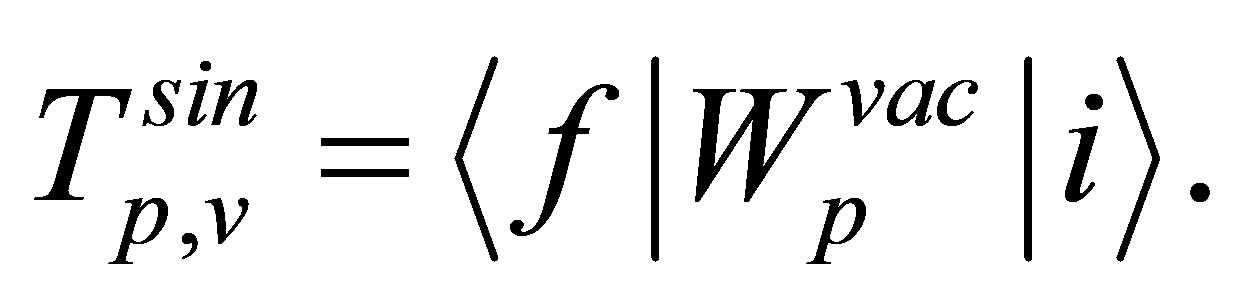 (20)
(20)
The amplitudes, given by Equations (18) and (19), provide the first-order approximation of the matrix element T. The term in Equation (20) is less prominent since 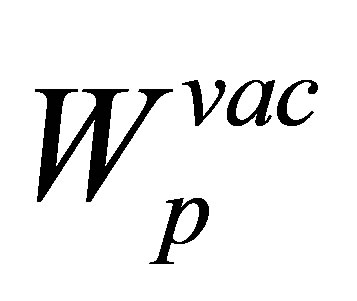 is an asymptotic (image charge) perturbation. Hence it has no significant contribution to the
is an asymptotic (image charge) perturbation. Hence it has no significant contribution to the 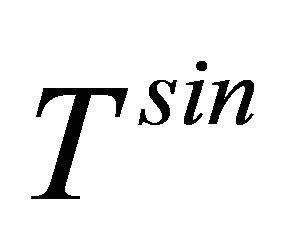 term. So, the amplitude, given by Equation (20) is neglected here.
term. So, the amplitude, given by Equation (20) is neglected here.
2.1. Analytical Calculation of the Transition Amplitude Term 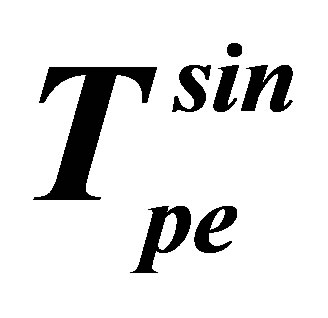 in Relativistic Effects
in Relativistic Effects
In a position-space representation the transition operator occurring in the Equation (18) has the form
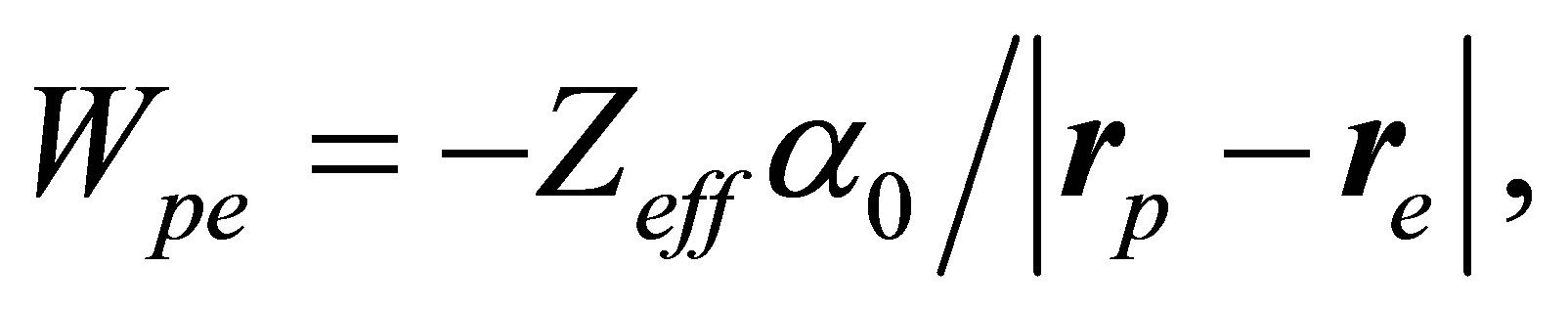 (21)
(21)
where 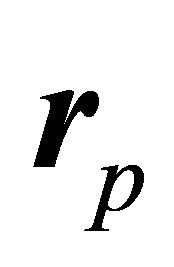 and
and 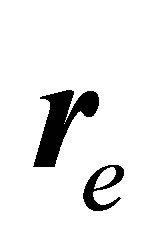 are the position vectors of the projectile and ionized electron respectively. Also
are the position vectors of the projectile and ionized electron respectively. Also 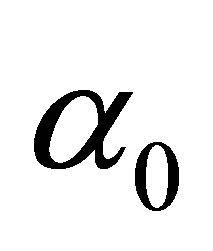 is time structure constant and
is time structure constant and 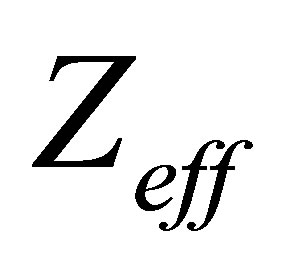 (effective nuclear charge) = Nuclearcharge
(effective nuclear charge) = Nuclearcharge 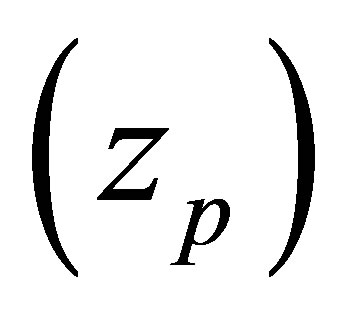 − 0.3. To avoid difficulties arising from the infinite range of coulomb interactions we introduce the cutoff potential [23]
− 0.3. To avoid difficulties arising from the infinite range of coulomb interactions we introduce the cutoff potential [23]
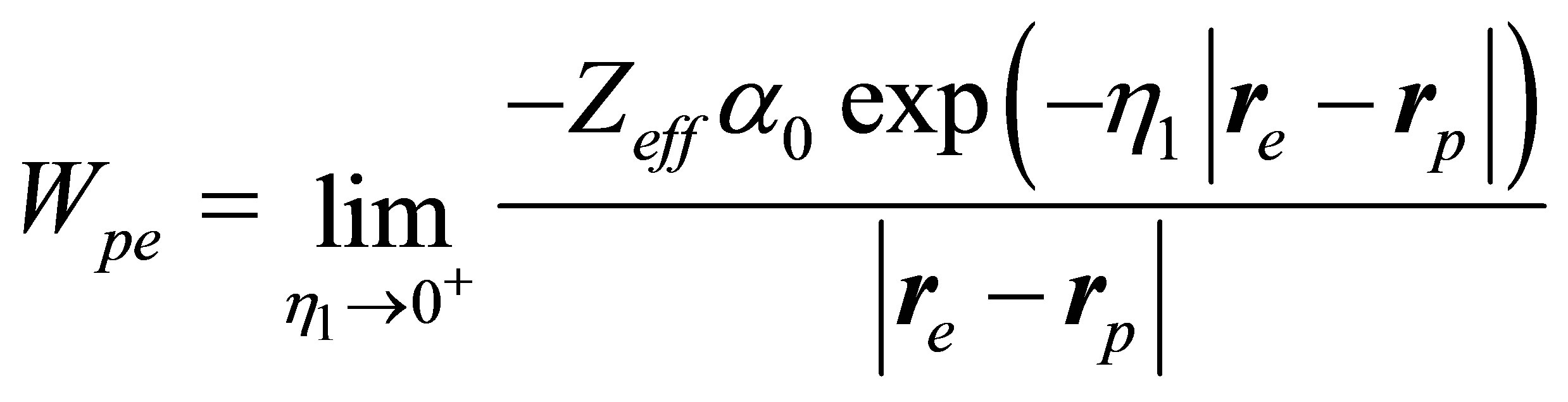 . (22)
. (22)
The eigenfunction of 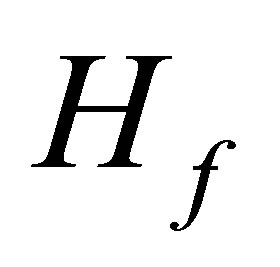 of Equation (15) at a given asymptotic energy
of Equation (15) at a given asymptotic energy 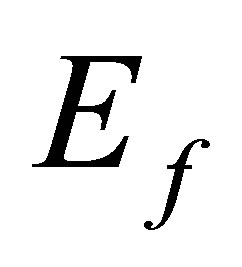 [23] is readily deduced in semirelativistic form [1,12] as
[23] is readily deduced in semirelativistic form [1,12] as
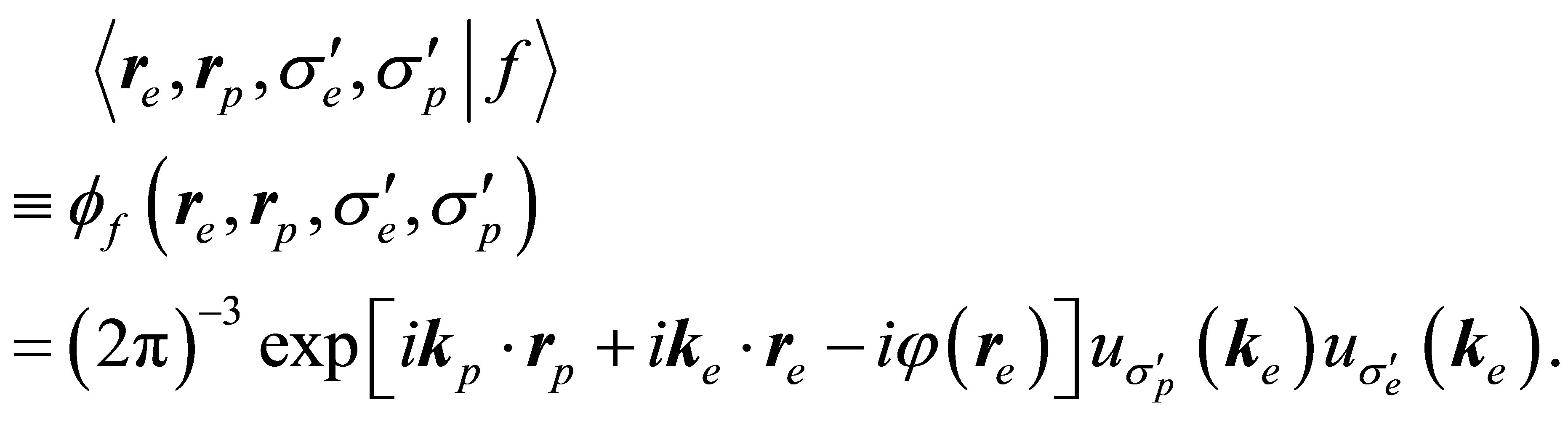 (23)
(23)
In addition the Jelliun wave function [23] can be expressed in terms of reflection and transmission coefficient may be written as in semi-relativistic form [1,12] as
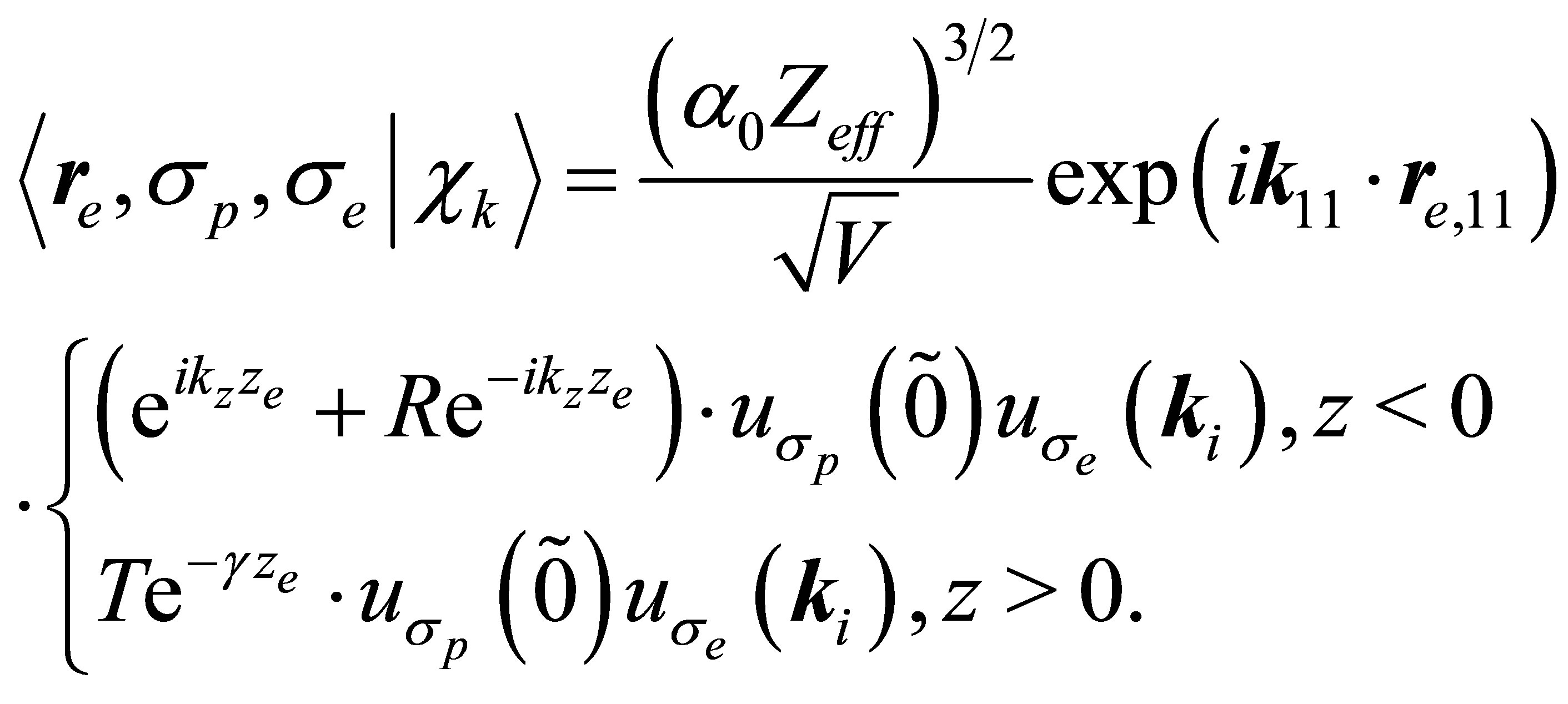 (24)
(24)
Here 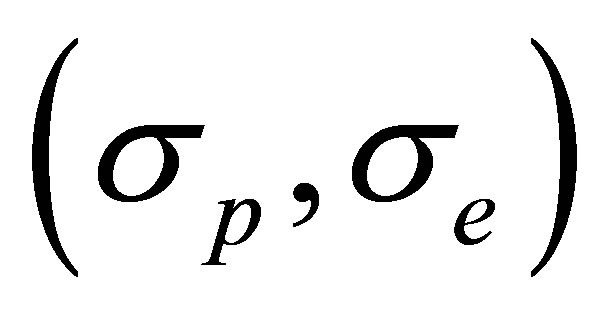 and
and 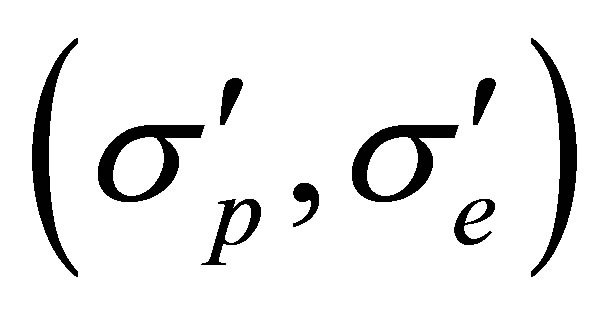 are the spin co-ordinates in the initial and the final states of the electrons.
are the spin co-ordinates in the initial and the final states of the electrons. 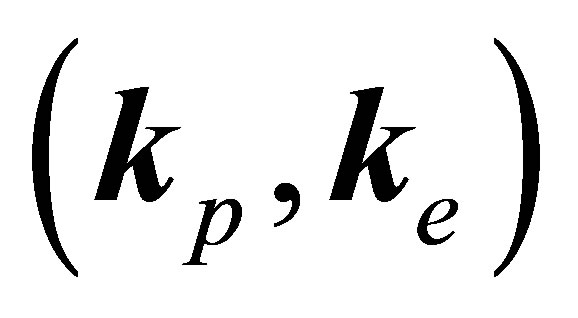 and
and 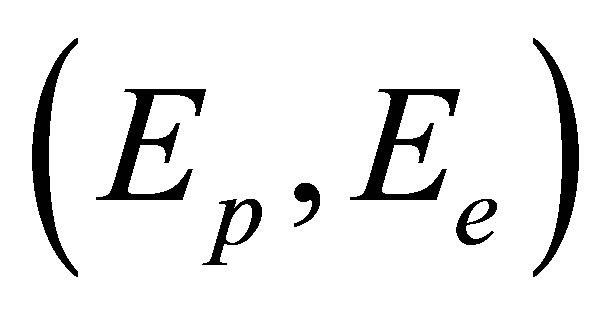 are the momenta and energies of the final two electrons and
are the momenta and energies of the final two electrons and 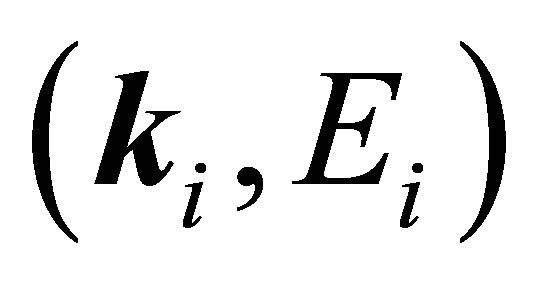 are the momentum and energy of the incident electron. Here
are the momentum and energy of the incident electron. Here  and
and 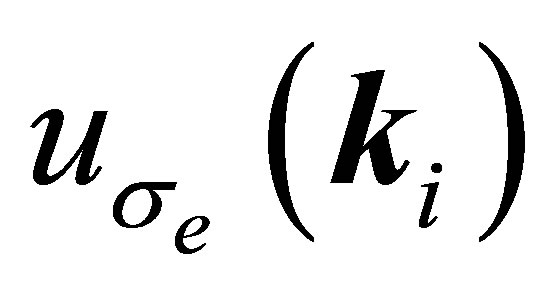 are the Dirac spinors of the atomic electrons and the incident electron. Also
are the Dirac spinors of the atomic electrons and the incident electron. Also 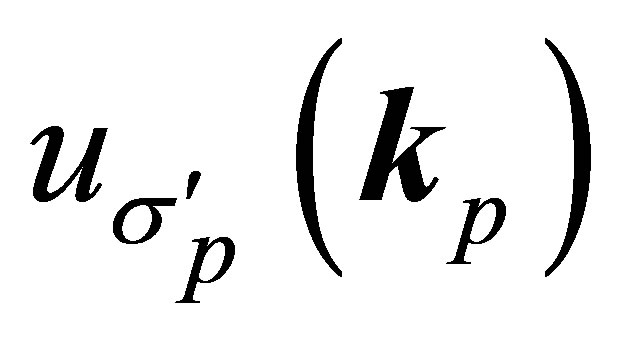 and
and 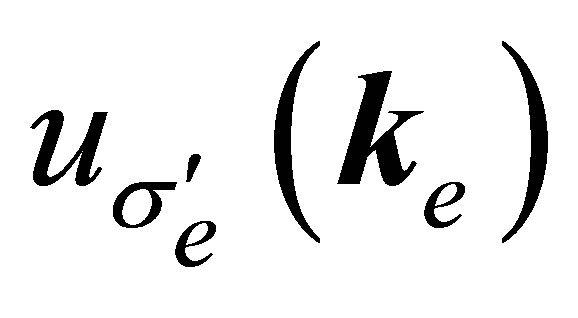 represent the Dirac spinors of scattered and ejected electron. In the Equation (23) the term
represent the Dirac spinors of scattered and ejected electron. In the Equation (23) the term 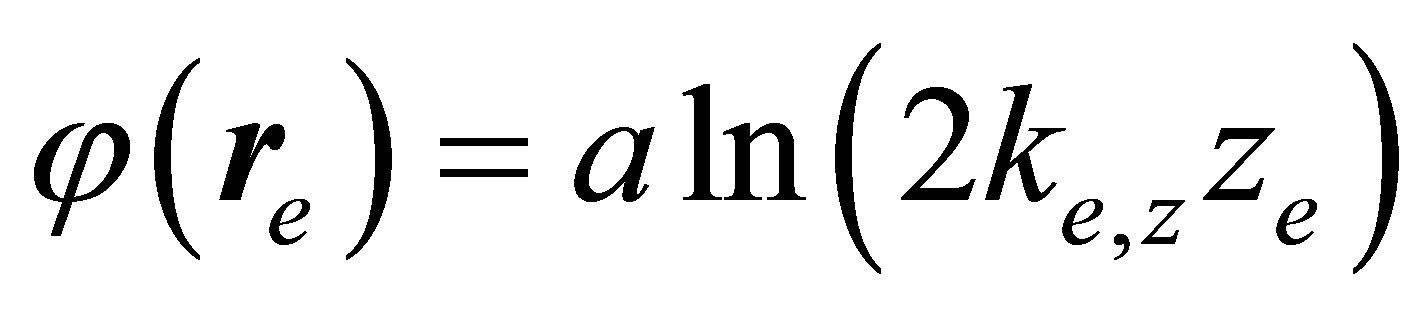 is the phase modification of the asymptotically free electron motion due to its image charge where
is the phase modification of the asymptotically free electron motion due to its image charge where 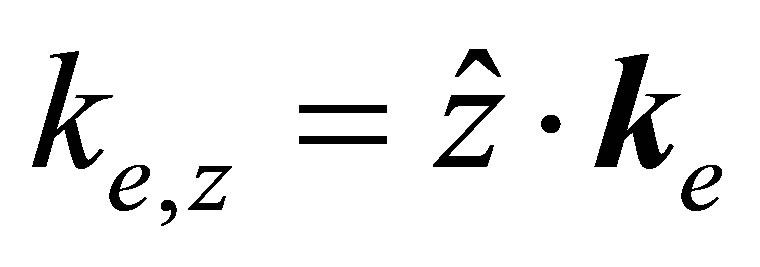 and the Sommerfeld parameter
and the Sommerfeld parameter 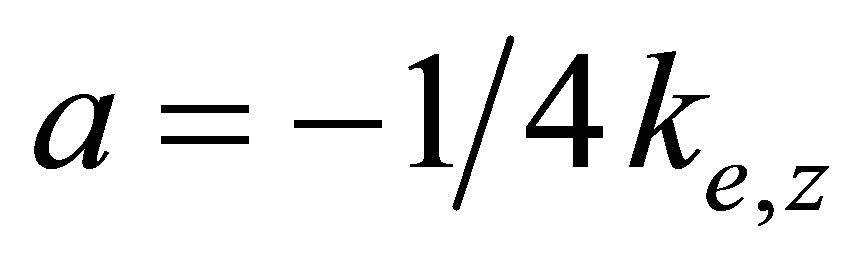 indicates the strength of this interaction. In case
indicates the strength of this interaction. In case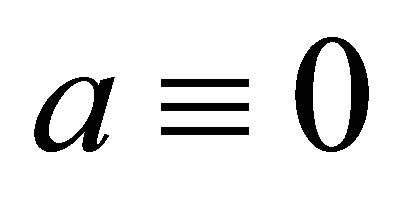 , we end up with the final state being a product of the two free-particles states. The final state energy is given by
, we end up with the final state being a product of the two free-particles states. The final state energy is given by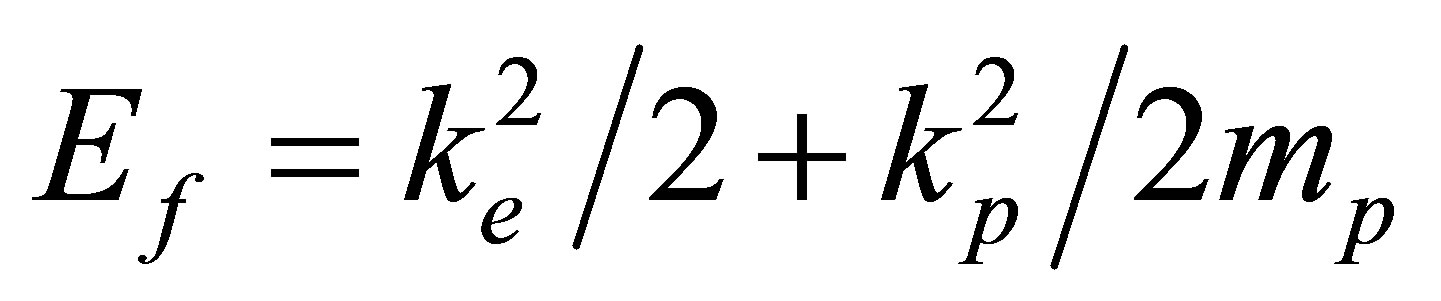 . The refection and transmission coefficient R and T are given by
. The refection and transmission coefficient R and T are given by
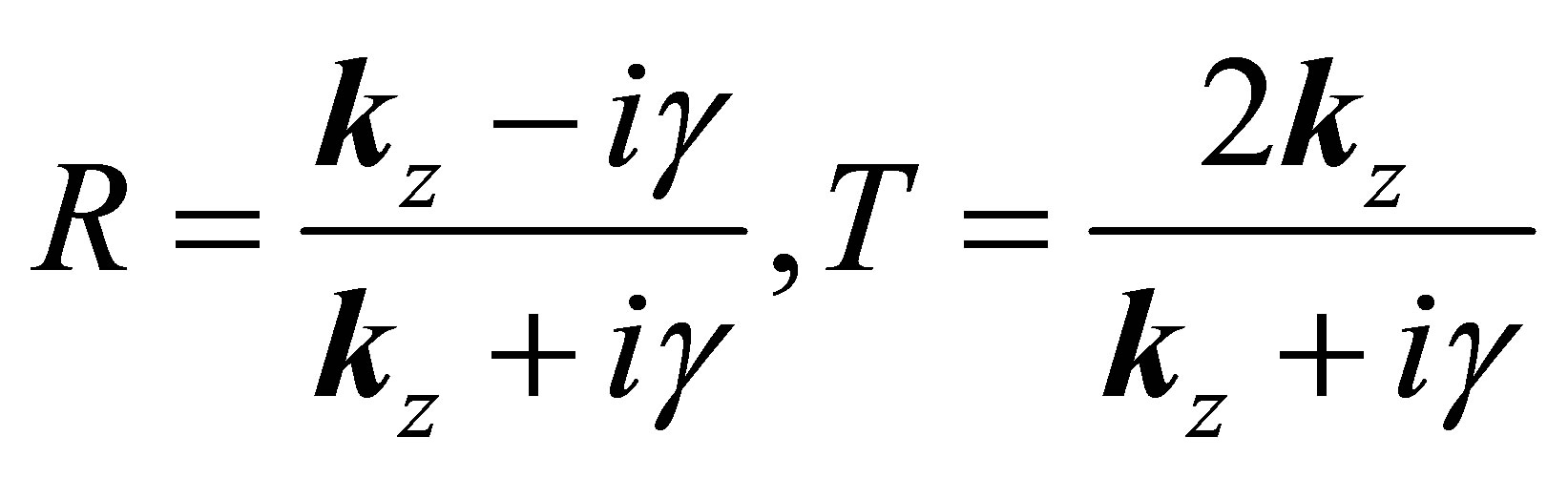 (25)
(25)
and
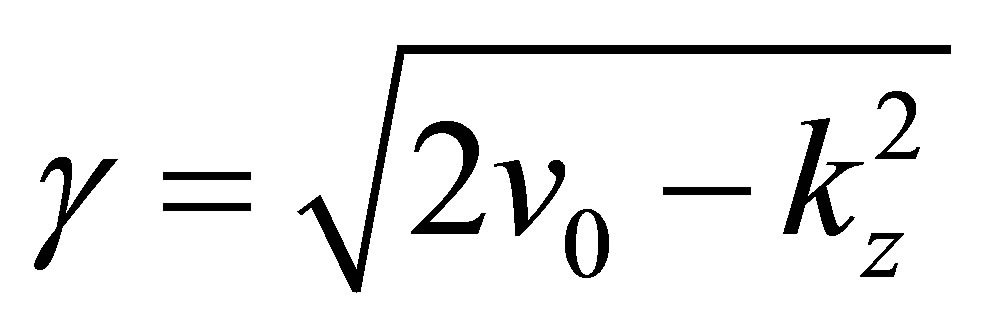 . (26)
. (26)
In the present case, the transition amplitude term 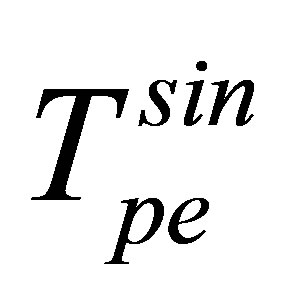 may be written as in semi-relativistic integral form [23] as
may be written as in semi-relativistic integral form [23] as
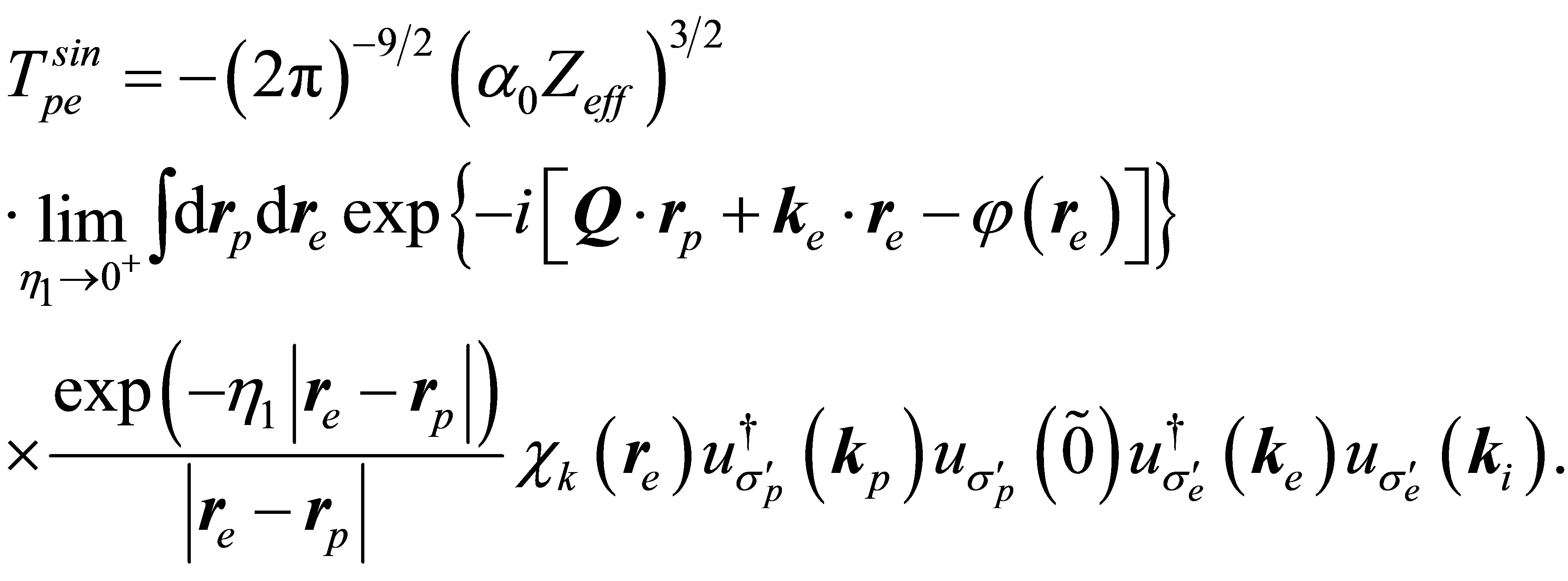 (27)
(27)
Therefore
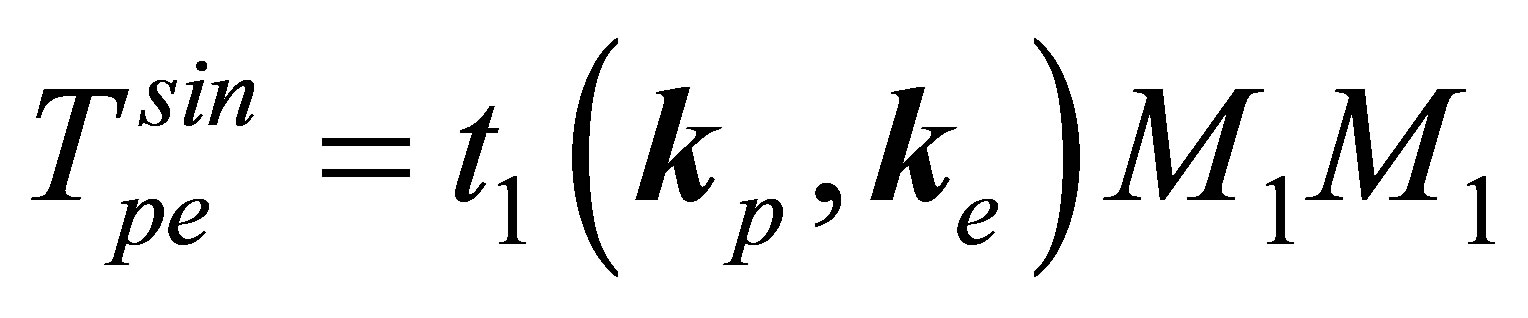 (28)
(28)
where
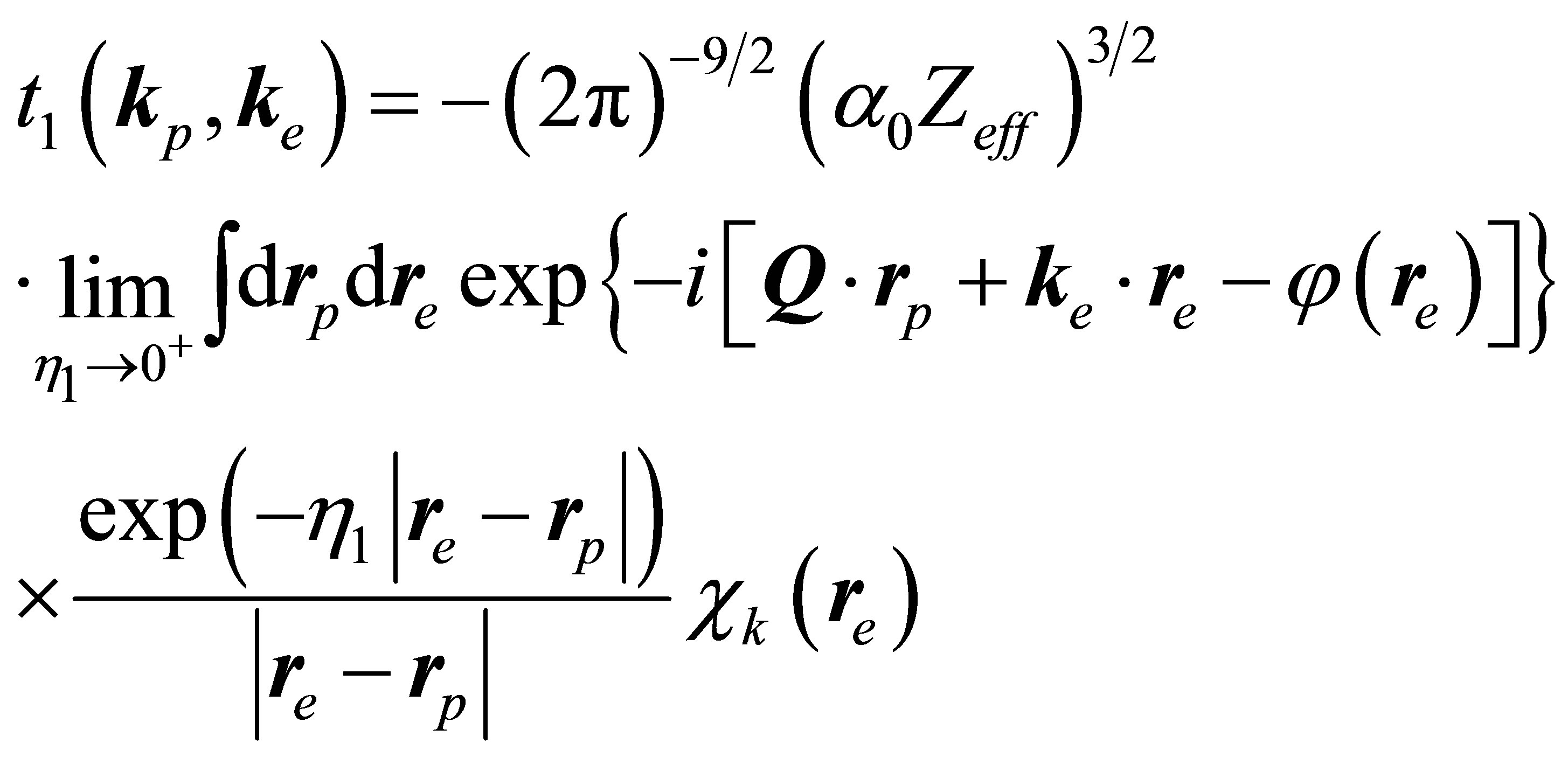 (29)
(29)
and
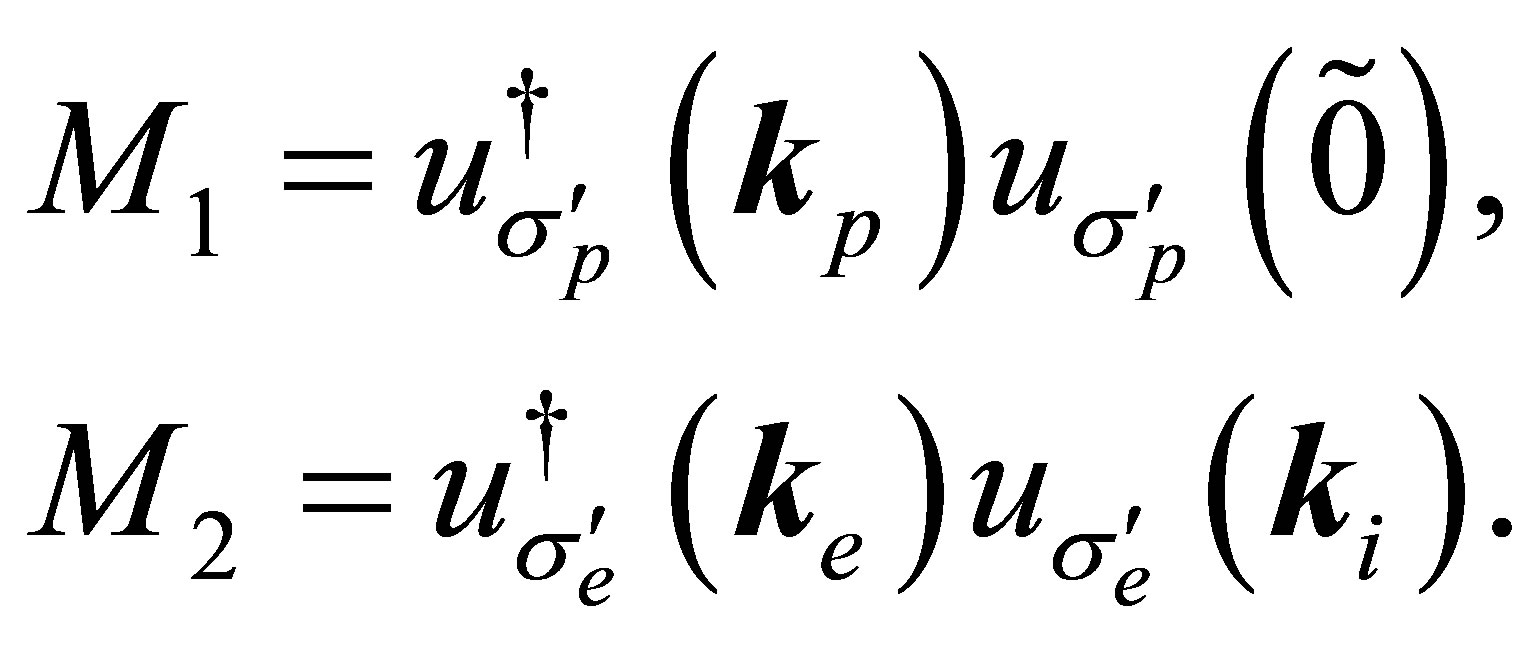 (30)
(30)
Upon replacing the logarithmic phase in Equation (29) by its integral representation, given by
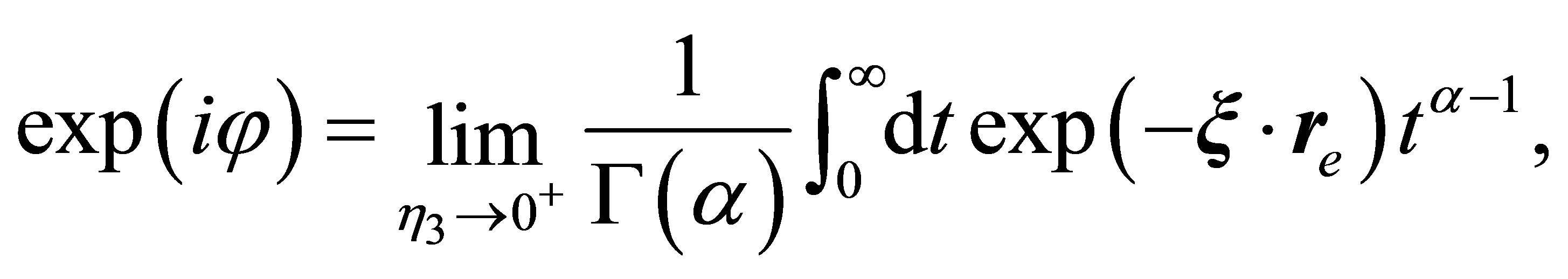 (31)
(31)
where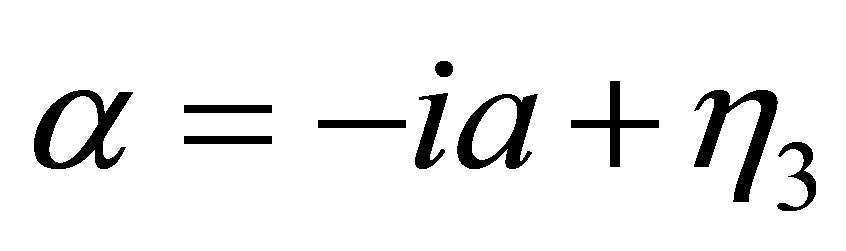 ,
, 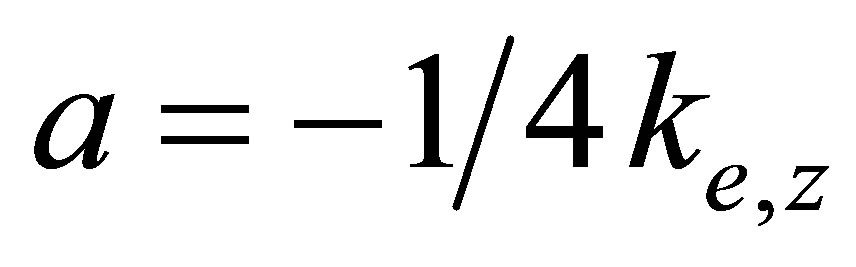 and
and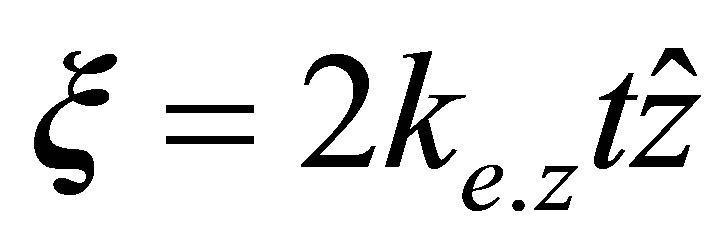 . Then performing the integral over the projectile co-ordinates, Equation (29) simplifies to
. Then performing the integral over the projectile co-ordinates, Equation (29) simplifies to
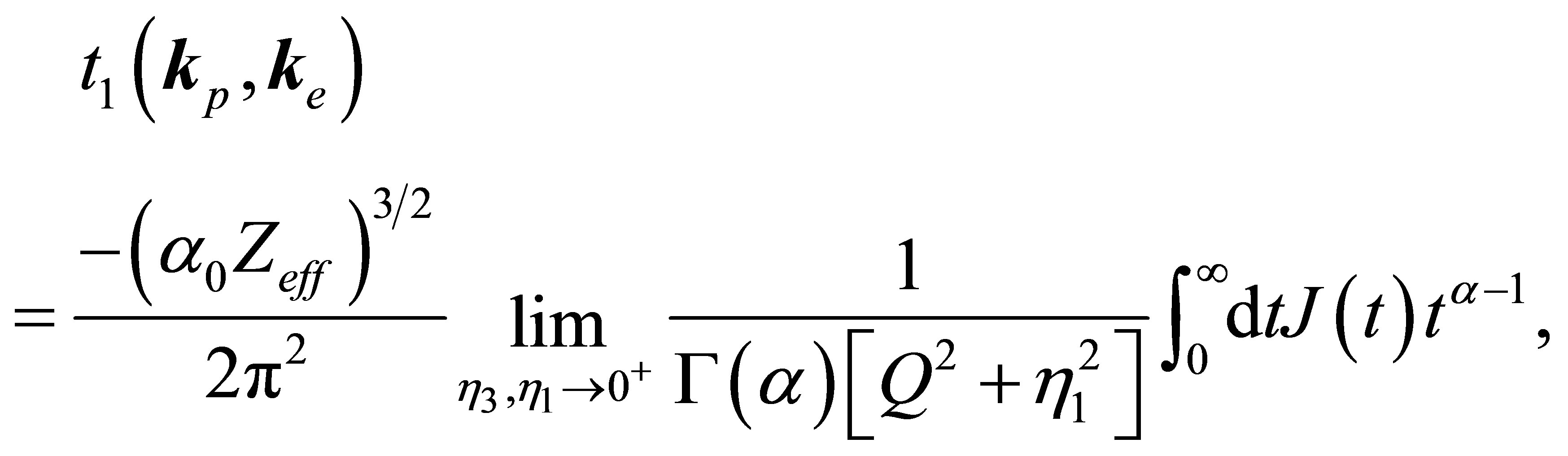 (32)
(32)
where
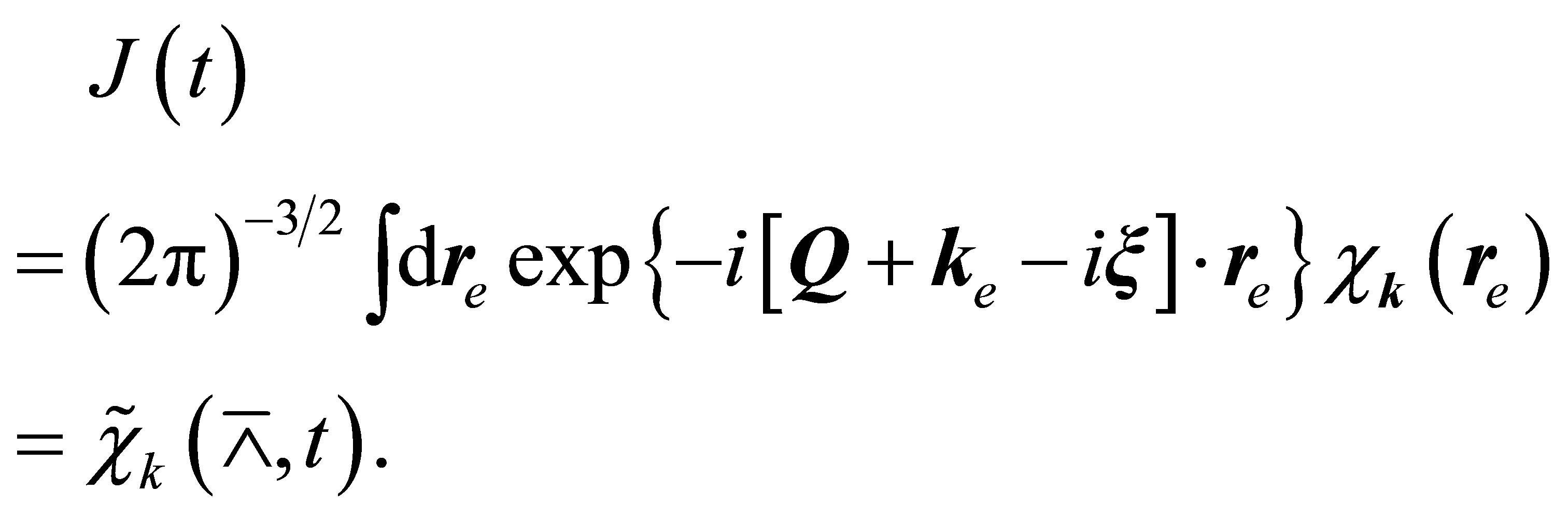 (33)
(33)
In Equation (33) we introduced the complex vector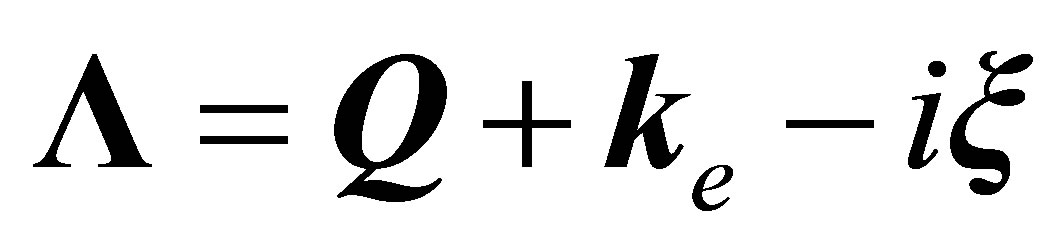 . Using the theory [23], we have
. Using the theory [23], we have
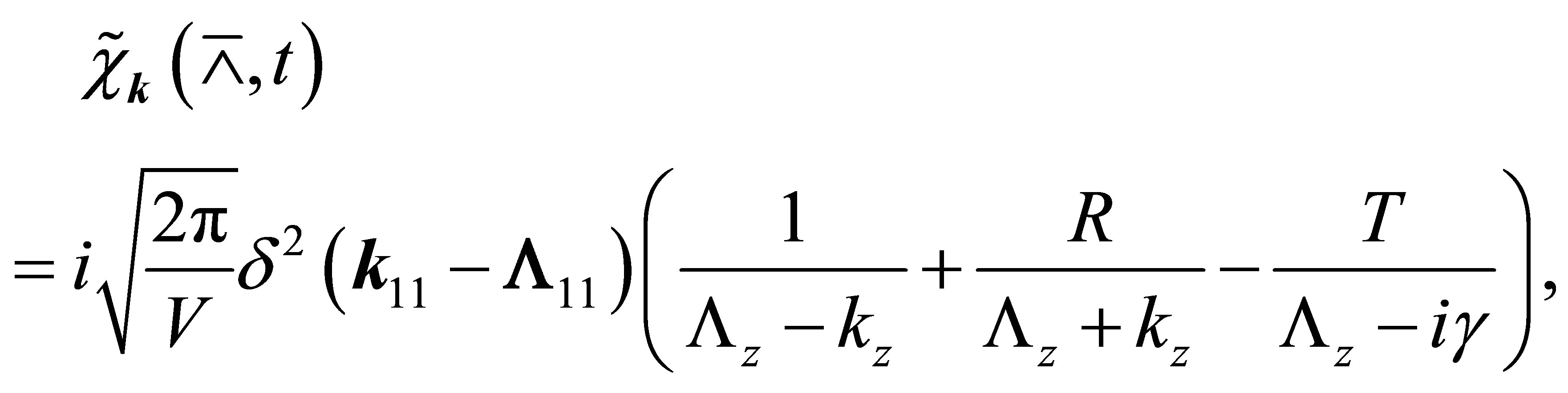 (34)
(34)
where the vector  is given by
is given by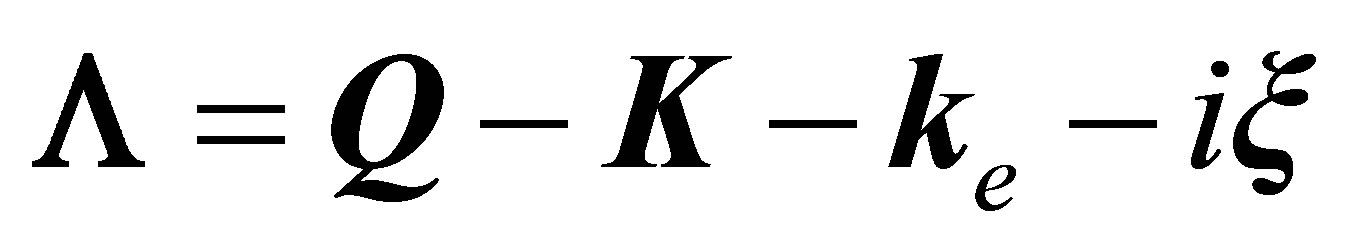 . By the Fourier transform
. By the Fourier transform 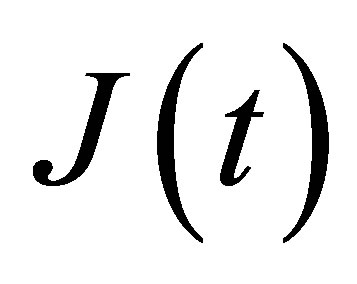 evaluates to
evaluates to
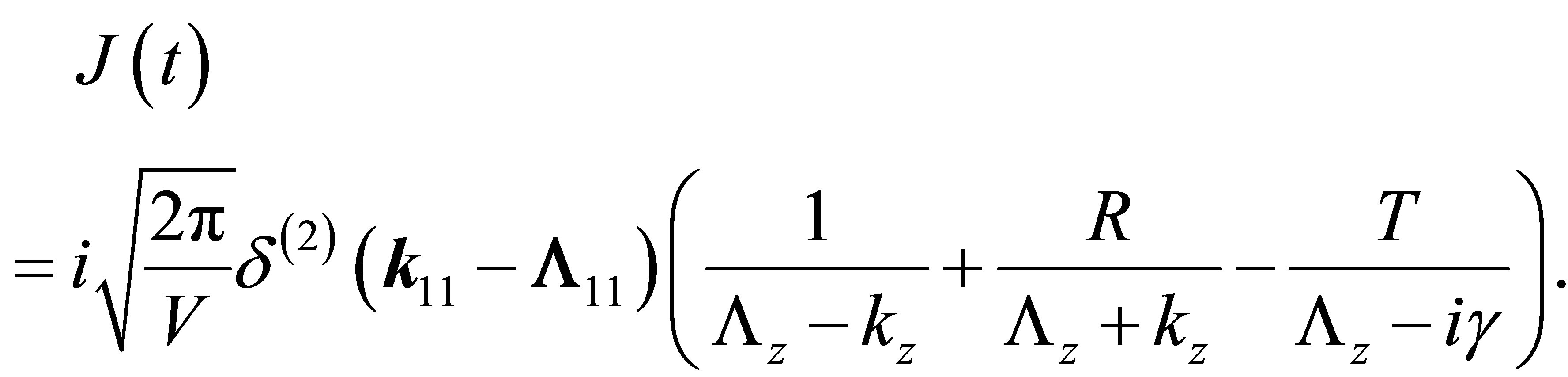 (35)
(35)
Now after inserting the Equation (35) into a Equation (32), the remaining one dimensional integral can be algebraically transformed to the Beta function integral representation
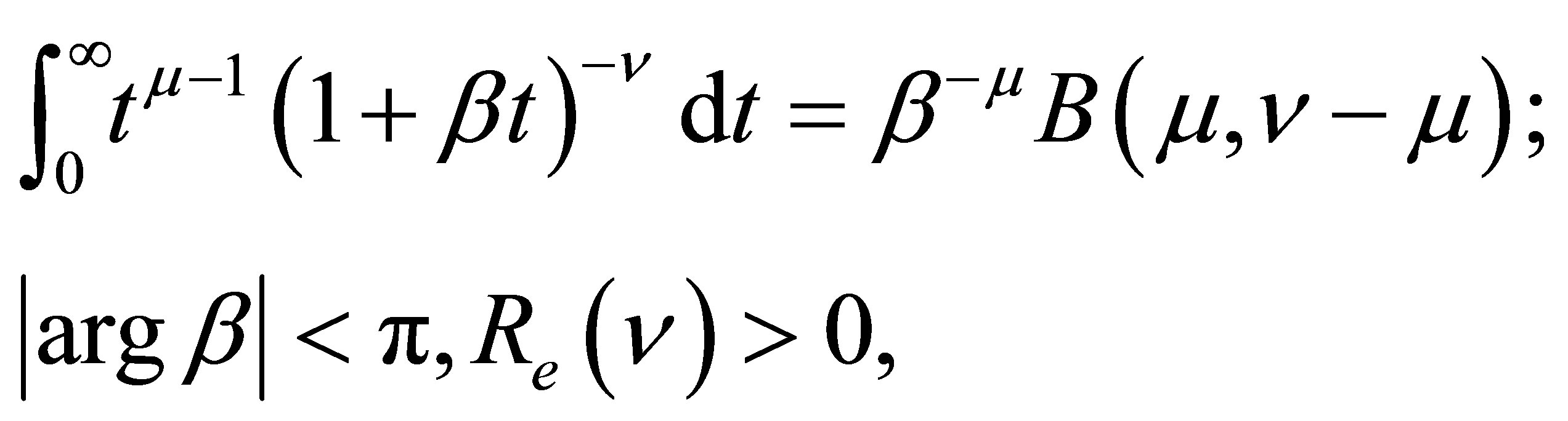 (36)
(36)
give
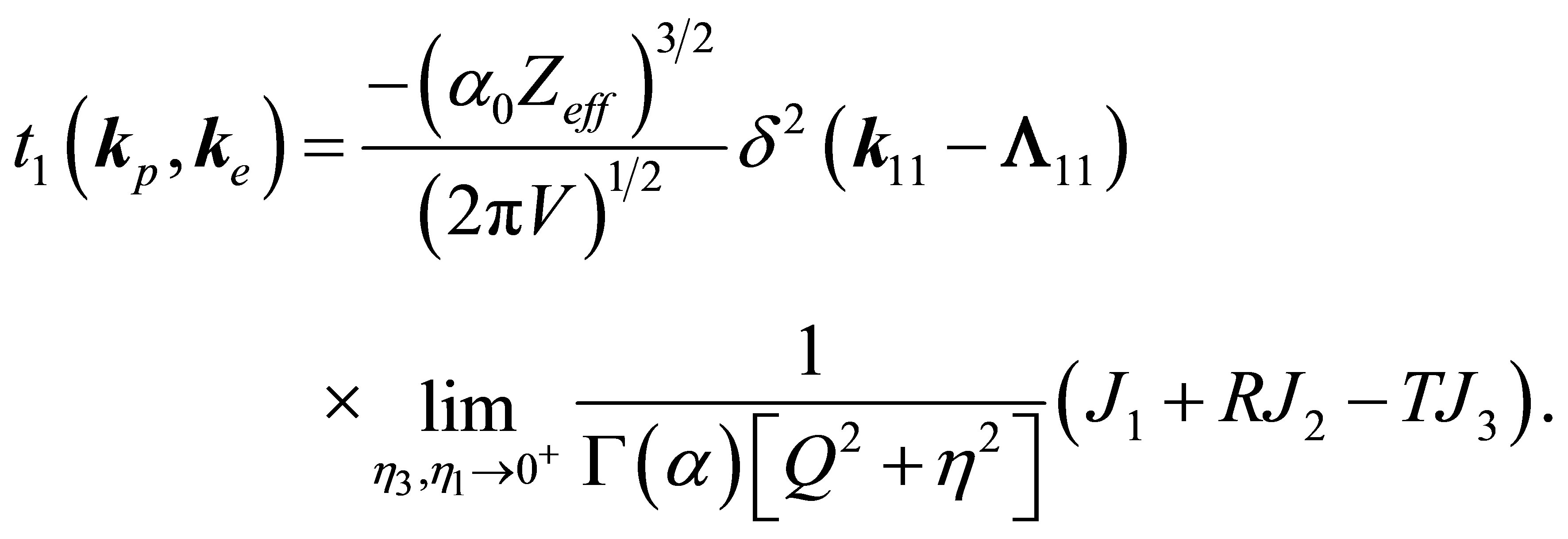 (37)
(37)
The functions 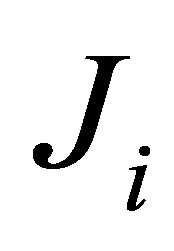 are given by
are given by
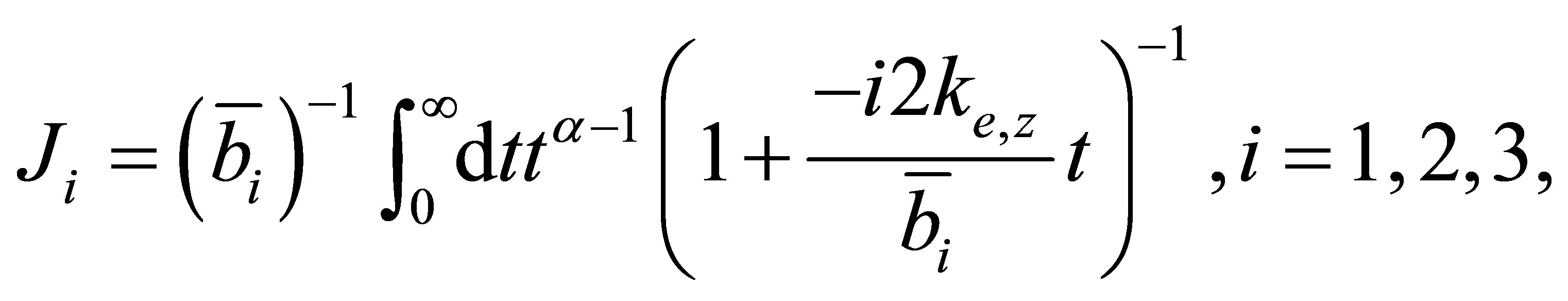 (38)
(38)
where
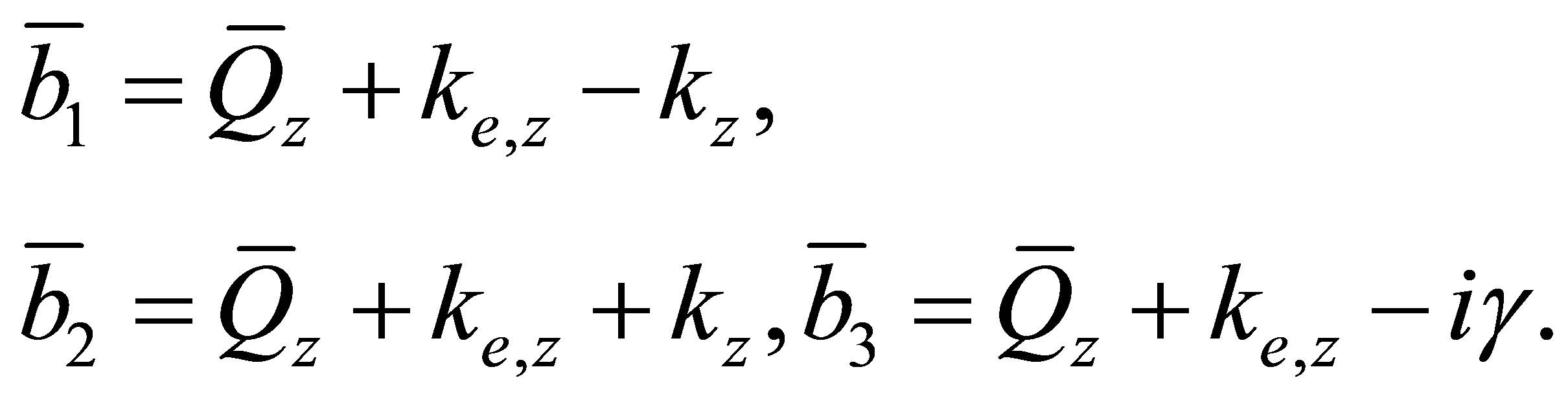 (39)
(39)
Making use Equation (36) and after calculation, the final expression
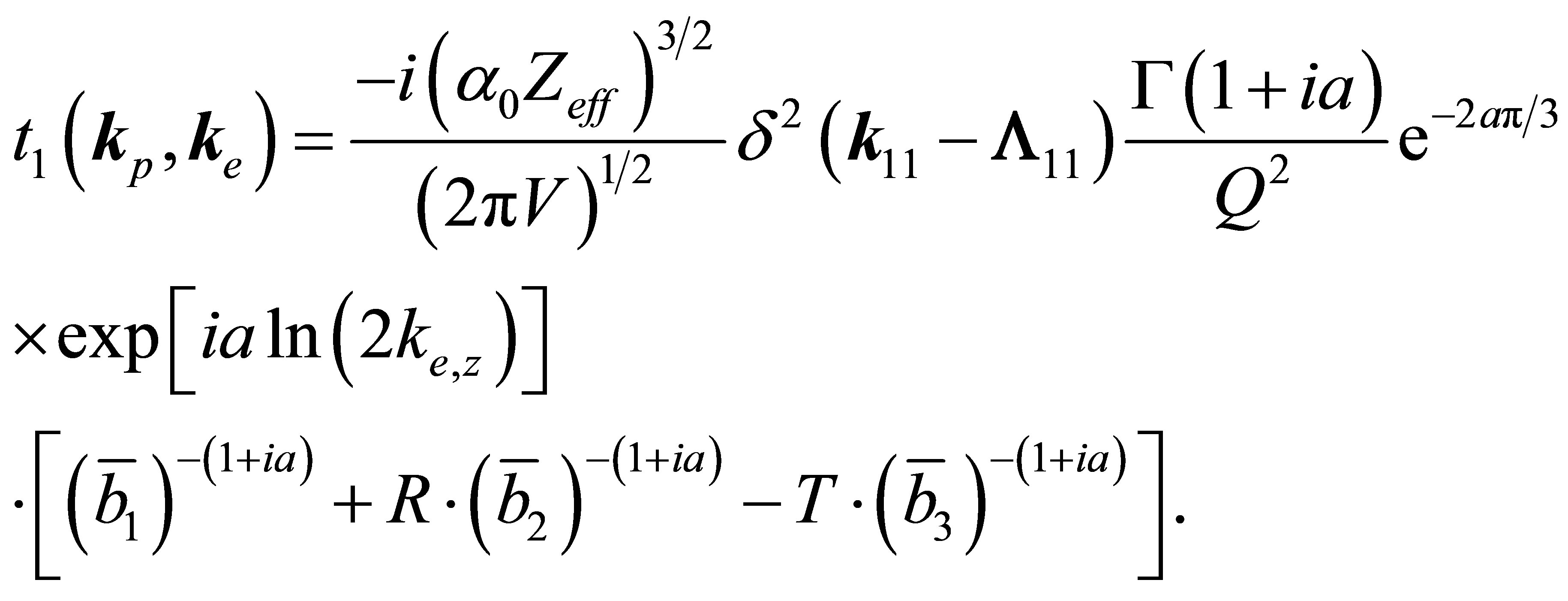 (40)
(40)
2.2. Analytical Calculation of the Transition Amplitude Term  in Relativistic Effects
in Relativistic Effects
In this case the transition amplitude term of the Equation (19), the screened Coulomb potential [26] for relativistic case is given by
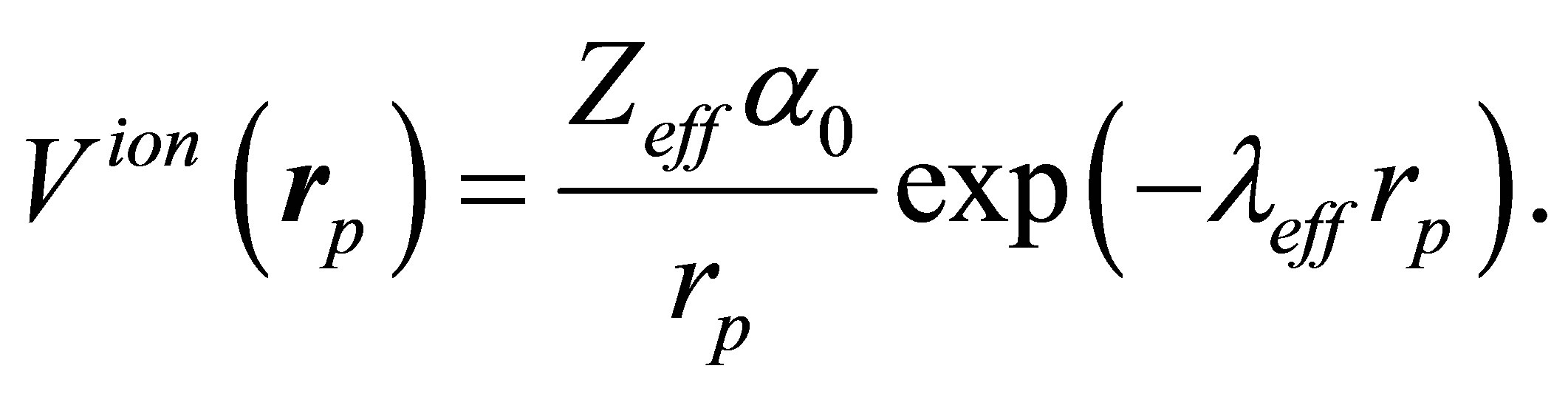 (41)
(41)
The effective parameter 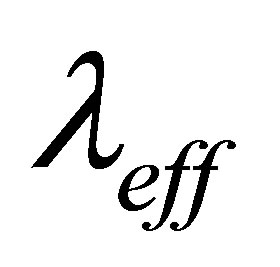 account for the screaming of the pure ionic field due to the presence of the localized positive cores as well as delocalized electrons [26]. For aluminum surface the numerical value of
account for the screaming of the pure ionic field due to the presence of the localized positive cores as well as delocalized electrons [26]. For aluminum surface the numerical value of 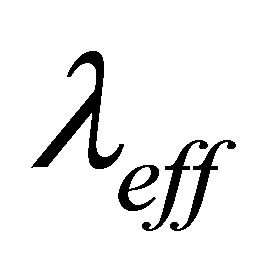 is 0.886. Equation (19) can be written as in semi-relativistic form
is 0.886. Equation (19) can be written as in semi-relativistic form
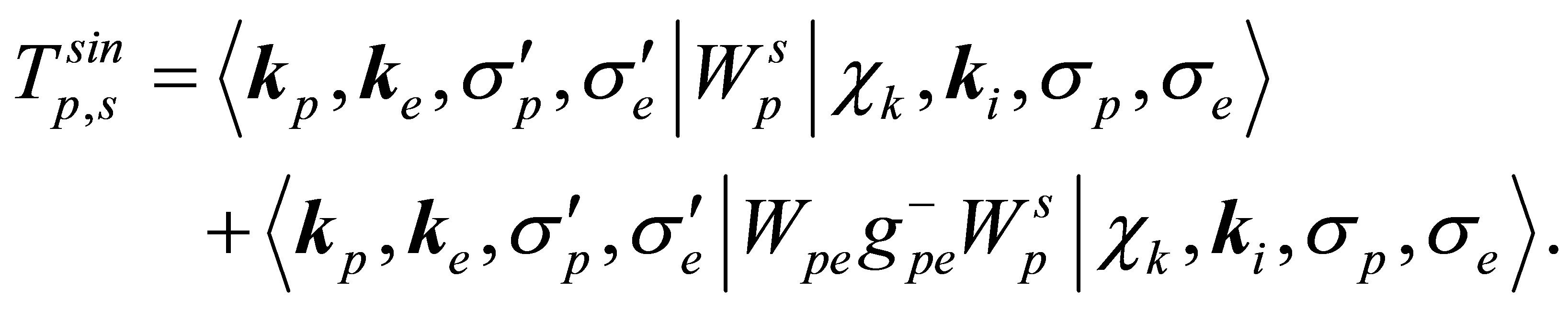 (42)
(42)
Here
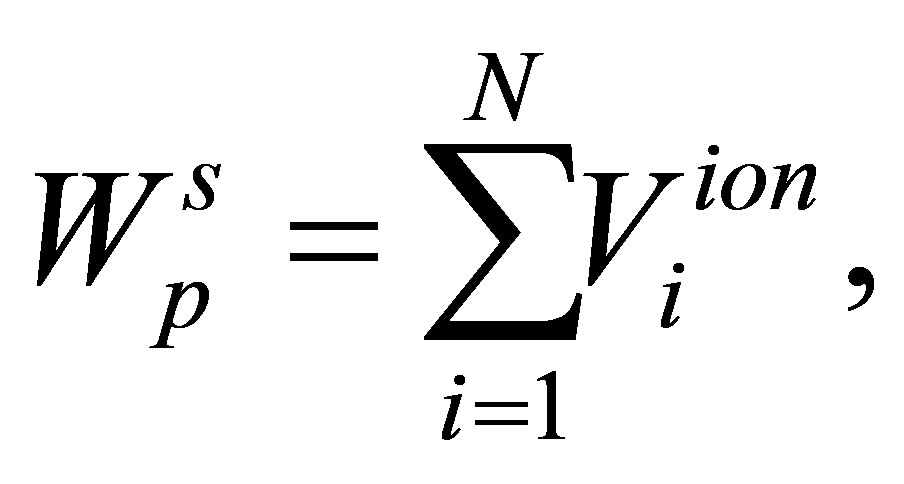 (43)
(43)
where 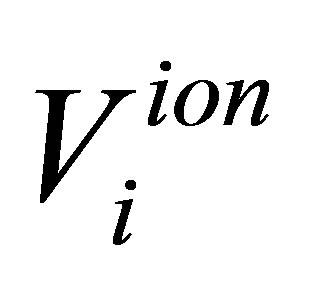 is the ionic core potential at the state
is the ionic core potential at the state , N is the number of ions in the solid and
, N is the number of ions in the solid and 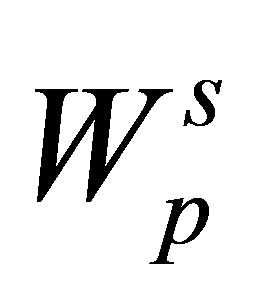 is periodic in each layer parallel to the x − y plane, but not in zdirections. The j-th ion in the
is periodic in each layer parallel to the x − y plane, but not in zdirections. The j-th ion in the 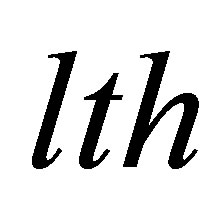 layer has the coordinates
layer has the coordinates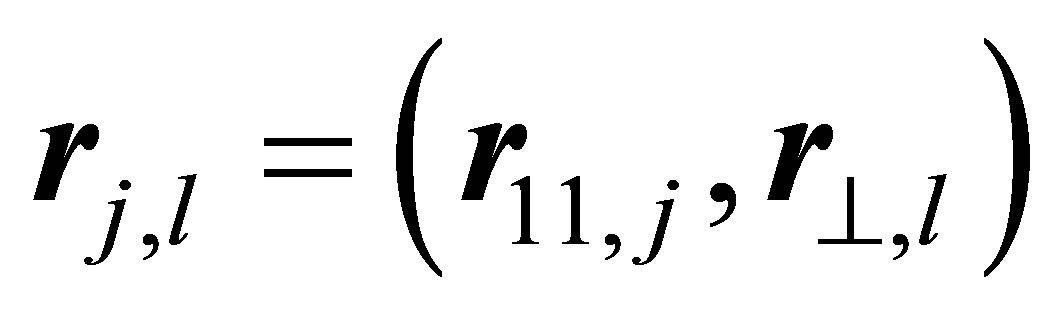 . Thus the periodic potential
. Thus the periodic potential 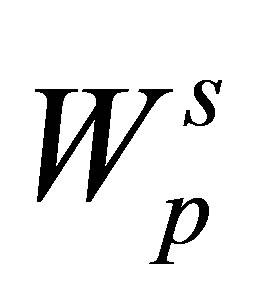 at the position
at the position 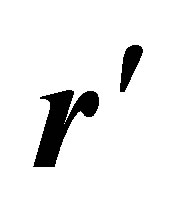 can be written as
can be written as
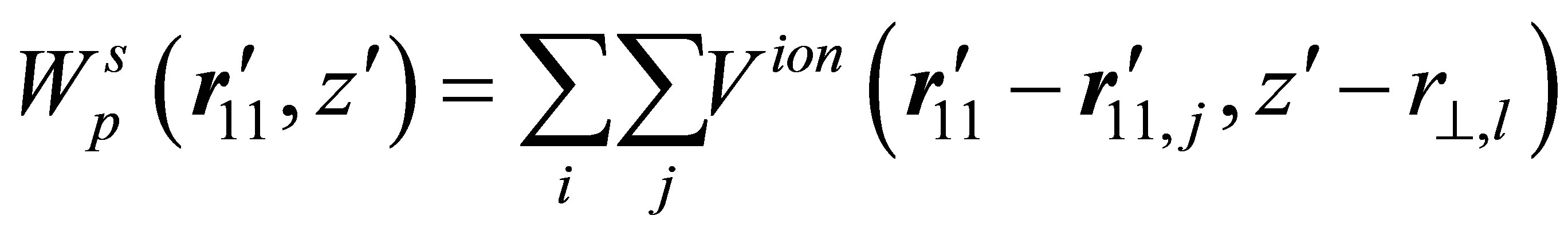 . (44)
. (44)
Since 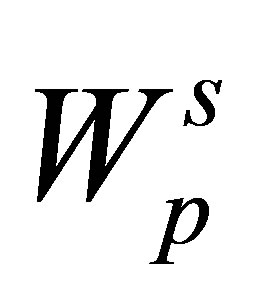 is periodic in the x and y directions, we can introduce [26] two dimensional reciprocal vectors
is periodic in the x and y directions, we can introduce [26] two dimensional reciprocal vectors 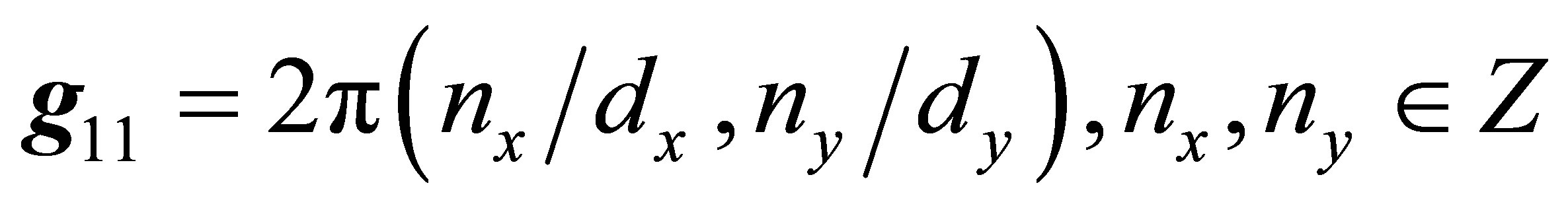 and write
and write 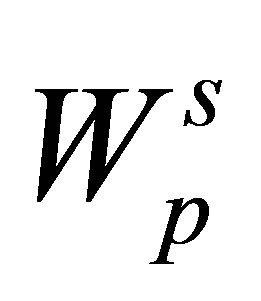 at the position
at the position 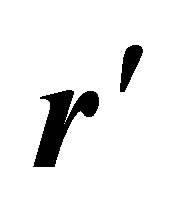 as
as
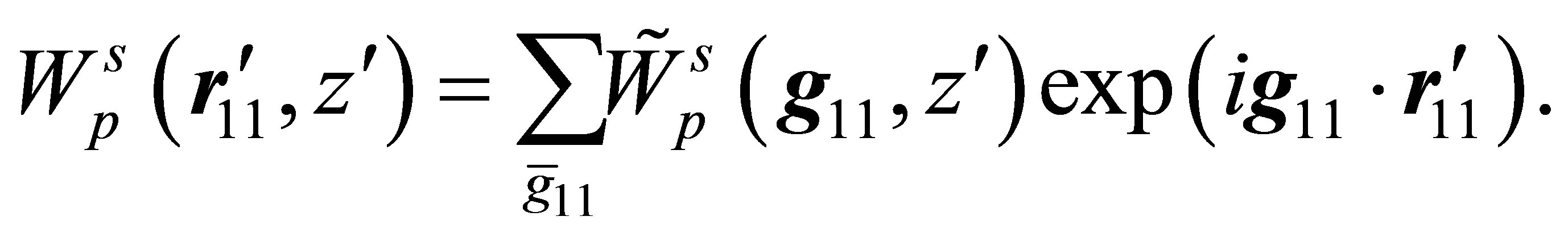 (45)
(45)
The two dimensional  Fourier transform
Fourier transform 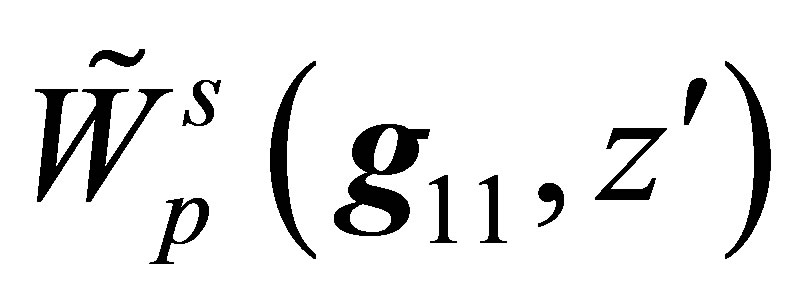 is given by
is given by
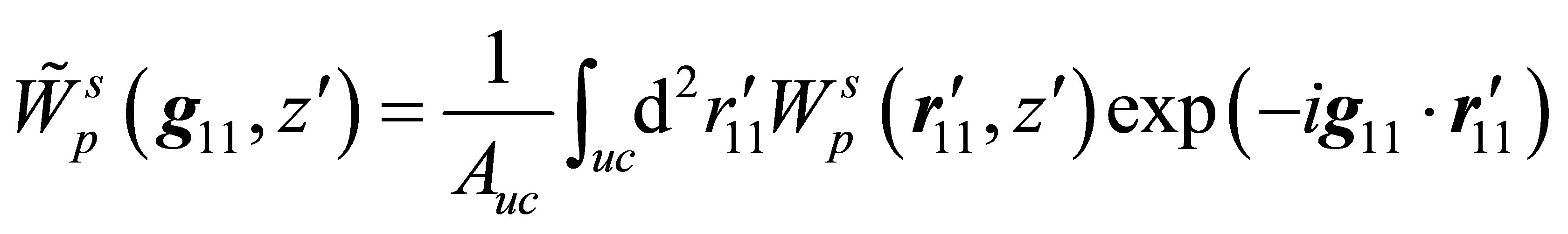 (46)
(46)
where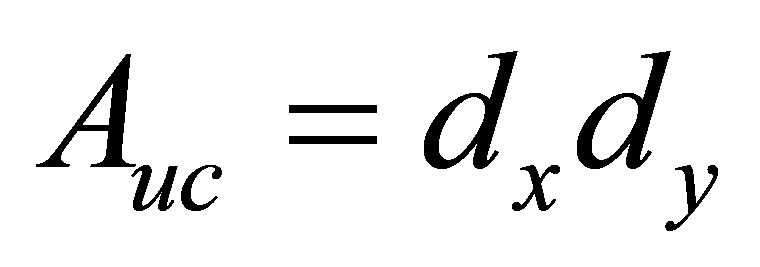 . The lattice constants in the x, y and z directions are
. The lattice constants in the x, y and z directions are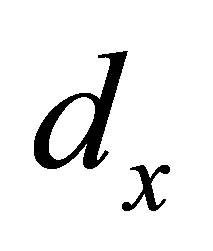 ,
, 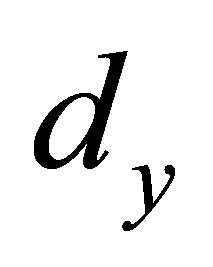 and
and 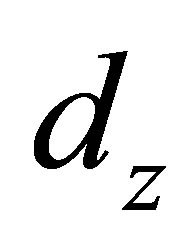 respectively.
respectively.
Using Equations (23), (24) and (42) the final expression for 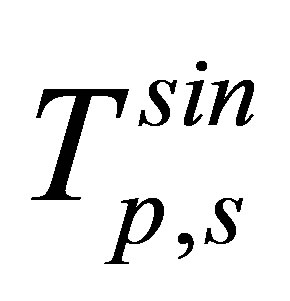 may be written as in the semi-relativistic form
may be written as in the semi-relativistic form
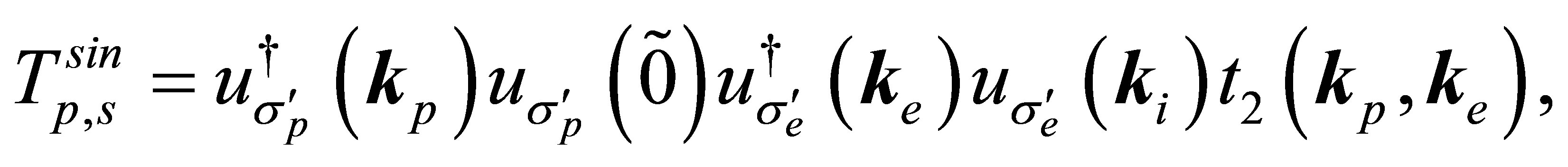 (47)
(47)
where
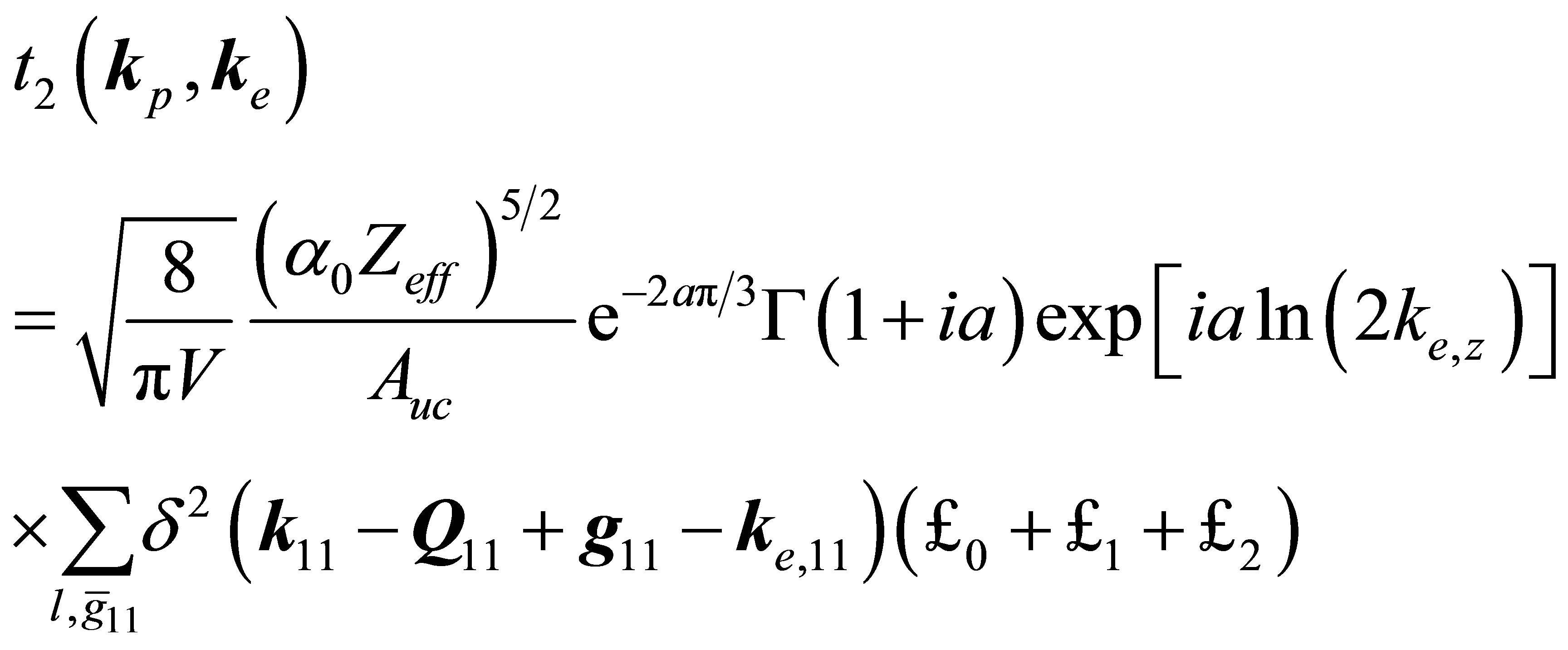 (48)
(48)
with
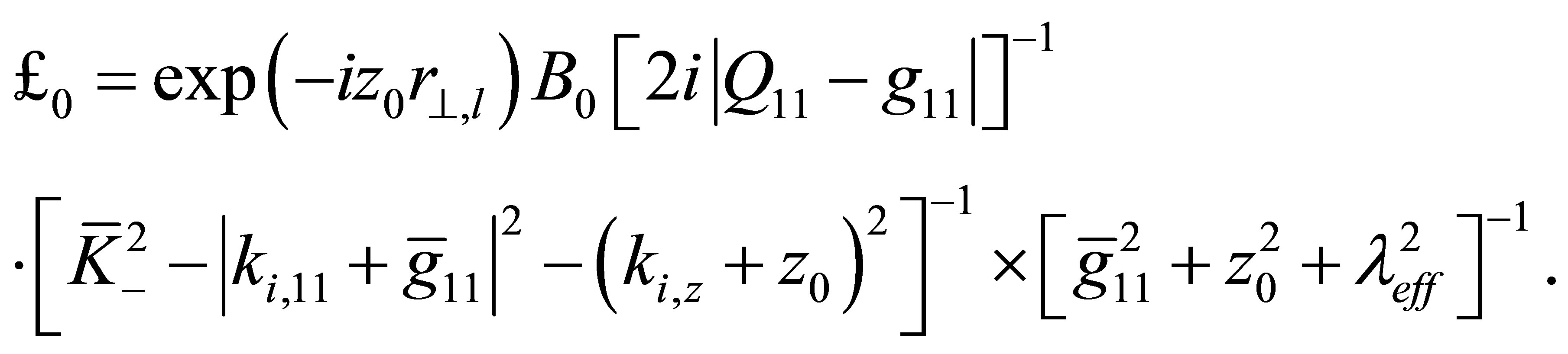 (49)
(49)
In case 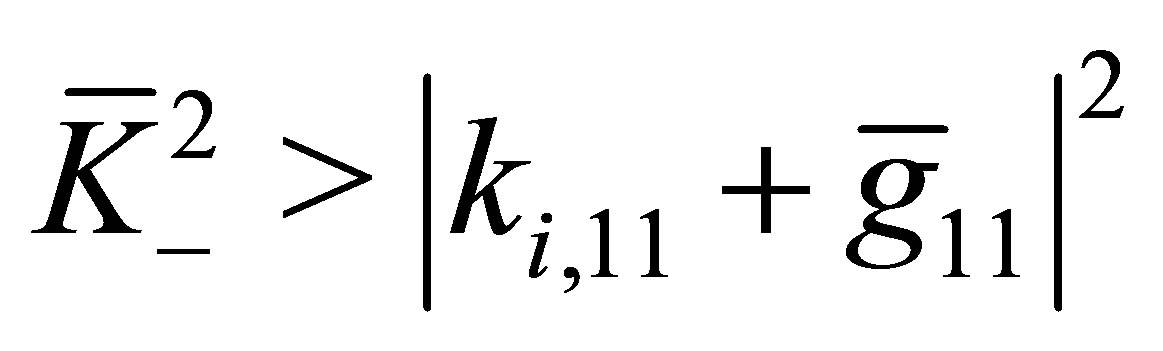 we obtain for
we obtain for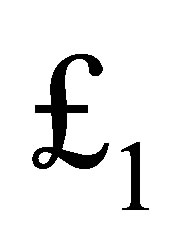 ,
,
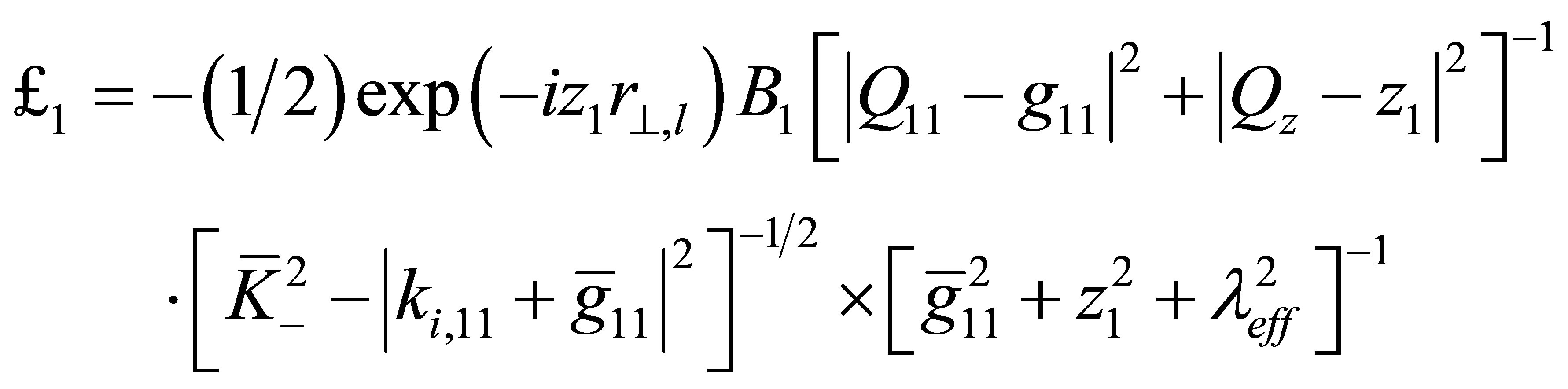 (50)
(50)
whereas if 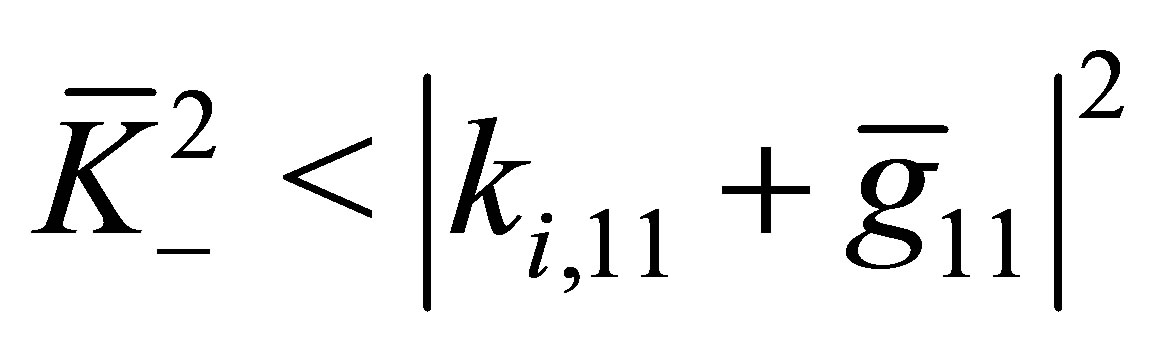 the following relation is valid:
the following relation is valid:
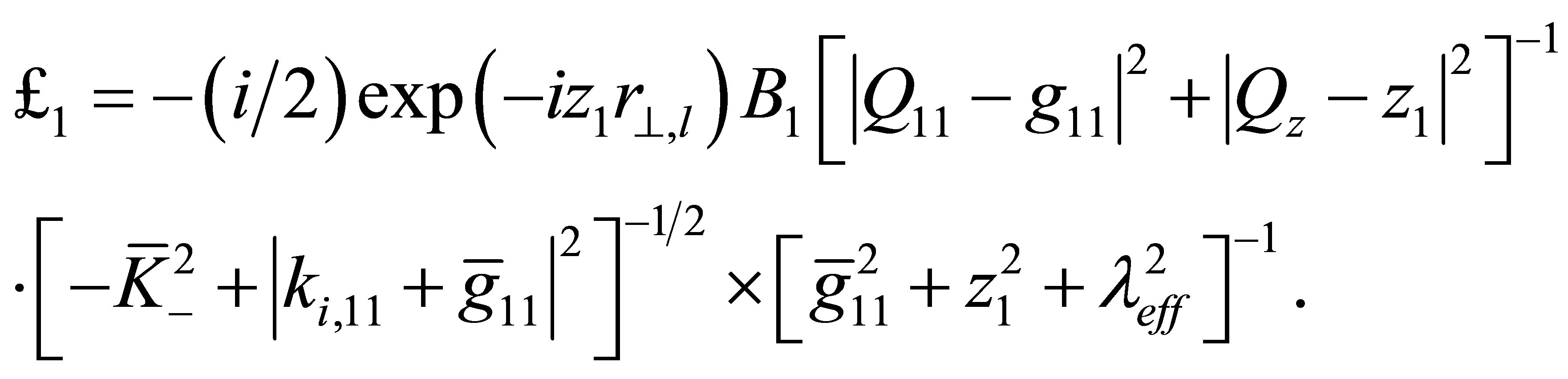 (51)
(51)
Also, the expression for 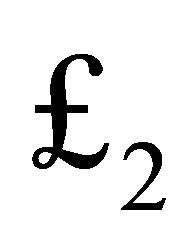 may be written as
may be written as
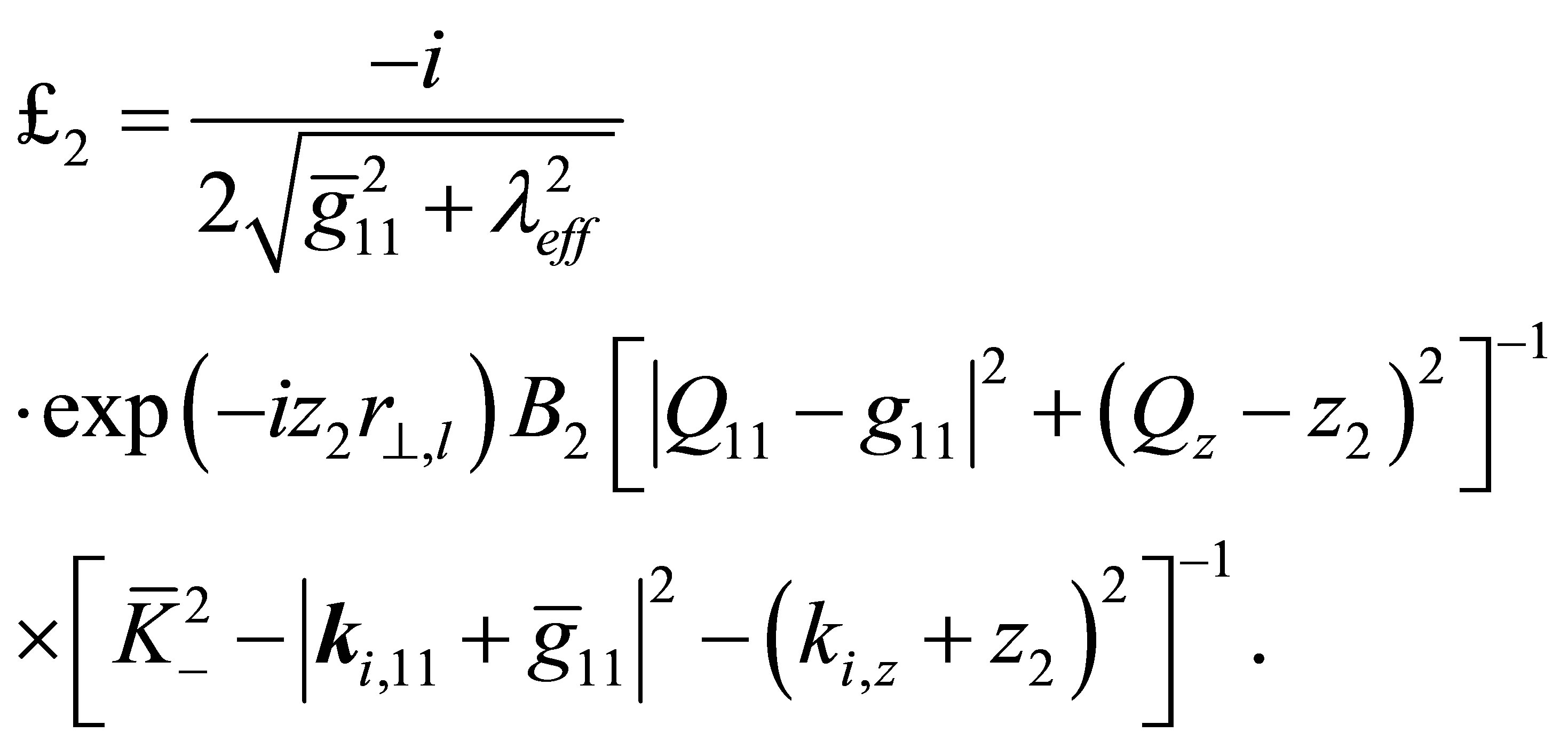 (52)
(52)
The function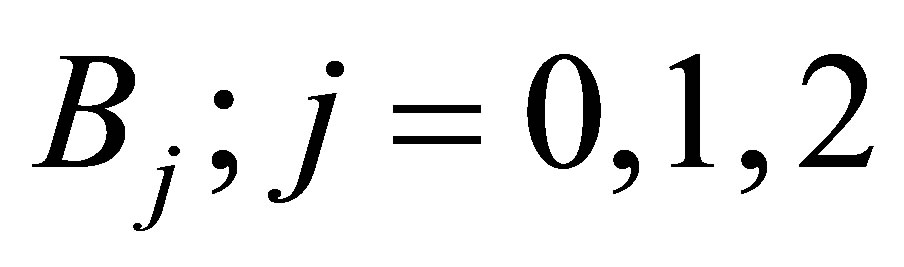 , we have been defined as
, we have been defined as
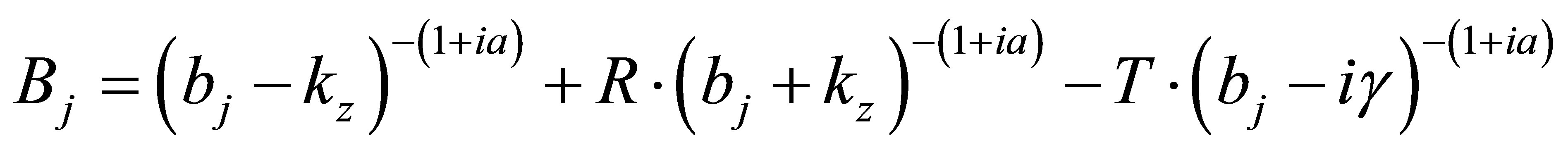 (53)
(53)
where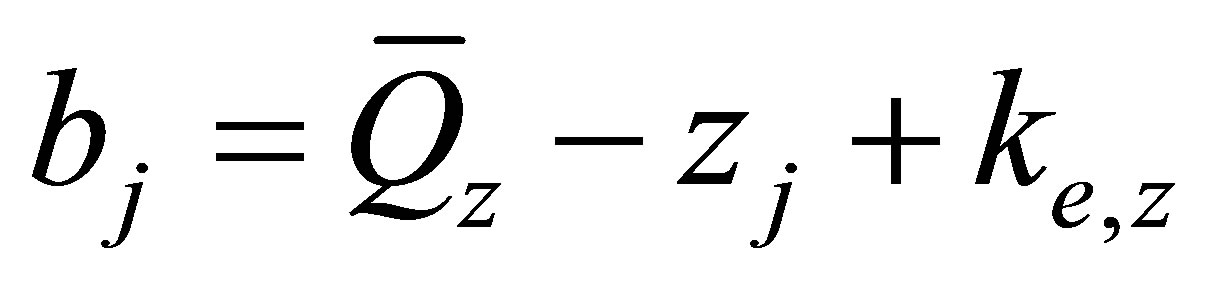 ,
, 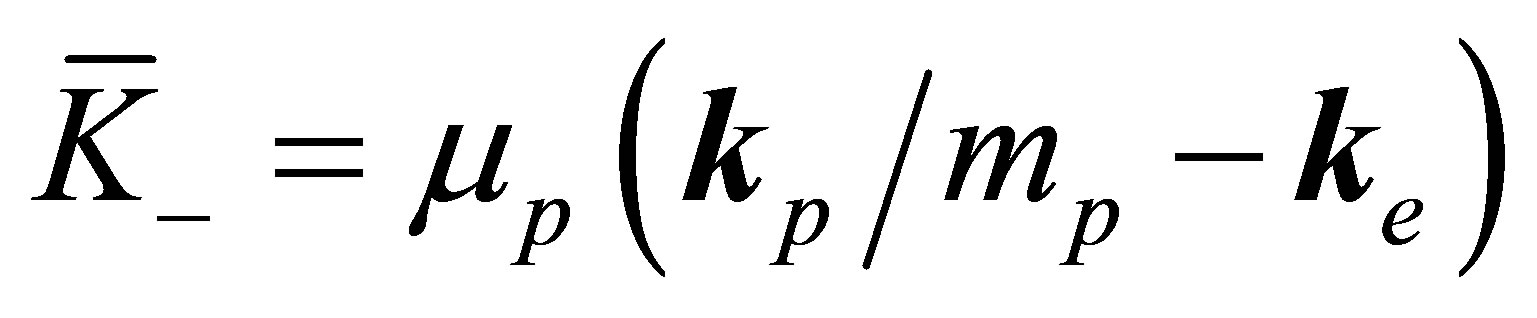 and
and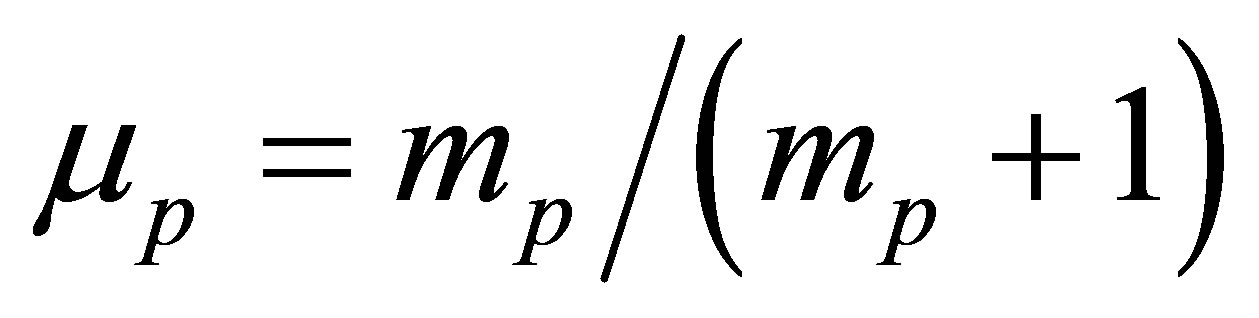 . Since
. Since 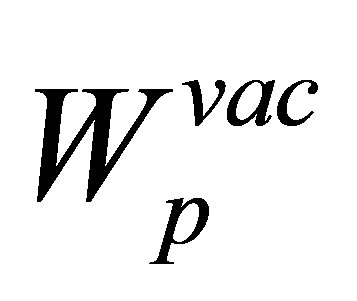 is an asymptotic (image charge ) perturbation, so the term
is an asymptotic (image charge ) perturbation, so the term 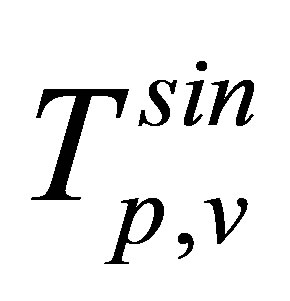 is neglected here. Therefore the expression for the
is neglected here. Therefore the expression for the 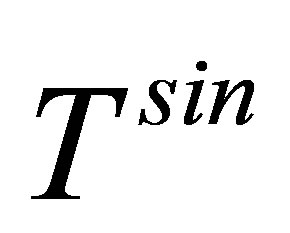 -matrix element may be written as in semi-relativistic form
-matrix element may be written as in semi-relativistic form
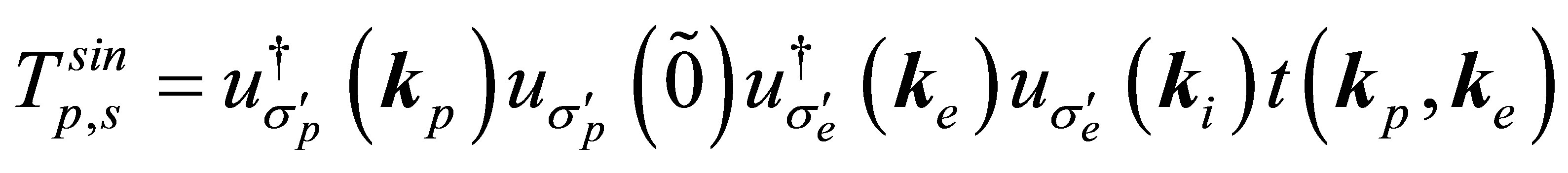 (54)
(54)
where
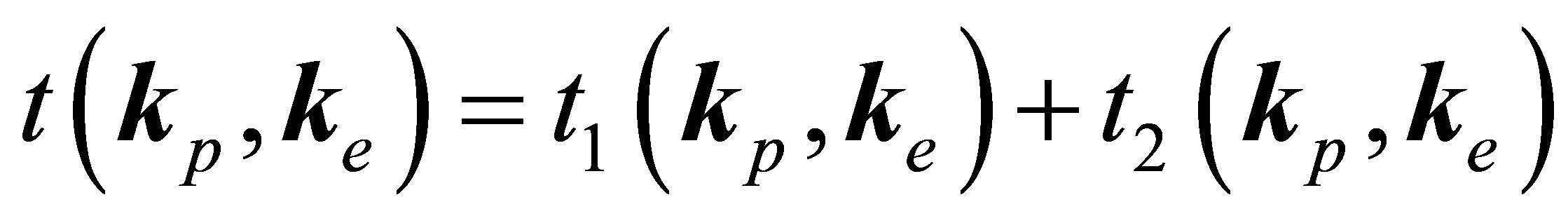 . (55)
. (55)
Now taking sum over final spin states and an average over initial states
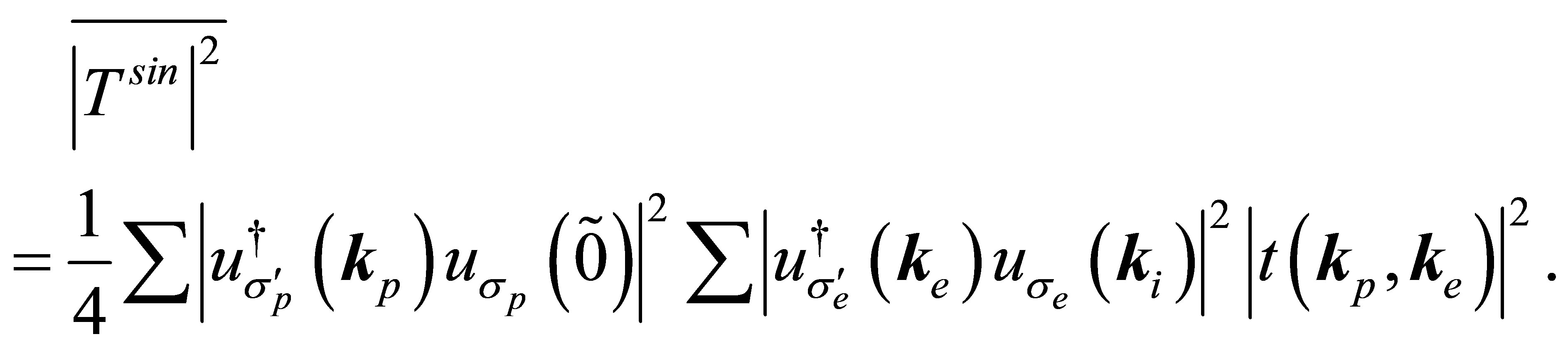 (56)
(56)
Now the spin sums can be obtained
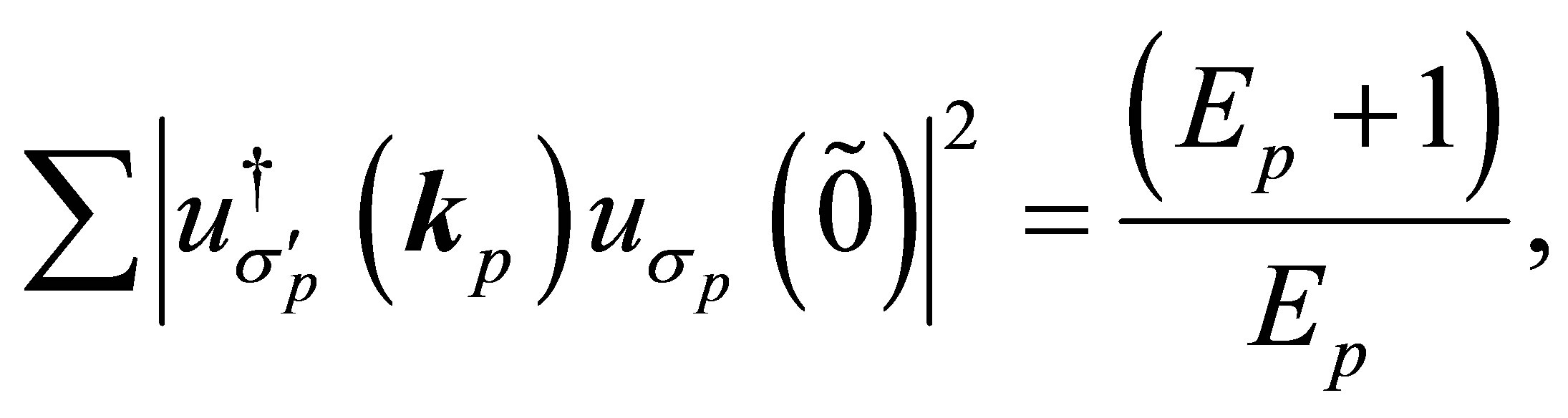 (57)
(57)
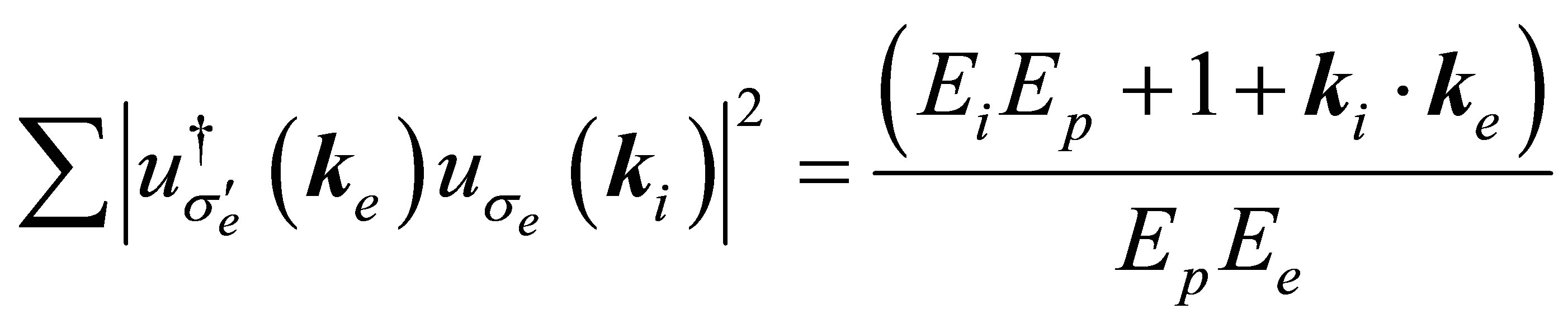 . (58)
. (58)
So, we obtain from Equation (56),
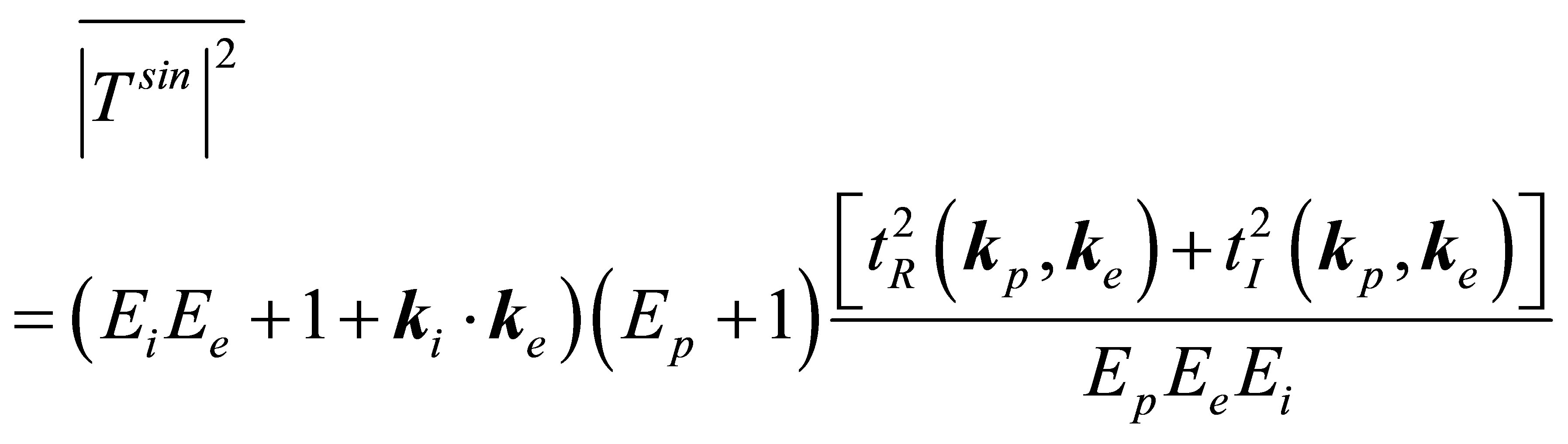 (59)
(59)
where 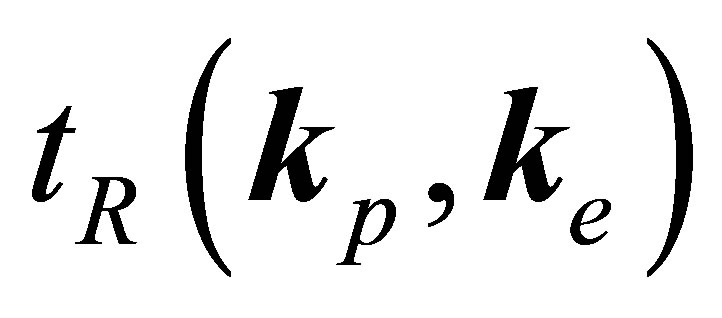 and
and 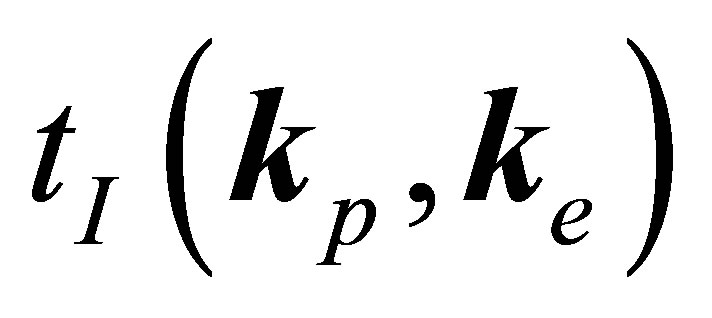 are the real and imaginary parts of the
are the real and imaginary parts of the 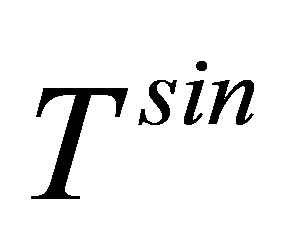 matrix element.
matrix element.
Finally, the differential cross-section [23] for 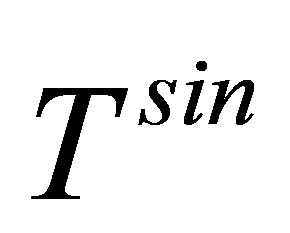 - matrix in semi-relativistic form is given by
- matrix in semi-relativistic form is given by
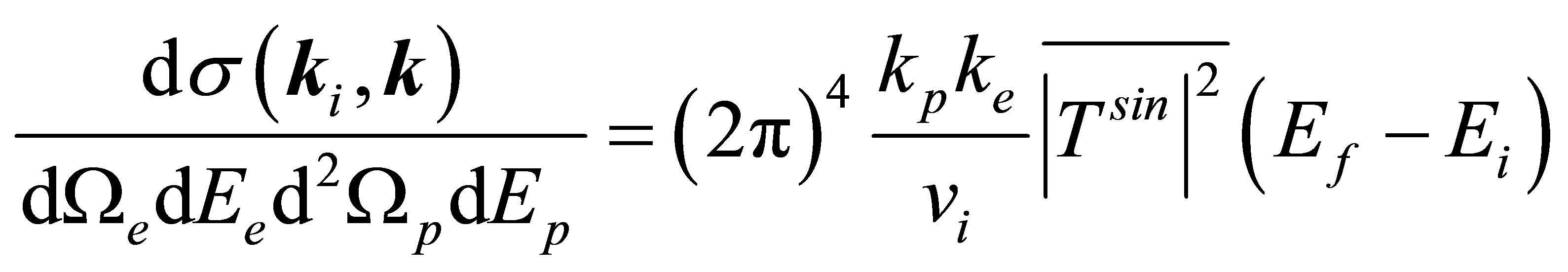 (60)
(60)
where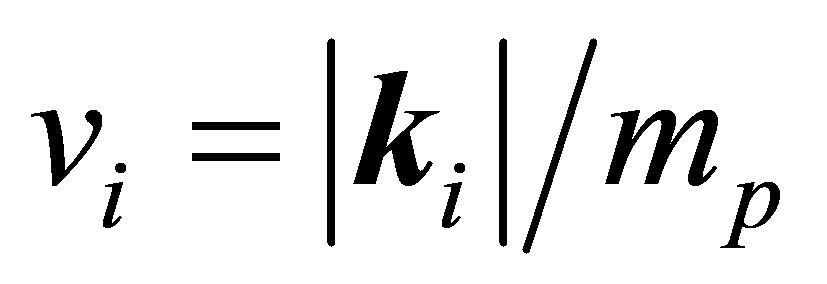 ,
, 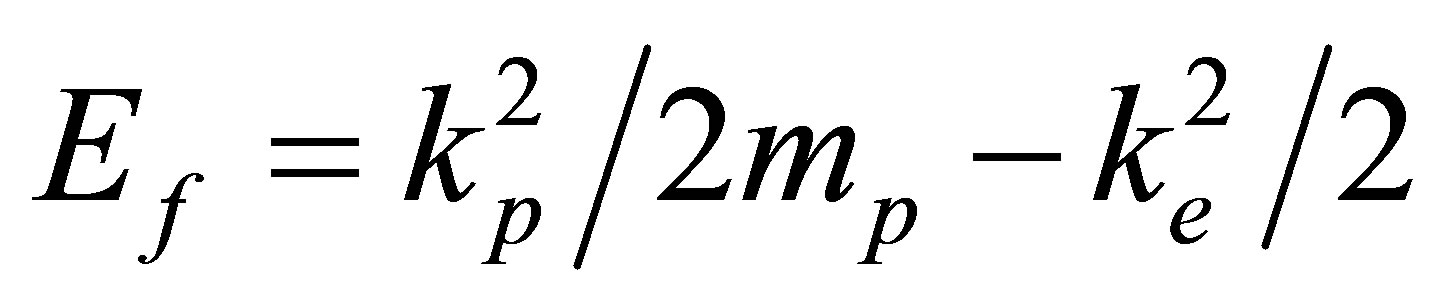 also
also 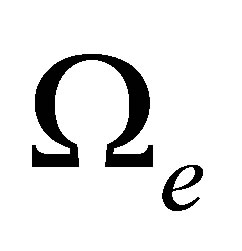 and
and 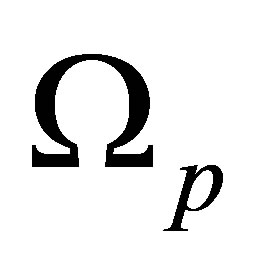 are the solid angles of the emitted electron and scattered projectile respectively.
are the solid angles of the emitted electron and scattered projectile respectively.
This is the modified formal theory on semi-relativistic effects during electron emission from metallic surfaces upon impact of high energy particles to determine differential cross-section of different kinematic conditions.
3. Concluding Remarks
A theoretical formulation of scattering cross-section of high energy change particles from clean metallic semiinfinite solid in the relativistic region has presented single scattering amplitude 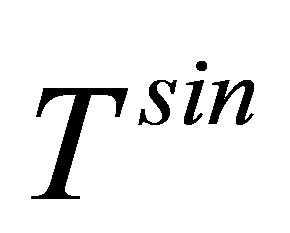 term [23]. In this theory, for multiply differential cross-sections, we used a semi-relativistic Jellium initial state wave function. A relativistic final state electron surface image charge interaction has been included in its asymptotic form. We will utilize another multiple scattering term
term [23]. In this theory, for multiply differential cross-sections, we used a semi-relativistic Jellium initial state wave function. A relativistic final state electron surface image charge interaction has been included in its asymptotic form. We will utilize another multiple scattering term 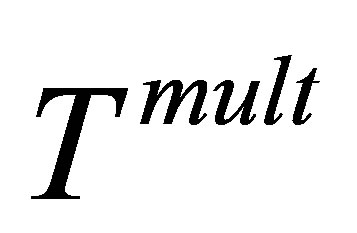 [23] which can provide better results for cross-section. Such analytical calculation and numerical results are in progress and will be reported in the next work.
[23] which can provide better results for cross-section. Such analytical calculation and numerical results are in progress and will be reported in the next work.
4. Acknowledgements
Part of this work was done when one of the authors (SD) was the DAAD Fellow at the institute of Physics, Martin-Luther University, Halle, Germany under Prof. Jamal Berakdar. This work also partially supported by Higher Education Quality Enhancement Program (HEQEP) of World Bank.
NOTES