Psychophysical Neuroeconomics of Decision Making: Nonlinear Time Perception Commonly Explains Anomalies in Temporal and Probability Discounting ()
1. Introduction
Canonical representations on Hermitian symmetric spaces  were introduced by Vershik-Gelfand-Graev [1] (for the Lobachevsky plane) and Berezin [2]. They are unitary with respect to some invariant non-local inner product (the Berezin form). Molchanov’s idea is that it is natural to consider canonical representations in a wider sense: to give up the condition of unitarity and let these representations act on sufficiently extensive spaces, in particular, on distributions. Moreover, the notion of canonical representation (in this wide sense) can be extended to other classes of semisimple symmetric spaces
were introduced by Vershik-Gelfand-Graev [1] (for the Lobachevsky plane) and Berezin [2]. They are unitary with respect to some invariant non-local inner product (the Berezin form). Molchanov’s idea is that it is natural to consider canonical representations in a wider sense: to give up the condition of unitarity and let these representations act on sufficiently extensive spaces, in particular, on distributions. Moreover, the notion of canonical representation (in this wide sense) can be extended to other classes of semisimple symmetric spaces , in particular, to para-Hermitian symmetric spaces, see [3]. Moreover, sometimes it is natural to consider several spaces
, in particular, to para-Hermitian symmetric spaces, see [3]. Moreover, sometimes it is natural to consider several spaces  together, possibly with different
together, possibly with different , embedded as open
, embedded as open  -orbits into a compact manifold
-orbits into a compact manifold , where
, where  acts, so that
acts, so that  is the closure of these orbits.
is the closure of these orbits.
Canonical representations can be constructed as follows. Let 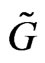 be a group containing
be a group containing  (an overgroup),
(an overgroup), 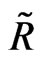 a series of representations of
a series of representations of 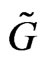 induced by characters of some parabolic subgroup
induced by characters of some parabolic subgroup  associated with
associated with  and acting on functions on
and acting on functions on . The canonical representations
. The canonical representations  of
of  are restrictions of
are restrictions of  to
to .
.
In this talk we carry out this program for para-Hermitian symmetric spaces of rank one. These spaces are exhausted up to the covering by spaces  with
with ,
, . For these spaces
. For these spaces , an overgroup is the direct product
, an overgroup is the direct product  and canonical representations turn out to be tensor products of representations of maximal degenerate series and contragredient representations. These tensor products are studied in [4], see also [5]. So we lean essentially on these papers [4,5]. We decompose canonical representations into irreducible constituents and decompose boundary representations. Notice that in our case the inverse of the Berezin transform
and canonical representations turn out to be tensor products of representations of maximal degenerate series and contragredient representations. These tensor products are studied in [4], see also [5]. So we lean essentially on these papers [4,5]. We decompose canonical representations into irreducible constituents and decompose boundary representations. Notice that in our case the inverse of the Berezin transform  can be easily written: precisely it is the Berezin transform
can be easily written: precisely it is the Berezin transform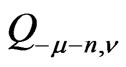 .
.
Canonical and boundary representations for 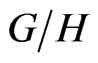 in the case
in the case  (then
(then  is the hyperboloid of one sheet in
is the hyperboloid of one sheet in ) were studied in [6]. For the two-sheeted hyperboloid in
) were studied in [6]. For the two-sheeted hyperboloid in , it was done in [7].
, it was done in [7].
In this paper we present only the main results. The detailed theory of canonical and boundary representations, for example, on a sphere with an action of the generalized Lorentz group, can be seen in [8].
Let us introduce some notation and agreements.
By 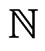 we denote
we denote . The sign
. The sign  denotes the congruence modulo 2.
denotes the congruence modulo 2.
For a character of the group  we shall use the following notation
we shall use the following notation

where ,
,  ,
, .
.
For a manifold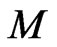 , let
, let  denote the Schwartz space of compactly supported infinitely differentiable
denote the Schwartz space of compactly supported infinitely differentiable  -valued functions on
-valued functions on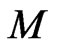 , with a usual topology, and
, with a usual topology, and  the space of distributions on
the space of distributions on —of anti-linear continuous functionals on
—of anti-linear continuous functionals on .
.
2. The Space  and the Manifold
and the Manifold 
We consider the symmetric space 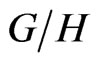 where
where ,
,  ,
,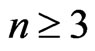 .
.
The group  acts on the space
acts on the space  by
by
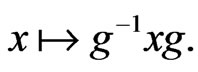
Let us write matrices in  in block form according to the partition
in block form according to the partition  of
of . Let us take the matrix
. Let us take the matrix

The subgroup 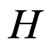 is just the stabilizer of this point
is just the stabilizer of this point , this subgroup consists of block diagonal matrices:
, this subgroup consists of block diagonal matrices:

Thus, our space 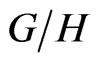 is the
is the  -orbit of
-orbit of , it consists of matrices of rank one and trace one.
, it consists of matrices of rank one and trace one.
Equip  with the standard inner product
with the standard inner product , let
, let . Let
. Let  be the sphere
be the sphere . Let
. Let  be the Euclidean measure on
be the Euclidean measure on . The group
. The group 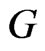 acts on
acts on  by
by .
.
Let 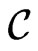 be a cone in
be a cone in  consisting of matrices
consisting of matrices  of rank one. Therefore, the space
of rank one. Therefore, the space  is the section of
is the section of  by the hyperplane
by the hyperplane .
.
Introduce a norm  in
in  by
by

where the prime denotes matrix transposition.
Let  be the section of
be the section of  by
by .
.
Define a map  by
by

It is a two-fold covering. The measure  defines a measure
defines a measure 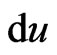 on
on  by
by

The action of the group  on
on  gives the following action of
gives the following action of  on
on :
:
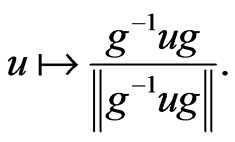
In particular, the subgroup , a maximal compact subgroup, acts on
, a maximal compact subgroup, acts on  by translations:
by translations:

Let us consider on  the function
the function
 (1)
(1)
The action on  has three orbits: namely, two open orbits (of dimension
has three orbits: namely, two open orbits (of dimension ):
):  and
and  and one orbit of dimension
and one orbit of dimension :
:  . The orbit
. The orbit  is a Stiefel manifold, it is the boundary of
is a Stiefel manifold, it is the boundary of . Denote
. Denote . Each of orbits
. Each of orbits  can be identified with the space
can be identified with the space . The map is constructed by means of generating lines of the cone
. The map is constructed by means of generating lines of the cone .
.
3. Maximal Degenerate Series Representations
Recall [4] maximal degenerate series representations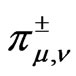 ,
,  ,
, 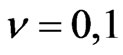 , of the group
, of the group . Let
. Let  be the subspace of
be the subspace of  consisting of functions
consisting of functions 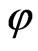 of parity
of parity :
: . The representations
. The representations  act on
act on  by
by

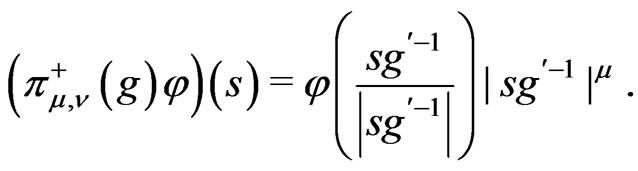
4. Representations of  Associated with
Associated with 
Recall [5] a series of representations 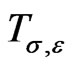 of the group
of the group  associated with the space
associated with the space .
.
Denote by  the space of functions
the space of functions 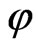 in
in  of parity
of parity :
:

The representation  acts on
acts on  by
by
 (2)
(2)
Let  denote the following sesqui-linear form
denote the following sesqui-linear form
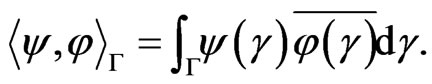 (3)
(3)
Define an operator  on
on  by
by

It intertwines 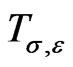 and
and . The operator
. The operator 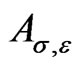 is a meromorphic function of
is a meromorphic function of . Let us normalize this operator (multiplying it by a function of
. Let us normalize this operator (multiplying it by a function of ) such that the normalized operator
) such that the normalized operator  is an entire non-vanishing function of
is an entire non-vanishing function of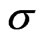 .
.
There are three series of unitarizable irreducible representations. The continuous series consists of  with
with ,
, 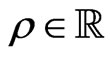 , the inner product is (3). The complementary series consists of
, the inner product is (3). The complementary series consists of  with
with
 , the inner product is
, the inner product is 
with a factor. The discrete series consists of the representations  where
where ,
,
 ,
,  , which are factor representations of
, which are factor representations of
 on the quotient spaces
on the quotient spaces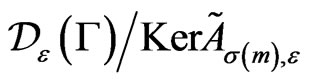 . The representations
. The representations  with the same
with the same  and different
and different
 are equivalent. It is convenient to take
are equivalent. It is convenient to take  where
where  for odd
for odd  and
and  for even
for even . The inner product is induced by the form
. The inner product is induced by the form .
.
5. Canonical Representations
We define canonical representations ,
,  ,
,  , of the group
, of the group  as tensor products:
as tensor products:

They can be realized on : let
: let  denote the subspace of
denote the subspace of  consisting of functions
consisting of functions  of parity
of parity :
: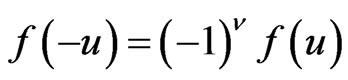 , then the representation
, then the representation  acts on
acts on 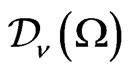 by a formula similar to (2):
by a formula similar to (2):

The inner product
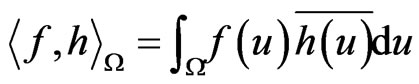 (4)
(4)
is invariant with respect to the pair , i.e.
, i.e.
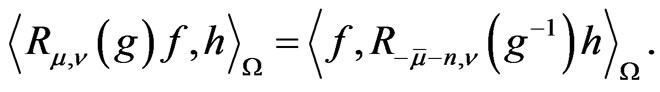 (5)
(5)
Consider an operator  on
on 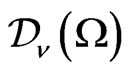 defined by
defined by

It turns out that the composition 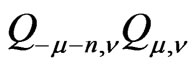 is equal to the identity operator
is equal to the identity operator  up to a factor. We can take
up to a factor. We can take  such that
such that
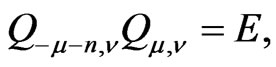
namely,

With the form (4) the operator  interacts as follows:
interacts as follows:
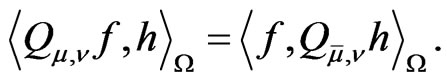 (6)
(6)
This operator  intertwines the representations
intertwines the representations  and
and , i.e.
, i.e.

Let us call it the Berezin transform.
Let  be the space of distributions on
be the space of distributions on  of parity
of parity . We extend
. We extend 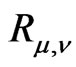 and
and 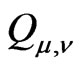 to
to  by (5) and (6) respectively and retain their names and the notation.
by (5) and (6) respectively and retain their names and the notation.
Let us introduce the following Hermitian form  on
on :
:

Let us call this form the Berezin form.
6. Boundary Representations
The canonical representation  gives rise to two representations
gives rise to two representations  and
and  associated with the boundary
associated with the boundary  of the manifolds
of the manifolds  (boundary representations). The first one acts on distributions concentrated at
(boundary representations). The first one acts on distributions concentrated at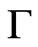 , the second one acts on jets orthogonal to
, the second one acts on jets orthogonal to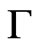 .
.
We can introduce “polar coordinates” on  corresponding to the foliation of
corresponding to the foliation of  into
into 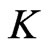 -orbits. The
-orbits. The  - orbits are level surfaces of the function
- orbits are level surfaces of the function , see (1). For
, see (1). For  the
the  -orbits are diffeomorphic to
-orbits are diffeomorphic to . In these coordinates the measure
. In these coordinates the measure  on
on  is
is

where  is the measure on
is the measure on .
.
Let  be a function in
be a function in . Consider it as a function of polar coordinates. Consider its Taylor series
. Consider it as a function of polar coordinates. Consider its Taylor series  in powers of
in powers of . Here
. Here 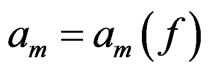 are functions in
are functions in . Denote by
. Denote by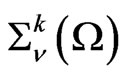 ,
,  ,
,  , the space of distributions in
, the space of distributions in , having the form
, having the form

where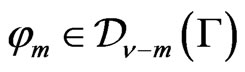 ,
,  is the Dirac delta function on the real line,
is the Dirac delta function on the real line,  its derivatives. Let
its derivatives. Let  .
.
Denote by  Taylor coefficients of the function
Taylor coefficients of the function
 . The distribution
. The distribution 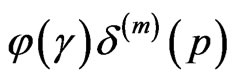 acts on a function
acts on a function 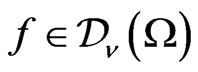 as follows:
as follows:
 (7)
(7)
Denote by  the restriction of
the restriction of  to
to . This representation is written as a upper triangular matrix with the diagonal
. This representation is written as a upper triangular matrix with the diagonal ,
, .
.
Distributions in 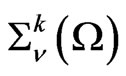 can be extended in a natural way to a space wider than
can be extended in a natural way to a space wider than . Namely, let
. Namely, let 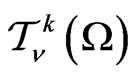
be the space of functions  of class
of class  on
on  and
and  of parity
of parity  and having the Taylor decomposition of order
and having the Taylor decomposition of order :
:

where . Then (7) keeps for
. Then (7) keeps for  with
with .
.
Let 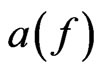 denote the column of Taylor coefficients
denote the column of Taylor coefficients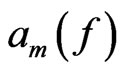 . The representation
. The representation  acts on these columns:
acts on these columns:

It is written as a lower triangular matrix with the diagonal ,
, .
.
The boundary representations 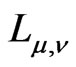 and
and  are in a duality.
are in a duality.
7. Poisson and Fourier Transforms
Let us write operators  and
and 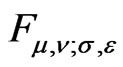 intertwining representations
intertwining representations  and
and . We call them Poisson and Fourier transforms associated with canonical representations.
. We call them Poisson and Fourier transforms associated with canonical representations.
The Poisson transform  is a map
is a map 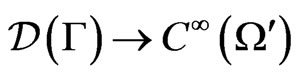 given by
given by

It intertwines  with
with . Here we consider
. Here we consider
 as the restriction to
as the restriction to  of the representation
of the representation  acting on distributions in
acting on distributions in .
.
For a  -finite function
-finite function  and
and  the Poisson transform has the following decomposition in powers of
the Poisson transform has the following decomposition in powers of :
:

where 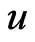 has polar coordinates
has polar coordinates . Here
. Here  and
and
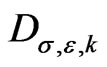 are certain operators acting on
are certain operators acting on . The factors
. The factors  and
and  give poles of the Poisson transform in
give poles of the Poisson transform in  depending on
depending on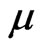 :
:
 (8)
(8)
where  and
and ,
,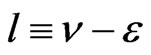 . If a pole belongs only to one of series (8), then the pole is simple, and if a pole belongs to both series (8), then
. If a pole belongs only to one of series (8), then the pole is simple, and if a pole belongs to both series (8), then 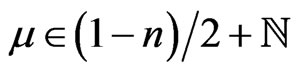 and the pole is of the second or first order.
and the pole is of the second or first order.
Let the pole ,
,  , be simple. The residue
, be simple. The residue 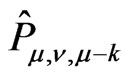 of
of  at this pole is an operator
at this pole is an operator
 . Denote the image of this operator by
. Denote the image of this operator by .
.
The Fourier transform  is a map
is a map  given by
given by

It intertwines  with
with .
.
The Fourier and Poisson transforms are conjugate to each other:

Poles in 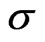 of the Fourier transform are situated at points
of the Fourier transform are situated at points
 (9)
(9)
where  and
and ,
, . If a pole belongs only to one of the series (9), then the pole is simple, and if a pole belongs to both series (9), then
. If a pole belongs only to one of the series (9), then the pole is simple, and if a pole belongs to both series (9), then  and the pole is of the second or first order.
and the pole is of the second or first order.
Let the pole ,
,  , be simple.
, be simple.
The residue 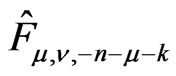 of
of  at this pole is a “boundary” operator
at this pole is a “boundary” operator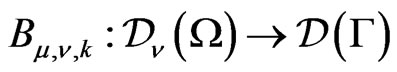 ,
, . The operator
. The operator 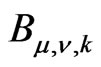 is defined in terms of Taylor coefficients
is defined in terms of Taylor coefficients : it is a linear combination of functions
: it is a linear combination of functions . Therefore, we may consider the following operator
. Therefore, we may consider the following operator  acting on columns
acting on columns
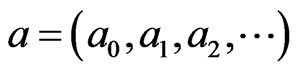 of functions
of functions : this operator to any column
: this operator to any column  assigns the column
assigns the column
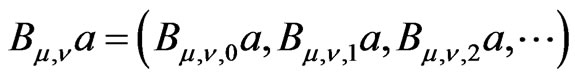 of functions in the same space
of functions in the same space —by the same formulas without
—by the same formulas without . This operator
. This operator  is given by a lower triangular matrix.
is given by a lower triangular matrix.
8. Decomposition of Boundary Representations
The meromorphic structure of the Poisson and Fourier transforms is a basis for decompositions of boundary representations  and
and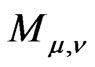 .
.
Let the pole  of the Poisson transform is simple, in particular, it happens when
of the Poisson transform is simple, in particular, it happens when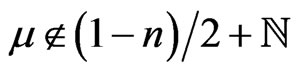 . Then the boundary representation
. Then the boundary representation  is diagonalizable which means that
is diagonalizable which means that  decomposes into the direct sum of
decomposes into the direct sum of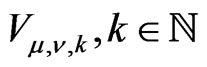 , and the restriction of
, and the restriction of 
to  is equivalent to
is equivalent to  (by means of
(by means of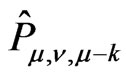 ).
).
If a pole is of the second order, then the decomposition of 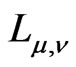 contains a finite number of Jordan blocks, this number depends on
contains a finite number of Jordan blocks, this number depends on .
.
Let the pole 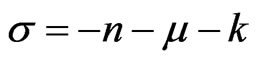 of the Fourier transform is simple, in particular, when
of the Fourier transform is simple, in particular, when . Then the matrix
. Then the matrix 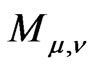 is diagonalizable which means that
is diagonalizable which means that
 is a diagonal matrix. Its diagonal is
is a diagonal matrix. Its diagonal is ,
, .
.
If a pole is of the second order, then the decomposition of  contains a finite number of Jordan blocks, this number depends on
contains a finite number of Jordan blocks, this number depends on .
.
9. Decomposition of Canonical Representations
Let us write decomposition of canonical representations. We restrict ourselves to a generic case:  lies in strips
lies in strips

Case (A): .
.
Theorem 1 Let . Then the canonical representation
. Then the canonical representation 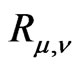 decomposes—as the quasiregular representation [5]—into irreducible unitary representations of continuous and discrete series with multiplicity one. Namely, let us assign to a function
decomposes—as the quasiregular representation [5]—into irreducible unitary representations of continuous and discrete series with multiplicity one. Namely, let us assign to a function 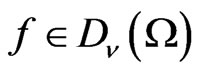 the family of its Fourier components
the family of its Fourier components ,
,  ,
,  ,
,  , and
, and
 ,
, . This correspondence is
. This correspondence is  equivariant. There is an inversion formula:
equivariant. There is an inversion formula:
 (10)
(10)
and a “Plancherel formula” for the Berezin form:
 (11)
(11)
Here  and
and  stand for the Plancherel measure for
stand for the Plancherel measure for , see [5], the factor
, see [5], the factor  is given by following formula:
is given by following formula:

Case (B):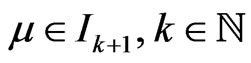 .
.
Here we continue decomposition (10) analytically in  from
from  to
to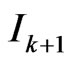 ,
, . Some poles in
. Some poles in 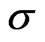 of the integrand intersect the integrating line—the line
of the integrand intersect the integrating line—the line 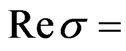
 . They are poles
. They are poles  and
and 
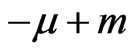 of the Poisson transform with
of the Poisson transform with . They give additional summands to the right hand side. So after the continuation we obtain:
. They give additional summands to the right hand side. So after the continuation we obtain:
 (12)
(12)
where the integral and the series mean the same as in (10) and

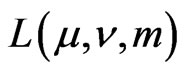 are some numbers.
are some numbers.
Similarly, the continuation of (11) gives
 (13)
(13)
where the integral and the series mean the same as in (11) and  are some numbers.
are some numbers.
The operators ,
,  , can be extended from
, can be extended from
 to the space
to the space  and therefore to the sum
and therefore to the sum

Then these operators  turn out to be projection operators onto
turn out to be projection operators onto . Moreover, there are some “orthogonality relations” for them. Decomposition (13) can also be extended to the space
. Moreover, there are some “orthogonality relations” for them. Decomposition (13) can also be extended to the space . This decomposition is a “Pythagorean theorem” for decomposition (12).
. This decomposition is a “Pythagorean theorem” for decomposition (12).
Theorem 2 Let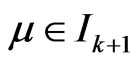 ,
, . Then the space
. Then the space  has to be completed to
has to be completed to . On this space the representation
. On this space the representation  splits into the sum of two terms: the first one decomposes as
splits into the sum of two terms: the first one decomposes as  does in Case (A), the second one decomposes into the sum of
does in Case (A), the second one decomposes into the sum of  irreducible representations
irreducible representations ,
, . Namely, let us assign to any
. Namely, let us assign to any  the family
the family

where ,
,  ,
,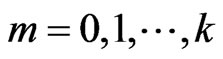 . This correspondence is
. This correspondence is  -equivariant. There is an inverse formula, see (12), and a “Plancherel formula”, see (13).
-equivariant. There is an inverse formula, see (12), and a “Plancherel formula”, see (13).
Case (C): .
.
Now we continue decomposition (10) analytically in  from
from  to
to . Here poles
. Here poles  and
and ,
,  ,
,  , of the integrand (they are poles of the Fourier transform) give additional terms. We obtain
, of the integrand (they are poles of the Fourier transform) give additional terms. We obtain
 (14)
(14)
where the integral and the series mean the same as in (10) and

 some numbers. The operators
some numbers. The operators  can be extended to the space
can be extended to the space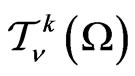 ,
, . Denote by
. Denote by  the image of
the image of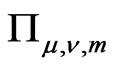 . It turns out that the operators
. It turns out that the operators  are projection operators onto
are projection operators onto  and for them there are some “orthogonality relations”.
and for them there are some “orthogonality relations”.
Now we continue decomposition (11) from  to
to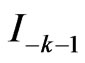 . Poles of the integrand which intersect the integrating line
. Poles of the integrand which intersect the integrating line  and give additional terms (they are poles of both Fourier transforms) turn out fortunately to be of the first order, since at these points the function
and give additional terms (they are poles of both Fourier transforms) turn out fortunately to be of the first order, since at these points the function 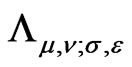 as a function of
as a function of  has zero of the first order. After the continuation we obtain:
has zero of the first order. After the continuation we obtain:
 (15)
(15)
where the integral and the series mean the same as in (11), 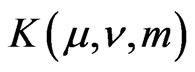 some numbers. It is a “Pythagorean theorem” for decomposition (14).
some numbers. It is a “Pythagorean theorem” for decomposition (14).
Theorem 3 Let ,
, . Then the representation
. Then the representation  considered on the space
considered on the space  splits into the sum of two terms. The first one acts on the subspace of functions
splits into the sum of two terms. The first one acts on the subspace of functions  such that their Taylor coefficients
such that their Taylor coefficients 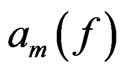 are equal to 0 for
are equal to 0 for  and decomposes as
and decomposes as  does in Case (A), the second one decomposes into the direct sum of
does in Case (A), the second one decomposes into the direct sum of  irreducible representations
irreducible representations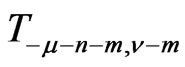 ,
, 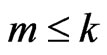 acting on the sum of the spaces
acting on the sum of the spaces . There is an inversion formula, see (14), and a “Plancherel formula” for the Berezin form, see (15).
. There is an inversion formula, see (14), and a “Plancherel formula” for the Berezin form, see (15).