Spectral Geometric Triangle Properties of Chlorophyll-A Inversion in Taihu Lake Based on TM Data ()
1. Introduction
In recent years, many coastal and inland waters have become enriched with nutrients and now support excessive increases in the chlorophyll-a concentration [1]. Remote sensing technology has been proposed as a useful means to improve the capability of estimating the chlorophyll-a concentration accurately [2-4]. It is well known that the water optical properties can provide quantitative information on the optically significant materials presented in water bodies. The bands ranging from 400 nm to 750 nm are most commonly used to estimate the chlorophyll-a concentration [5-9].
A variety of algorithms have been developed for estimating the chlorophyll-a concentration in Case I water, including empirical and semi-analytical models [7,10,11]. Most of these algorithms were based on the spectral properties near the region of 700 nm. Another widely applied parameter was the ratio of the near-infrared peak reflectance to the reflectance around 675 nm, which represents the red absorption peak of the chlorophyll-a [12]. For example, Gons et al. [13] first derived the backscattering coefficient at 704 nm and 672 nm, and then used the reflectance and absorption at these two wavelengths to predict the chlorophyll-a concentration; and Tiemann & Kaufman [14] used the ratio of 705 nm to 678 nm to estimate the chlorophyll-a concentration in the Mecklenburg Lake. More complex relationships have also been suggested. Gitelson et al. [15] developed the three-band model for MERIS spectral bands to estimate the chlorophyll-a concentration in turbid waters. Le et al. [12] used an improved algorithm of three-band and four-band models to assess the chlorophyll-a concentration in Taihu Lake.
The most widely applied models used for the chlorophyll-a concentration estimation assume that the optical parameters, such as the chlorophyll-a and the specific absorption coefficient, are constant. This assumption considerably impacts their accuracy [16-18], especially in the turbid water bodies like Taihu Lake. Additionally, most applied models are not suitable for multi-band remote sensors, such as the Landsat/TM, which prohibits their use with widely-available remote sensing resources. In this study, empirical models are introduced for the chlorophyll-a concentration retrieval based on the TM data for the turbid waters of Taihu Lake in China. The primary goal of this paper was to develop and validate these models and to determine their suitability for estimating the chlorophyll-a concentration distribution in Taihu Lake on October 27, 2003.
2. Materials and Methods
2.1. Data Acquisition
Located in east China, the Taihu Lake (Figure 1(a)) is a typical inland water body, influenced by river and human activity inputs with a low deposition rate. Because the water is highly turbid, the Taihu Lake was selected for this study. It was difficult to estimate the chlorophyll-a concentration of this lake accurately, as the optical properties of the water show great spatiotemporal variability [19]. The absorption signal of the chlorophyll-a from phytoplankton is partly overwhelmed by that of the suspended solids and backscattering. As a result, it is difficult to estimate the chlorophyll-a concentration accurately using conventional methods, such as the multiple bands and single band algorithms.
In situ measurements were carried out in the Taihu Lake on the 27th and 28th of October, 2003, which coincided with acquisition of Landsat-5/TM imagery for the lake. During the period of the satellite overpass (about ±1h) on October 27, 2003, the in situ measurements were carried out with the ASD field spectrometer at each station. Therefore, it is reasonable to assume that the in situ experiment on the ground was approximately synchronized with the satellite observation from space. The distribution of in situ sampling points is depicted in Figure 1(a) and the spectral curves of the in situ measurements are shown in Figure 1(b). The reflectance measurements were performed using a spectroradiometer with 25° fore-optic, covering the 350 nm-2500 nm spectral domain (Analytic Spectral Devices (ASD), Boulder, CO). The ASD had a spectral resolution of 3 nm (full-width-at-half-maximum, FWHM) and a 1.4nm sampling interval across the 350 nm-1050 nm spectral range [20]. The resulting data were interpolated by the ASD software during the collection to produce values at 1nm intervals. The experiments were conducted strictly in compliance with the Ocean Optical Protocols of NASA [21]. In order to compute the sub-surface irradiance reflectance, the radiance was measured from a calibrated reflectance panel before and after shading. Hyperspectral reflectance was calculated as follows [21]:
(1)
where 
is the water-leaving radiance, 
is the total incident radiant flux of the water surface, and 
is the remotely sensed reflectance. 
and 
in
(a)
(b)
Figure 1. The Taihu lake. (a) The location of the Taihu lake, with the blue flags representing the distributions of the in situ measurements; (b) in situ measurements of spectral curves corresponding to the sampling points in figure 1(a).
Equation (1) are further calculated as follows [12]:
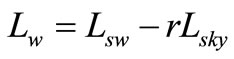(2)
(3)
where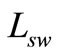 
denotes the total radiance received from the water surface; 
represents the diffused radiation of the sky, which contains no information on water properties, and hence has to be eliminated; r refers to the reflectance of the skylight at the air-water interface, whose value depends upon the solar azimuth, measurement geometry, wind speed, and surface roughness; 
is the radiance of the gray board; and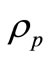 
is the reflectance of the gray board, which is accurately calibrated to 30%.
The limnological sampling was performed on the same day using a rosette sampler or bucket. After sampling, bottles with water samples were maintained at a low temperature and sent for laboratory analysis in the same day they were collected.
The in situ water sample measurements were divided randomly into two sets. One set was used to calculate the parameters of retrieving models, and included the dataset of 19 stations (called the “calibration data” below). The other set was used to validate the accuracy of the retrieving models, and included the dataset of 4 stations (called the “validation data” below).
2.2. Reflectance Calibration
Among the total signals received by the sensor at satellite altitudes, over 80% of that typically in blue spectral region was from the contribution of light scattering by molecules and aerosol particles in the atmosphere [22,23]. Thus, the water-leaving radiance, from which the phytoplankton concentration was derived, was only a portion of the total radiance arriving at the sensor. The process of retrieving the water-leaving radiance from the total radiance is usually referred to as the atmospheric correction. The general atmospheric correction algorithm was adopted to make an assessment of the corresponding band reflectance of imagery by using the special near-infrared spectral bands, whose reflectance is supposed to be zero in Morel’s Case I waters [22-24]. However, this standard atmospheric correction method is not applicable to the turbid water bodies, such as Taihu Lake, owing to the scattering at this wavelength by detrital material. Additionally, the near-infrared data from TM4 has been shown to exhibit an almost linear relationship with increasing quantities of suspended matter [17]. As a result, the atmospheric correction developed for clear water bodies by Gordon & Clark [24] is not applicable to the Case II water bodies [22,24].
In addition to the atmospheric effects, the adjacency effects are also highly significant in data acquired by the high spatial resolution sensors, such as the Landsat/TM [25]. Ouaidrari & Vermote [26] showed that the adjacency effects were strongly linearly related with the surface reflectance of imagery pixels. In order to eliminate the sensors sensitivity to atmospheric influences and adjacency effects, the water-leaving reflectance (
) from in situ measurements were used in this study to calibrate the reflectance (
) of the Landsat/TM imagery by Line Empirical Model for Reflectance Calibration (LEMRC) [27-29] as follows:
(4)
where 
is the wavelength,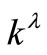 
is the attenuation coefficient corresponding to the wavelength
; 
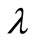is the atmospheric contributions to the reflectance; and 
and 
are considered as constants at a given wavelength and are approximated using the regression shown in Figure 2.
2.3. Constructions of Four Empirical Models
Various constituents of environmental water samples, such as the phytoplankton cells, detrital material, and colored dissolved organic matter (CDOM), affected the passage of light through the sample by scattering and absorption In general, the reflectance at lower wavelengths of 400-500 nm was relatively low due to the combined affects of absorption by the CDOM, tripton and phytoplankton pigments. A local maximum in reflectance around 550 nm-580 nm was caused by a local minimum in the combined effects of the low phytoplankton pigment absorption efficiency and lower CDOM and tripton absorption. A clear reflectance minimum was located at 676 nm, which corresponds to the in vivo chlorophyll-a maximum absorption peak. Beyond 680 nm, the reflectance increased significantly and reached a maximum at 706 nm [17]. This maximum could be used for interpretation of the signal due to the natural phytoplankton fluorescence [30], however, the Landsat/TM data did not have bands in this area.
The spectral absorption features, such as the height, area, and angle (Figure 3), have been widely used in the vegetation canopy remote sensing field studies. Shrestha et al. [31] used the absorption width, area and depth of reflectance curves for mapping land degradation. Walsh et al. [32] applied the Hyperion data and QuickBird data for the control and management of land use based on the analysis of those spectral characteristics due to an invasive plant species. This study explores the geometric triangle properties of multiple spectral remote sensing data to retrieve the chlorophyll-a concentration.
(a)
(b)
(c)
Figure 2. Relationships between the reflectance of TM imagery and in situ measurements at TM1, TM2 and TM3, respectively.
As shown in Figure 3, the lines AB, BC and AC denoting the vectors were as follows:
(5)
(6)
(7)
The area of triangle ABC, S, was calculated as follows:
(8)
The high of triangle ABC, h, was calculated as follows:
(9)
One angle of triangle ABC, α, was calculated as follows:
The spectral curves in Figure 1(b) show that the reflectance in the blue region (400-500 nm) was relatively low owing to high absorption by components of the water samples. The reflectances in the green region (500-600 nm) and red region (600-700 nm) were the primary and the secondary reflectance peaks, respectively, and result from the scattering of the suspended sediments and low absorption coefficients of both CDOM and chlorophyll-a pigment. Additionally, the reflectance in the blue region of the visible spectrum decreased at a rate nearly equivalent to that of the reflectance elevation in the green and red regions [33]. Due to the differential reflectance of the phytoplankton pigments at different wavelengths, the shape of the triangle as shown in Figure 3 would be deformed, resulting in the variance of the height, the area and the angle of the triangle. Accordingly, it was indicated that the geometrical quantities, such as the angle, height and area were strongly correlated with the reflectance at the three visible bands of the Landsat/TM image. According to these properties and a combination of Equation (8), Equation (9) and Equation (10), the geometrical quantities, such as the angle, height and area, were found to correlate excellently with the chlorophyll-a concentration.
3. Results and Discussion
3.1. Empirical Models
3.1.1. Model Calibration
To match the bandwidth of Landsat/TM, the ASD measurements were aggregated using the Landsat/TM sensor
(10)
Figure 3. The triangle properties between the three visible bands of Landsat; R1, R2 and R3 represent the remote sensing reflectance at TM1, TM2 and TM3; h represents the height of the triangle when the baseline is AC; α is the angle of < BAC.
spectral response functions before model calibration. The Landsat/TM sensor spectral response functions used in this study were suggested by Vries et al. [34]. All of these common empirical models were tested to determine the relationship between the chlorophyll-a concentration and the triangular geometric quantitative parameters. The geometrical variables of height and area were exponentially well correlated with the chlorophyll-a concentration in Taihu Lake (Figure 4). The regression coefficients of the HCCRM and ACCRM were 0.8023 and 0.7985, respectively. The regression coefficients of the HCCRM and ACCRM were higher than that of the RM, which was 0.3124. Interestingly, the relationship between the chlorophyll-a concentration and the geometrical variable of angle was not ideal. The correlation coefficient of the AgCCRM was only 0.001.
Figure 5 illustrates the relationship between the modeled prediction of HCCRM and ACCRM and the calibration data. Compared with the RM. both algorithms appeared perfectly suitable for estimating the chlorophyll-a concentration, though the ACCRM had a slightly superior performance compared with the HCCRM. Using HCCRM to estimate the chlorophyll-a concentration in Taihu Lake reduced the correlation coefficient of 0.0038 from HCCRM, and the Root Mean Square Error (RMSE) was decreased from 6.311 mg/L for ACCRM to 6.273 mg/L for HCCRM, while the mean measured value of the chlorophyll-a concentration of calibration data was 29.836 mg/L.
The relationship between the predicted chlorophyll-a concentration and the calibration data also revealed the ability of the two approaches in retrieving the chloro-
phyll-a concentration. Figure 5 shows a plot of predicted chlorophyll-a concentrations versus in situ measured
(a)ACCRM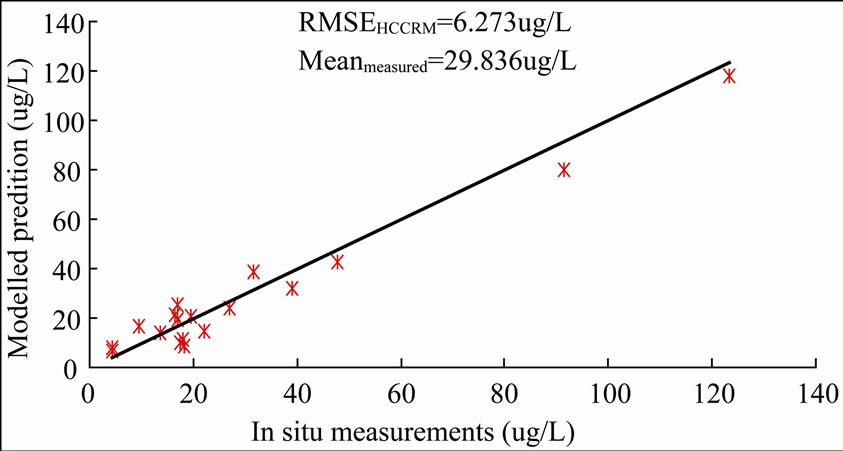
(b)HCCRM
Figure 5. Assessment of retrieval results. (a) presents the relationship between the chlorophyll-a concentration predictions of ACCRM and calibration data; (b) presents the relationship between the chlorophyll-a concentration predictions of HCCRM and calibration data.
values. Almost all points converged along the line of 
(where, 
denotes the in situ measured chlorophyll-a concentrations and 
denotes the chlorophyll-a concentrations predicted by the model). Despite minor differences in relative correlation coefficients and RMSE, the HCCRM and ACCRM were both suitable for chlorophyll-a concentration estimation in Taihu Lake. An additional operator of 
was included in the HCCRM and ACCRM. The coefficient value before term of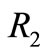 
equals the sum of the coefficients before the terms of 
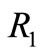and
, but the signs are opposite. This operator allows the model to eliminate some atmospheric influences, such as the linear effects on the bands of TM1, TM2, and TM3, which theoretically improves the accuracy of the retrieved results.
3.1.2. Model Validation
The performance of the HCCRM and ACCRM was evaluated by examining their respective RMSE in estimating the chlorophyll-a concentration. Figure 6 shows the relationship between the modeled prediction of HCCRM and ACCRM and the validation data. Both models produced accurate chlorophyll-a concentration predictions, but the performance of the HCCRM was slightly superior to that of the ACCRM. Compared with ACCRM, the uncertainty in estimating the chlorophyll-a concentration in Taihu Lake decreased by 2.39% with the use of the HCCRM, and the RMSE also decreased from 4.276 mg/L in ACCRM to 3.858 mg/L in HCCRM. The regression coefficient was 0.8023 in HCCRM and 0.7985 in ACCRM. The performances of HCCRM and ACCRM using the calibration data were consistent with those using the validation data. Additionally, the total errors between the modeled prediction and the validation data were used to estimate the total bias of the retrieved results. According to Figure 6, the total bias was –4.003 mg/L in ACCRM and –3.570 mg/L in HCCRM. Therefore, it was concluded that the HCCRM and ACCRM were both suitable for detecting and mapping the chlorophyll-a concentration in Taihu Lake on October 27, 2003, yet the HCCRM was slightly more accurate than the ACCRM.
3.2. Chlorophyll-A Mapping Based on TM Data
To estimate the water-leaving radiance from the total radiance measured at the sensor, the LEMRC (Figure 2) was used as the atmospheric correction algorithm to eliminate the atmospheric influence of TM1, TM2 and TM3 of Landsat images. Then the HCCRM and ACCRM were used to map the chlorophyll-a concentration in Taihu Lake.
Figure 7(a) and Figure 7(b) shows the chlorophyll-a maps of Taihu Lake on October 27, 2003 calculated from the HCCRM (Figure 4(a)) and ACCRM (Figure 4(b)), respectively. Overall, the chlorophyll-a concentrations throughout Taihu Lake, calculated by either HCCRM or ACCRM, were higher in the east, north and center of the lake but lower in the south of the lake (Figure 7). However, some significant differences could be found between the results from the two algorithms. The concentration range was 0-100 mg/L in HCCRM and 0-130 mg/L in ACCRM. The concentrations estimated by
Figure 6. Relationship between the modeled prediction of HCCRM and ACCRM and validation data.
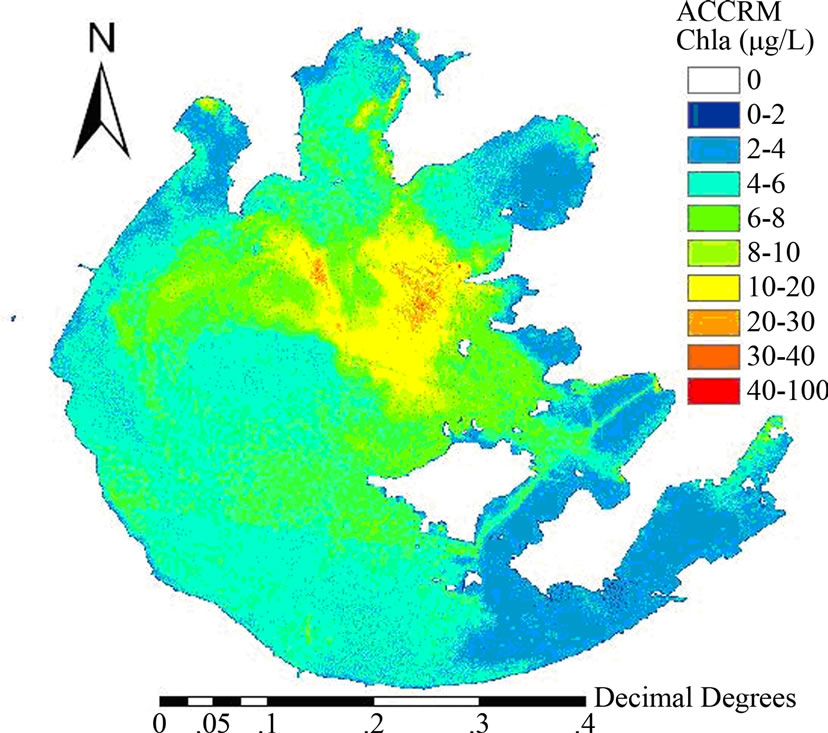(a) Chlorophyll-a map estimated by ACCRM
(b) Chlorophyll-a map estimated by HCCRM
Figure 7. Inversion results of the exponential empirical model of ACCRM and HCCRM as shown in Figure 3(a).
ACCRM were higher than those by HCCRM, especially at the prominent concentration range of 6-10 mg/L. The total biases of HCCRM and ACCRM given in Figure 6 reveal that the chlorophyll-a concentrations predicted by ACCRM were more underestimated than those by HCCRM.
4. Conclusions
Empirical algorithms are easy and straightforward for data processing. However, because the empirical coefficients contained in the empirical algorithms are derived from the data set they may not necessarily account for all natural variations. In this study, four experimental models for estimating the chlorophyll-a were constructed by specifying the remotely sensed parameters. They are the area, the height, the angle of a triangle and band ratio of TM2 to TM3. Using the calibration dataset, the evaluation of samples collected in Taihu Lake, China, on the 27th and the 28th of October, 2003, ACCRM and HCCRM showed better performance than the band ratio algorithms and AgCCRM. The HCCRM was slightly superior to the ACCRM based on the correlation coefficient and RMSE.
The performance of ACCRM and HCCRM was validated by the validation dataset. Both algorithms underestimated the chlorophyll-a concentration in Taihu Lake on October 27, 2003. The total bias was –4.003 mg/L in ACCRM and –3.570 mg/L in HCCRM, so the ACCRM underestimated more than the HCCRM. As a whole, both algorithms showed the spatial distribution of chlorophyll-a concentration was higher in the east, north and center of the lake, but was lower in the south of the lake. The concentration estimated by ACCRM was higher than that by HCCRM, especially at the prominent concentration range of 6-10 mg/L.
5. Acknowledgement
This study was supported by the National Key Technology R & D Program in the 11th Five Year Plan of China (2008BAC34B03) and the China National Great Geological Survey (GZH200900504).