1. Introduction
The Heisenberg group (of order
), 
is a noncommutative nilpotent Lie group whose underlying manifold is 
with coordinates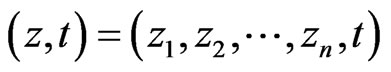 
and group law given by
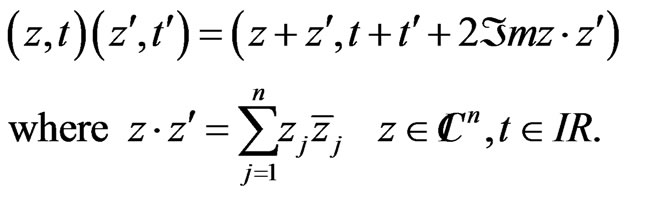
Setting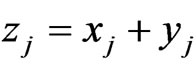
, then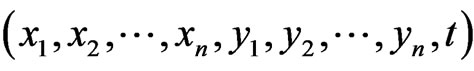 
forms a real coordinate system for
. In this coordinate system, we define the following vector fields:
The set 
forms basis for the left invariant vector fields on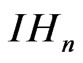 
[1]. These vector fields span the Lie algebra 
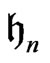of 
and the following commutation relations hold:
Similarly, we obtain the complex vector fields by setting
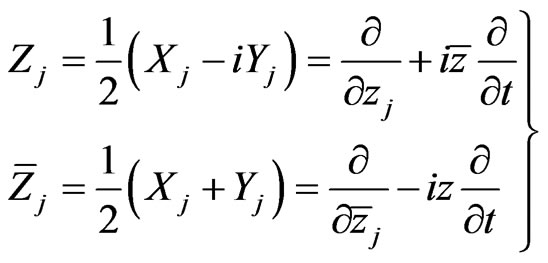
In the complex coordinate, we also have the commutation relations
If we identify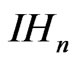 
with 
then each element of 
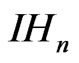is given by 
and the group law becomes
where 
denotes the scalar product of 
The neutral element 
of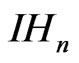 
is of the form 
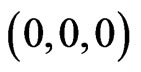and the inverse element
The centre of 
is given by
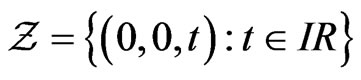
and therefore isomorphic to the additive locally compact topological group 
The Haar measure on 
is the Lebesgue measure 
on 
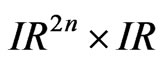[1].
On the group, we introduce the group 
of dilations defined for each element 
of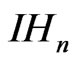 
by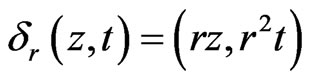 
on the complex coordinates and by 
on the real coordinates. The family of dilations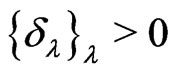 
forms a one-parameter group of automorphisms of 
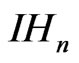Indeed, we have the following properties of this family of dilations.
(i) 
(ii)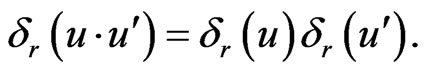 
Moreover(iii) 
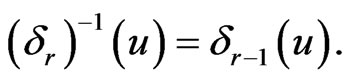Properties (i) and (iii) can be easily seen [2,3]. To see (ii), we notice that: For 
and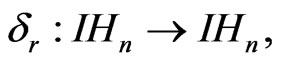 
we have
With these dilations as automorphisms of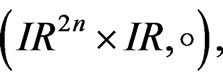 
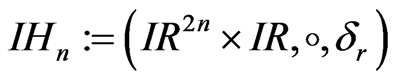becomes a stratified Lie group whose generators are the defined vector fields [4]. Similarly, 
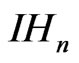and its Lie structure equipped with this family of dilations is a homogeneous group of dimension 
[5].
2. Homogeneous Norms on 
Definition 2.1: A norm on the Heisenberg group, is a function
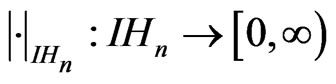(2.1)
satisfying the following properties:
(i)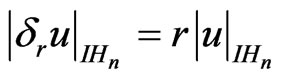
,
(ii)
,
(iii)
(iv) 
for all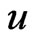 
and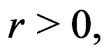 
where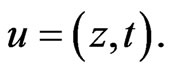 
The value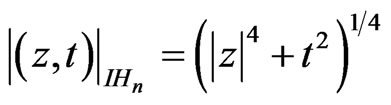 
is called the Heisenberg distance of 
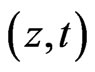from the origin and
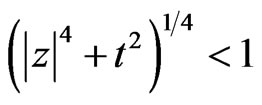is the Heisenberg unit ball [6]. We say the norm in 
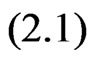is homogeneous of degree 
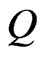with respect to the dilations if for any 
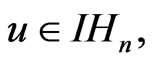we have
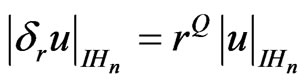. The value given by
is the popular Koranyi norm on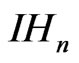 
which is always positive definite [7].
Property (i) is the homogeneity of the Heisenberg norm while property (iv) indicates the subadditivity of the Heisenberg norm. The proof of properties (i)-(iii) is trivial and that of (iv) can be found in [8].
Following [9], we shall further define the following norms on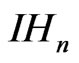
. For 
define
(2.2)
We notice that 
gives a choice which is not smooth away from the origin. The norm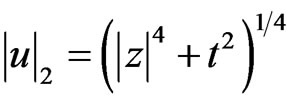 
and the properties above do not uniquely determine the norm. For if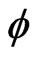 
is positive, smooth away from 0, and homogeneous of degree 0 in the Heisenberg group dilation structure, then 
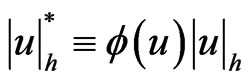gives another norm [10].
Since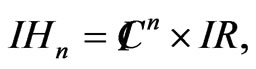 
it can be equipped with the Euclidean norm in 
denoted by 
and defined by
We have the following:
Proposition 2.3 [10]: For 
we have
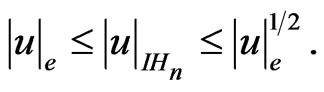
We notice however, that this norm is not homogeneous. In what follows, we show that homogeneous norms on the Heisenberg group are equivalent following [10].
Lemma 2.4: Let 
be a homogeneous norm on 
Then, there is a constant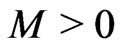 
such that
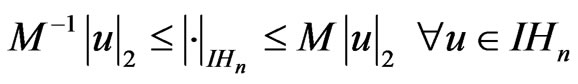
where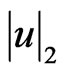 
is as defined in (2.2).
Proof: Now observe that 
is homogeneous of degree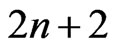 
and by hypothesis, 
is homogeneous. Let
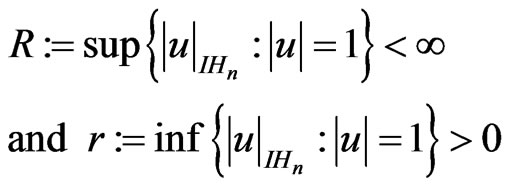
and set
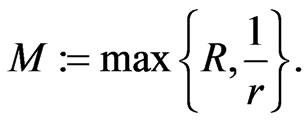
Now, if we identify 
as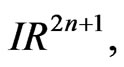 
then sup is actually a maximum and inf is a minimum. Thus 
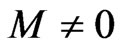exists and the inequality in the theorem holds. This is possible since 
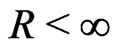and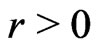 
follows from the fact that 
is a compact subset of 
not containing the origin and 
is a continuous function which is strictly positive in 
Corollary 2.5: For every fixed homogeneous norm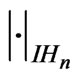 
on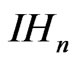 
there exists a constant 
such that
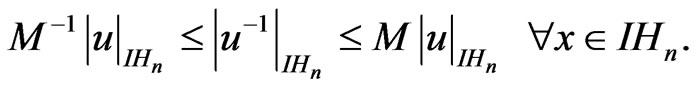
Proof: We notice that the norm function is continuous and therefore, 
Now consider the the group of dilations 
on 
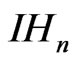Then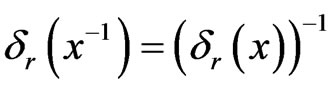 
is an automorphism of 
Therefore, by Lemma 2.4, the result follows.
Theory 2.6: Any two homogeneous norms on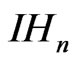 
are equivalent.
Proof: We apply the previous method as follows: Let
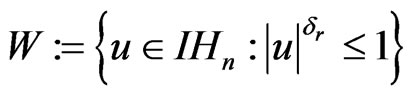
and define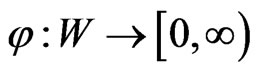 
by
Then
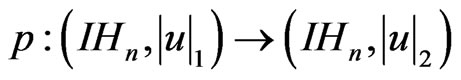
is obviously continuous by the homogeneity property with respect to 
Since 
is bounded with respect to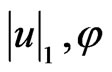 
attains it bounds and therefore, 
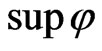exists. Thus, 
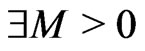such that 
If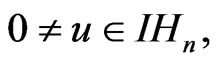 
then there exists 
such that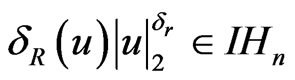 
so that
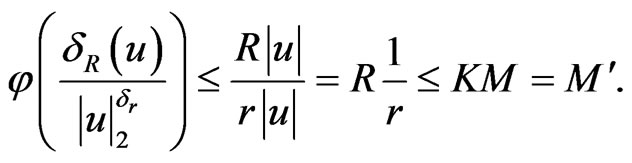
The theorem then follows by Lemma 2.4.