Effect of Rotation, Magnetic Field and Initial Stresses on Propagation of Plane Waves in Transversely Isotropic Dissipative Half Space ()
1. Introduction
In recent years, most of the researchers are interested to solve the problems related to electrically conducting elastic media permeated by uniform magnetic fields. The seismic wave propagation has been used for various studies related to magneto-elasticity on the Earth’s mantle and cores. By the knowledge related to reflection and refraction, the plane waves are the source of information used to image the Earth’s interior. Dissipation of the medium depends upon the internal structure. The initial stress in the medium may be developed due to some reasons such as slow process of creep, gravity, external forces, difference in temperature, etc.
Problem related to plane waves in transversely isotropic medium is very important for the possible application in various branches of science and technology such as earthquake science, acoustic, geophysics and optics etc. Biot [1] observed that the initial stresses have notable effect on the propagation on elastic waves in a medium. The problem related to reflection and refraction of elastic waves from the boundaries of different media has been discussed in the famous book by Achenbach [2]. Borejko [3] introduced the reflection and transmission coefficients for three dimensional plane waves in elastic media. By using the Biot’s theory [4] several researchers [5-9] have studied extensively the propagation of elastic waves. The problem related to reflection and refraction of qP and qSV waves at the interface of Fiber-reinforced medium has been discussed by Chattopadhyay and Venkateswarlu [10]. A huge amount of mathematical work has been performed for the propagation of elastic waves in dissipative medium; see for instance [11-14]. The problem related to thermo-magneto-dynamic stresses and perturbation of magnetic field vector in a non-homogeneous hollow cylinder has been studied by Kong et al. [15].
In the present study, we have used the Biot’s incremental deformation theory [4] for deriving the algebraic expressions of the reflection coefficients and energy ratios when plane waves of qP and qSV type are incident on the initially stressed dissipative half-space with stress free boundaries. The dispersion equations for reflection coefficients and energy ratios of incident qP and qSV waves on the free surface of the initially stressed dissipative medium have been derived and observed that in presence of initial stresses, magnetic field and rotation of the medium must affect the reflection coefficients and energy shares of reflected plane waves.
2. Formulation of the Problem
We consider the medium is a perfect electric conductor. The Maxwell’s equations of electromagnetic field for perfectly conducting elastic medium are given by Raychoudhuri and Banerjee [7].
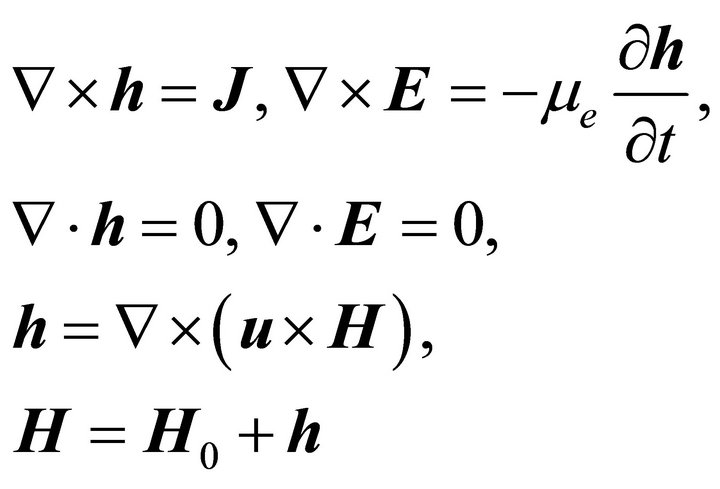 (1)
(1)
where,  is the Hamilton’s operator,
is the Hamilton’s operator, 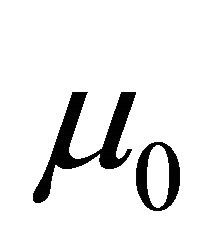 is the magnetic permeability,
is the magnetic permeability,  is the current density vector,
is the current density vector,  and
and 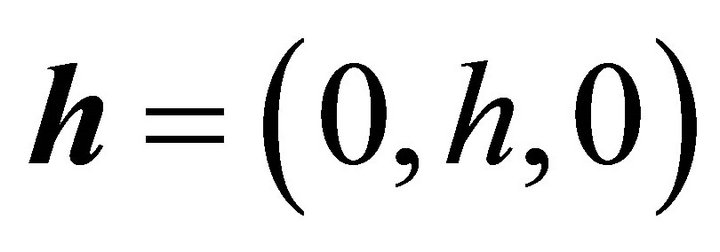 are the induced electric field and the induced magnetic field both are developed due to application of initial magnetic field
are the induced electric field and the induced magnetic field both are developed due to application of initial magnetic field 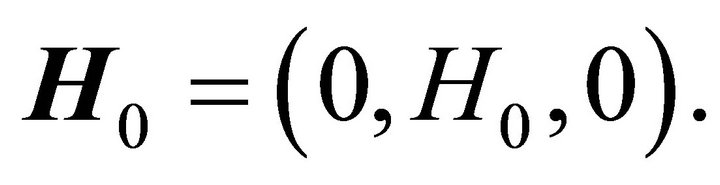
We consider a transversely isotropic dissipative half space rotating about y-axis 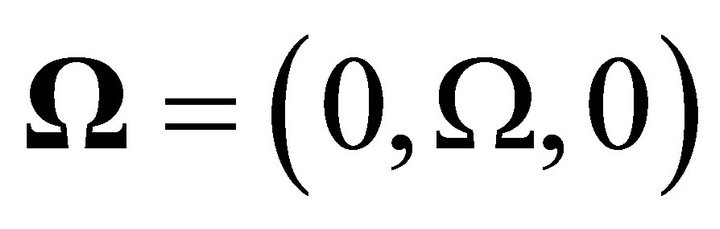 under constant magnetic field (along y-axis) and initial compressive stress P along x-axis (Figure 1).
under constant magnetic field (along y-axis) and initial compressive stress P along x-axis (Figure 1).
The equations of motion in x-z plane for the present problem may be written in the forms, given by Biot [1,4]
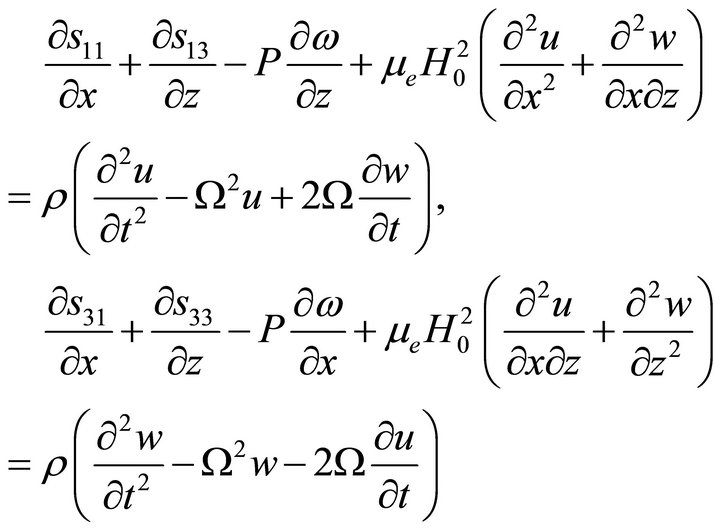 (2)
(2)
where  is density,
is density, 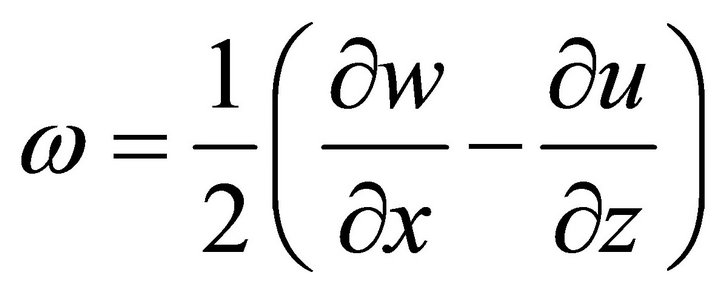 is the rotational component and
is the rotational component and 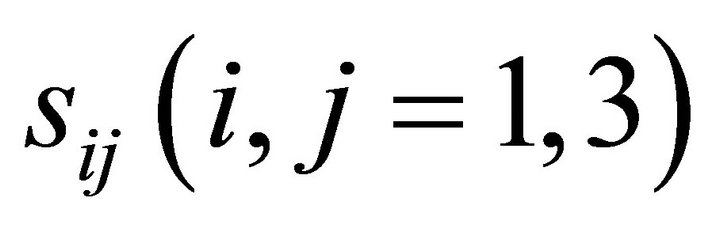 are incremental stress tensor in x-z plane.
are incremental stress tensor in x-z plane.
The stress-strain relation for transversely isotropic medium can be given by Biot [1]
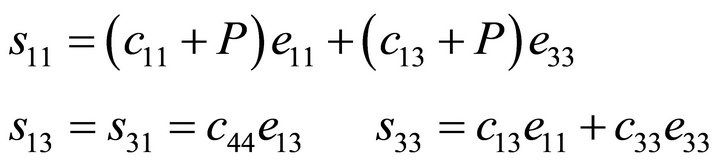 (3)
(3)
where 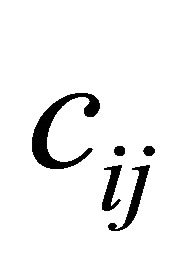 are the elastic coefficients.
are the elastic coefficients.
For dissipative medium, the elastic coefficients must be of complex constants, can be written as
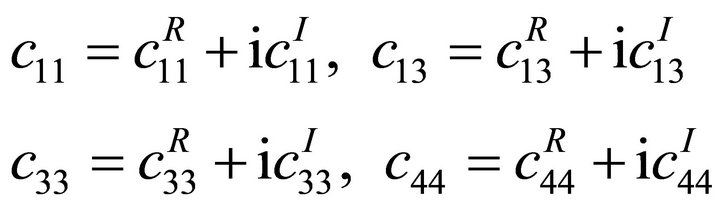 (4)
(4)
where 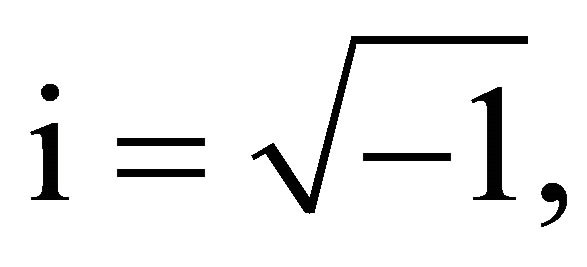
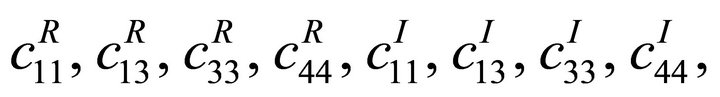 are all real constants.
are all real constants.
The incremental strain components 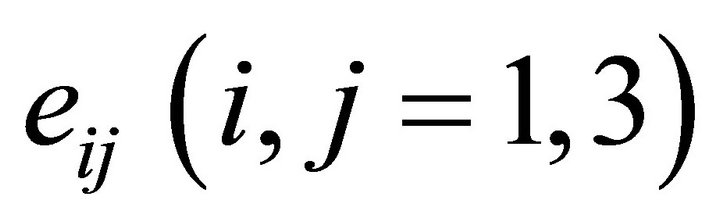 are related to the displacement components
are related to the displacement components  which are given by the relation
which are given by the relation
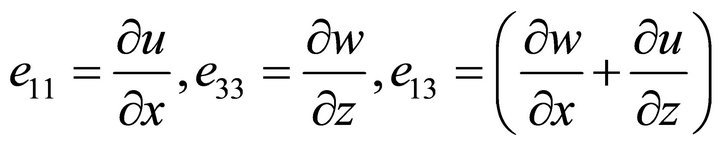 (5)
(5)
Let the harmonic solution of Equation (2), for the propagation of plane waves, the displacement components are written as follows:
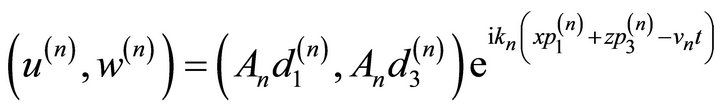 (6)
(6)
Where the index 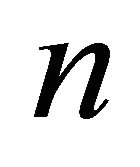 is assigns an arbitrary direction of propagation of the plane waves.
is assigns an arbitrary direction of propagation of the plane waves. 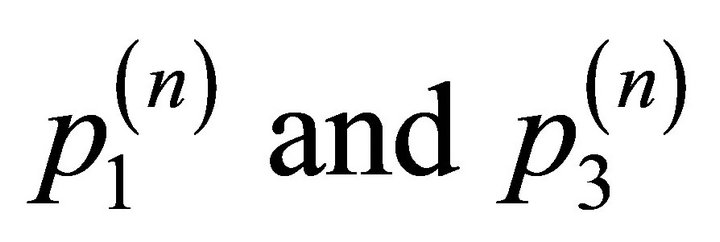 are cosine of angle made by direction of propagation with the normal (z-axis),
are cosine of angle made by direction of propagation with the normal (z-axis), 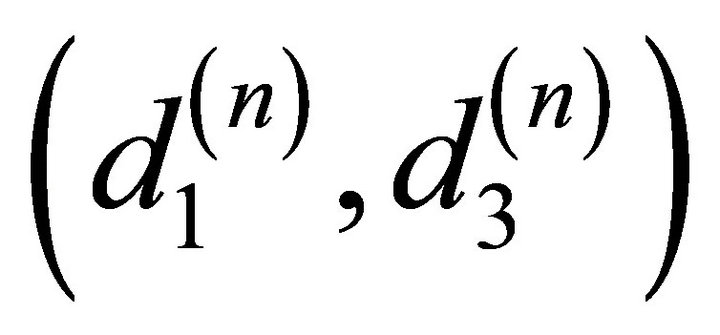 are the component of unit displacement vector,
are the component of unit displacement vector, 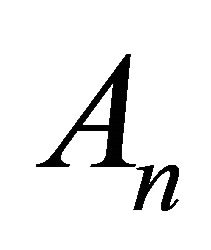 is the arbitrary constant and vn and kn are the velocity of propagation and corresponding wave number.
is the arbitrary constant and vn and kn are the velocity of propagation and corresponding wave number.
Substituting Equation (6) in (2) with the help of Equations (3)-(5) then we get the velocities correspond to quasi-P(qP) and quasi-SV(qSV) wave respectively.
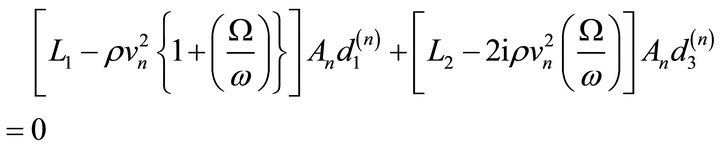 (7)
(7)
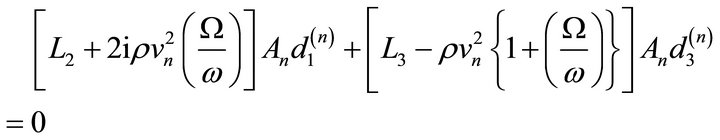 (8)
(8)
For non-trivial solution of Equations (7) and (8), the determinant must be equal to zero. That gives two values of 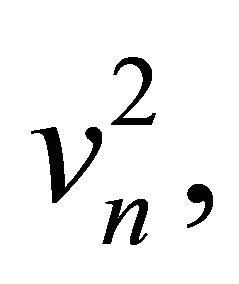 which are given by
which are given by
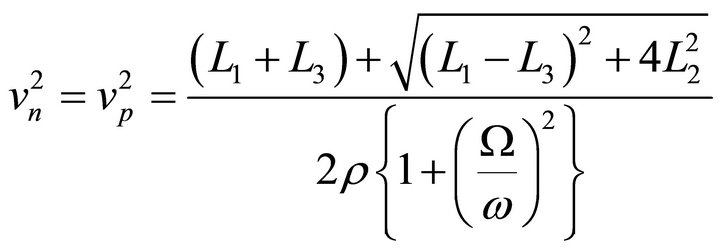 (9)
(9)
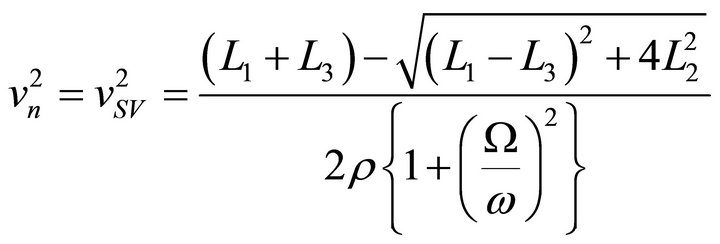 (10)
(10)
where
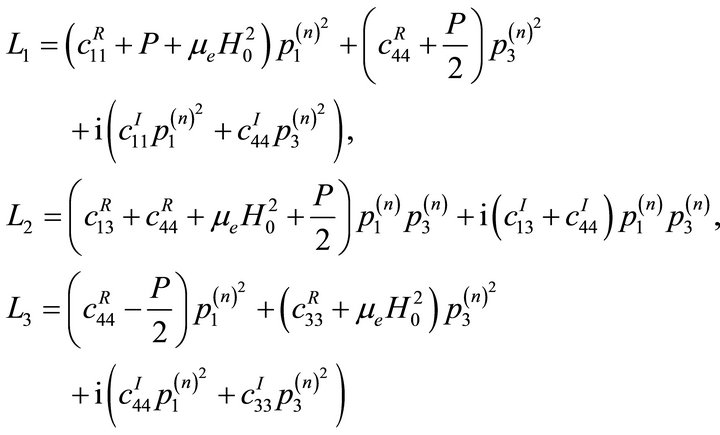
The real and imaginary parts of Equations (9) and (10) represents the phase velocities and damping velocities of qP and qSV waves, respectively. From the Equations (9) and (10), we can say that both vP and vSV depend on initial stresses, rotation, magnetic field, damping and direction of propagation 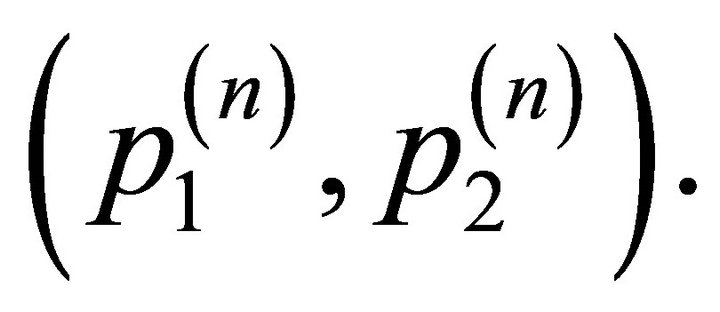 Also relation between the unit displacement vectors can be given as
Also relation between the unit displacement vectors can be given as
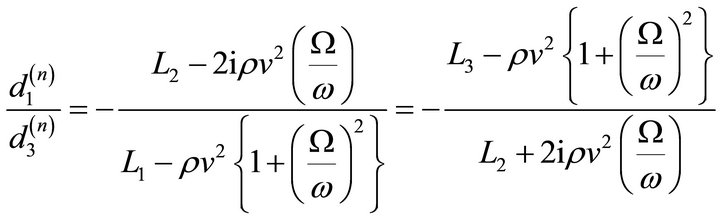 . (11)
. (11)
3. Reflection of Plane Waves from Stress Free Surface
We consider an initially stressed rotating magneto-elastic transversely isotropic dissipative half space absorbing the region 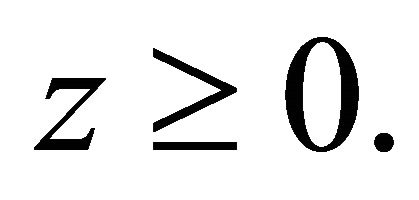 In this section, we are discussing about the reflection coefficients for incident qP and qSV waves.
In this section, we are discussing about the reflection coefficients for incident qP and qSV waves.
The displacement components of solid particles in transversely isotropic dissipative medium due to presence of an incidence wave and reflected waves are expressed as follows:
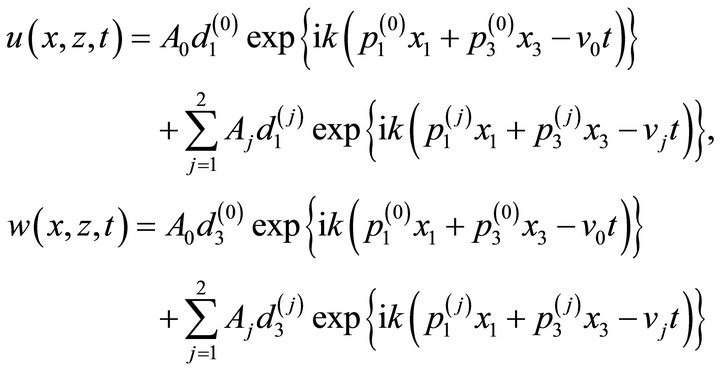 (12)
(12)
We are assuming the superscript 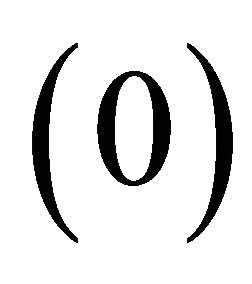 for incident qP and qSV waves, (1) for reflected qP waves and (2) for reflected qSV waves.
for incident qP and qSV waves, (1) for reflected qP waves and (2) for reflected qSV waves.
The boundary conditions for the free surfaces are vanishing of incremental boundary forces. So, the two boundary conditions required to be satisfied at the plane 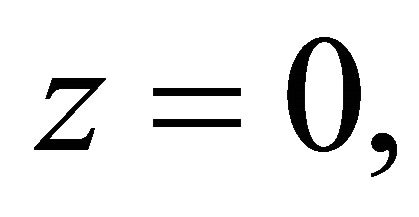 are
are
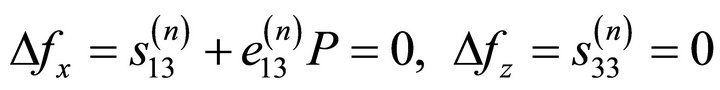 (13)
(13)
Equation (13) can be written as
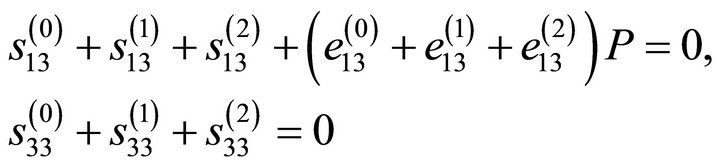 (14)
(14)
Equation (12) will satisfy the boundary conditions (14), if the following Snell’s law holds
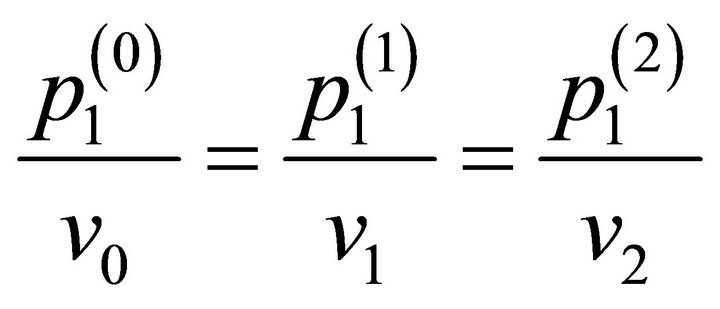 (15)
(15)
with the relations
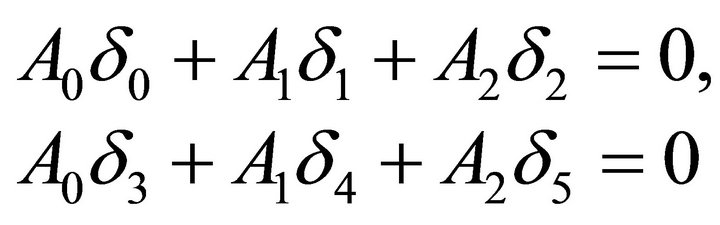 (16)
(16)
where
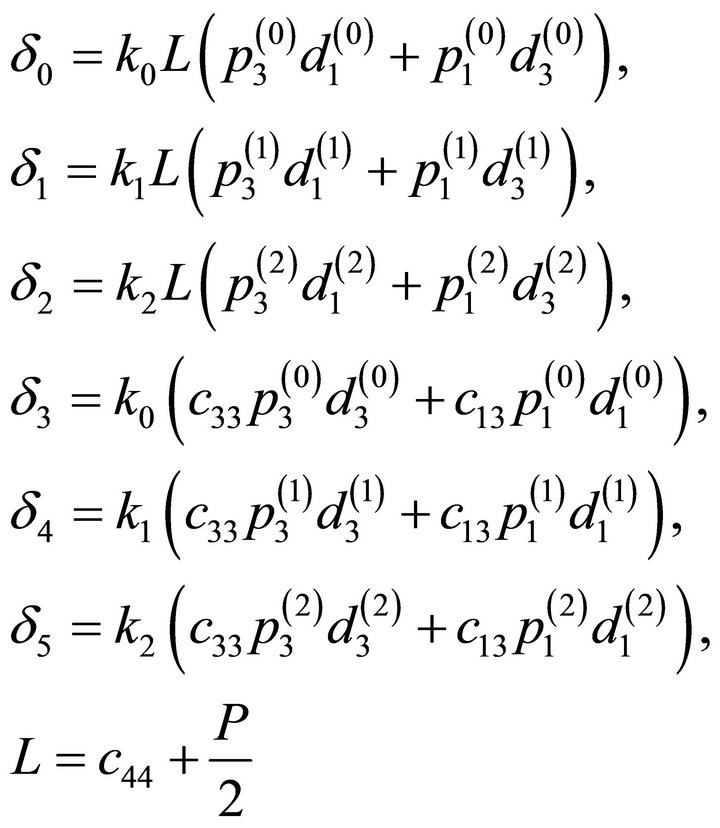 (17)
(17)
The amplitude ratios for incidence qP and qSV waves can be given by
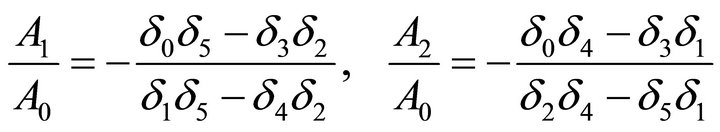 (18)
(18)
The real part of Equation (18) allow to determine the reflection coefficients of the reflected qP and qSV waves at a given incident qP and qSV waves. The reflection coefficients are denoted by ZPP (the incident qP wave is reflected as the qP wave), ZPS (the incident qP wave is reflected as the qSV wave), ZSP (the incident qSV wave is reflected as the qP wave) and ZSS (the incident qSV wave is reflected as the qSV wave).
4. Energy Ratios
We are considering the surface element of unit area at the half space  Our main purpose is to calculate the distribution of energy (of the incident wave) among the two reflected waves on this half space. Following Achenbach [2], the rate at which the incident energy transmitted per unit area is given by the scalar product of surface traction and particle velocity denoted by
Our main purpose is to calculate the distribution of energy (of the incident wave) among the two reflected waves on this half space. Following Achenbach [2], the rate at which the incident energy transmitted per unit area is given by the scalar product of surface traction and particle velocity denoted by 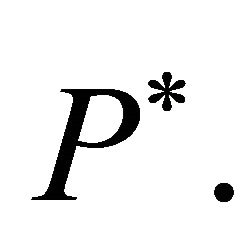 The time average of
The time average of 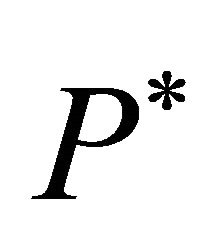 over a period, denoted by
over a period, denoted by 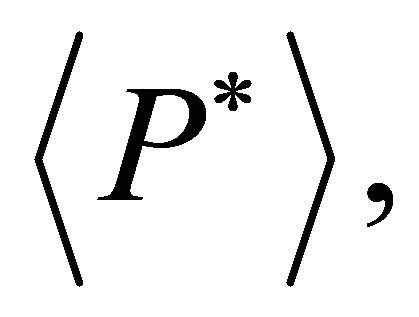 represents the average energy transmission per unit area per unit time.
represents the average energy transmission per unit area per unit time.
The average energy flux, for a given surface with normal along z-direction is represented through the components 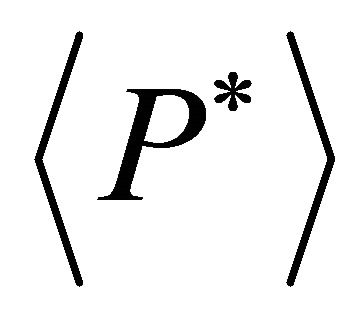 is given by
is given by
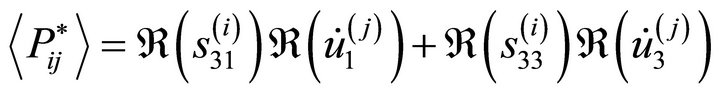 (19)
(19)
The distribution of incident energy is given in the form of a matrix at the free surface of the dissipative medium.
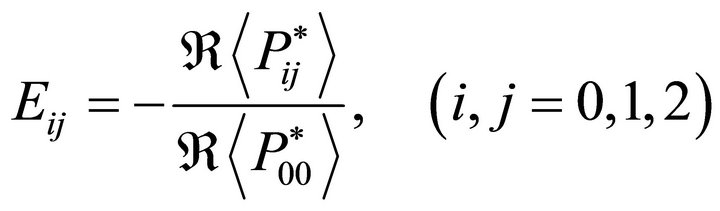 (20)
(20)
The element of matrix  is defined as follows:
is defined as follows:
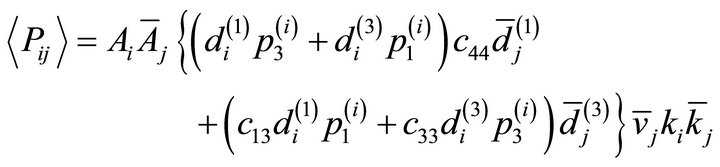 (21)
(21)
where bar over entity implies complex conjugate. The sum of all non-diagonal entries of this matrix calculates the share of interaction energy in the medium. The diagonal entries E11 and E22 of the matrix (Equation (20)) denote the energy shares of reflected qP and qSV waves in the incident energy. The energy due to interaction between incident wave and two reflected waves is given by
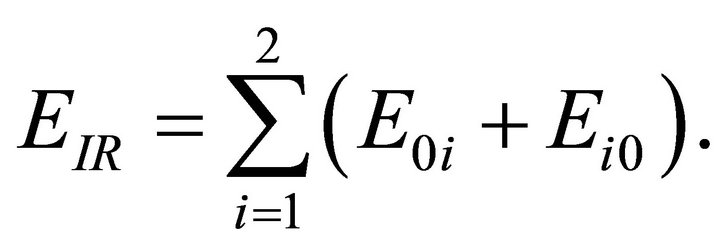 The energy due to the interaction among the two reflected waves is given by
The energy due to the interaction among the two reflected waves is given by
 The conservation of the energy at the free-surface is given by the relation.
The conservation of the energy at the free-surface is given by the relation.
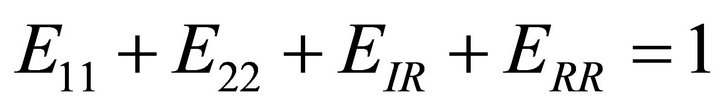 (22)
(22)
5. Numerical Results and Discussion
Material parameter for copper-alloy is chosen for the numerical model of magneto-elastic medium. The elastic and dynamic constants are given by [8,11]
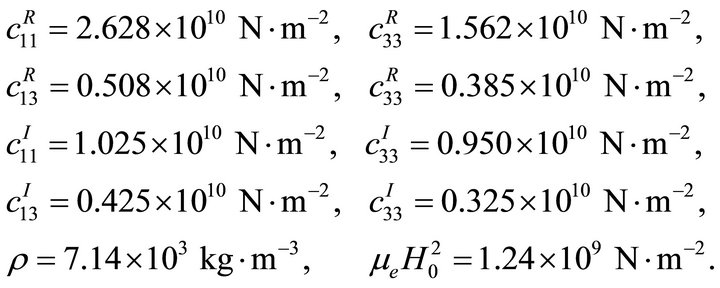
The given values of various parameters are used to calculate the complex velocities (qP and qSV waves) reflection coefficients (ZPP, ZPS, ZSP and ZSS) and energy shares (E11, E22, EIR and ERR) in the dissipative medium. The variation of reflection coefficients and Energy ratios with angle of incidence (θ) are shown in Figures 2-5 (for incidence qP wave) and in Figures 6-9 (for incidence qSV wave).
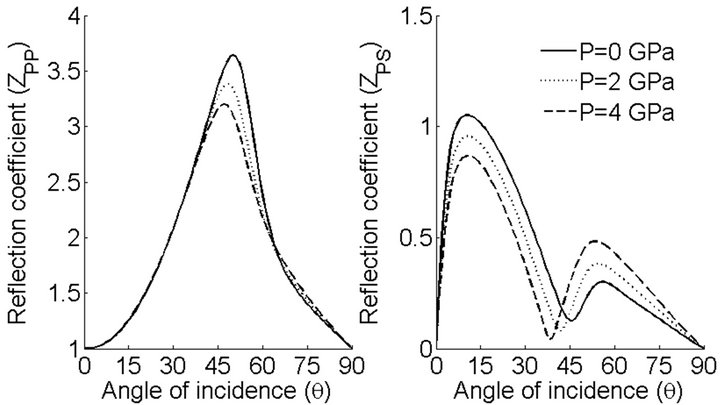
Figure 2. Reflection coefficients of qP and qSV waves with variations in incident angle (θ) and initial stress P for incident qP wave.
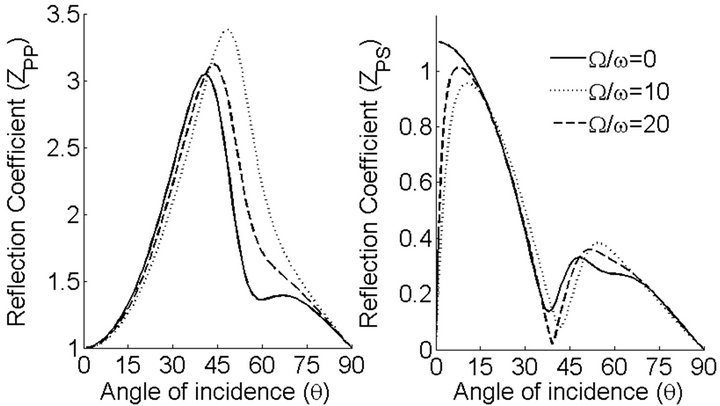
Figure 3. Reflection coefficients of qP and qSV waves with variations in incident angle (θ) and Effect of rotation parameter 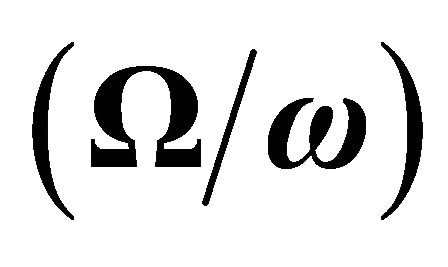 for incident qP wave.
for incident qP wave.
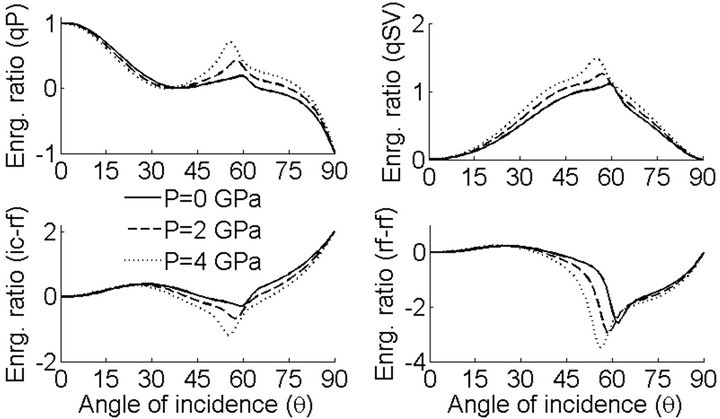
Figure 4. Energy shares of reflected (qP, qSV) waves, incident and reflected waves interaction and interaction among reflected waves, variations with incident angle (θ) and Initial stress (P) for incident qP wave.
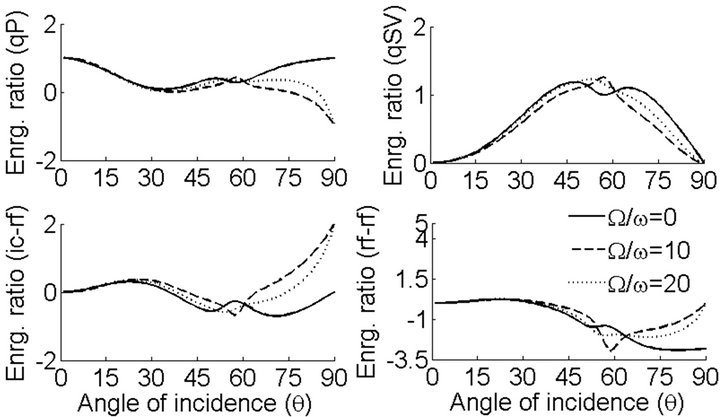
Figure 5. Energy shares of reflected (qP, qSV) waves, incident and reflected waves interaction and interaction among reflected waves, variations with incident angle (θ) and rotational parameter 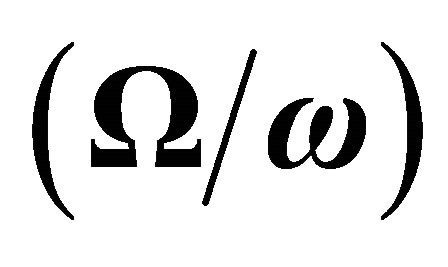 for incident qP wave.
for incident qP wave.
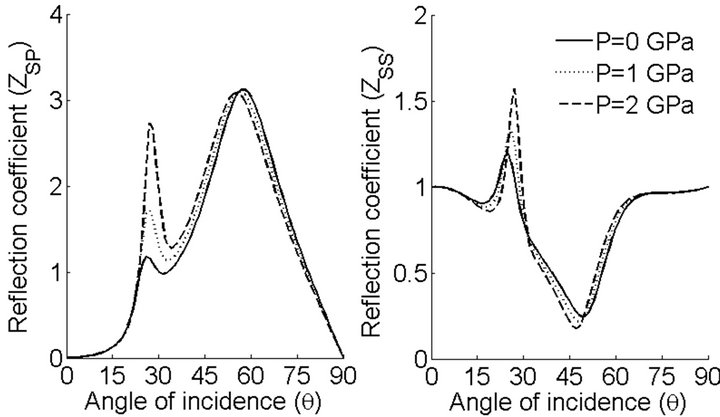
Figure 6. Reflection coefficients of qP and qSV waves with variations in incident angle (θ) and initial stress (P) for incident qSV wave.
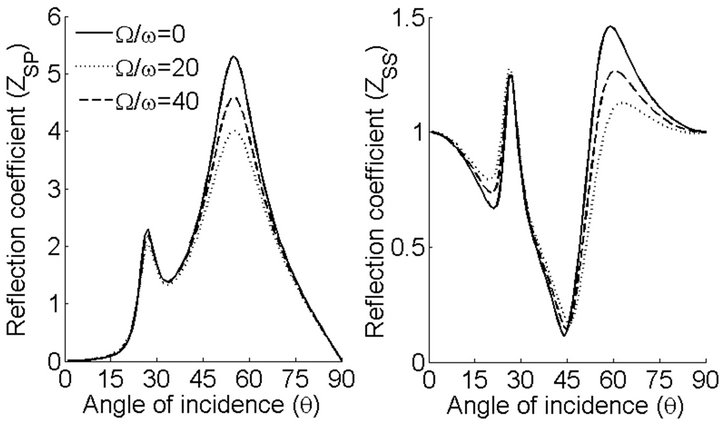
Figure 7. Reflection coefficients of qP and qSV waves with variations in incident angle (θ) and Effect of rotation parameter 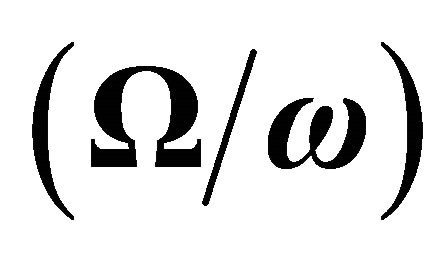 for incident qSV wave.
for incident qSV wave.
Figure 2 shows that the variation in the reflection coefficients (ZPP and ZPS) with respect to angle of incidence (θ) for different values of initial stress (P). The comparison of the solid and dashes lines shows that the reflection coefficients ZPP and ZPS change in presence of initial stresses for each angle of incidence of qP wave except grazing incidence. The effect of initial stresses is mini-