1. Introduction
All graphs in this paper are simple and denoted by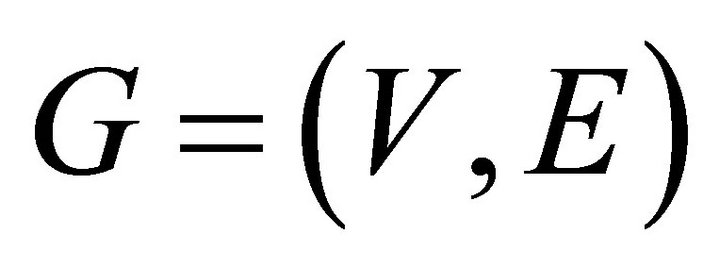 . The
. The  -edge coloring of a graph is an assignment of
-edge coloring of a graph is an assignment of  colors to the edges of the graph so that adjacent edges have different colors. The minimum required number of colors for the edges of a given graph is called the edge chromatic number of the graph and it is denoted by
colors to the edges of the graph so that adjacent edges have different colors. The minimum required number of colors for the edges of a given graph is called the edge chromatic number of the graph and it is denoted by . In the next section, we compute some extremal overfull graphs and finally, in section three, we determinethe class of plannar overfull graph. Throughout this paper, our notation is standard and mainly taken from [1].
. In the next section, we compute some extremal overfull graphs and finally, in section three, we determinethe class of plannar overfull graph. Throughout this paper, our notation is standard and mainly taken from [1].
2. Results and Discussion
Let  be the maximum degree of vertices of graph
be the maximum degree of vertices of graph . Obviously,
. Obviously, 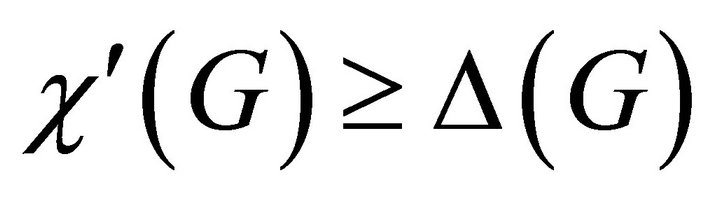 , and by Vizing’s theorem
, and by Vizing’s theorem . In other words,
. In other words, 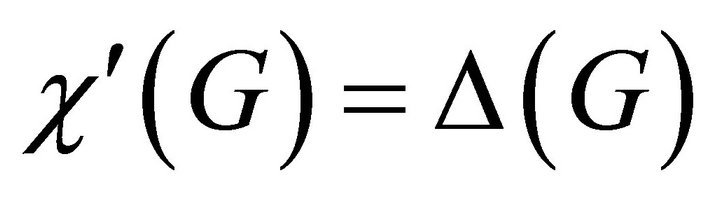 or
or . The graph
. The graph  is said to be of class 1 whenever,
is said to be of class 1 whenever,  and otherwise, it is said to be of class 2.
and otherwise, it is said to be of class 2.
Let  be a graph with
be a graph with  vertices and
vertices and  edges, then
edges, then  is overfull graph if
is overfull graph if . It is easy to see that the number of vertices of an overfull graph is an odd number and they are class 2. The following lemma, directly can be derived from the definition:
. It is easy to see that the number of vertices of an overfull graph is an odd number and they are class 2. The following lemma, directly can be derived from the definition:
Lemma 1. Every 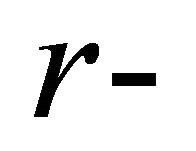 regular graph is overfull, where
regular graph is overfull, where  is an even and
is an even and  is an odd integers.
is an odd integers.
The concept of overfull graph play a significant role in understanding of the edge chromatic properties of graphs. Chetwynd and Hilton [2] conjectured that a vaste category of graphs are class 2 if they contain an overfull subgraph with the same maximum degree:
Conjecture (Overfull Conjecture). A graph  with
with 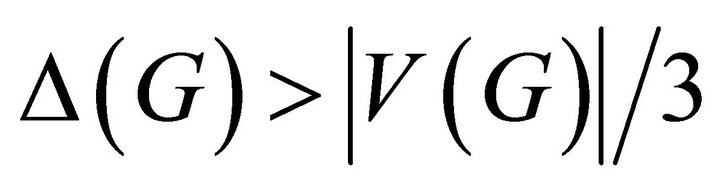 is class 2 if and only if it contains an overfull subgraph
is class 2 if and only if it contains an overfull subgraph  such that
such that .
.
We know that this conjecture is solved under special conditions (see e.g. [3,4]).
The aim of this section is to compute the maximal and minimal overfull graphs. We show that trees and unicycle graphs are not overfull. In continuing, we compute the second, the third and the fourth extremal overfull graphs. Throughout this section suppose  is a graph with
is a graph with 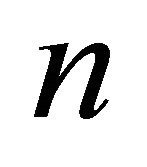 vertices and
vertices and  edges, where
edges, where  is an odd integer. Let
is an odd integer. Let  be an edge of
be an edge of  and
and 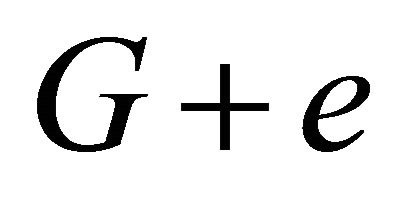 be a graph obtained from
be a graph obtained from  by adding
by adding . If
. If  be again an overfull graph, then
be again an overfull graph, then  is not a pendant edge, since the number of vertices of an overfull graph is an integer. Further, we have the following lemma:
is not a pendant edge, since the number of vertices of an overfull graph is an integer. Further, we have the following lemma:
Lemma 2. Let  be a connected graph with an odd
be a connected graph with an odd  vertices. If
vertices. If  has a pendent edge, then
has a pendent edge, then  is not overfull.
is not overfull.
Proof. Suppose  has a pendent vertex and
has a pendent vertex and . So, the maximum number of edges is
. So, the maximum number of edges is

So,  is not overfull. Similarly, one can see that in other cases
is not overfull. Similarly, one can see that in other cases  is not overfull.
is not overfull.
Lemma 3. If  be a unicycle overfull graph, then
be a unicycle overfull graph, then  is a cycle.
is a cycle.
Proof. Let  be a unicycle overfull graph, thus
be a unicycle overfull graph, thus  and so
and so . Since
. Since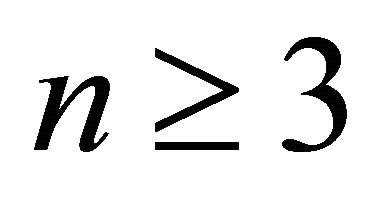 , hence
, hence  and then
and then .
.
• If  then
then  if and only if
if and only if , a contradiction.
, a contradiction.
• If  then
then  and the proof is completed.
and the proof is completed.
An overfull graph is minimal if it has the minimum number of edges among all  vertices overfull graphs and it is maximal if it has the maximum number of edges. In the following theorem we find the minimal and maximal overfull graphs:
vertices overfull graphs and it is maximal if it has the maximum number of edges. In the following theorem we find the minimal and maximal overfull graphs:
Theorem 1. Let , then among all
, then among all 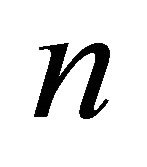 vertices overfull graphs, the complete graph
vertices overfull graphs, the complete graph  is maximal and the cycle
is maximal and the cycle  is minimal.
is minimal.
Proof. Let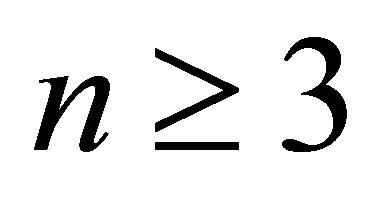 , the first claim is clear. For the second, since
, the first claim is clear. For the second, since  is overfull then
is overfull then  and so,
and so, . This implies that
. This implies that  has a cycle. Clearly,
has a cycle. Clearly,  is minimal overfull graph if and only if
is minimal overfull graph if and only if . By using Lemma 3,
. By using Lemma 3,  and so
and so  is a cycle.
is a cycle.
In Lemma 3, we classified the unicycle graphs on  edges. In continuing, let
edges. In continuing, let 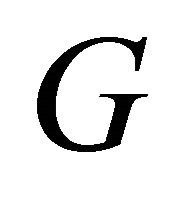 be a graph with
be a graph with  edges, since
edges, since  is overfull, thus
is overfull, thus

But  implies that
implies that  and hence
and hence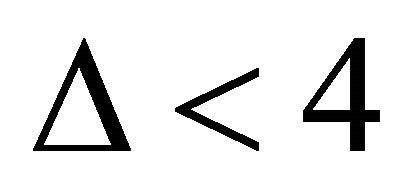 .
.
• If  then
then  is a graph on
is a graph on  vertices with
vertices with  edges, a contradiction.
edges, a contradiction.
• If  then
then 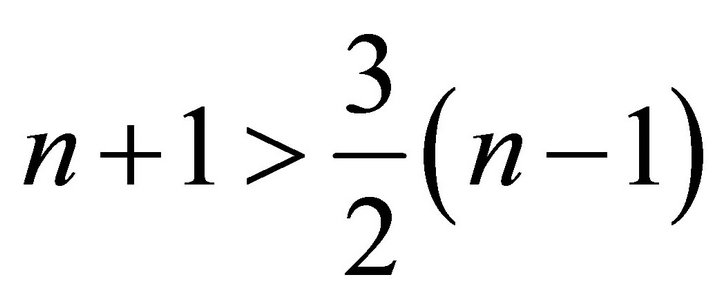 if and only if
if and only if , a contradiction.
, a contradiction.
Therefore we proved the following theorem:
Theorem 2. Let  be a graph on
be a graph on  vertices and
vertices and  edges, then
edges, then  is not overfull.
is not overfull.
As a result of the last theorem one can see that the second minimal overfull graph is not belong to the class of  graphs.
graphs.
Let  be an arbitrary edge of a cycle
be an arbitrary edge of a cycle  on
on 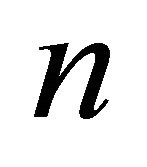
vertices. Add  new edges to
new edges to , parallel with
, parallel with 
and then join an endpoint of  to the remained vertex of degree 2, the resulted graph is an overfull graph and we denote it by
to the remained vertex of degree 2, the resulted graph is an overfull graph and we denote it by .
.
Here, we determine the second extremal overfull graph. Let us consider graphs with 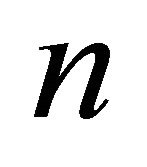 vertices and
vertices and  edges. It is easy to see that
edges. It is easy to see that

Since , so
, so  and we have the following cases:
and we have the following cases:
• If , then
, then  if and only if
if and only if 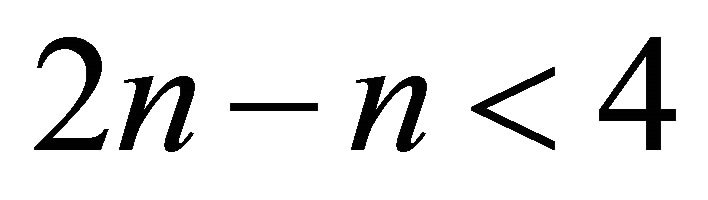 if and only if
if and only if , a contradiction.
, a contradiction.
• If , then
, then  if and only if
if and only if , if and only if
, if and only if . Clearly,
. Clearly,  and in this case,
and in this case,  is overfull graph isomorphic with
is overfull graph isomorphic with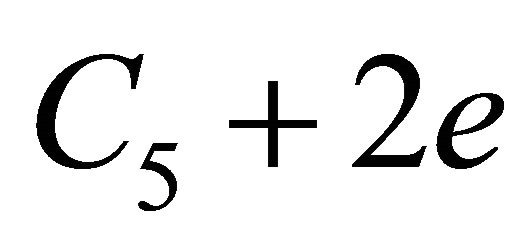 . So, we proved the following theorem:
. So, we proved the following theorem:
Theorem 3. Among all graphs on  vertices and
vertices and  edges, only
edges, only  is overfull.
is overfull.
Let now 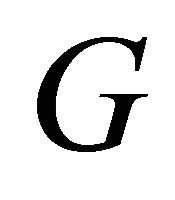 be a graph with
be a graph with  vertices and
vertices and 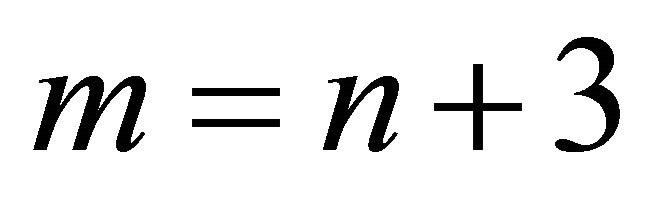 edges. By a similar way with Theorem 2, one can see that
edges. By a similar way with Theorem 2, one can see that  if and only if
if and only if .
.
Since 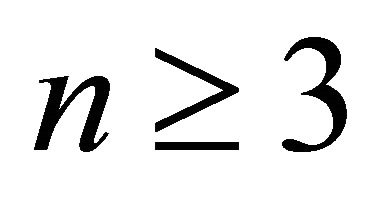 thus
thus 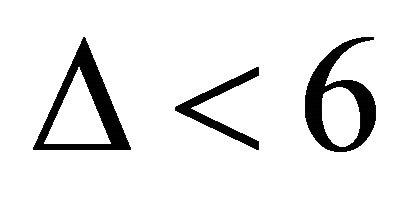 and so we have three following cases:
and so we have three following cases:
• If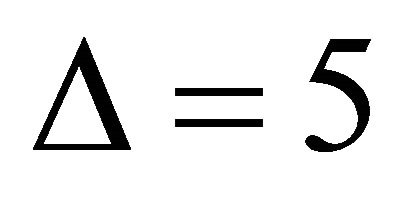 , then
, then , a contradiction• If
, a contradiction• If , then
, then , a contradiction• If
, a contradiction• If , then
, then , therefore
, therefore  or
or .
.
In the case , we must have a graph with five vertices, eight edges and
, we must have a graph with five vertices, eight edges and  which is impossible. If
which is impossible. If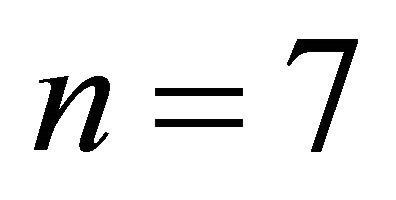 , then
, then 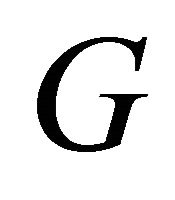 is overfull and it is isomorphic with
is overfull and it is isomorphic with  and soTheorem 4. Among all graphs on
and soTheorem 4. Among all graphs on 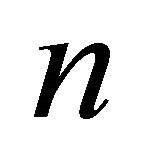 vertices and
vertices and  edges, only
edges, only  is overfull.
is overfull.
In the following theorem the second extremal overfull graphs are computed:
Theorem 5. Let  be an integer, then
be an integer, then
• The second maximal overfull graph on  vertices is
vertices is • The second minimal overfull graph on
• The second minimal overfull graph on  vertices is
vertices is .
.
Proof. By using Theorem 1, the proof of the first claim is clear. For the second part, note that 
has a vertex of degree 2 and the others have degree 3. So, by Euiler Theorem, we have:
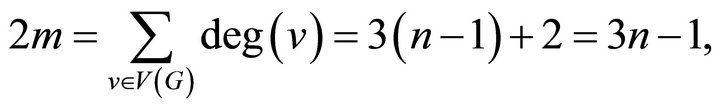
thus,
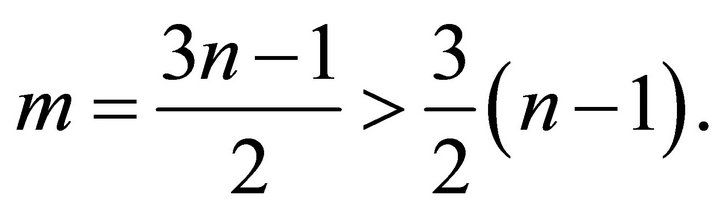
This implies that 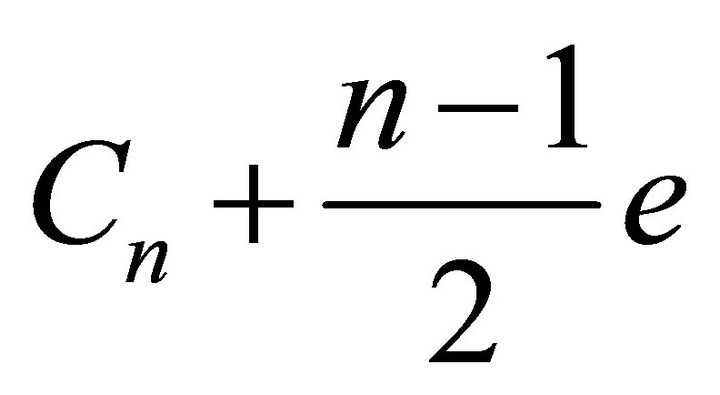 is overfull. On the other hand,
is overfull. On the other hand, . This means that
. This means that  has the minimum possible edges by this properties and this completes the proof.
has the minimum possible edges by this properties and this completes the proof.
To find the the third minimal overfull graph, note that the second minimal has  vertices of degree 3, so by adding a new edge to it we have
vertices of degree 3, so by adding a new edge to it we have  and so:
and so:
Theorem 6. Let  be an integer, then
be an integer, then
• The third maximal overfull graph on five vertices is isomorphic with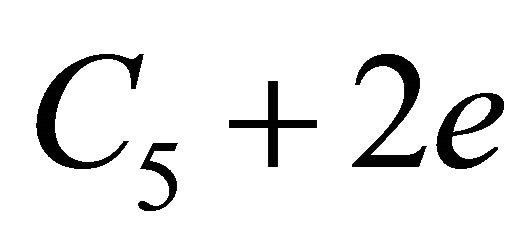 .
.
• If  then, the third maximal overfull graph on
then, the third maximal overfull graph on  vertices is
vertices is • The third minimal overfull graph with
• The third minimal overfull graph with  vertices is a graph constructed by removing an edge from a 4-regular graph.
vertices is a graph constructed by removing an edge from a 4-regular graph.
Proof. The proofs of the first and second claims are trivial. For a minimal graph satisfies in the third condition, it is neccesary that  and so,
and so,
 . On the other hand, if
. On the other hand, if  be the number of vertices of degrees 3 and 4, respectively, then
be the number of vertices of degrees 3 and 4, respectively, then  and
and . By solving these equations we find that
. By solving these equations we find that  and
and . So, the third minimal graph has exactly two vertices of degree 3 and the others are degree 4. It means that we can remove an edge from a 4-regular graph to obtain the third minimal.
. So, the third minimal graph has exactly two vertices of degree 3 and the others are degree 4. It means that we can remove an edge from a 4-regular graph to obtain the third minimal.
Corollary 1. By the conditions of last theorem:
• The fourth maximal overfull graph on five vertices is isomorphic with • For
• For  the fourth maximal overfull graph is isomorphic with
the fourth maximal overfull graph is isomorphic with • The fourth minimal overfull graph is a 4-regular graph on
• The fourth minimal overfull graph is a 4-regular graph on  vertices.
vertices.
3. Plannar Overfull Graphs
In this section, we classify all plannar overfull graphs. To do this, we need followin lemma:
Lemma 4 [1]. If  be a plannar graph on
be a plannar graph on  vertices and
vertices and  edges, then
edges, then .
.
Theorem 7. Let  be a plannar overfull graph, then
be a plannar overfull graph, then
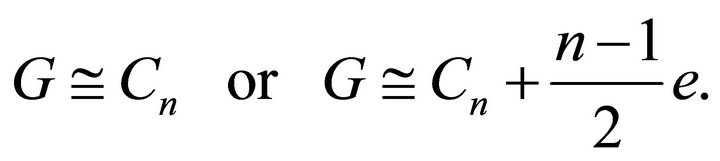
Proof. Since  is plannar overfull graph, then
is plannar overfull graph, then

This implies that . Because
. Because , hence
, hence  and we have the following cases:
and we have the following cases:
• If , then
, then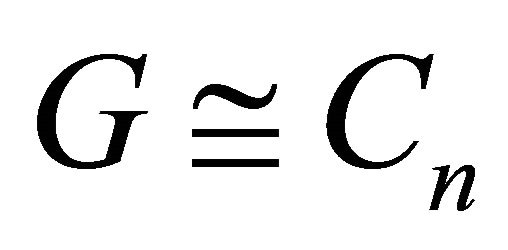 • If
• If , then by Lemma 2,
, then by Lemma 2,  has no a pendant vertex. Let
has no a pendant vertex. Let  be the number of vertices of degrees 2 and 3, respectively. Thus,
be the number of vertices of degrees 2 and 3, respectively. Thus,  and
and . Hence,
. Hence, 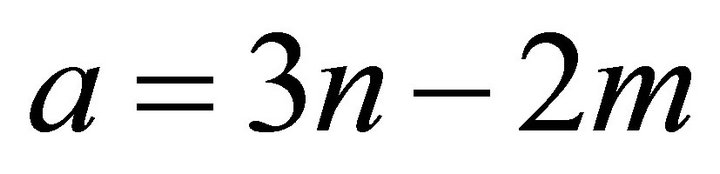 and
and . Since
. Since  and
and  is overfull graph, then
is overfull graph, then
 and so
and so . Clearly,
. Clearly, 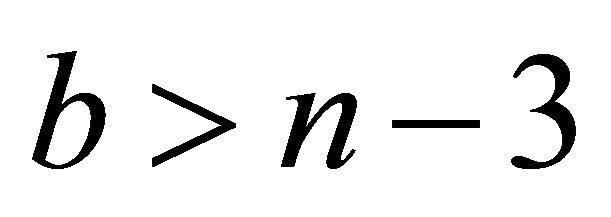 and we have the following cases:
and we have the following cases:
Case 1. 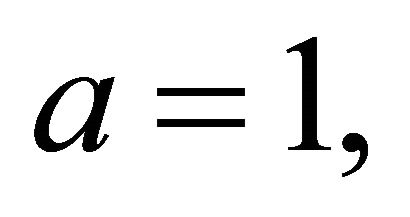 in this case
in this case  and therefore,
and therefore, 
Case 2.  in this case,
in this case,  and then
and then  , a contradiction, since
, a contradiction, since  is an even integer, while
is an even integer, while  is odd.
is odd.