1. Introduction
Based on the theory of inequalities, many classical inequalities not only promote the development of the inequality theory, but also lead to many applications in pure mathematics and in applied mathematics. Bernoulli’s inequality is one of the most distinguished inequalities. In this paper, a new proof of Bernoulli’s inequality via the dense concept is given. Some strengthened forms of Bernoulli’s inequality are established. Moreover, some equivalent relations between this inequality and other known inequalities are tentatively linked. The organization of this paper is as follows:
In Section 2, a new proof of Bernoulli’s inequality by means of the concept of density is raised. In Section 3, some strengthened forms of Bernoulli’s inequality are establised. In Section 4, we link some known inequalities which are equivalent to Bernoulli’s inequality. In Section 5, we collect some variants of Young’s inequality which are equivalent to Bernoulli’s inequality. For related results, we refer to [1-35].
2. Preliminaries
In order to complete these tasks, we need the definition and some basic results of the convex function as follows:
Definition 2.1
Let  be a function, where I is an interval of R.
be a function, where I is an interval of R.
1) Suppose that P and Q are any two points on the graph of , if the chord
, if the chord 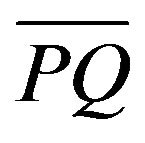 can not below the arc PQ of the graph of f, then we say that f is a convex function on I. That is, for any two point
can not below the arc PQ of the graph of f, then we say that f is a convex function on I. That is, for any two point 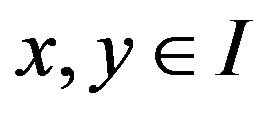 and any
and any ,
,
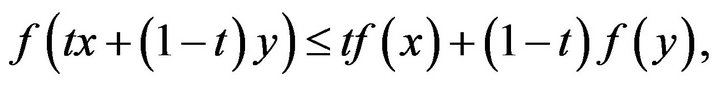 (1)
(1)
then f is a convex function on I. We say that f is called concave on I if  is convex on I.
is convex on I.
If, for any two points  with
with  and any
and any ,
,

then we say that 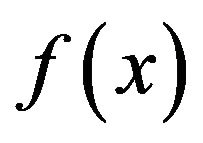 is a strictly convex function on I.
is a strictly convex function on I.
2) I is said to be midpoint convex or J-convex on I if for any two points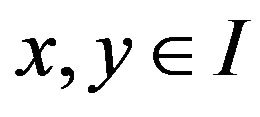 ,
,
 (2)
(2)
It is well-known fact that every convex function on an interval  is continuous; if f is mid-point convex and continuous on an interval I, then it is convex on I. The following Jensen’s inequality can be shown by the mathematical induction directly.
is continuous; if f is mid-point convex and continuous on an interval I, then it is convex on I. The following Jensen’s inequality can be shown by the mathematical induction directly.
Lemma 2.2 (Jensen’s inequality, [3], page 31) Let  be a convex function on I. Then for any
be a convex function on I. Then for any  with
with  and for any
and for any  ,
,
 (3)
(3)
If f is strictly convex, then (3) is strictly unless the  are all identically.
are all identically.
Lemma 2.3 Let  be a function. Then the following statements are equivalent:
be a function. Then the following statements are equivalent:
1) f is strictly convex on I2) For any two distinct points  and any
and any 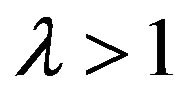 satisfying
satisfying 

3) For any two distinct points  and any
and any  satisfying
satisfying 

Proof 1) Þ 2). Let  be distinct and let
be distinct and let  be arbitrary. If
be arbitrary. If , then
, then
 and x is between y and z. It follows from the strict convexity of f on I that
and x is between y and z. It follows from the strict convexity of f on I that

Hence 2) holds.
2) Þ 3). Let  be distinct and let
be distinct and let  be arbitrary. If
be arbitrary. If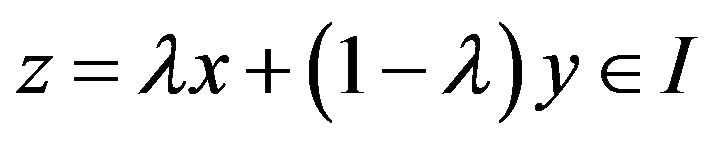 , then
, then
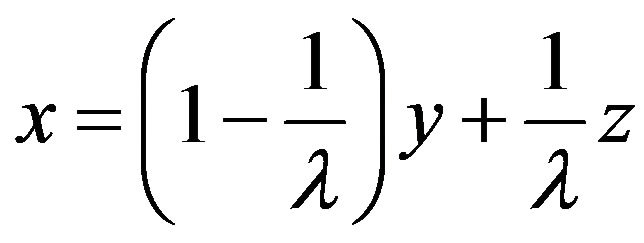 and both y and z are distinct. By the assumption of (b), we have
and both y and z are distinct. By the assumption of (b), we have

It follows from  that 3) holds.
that 3) holds.
3) Þ 1). Let  be distinct and let
be distinct and let  be arbitrary. If
be arbitrary. If , then
, then
 and
and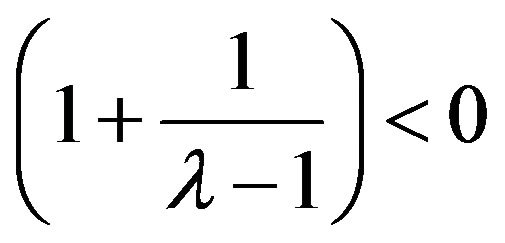 . It follows from the assumption of 3) that
. It follows from the assumption of 3) that

This prove 1) holds. Thus the proof is complete.
Next, we will prove Bernoulli’s inequality by means of the concept of density without differentiation or integration.
Lemma 2.4
 (4)
(4)
The equality is obvious for case x = 0 or for case  or 1.
or 1.
Proof Let

Claim 1: E is dense in .
.
It suffices to show that E satisfies the following three properties.
1) .
.
2) If , then
, then .
.
3) If , then
, then  and
and .
.
Let  be arbitrary with
be arbitrary with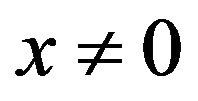 . Then
. Then
 and
and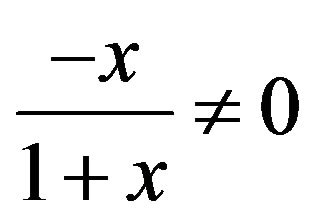 . Thus
. Thus

So, 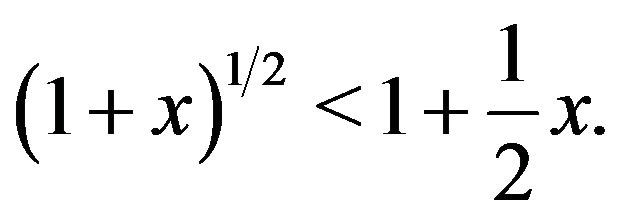 This proves 1) and hence E is nonempty.
This proves 1) and hence E is nonempty.
If , then
, then

This proves 2).
Next, if  are such that
are such that , then for every
, then for every  with
with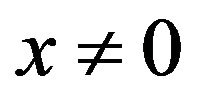 ,
,

This proves the first part of 3). On the other hand, it follows from  that
that
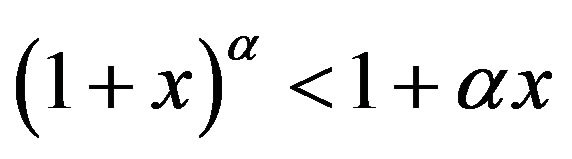
and

Therefore,
 (5)
(5)
Thus, we complete the proof of 3). Since 1)-3) imply that  for
for  and
and
 Therefore E must be dense in
Therefore E must be dense in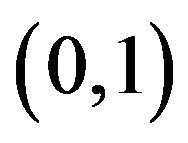 .
.
Finally, if  is arbitrary and
is arbitrary and  with
with , then for every
, then for every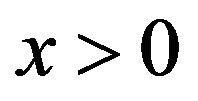 ,
,

This proves
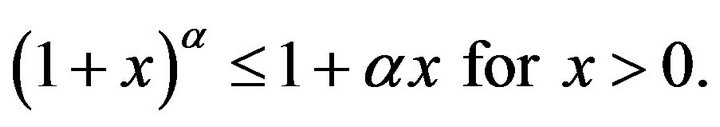
Similarly, if  is arbitrary and
is arbitrary and  with
with , then, for every
, then, for every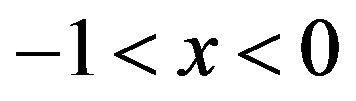 ,
,

This proves

Therefore, for every , we have
, we have
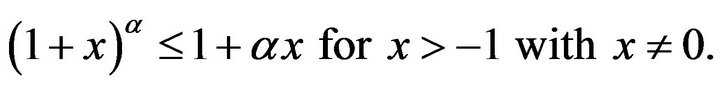
It follows from (5) again that (4) holds. This completes the proof.
Corollary 2.5 The following statements are equivalent:
1)  is strictly convex on
is strictly convex on 
2)  for all x, y > 0 with
for all x, y > 0 with  and for all
and for all 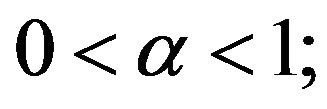
3) Young’s inequality holds, that is,
 where X, Y > 0 with
where X, Y > 0 with  and
and  with
with 
4) (4) holds.
Proof

The equality of Young’s inequality is clear for case  with
with . This completes the proof.
. This completes the proof.
Next, we prove some equivalent results which are related to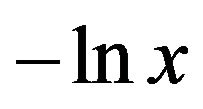 :
:
Lemma 2.6 For any , the following statements are equivalent:
, the following statements are equivalent:
1)  is strictly convex on
is strictly convex on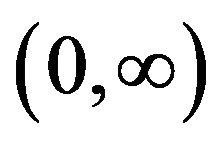 ;
;
2)  is strictly convex on
is strictly convex on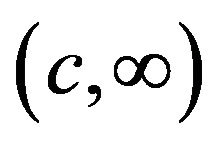 ;
;
3)  is strictly convex on
is strictly convex on .
.
Proof Clearly, 1) Þ 2) and 3).
Now, we prove 3) Þ 1) and 2) Þ 1). Let  be with
be with 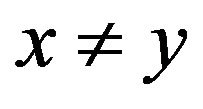 and let
and let  be arbitrary. Since
be arbitrary. Since

we have
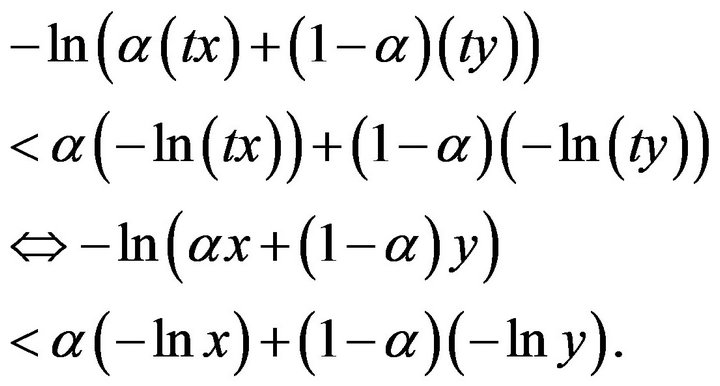
Thus, if t is small such that , we obtain that 3) implies 1). Similarly, if
, we obtain that 3) implies 1). Similarly, if  is enough large so that
is enough large so that , we obtain that 2) implies 1). This completes the proof.
, we obtain that 2) implies 1). This completes the proof.
Lemma 2.7 Let ,
, 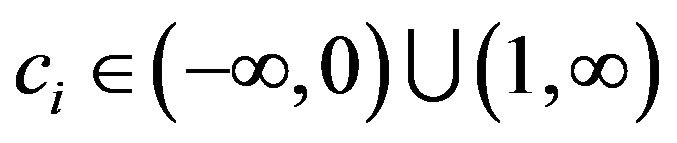 ,
, 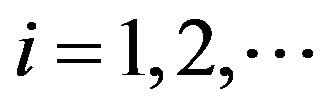 satisfying cixi, i = 1, 2, ··· be all positive or all negative. If, for all
satisfying cixi, i = 1, 2, ··· be all positive or all negative. If, for all  with
with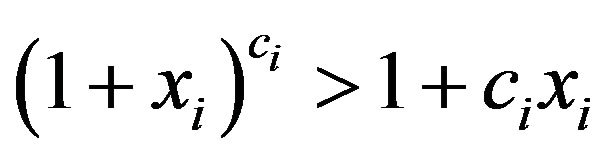 , then
, then

Proof This lemma is true for  by assumption. Suppose that this lemma holds for
by assumption. Suppose that this lemma holds for . Let
. Let
 . If
. If , then, clearly, the conclusion holds. Now, we assume
, then, clearly, the conclusion holds. Now, we assume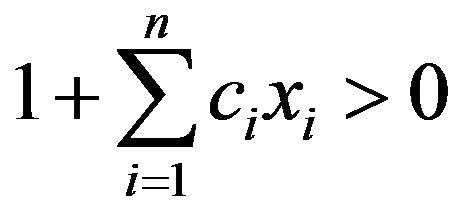 . Since
. Since ,
,
 are all positive or all negative, we see that
are all positive or all negative, we see that ,
, . Therefore,
. Therefore,
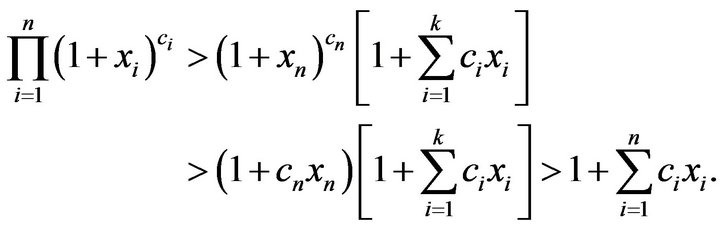
This completes our proof.
3. Variants of Bernoulli’s Inequality
In this section, we establish some variants of Bernoulli’s Inequality.
Since  is strictly concave and strictly increasing on
is strictly concave and strictly increasing on , its inverse function
, its inverse function  is strictly convex and strictly increasing. Using Lemma 2.7, we have the following Theorem 3.1 The following inequalities are equivalent:
is strictly convex and strictly increasing. Using Lemma 2.7, we have the following Theorem 3.1 The following inequalities are equivalent:

 is strictly convex on
is strictly convex on 

 , where
, where 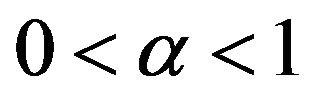 and
and , that is,
, that is,  , where
, where  and
and 
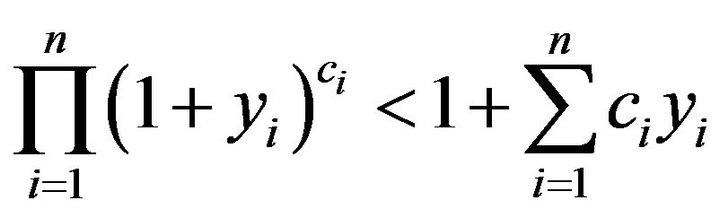
 , where
, where , 0 < yi,
, 0 < yi,  satisfy
satisfy 

 , where
, where  and
and , that is,
, that is,  , where
, where  and
and 
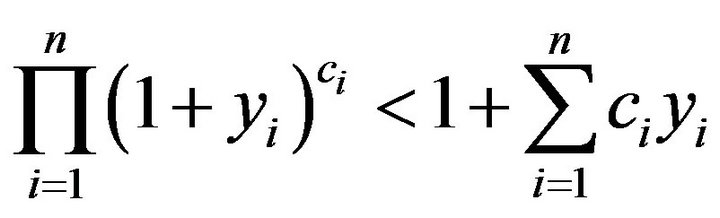
 , where
, where ,
,  ,
, 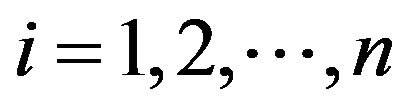 satisfy
satisfy 
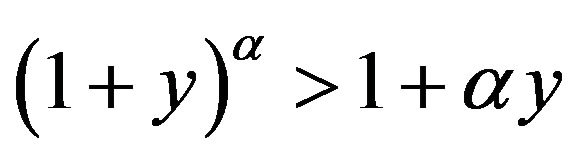
 , where
, where  and
and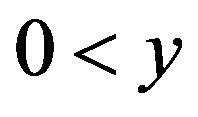 , that is,
, that is,  , where
, where  and
and 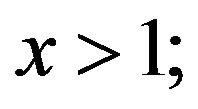

 , where
, where ,
, 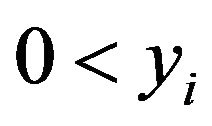 ,
, 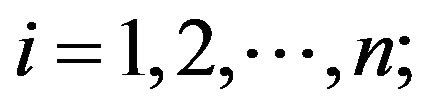

 , where
, where  and
and , that is,
, that is,  , where
, where  and
and 

 , where
, where ,
,  ,
, 

 , where
, where  and
and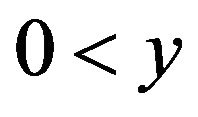 , that is,
, that is,  , where
, where 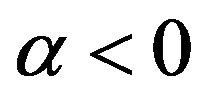 and
and 

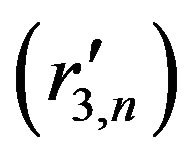 , where
, where  ,
,  ,
, 
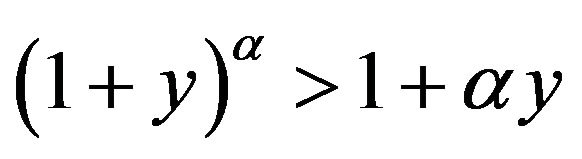
 , where
, where  and
and , that is,
, that is,  , where
, where  and
and 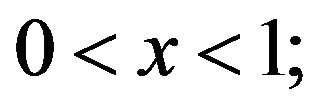
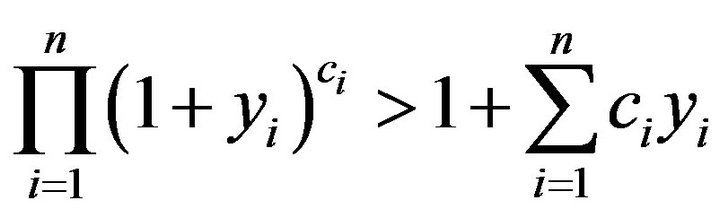
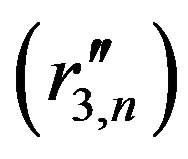 , where
, where ,
, 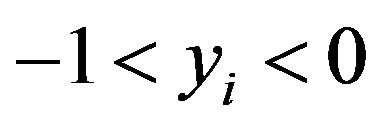 ,
, 

 , where
, where 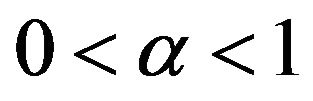 and y > 0;
and y > 0;

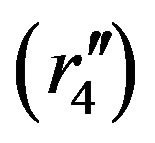 , where
, where  and
and 

 , where
, where  and
and 

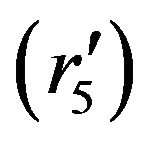 , where
, where  and
and 

 , where
, where  and
and 

 , where
, where  and
and 

 , where
, where  and y > 0;
and y > 0;
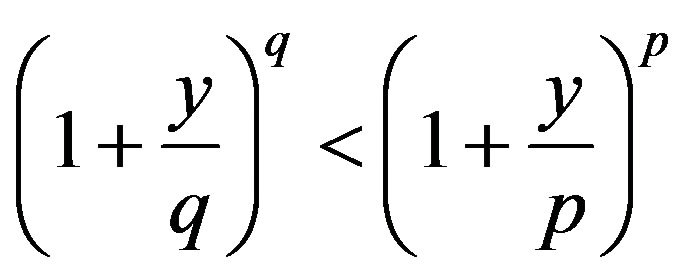
 , where
, where 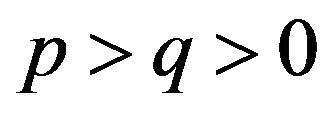 and
and 
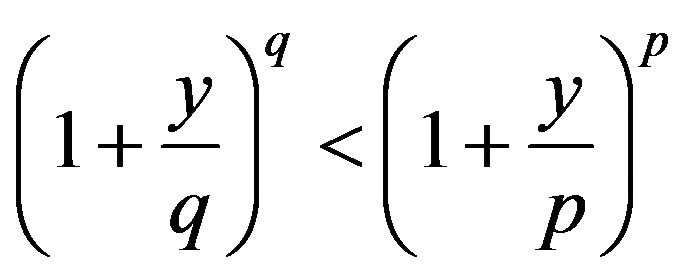
 , where
, where 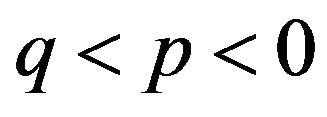 and
and 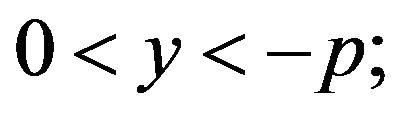

 , where
, where  and y < 0;
and y < 0;
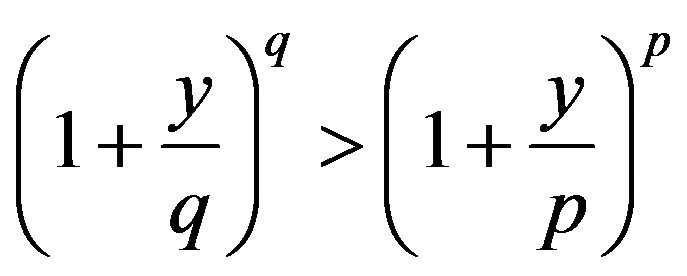
 , where
, where  and
and ;
;
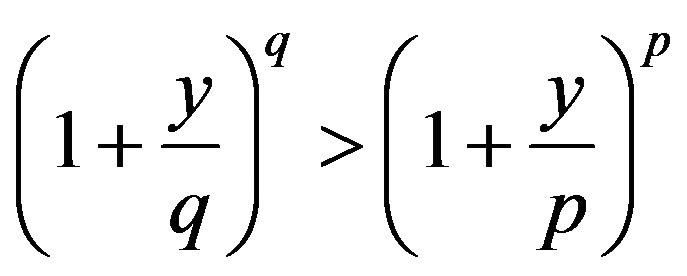
 , where
, where  and
and .
.
Proof Let , where
, where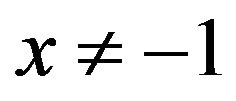 , then
, then ,
,  ,
, 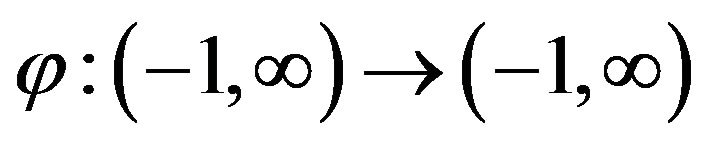 is a strictly convex function,
is a strictly convex function,  and
and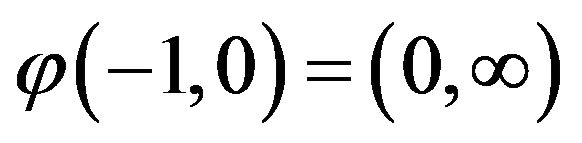 .
.
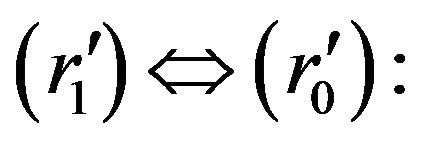





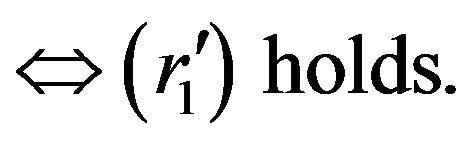
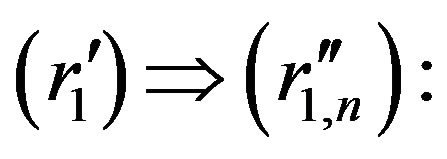 Let
Let . WLOG, we assume y1 > y2 > 0 and
. WLOG, we assume y1 > y2 > 0 and . Then
. Then
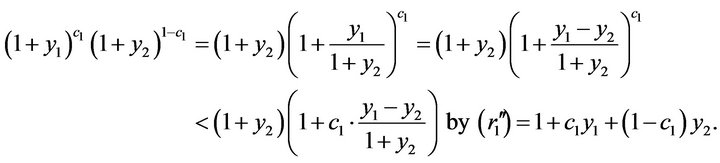
Now, we assume  holds for
holds for 
 . Set
. Set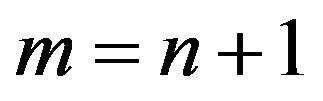 . We have for
. We have for  and
and  with
with . Let
. Let . It follows from above argument and the induction assumption that
. It follows from above argument and the induction assumption that

This proves .
.  is obvious.
is obvious.
Moreover, it follows from Lemma 2.7 that ,
,  ,
, 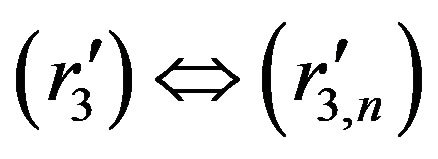 and
and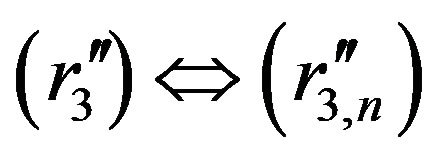 .
.
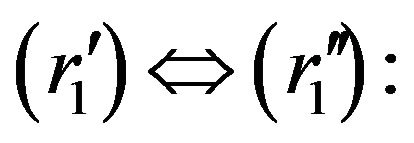 By
By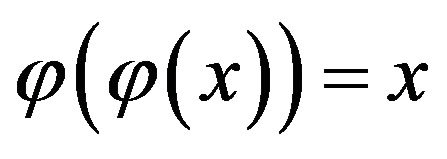 ,
,  and
and ,
,
 holds
holds





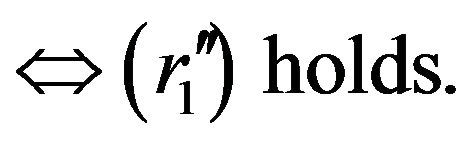

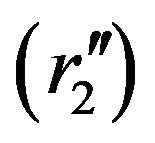 holds
holds
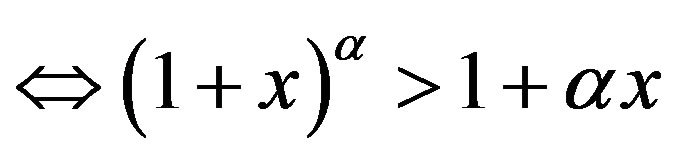 , where
, where  and
and 
 , where
, where  and
and 
 , where
, where  and
and 
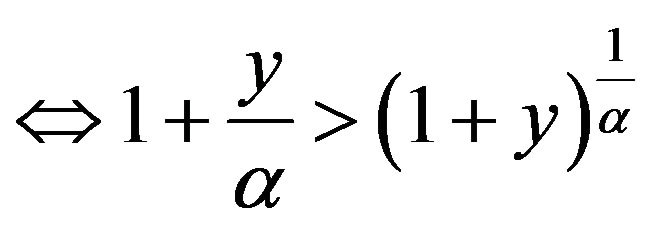 , where
, where  and
and 
 holds.
holds.
 holds
holds
 , where
, where  and
and 
 , where
, where  and
and 
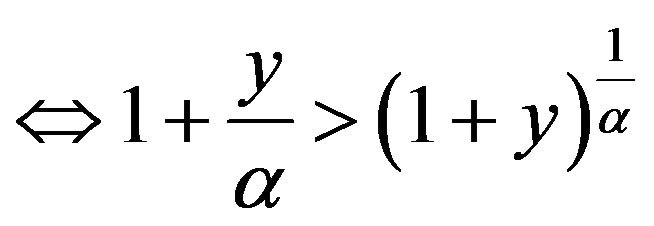 , where
, where  and
and 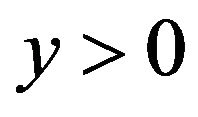
 holds.
holds.
 holds
holds
 , where
, where  and
and 
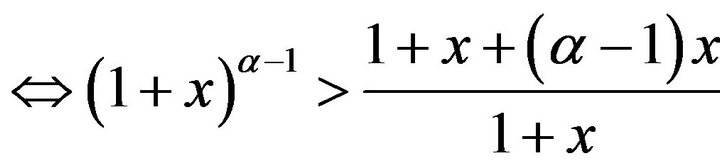 , where
, where  and x > 0
and x > 0
 , where
, where  and
and 
 holds.
holds.
 It follows from
It follows from  that
that
 holds
holds
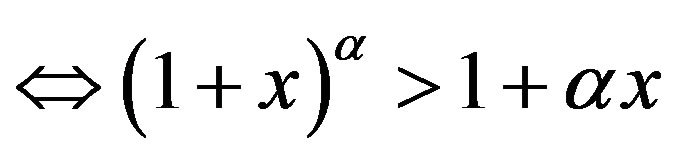 , where
, where  and
and 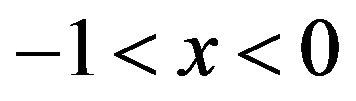
 , where
, where  and
and 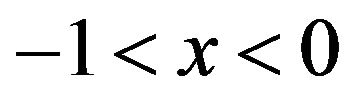
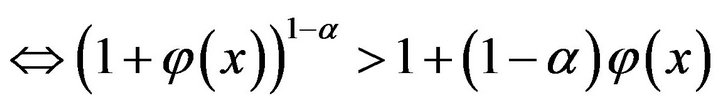 , where
, where  and
and 
 holds.
holds.
 holds
holds
 , where
, where  and
and 
 , where
, where  and
and 
 , where
, where  and
and 
 holds.
holds.
 holds
holds
 , where
, where  and
and 
 , where
, where  and x > 0
and x > 0
 holds.
holds.
 holds
holds
 , where
, where 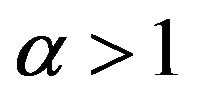 and
and 
 , where
, where  and
and 
 , where
, where  and
and 
 holds.
holds.
 It follows from
It follows from  and
and , where
, where , that
, that  holds
holds
 , where
, where  and
and 
 , where
, where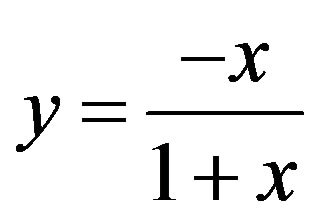 ,
,  and
and 
 holds.
holds.
 holds
holds
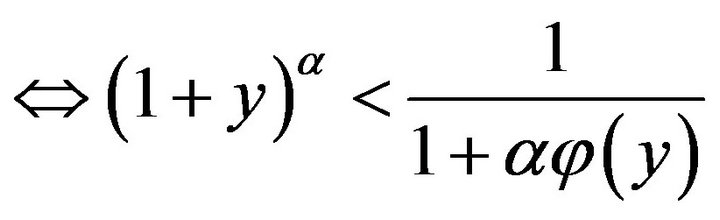 , where
, where  and
and 
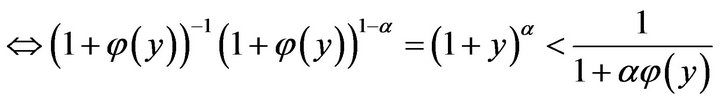 , where
, where  and
and 
 , where
, where  and
and 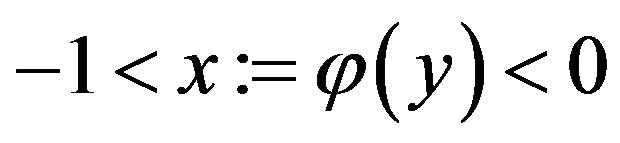
 holds.
holds.
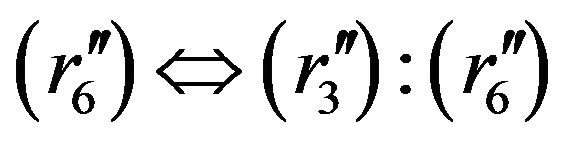 holds
holds
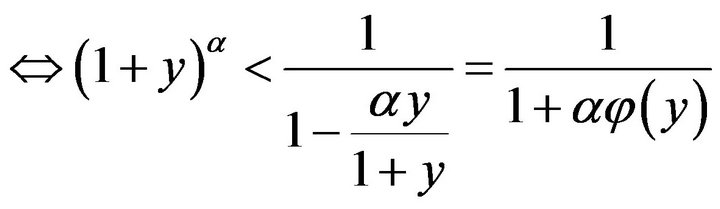 , where
, where  and
and 
 , where
, where 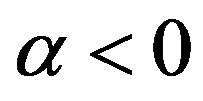 and
and 
 , where
, where  and
and 
 , where
, where  and
and 
 holds.
holds.
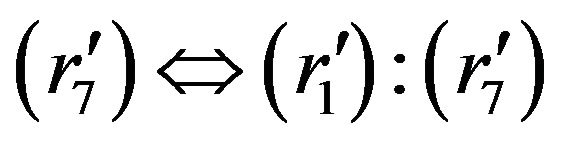 holds
holds
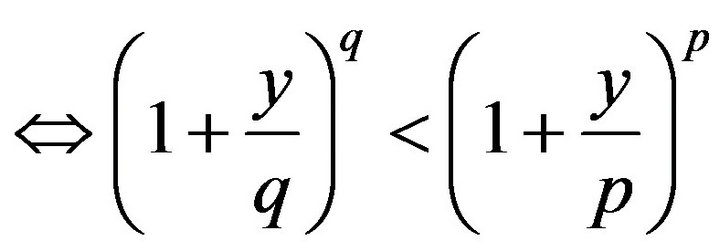 , where
, where 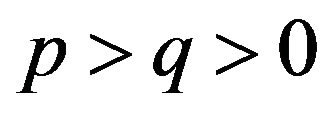 and
and 
 , where
, where  and
and 
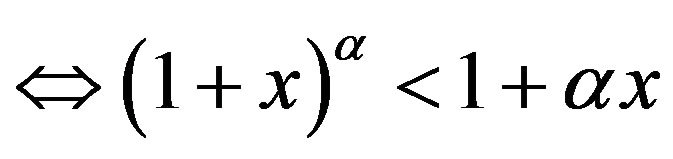 , where
, where  and x > 0
and x > 0
 holds.
holds.
 holds
holds
 , where
, where  and
and 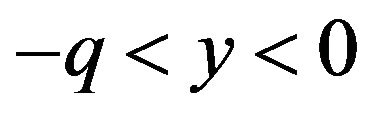
 , where
, where 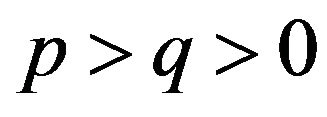 and
and 
 , where
, where , −1 < x < 0
, −1 < x < 0
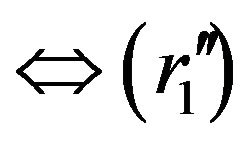 holds.
holds.
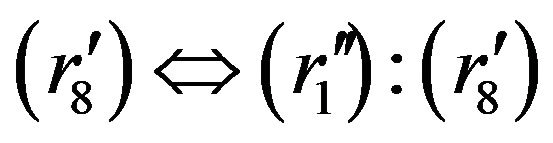 holds
holds
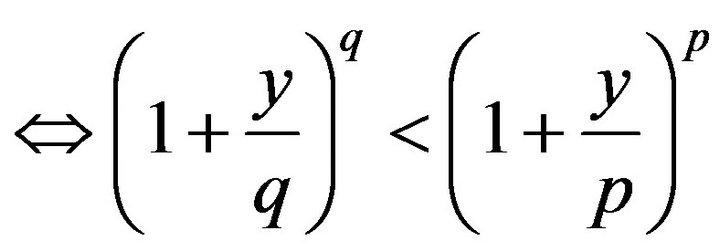 , where
, where  and
and 
 , where
, where 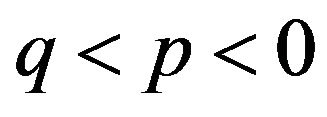 and
and 
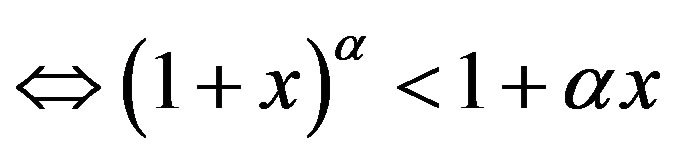 , where
, where 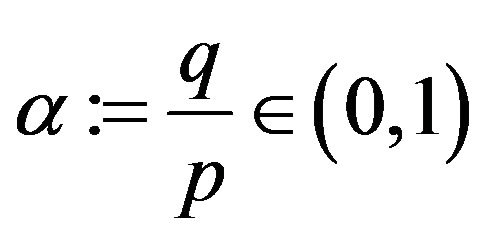 and
and 
 holds.
holds.
 holds
holds
 , where
, where  and
and 
 , where
, where 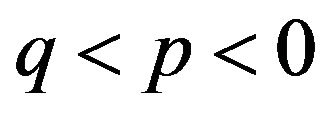 and
and 
 , where
, where  and x > 0
and x > 0
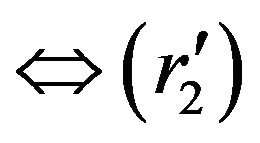 holds.
holds.
 holds
holds
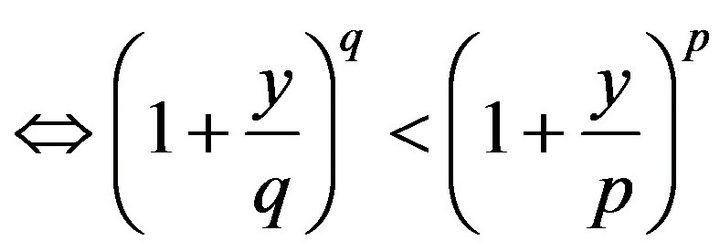 , where
, where  and
and 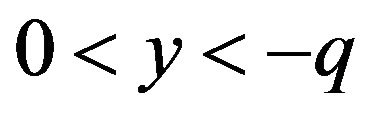
 , where
, where  and
and 
 , where
, where  and
and 
 holds.
holds.
 holds
holds
 , where
, where 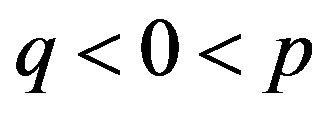 and
and 
 , where
, where  and
and 
 , where
, where  and
and 
 holds.
holds.
This prove our Theorem.
By Theorem 3.1, we have the following Corollary 3.2 Let  be a constant. If
be a constant. If  and
and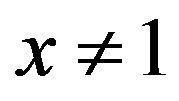 , then the following three inequalities are equivalent:
, then the following three inequalities are equivalent:
1) 2)
2) 3)
3) 
Proof Clearly, it follows from Theorem 3.1 that 1) holds 
 and
and  hold;
hold;
2) holds 
 and
and  hold;
hold;
3) holds 
 and
and  hold.
hold.
4. Main Results
Now, we can state and prove some inequalities which are equivalent to each other in the following Theorem 4.1 Let ,
,
 , and
, and , where n is a positive integer. Then the following some statements are equivalent:
, where n is a positive integer. Then the following some statements are equivalent:

 , where
, where  and
and 

 , where
, where  and
and 
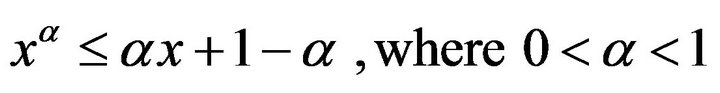
 and
and 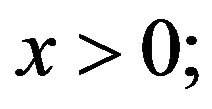

 , where
, where ,
, 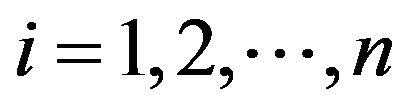 and
and 

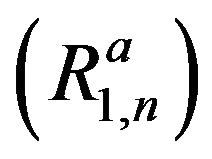 , where
, where  and
and ,
, 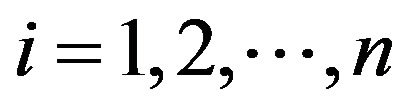 ,
, 

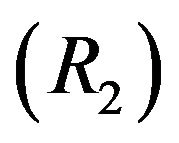 , where
, where  and
and 

 , where
, where  and
and  or
or 

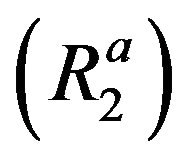

 and
and 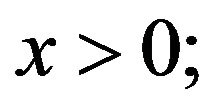

 , where
, where  and
and ,
, 

 , where
, where  and
and 
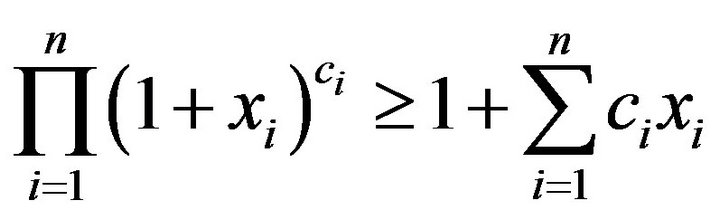
 , where
, where 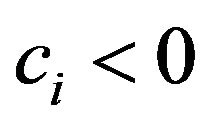 and
and 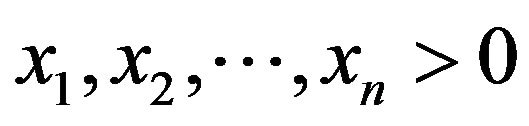 or
or 



 and
and 

 , where
, where  and
and ,
, 

 , where
, where  and
and 

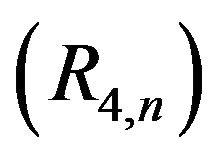 where
where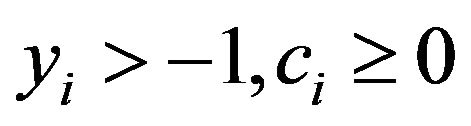 ,
,  and
and 

 , where
, where  and
and 
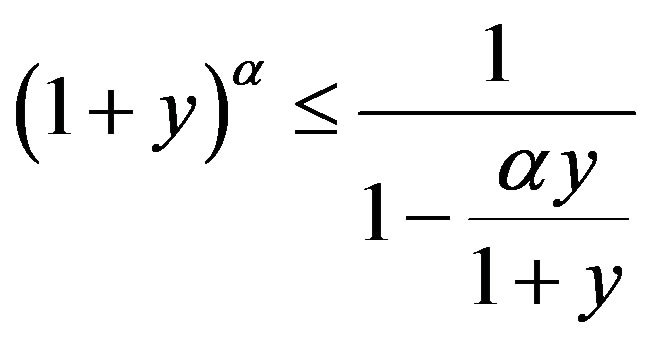
 , where
, where  and
and 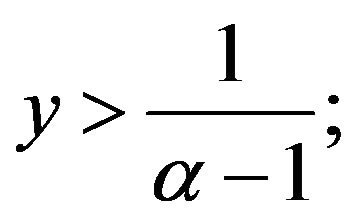

 , where
, where 

 is convex on
is convex on 

 , where
, where 

 , where
, where 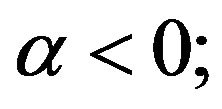

 , where
, where  and
and , hence
, hence , where
, where 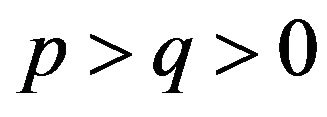 and
and . Thus,
. Thus,  is an increasing function of q, where
is an increasing function of q, where  and
and 

 , where q < p < 0 and
, where q < p < 0 and 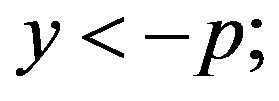 hence
hence , where p > q > 0 and y < q;
, where p > q > 0 and y < q;

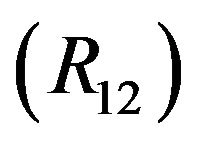 , where
, where 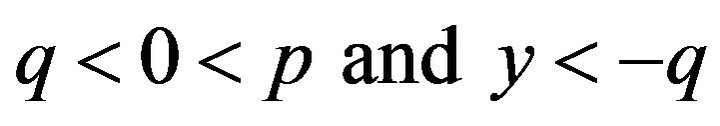 or
or  and
and 

 , where
, where 

 , where
, where 

 if
if  with
with  (Hölder’s inequality);
(Hölder’s inequality);

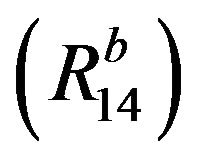 (Cauchy’s inequality);
(Cauchy’s inequality);

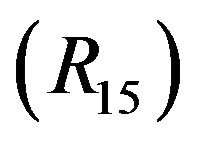 , where
, where 
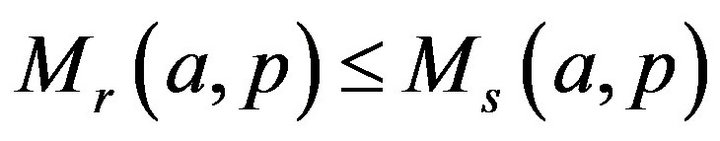
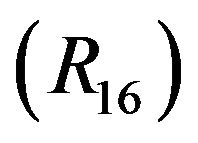 , where
, where ,
,

Here 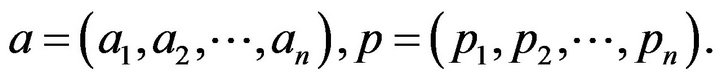 In particular,
In particular,
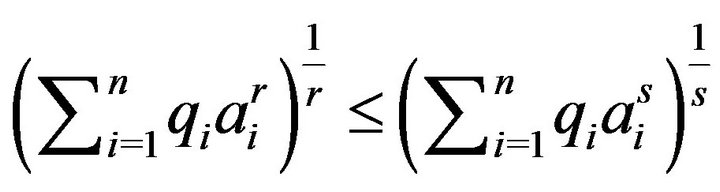
 ,
,  (Schlömich’s inequality);
(Schlömich’s inequality);
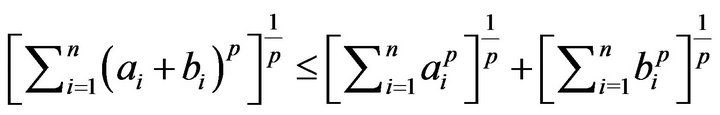
 for
for 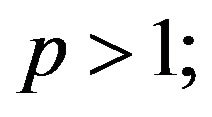 (Minkowski’ inequality)
(Minkowski’ inequality)

 for
for 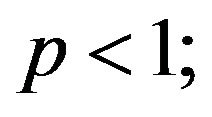 (Minkowski’ inequality)
(Minkowski’ inequality)
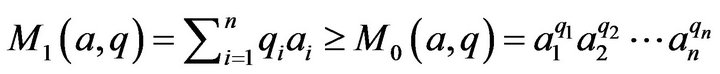
 , hence
, hence  where
where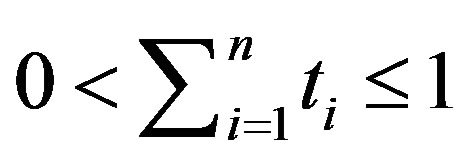 .
.
In general,  (AGM inequality)
(AGM inequality)

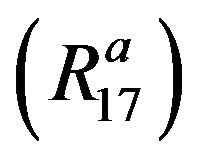
 Shanon’s inequality:
Shanon’s inequality: 
 (see [7])
(see [7])  where
where ,
,  ,
, 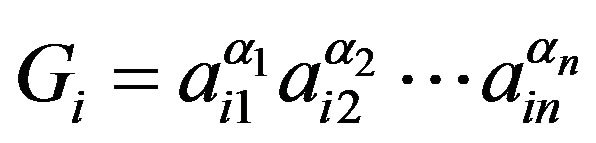 ,
, 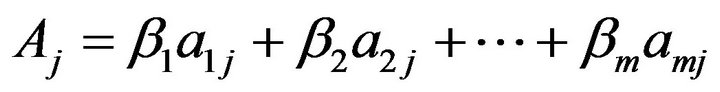 ,
,  , see the following figure:
, see the following figure:

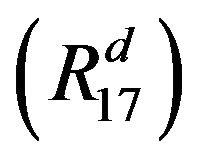

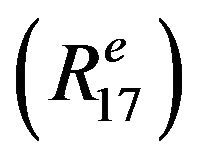 where
where 
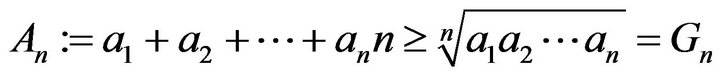
 , which is equivalent to
, which is equivalent to 



 , where
, where  are positive integers,
are positive integers,  and
and , that is,
, that is,  , where
, where 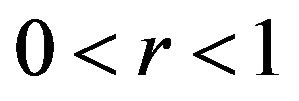 is a rational number;
is a rational number;

 , where
, where 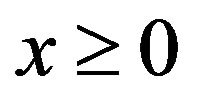 and
and 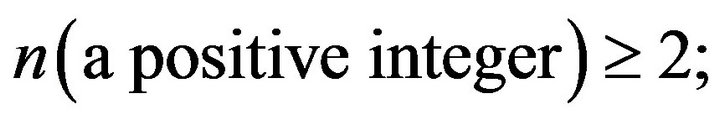
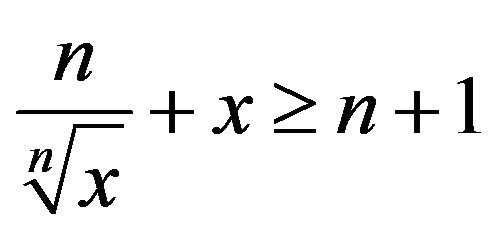
 , where
, where 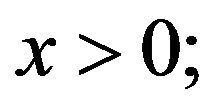

 ,
, 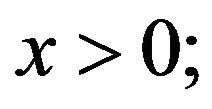
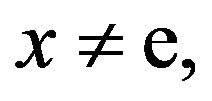

 is (strictly) increasing on
is (strictly) increasing on 
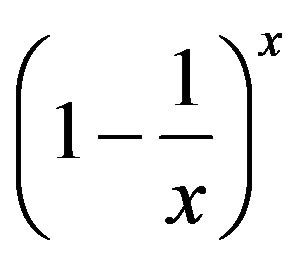
 is (strictly) increasing on
is (strictly) increasing on 

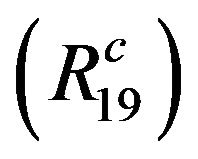 is (strictly) decreasing on
is (strictly) decreasing on 

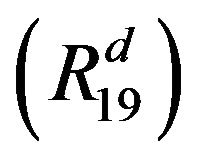 ,
,  , where
, where 

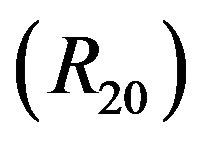 , where
, where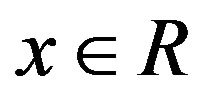 , it has following some variants:
, it has following some variants:
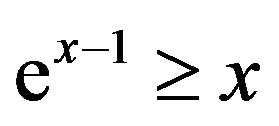
 , where
, where 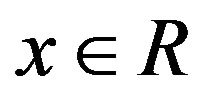

 , where
, where ,
,
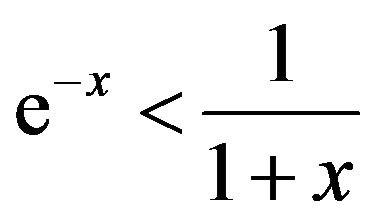
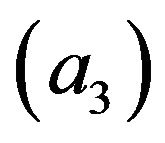 , where
, where ,
,

 or
or , where
, where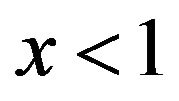 ,
,

 , where
, where ,
,
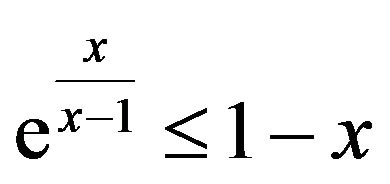
 , where
, where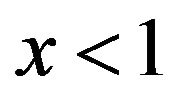 ,
,
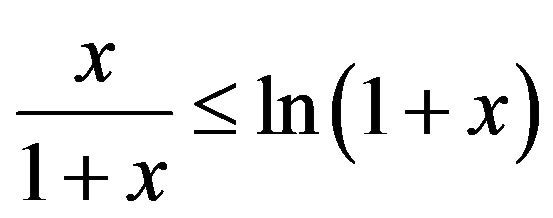
 , where
, where ,
,
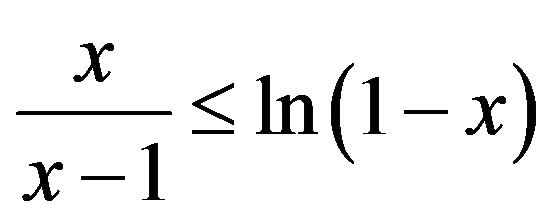
 , where
, where ,
,

 , where
, where ,
,

 , where
, where  or
or ,
,

 , where
, where ,
,  ,
,

 , where
, where ,
,  ,
,
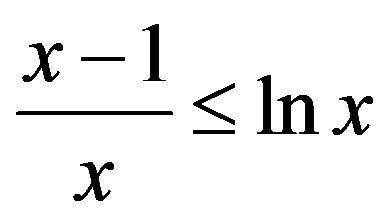
 , where
, where ,
,
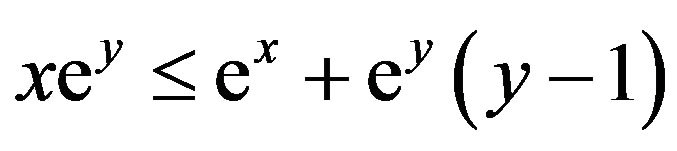
 , where
, where ,
,

 , where
, where  and
and 
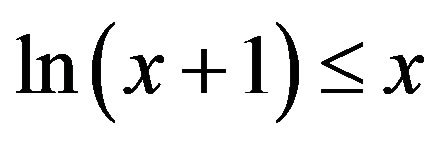
 , where
, where , that is,
, that is,  , where
, where 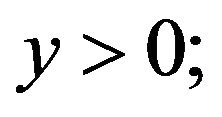

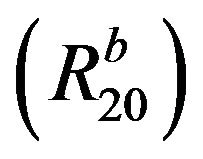 , where
, where 

 , where
, where  or
or  that is,
that is,  ,
, 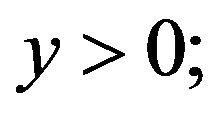

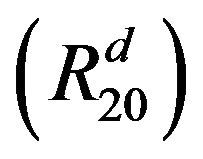 , where
, where  that is
that is ,
,  and
and 

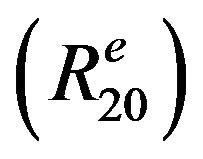 , where
, where 

 , where
, where 

 , where
, where , that is,
, that is,  (Jacobsthal’s inequality);
(Jacobsthal’s inequality);
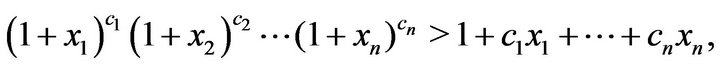
 where
where  and
and  or
or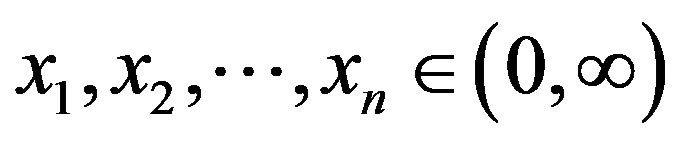 .
.
Proof Taking  in Corollary 3.2, we see that
in Corollary 3.2, we see that ,
,  and
and  are equivalent. Similarly, replacing x by
are equivalent. Similarly, replacing x by  in Corollary 2.2, we get that
in Corollary 2.2, we get that ,
,  and
and 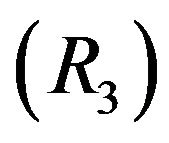 are equivalent. Hence, it follows from Theorem 3.1 that
are equivalent. Hence, it follows from Theorem 3.1 that ,
, 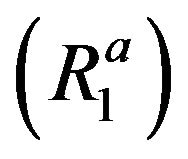 ,
,  ,
, 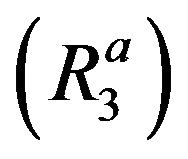 and
and  are equivalent. If
are equivalent. If , then, clearly,
, then, clearly,
 ,
,  ,
,  ,
, 
 ,
, .
.
 with i = 1, 2, 3 follows by taking y = x + 1.
with i = 1, 2, 3 follows by taking y = x + 1.
 : We see that
: We see that 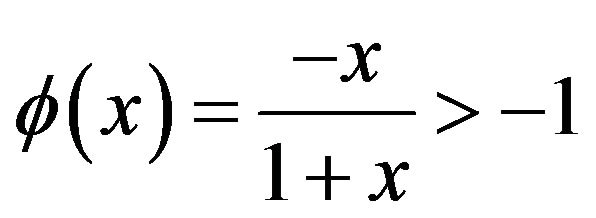 iff x > −1. Hence
iff x > −1. Hence

Similarly, we can prove .
.
 follows from
follows from  and
and  in Theorem 3.1.
in Theorem 3.1.
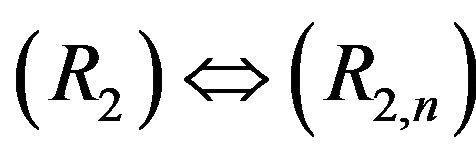 and
and  follows from Theorem 3.1 too.
follows from Theorem 3.1 too.
 : Let
: Let ,
, 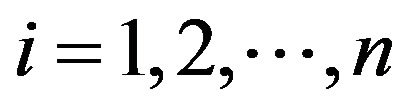 satisfy
satisfy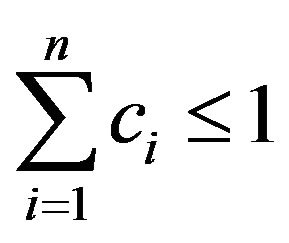 . By
. By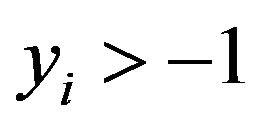 , we see that
, we see that . Thus, it follows from
. Thus, it follows from 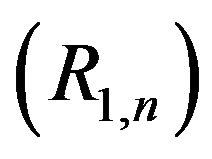 that
that
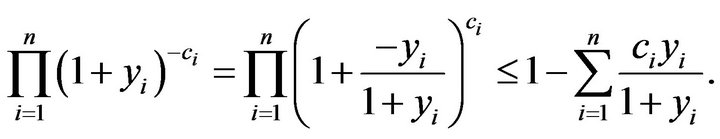
Hence  holds.
holds.
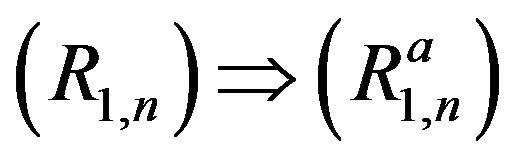 by replacing yi and ci by
by replacing yi and ci by , respectively.
, respectively.
Similarly, we can prove .
.
 : Let
: Let ,
,  , where
, where , then
, then . It follows from
. It follows from  that
that
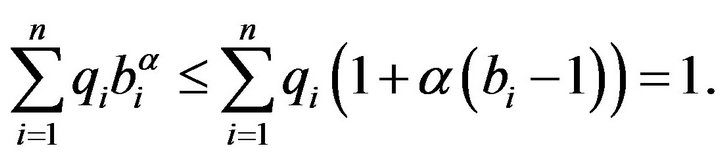
Hence,

This completes the proof of .
.
 , see Hardy etc. ([8], Theorem 9, 11 and 16).
, see Hardy etc. ([8], Theorem 9, 11 and 16).
 : It follows from
: It follows from  and
and  that
that

Thus,  (see Maligrands [18] or Rooin [28]). Hence,
(see Maligrands [18] or Rooin [28]). Hence,

Therefore,  holds.
holds.
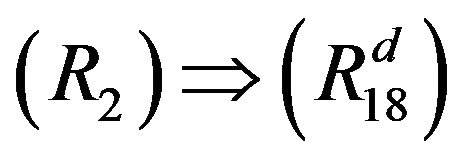 : Taking
: Taking  and
and 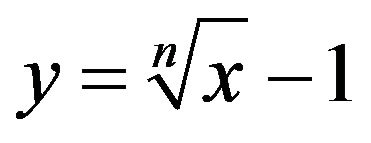 in
in , we see that
, we see that

Hence
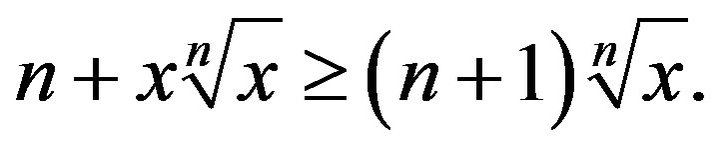
Dividing both sides by , we get
, we get .
.
 is clear.
is clear.
 : We show
: We show  by mathematical induction on n. If
by mathematical induction on n. If , then
, then  is obvious by
is obvious by .
.
Suppose  holds for
holds for  with
with .
.
Set n = m + 1. If , it is easy to see that each
, it is easy to see that each  by the assumption, and hence
by the assumption, and hence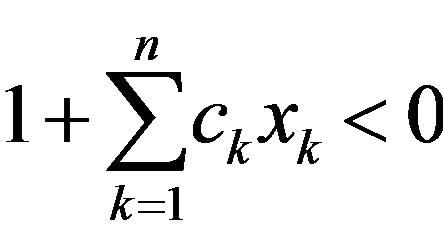 . Therefore
. Therefore 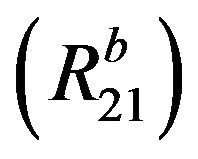 holds. Assume
holds. Assume . Since
. Since , we have
, we have

Thus  holds.
holds.
 : Taking
: Taking  and
and  in
in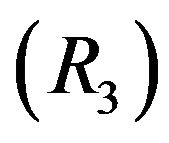 , we see that
, we see that  holds.
holds.
 : Clearly,
: Clearly,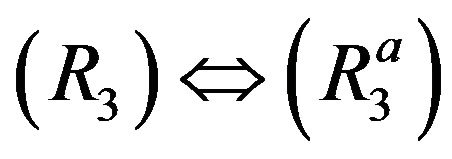 . Let
. Let ,
, 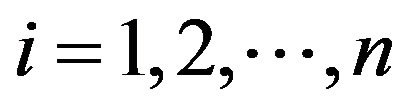 such that
such that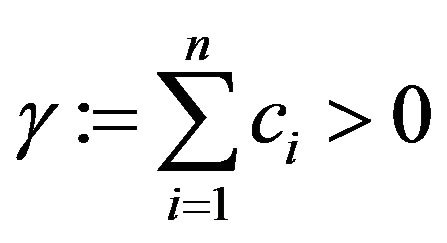 . If
. If , then it follows from
, then it follows from  that
that
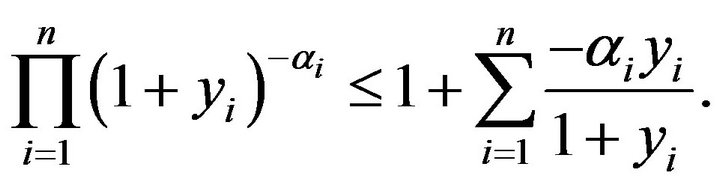 (5)
(5)
By  and
and ,
,  ,
,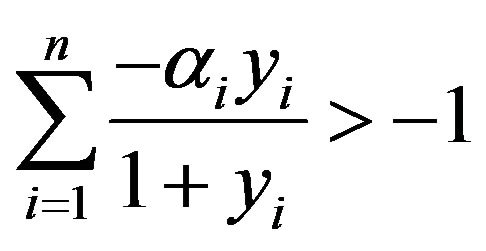 . Clearly,
. Clearly,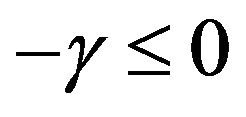 . By (5) and
. By (5) and ,
,

Thus,  is proved.
is proved.
 : Let
: Let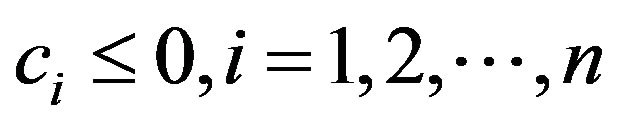 . If
. If , then
, then . By
. By ,
,

This completes the proof of .
.
 : Without loss of generality, we my assume that x, y > 0 and
: Without loss of generality, we my assume that x, y > 0 and . Since
. Since  is strictly increasing,
is strictly increasing,

By the definition of the convex function,  .
.
 : Taking
: Taking  and
and  in
in , we see that
, we see that  holds.
holds.
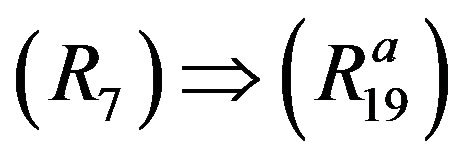 : Let
: Let . Then, by
. Then, by ,
,
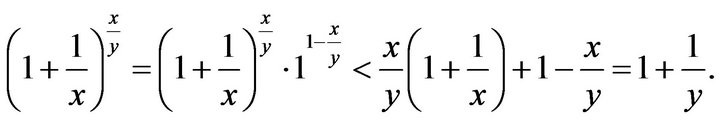
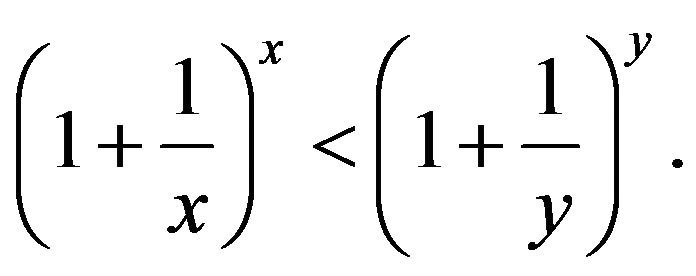
 Let
Let . Then, by
. Then, by ,
,


 : Let
: Let . Then, by
. Then, by ,
,

Hence

and so

 : If
: If , then, by
, then, by ,
,

Replacing  by
by ,
,

Thus,  is proved.
is proved.
Similarly, we can prove .
.
 : Let
: Let , then, by
, then, by ,
,

Replacing  by
by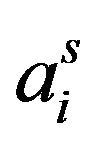 ,
,

Hence
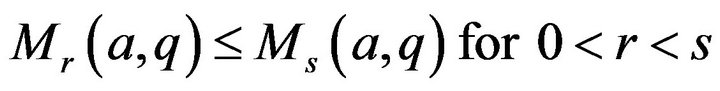
and

f , then
, then ,
, . If
. If , then
, then ,
, . Hence,
. Hence,

It follows by taking  that
that  holds.
holds.
Similarly, we can prove ,
, .
.
 : Let
: Let . Replacing
. Replacing  and
and
 by
by  and
and  in
in , respectively, for
, respectively, for , we obtain
, we obtain  thus, we complete the proof.
thus, we complete the proof.
 follows by taking p = q = 2 in
follows by taking p = q = 2 in .
.
 : Let
: Let  and
and
 for
for . Then, it follows from
. Then, it follows from  that
that

Thus,  is midconvex on
is midconvex on , and hence
, and hence 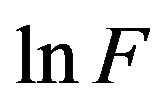 is convex on
is convex on . Hence, for any
. Hence, for any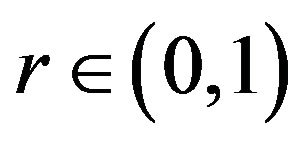 ,
,

which implies
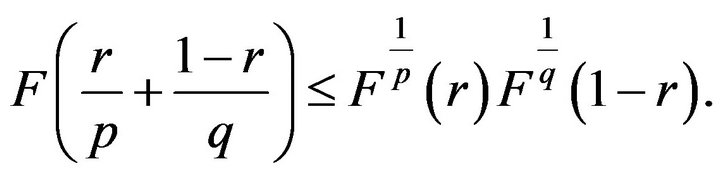
Letting  in the both sides of the above inequality,
in the both sides of the above inequality,

This shows that  holds, see Li and Shaw [15].
holds, see Li and Shaw [15].
 : Let
: Let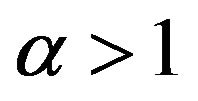 , ai > 0, qi ≥ 0,
, ai > 0, qi ≥ 0,  and
and ,
,  , where
, where . Thus
. Thus . By
. By ,
,
 (6)
(6)
It follows from (6) and

that

Hence, 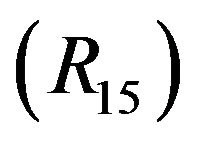 holds.
holds.
 : Let
: Let . Then, by
. Then, by ,
,
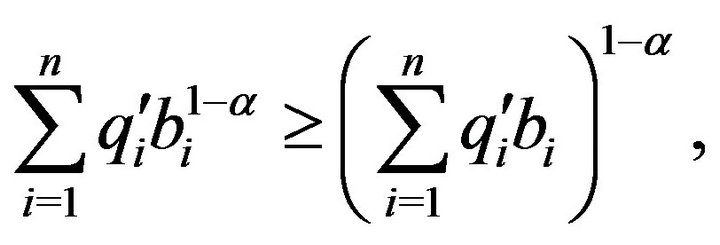
where 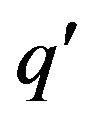 and
and  are defined as above. Hence,
are defined as above. Hence,

Thus,

This completes the proof of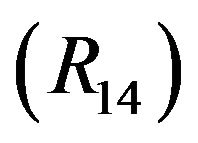 .
.
 : Taking
: Taking  and replacing ai by
and replacing ai by  in
in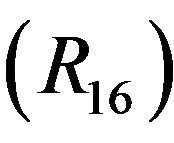 , for
, for  we obtain
we obtain .
.
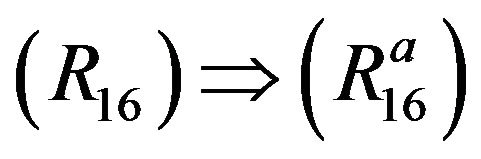 follows by taking
follows by taking  in
in  for
for .
.
 : Taking
: Taking  and replacing
and replacing  by
by  in
in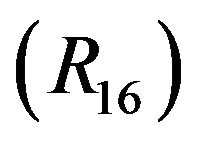 , for
, for 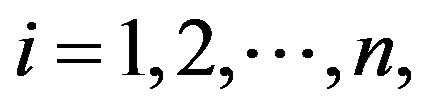 thus we complete the proof.
thus we complete the proof.
 : see p. 55 of Mitrinovic [19]. Similarly, we can prove
: see p. 55 of Mitrinovic [19]. Similarly, we can prove .
.
 follows by taking
follows by taking  in
in .
.
 follows by taking
follows by taking 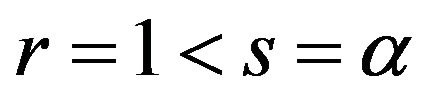 in
in .
.
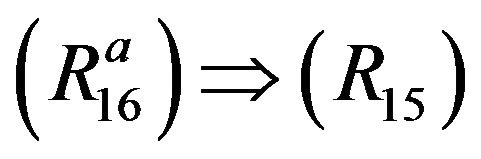 follows by taking
follows by taking  in
in .
.
 follows by taking
follows by taking  in
in 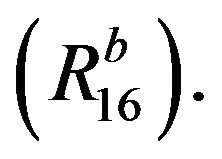
 follows by taking
follows by taking 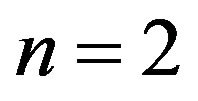 and
and  in
in 
 ,
, 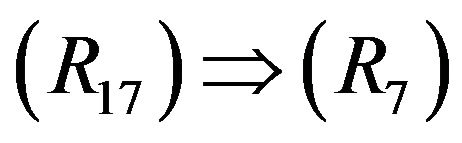 (with
(with ) and
) and  (with
(with ) are clear.
) are clear.
 : Replacing
: Replacing  by
by  in
in , we proved
, we proved . Similarly, we can prove
. Similarly, we can prove .
.
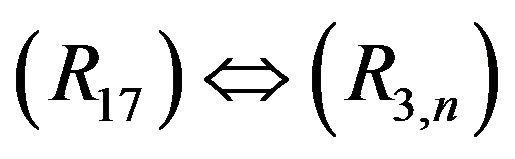 : Taking
: Taking ,
,  ,
, 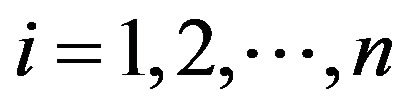 ,
,  ,
,  , and
, and , we see easily that both
, we see easily that both  and
and  are equivalent.
are equivalent.
 : Without loss of generality, we may assume that
: Without loss of generality, we may assume that ,
, . Thus, by
. Thus, by ,
,
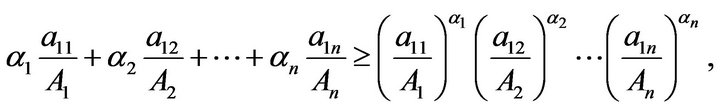
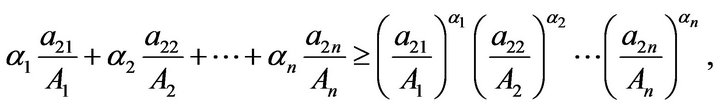

Hence,
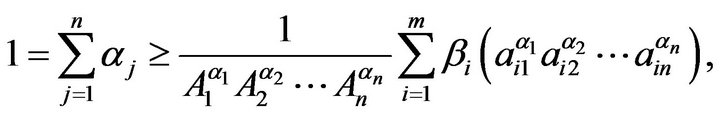
This completes the proof of .
.
 : Taking the natural logarithm in the both sides of
: Taking the natural logarithm in the both sides of , we get
, we get . Conversely, deleting the natural logarithm of the both sides of
. Conversely, deleting the natural logarithm of the both sides of , we get
, we get .
.
 : Taking
: Taking  in
in , we get
, we get .
.
 : Taking
: Taking  in
in , we see that
, we see that 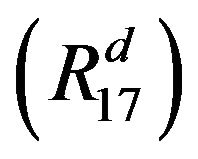 holds.
holds.
 : Taking
: Taking  in
in , we get
, we get .
.
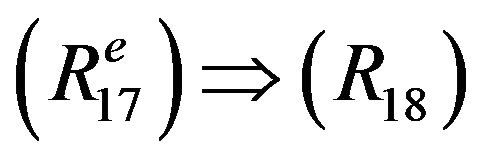 : Taking
: Taking ,
,  in
in  and using the following figure, we get
and using the following figure, we get .
.

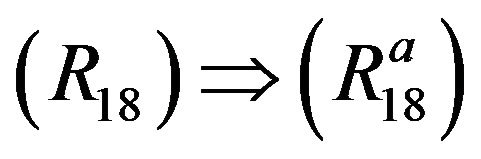 is clear.
is clear.
 : Taking
: Taking  and
and  in
in , we get
, we get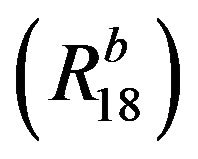 .
.
 (see [33]): It follows from
(see [33]): It follows from  that
that 
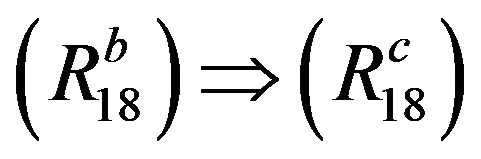 follows by taking
follows by taking  and
and  in
in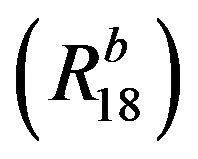 .
.
 : Let
: Let . Then, by
. Then, by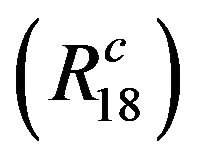 ,
, 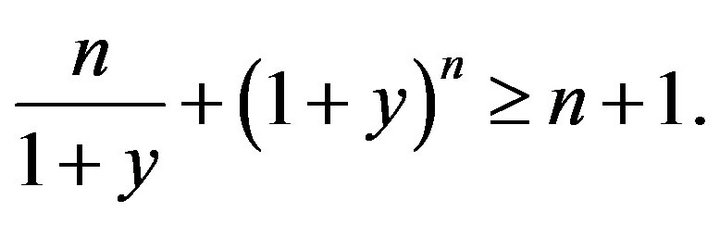
Thus, . Clearly, if
. Clearly, if , then the above inequality holds too.
, then the above inequality holds too.
 : Clearly, if
: Clearly, if , then
, then  holds.
holds.
Suppose that  holds for
holds for . Thus, for
. Thus, for , if
, if , then
, then . Hence
. Hence . This and
. This and  complete the proof of
complete the proof of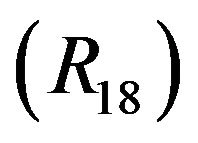 .
.
 : If
: If , then
, then . Therefore, by
. Therefore, by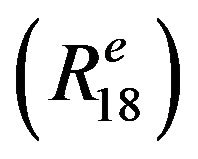 ,
,

Thus,

Thus,  holds.
holds.
 Let
Let . Then
. Then ,
, . Thus,
. Thus,
 holds, that is,
holds, that is,  is a strictly increasing function on
is a strictly increasing function on .
.
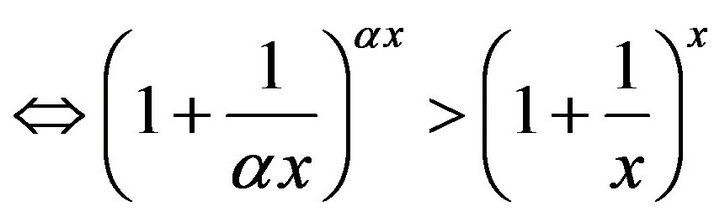 , where
, where 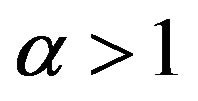 and
and 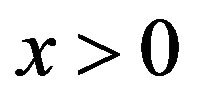
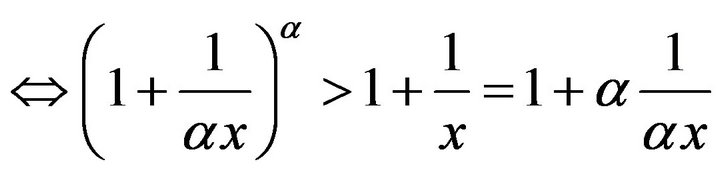 ,
, 

 holds by Theorem 1.
holds by Theorem 1.
 holds, that is,
holds, that is, 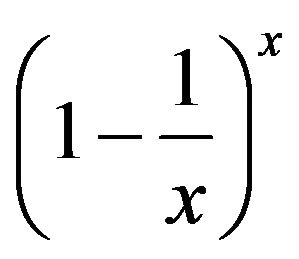 is a strictly increasing function on
is a strictly increasing function on .
.
 , where
, where  and
and 
 ,
,  ,
, 
 ,
,  ,
, 
 holds by Theorem 3.1.
holds by Theorem 3.1.
 holds, that is,
holds, that is,  is a strictly increasing function on
is a strictly increasing function on .
.
 is a strictly increasing function on
is a strictly increasing function on .
.
 is a strictly increasing function on
is a strictly increasing function on .
.
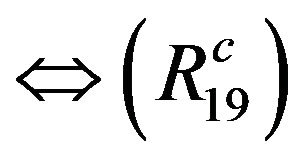 holds.
holds.
Thus, 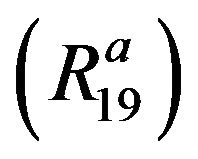 ,
,  and
and  are equivalent.
are equivalent.
 : For all
: For all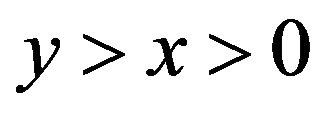 , since
, since  and
and  are equivalent,
are equivalent,

In particular, for all x > 0,  and
and

approaches to 0 as . Thus, by
. Thus, by ,
,  and
and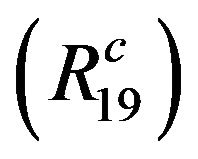 , we get
, we get , see [2].
, see [2].
 : By the first inequality of
: By the first inequality of ,
,

Hence,

By the second inequality of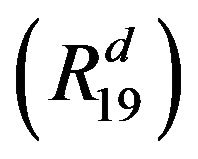 ,
,

Hence,

It follows from  for
for  that, for each
that, for each 

If  or
or , then, clearly,
, then, clearly,  holds. This completes the proof of
holds. This completes the proof of .
.
 : By
: By ,
,
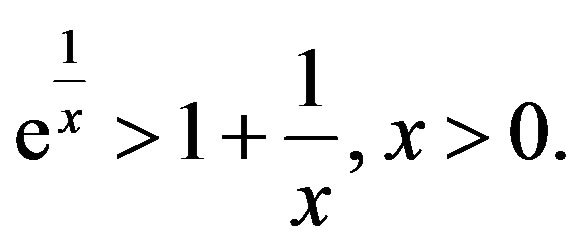
Hence,  ,
,  , that is, the first inequality of
, that is, the first inequality of  holds. Next, by
holds. Next, by ,
,
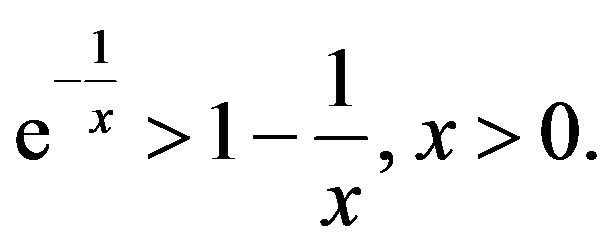
Hence, if , then
, then

where  Thus, the second inequality of
Thus, the second inequality of 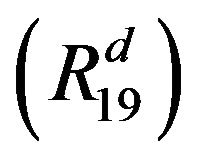 holds.
holds.
 is clear.
is clear.
 : Taking
: Taking  in
in  of
of ,
,

where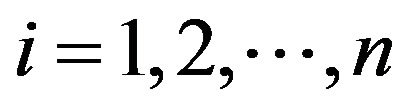 . Summing this n inequalities, we get
. Summing this n inequalities, we get  holds.
holds.
 :
:
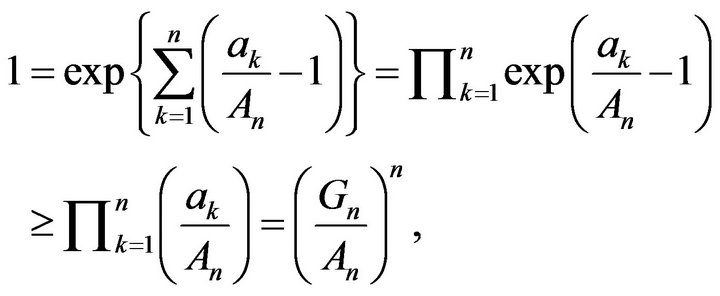
see Bullen ([3], p. 117) or Kuang ([14], p. 33).
 follows by taking
follows by taking .
.
 follows by taking
follows by taking .
.
 : By
: By ,
, . Thus
. Thus . Replacing
. Replacing  by
by , we completes the proof, see Cloud and Dranchman ([6], p. 32).
, we completes the proof, see Cloud and Dranchman ([6], p. 32).
 is clear.
is clear.
 : By
: By ,
, 
Hence, . Thus,
. Thus,  holds, see [3] and [29].
holds, see [3] and [29].
 ,
,  ,
,  and
and  are equivalent, we can also refer to [12].
are equivalent, we can also refer to [12].
 : Without loss of generality, we may assume that
: Without loss of generality, we may assume that  By
By ,
,

Hence

Thus,  holds.
holds.
 : For any x, a > 0, it follows from
: For any x, a > 0, it follows from  that
that . Taking
. Taking , we get
, we get .
.
 see Hardy etc. ([8], pp. 40-41) or Wang, Su, Wang [33].
see Hardy etc. ([8], pp. 40-41) or Wang, Su, Wang [33].
 : Taking
: Taking  in
in ,
, 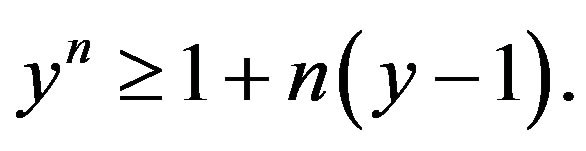
Hence, .
.
 : Taking
: Taking  in
in ,
, 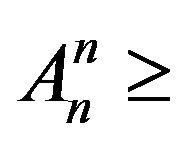
 .
.
Hence,

This completes the proof of , see Bullen ([3], p. 98) or Kuang ([14], p. 33).
, see Bullen ([3], p. 98) or Kuang ([14], p. 33).
 follows by taking ck = 1 for k = 1, 2, ···, n.
follows by taking ck = 1 for k = 1, 2, ···, n.
 : By
: By ,
, .
.
Hence,  is midpoint convex on
is midpoint convex on . Since
. Since  is continuous on
is continuous on ,
,  is a convex function on
is a convex function on . Thus,
. Thus, 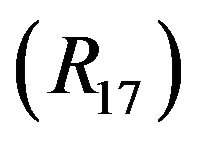 holds.
holds.
We can also prove  by using the mathematical induction.
by using the mathematical induction.
Thus, our proof is complete.
5. Other Equivalent Forms of Bernoulli’s Inequality
In this section, we shall collect some variants of Young’ inequality which is equivalent to the Bernoulli’s inequality.
Theorem 5.1 Let  be positive numbers for
be positive numbers for
 If
If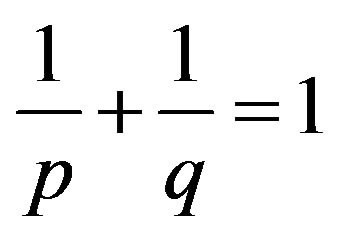 , where the real numbers p, q satisfy
, where the real numbers p, q satisfy ,
,  , then the following some inequalities are equivalent:
, then the following some inequalities are equivalent:








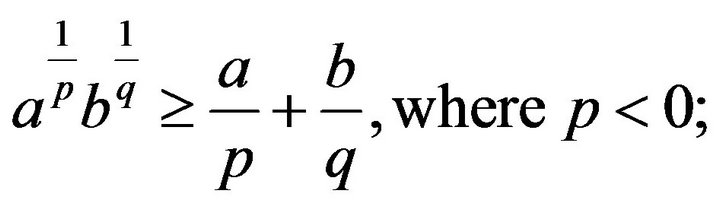





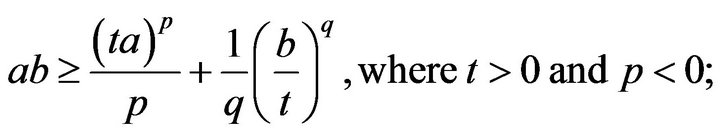

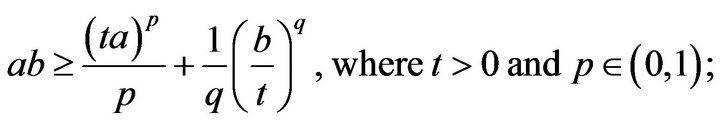








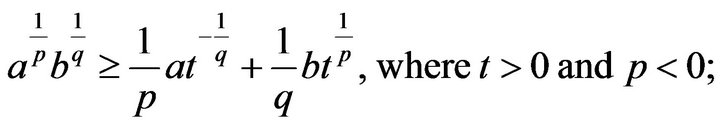





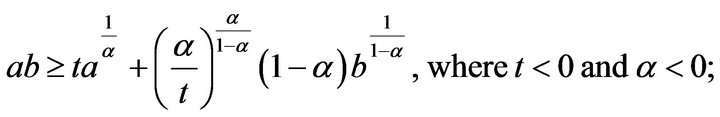



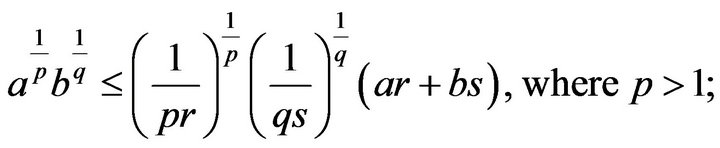
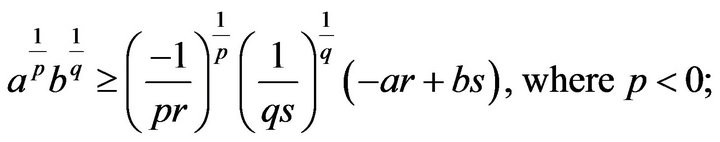








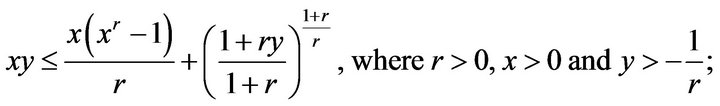
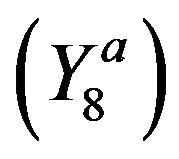

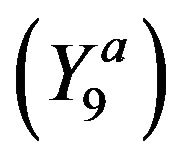


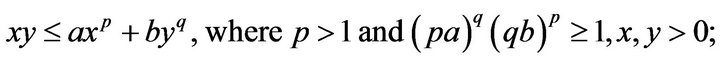


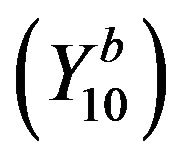











 and there exists exactly one of
and there exists exactly one of  is positive, the other are negative;
is positive, the other are negative;

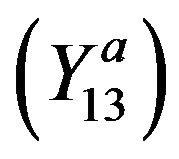 satisfying
satisfying  and
and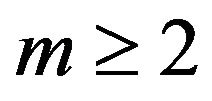 ;
;

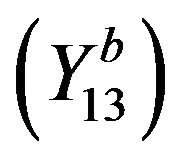 satisfying
satisfying  and
and ;
;
Proof Clearly,  are variant of
are variant of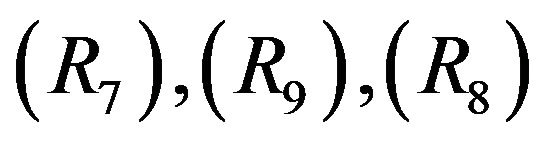 , respectively. Hence
, respectively. Hence  and
and  are equivalent.
are equivalent.
 ,
,  is clear.
is clear.
 : Replacing
: Replacing  by
by  in
in , respectively, we get
, respectively, we get , where
, where .
.
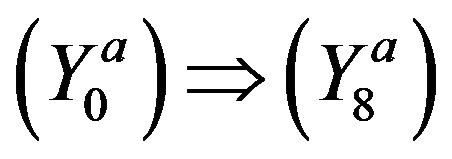 : Let
: Let ,
,  ,
,  , where
, where . Then , by
. Then , by ,
,

Hence

Thus,

This completes our proof.
 : For all
: For all ,
, 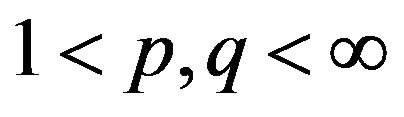 satisfying
satisfying 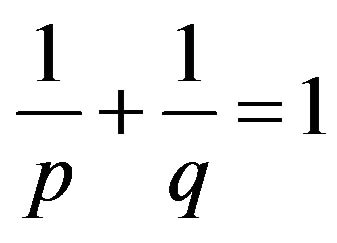 and
and , by
, by ,
,

This prove the proof of .
.
 follows by taking
follows by taking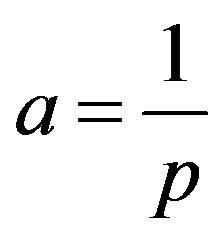 ,
,  in
in .
.
 and
and , see also Sun [31].
, see also Sun [31].
 : Let
: Let ,
,  satisfy
satisfy . Then, for
. Then, for ,
,

Thus, 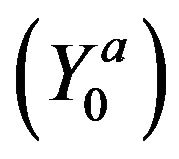 holds.
holds.
 follows by replacing
follows by replacing  by
by 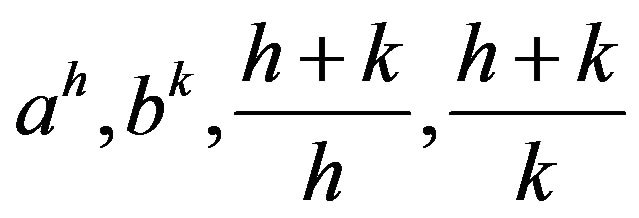 in
in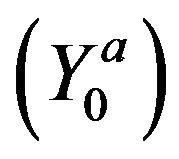 , respectively. Conversely,
, respectively. Conversely,  is clear.
is clear.
Similarly, we can prove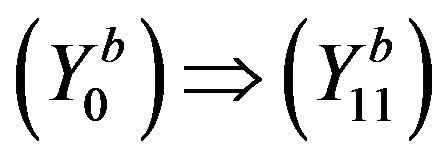 ,
, .
.
 and
and 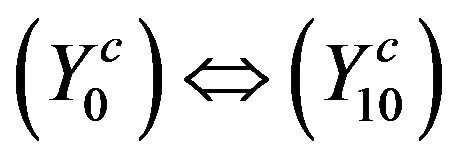 can be proved similarly.
can be proved similarly.
 follows by using the mathematical induction.
follows by using the mathematical induction.
If , then
, then  and
and .
.
 ,
, : Replacing a, b by
: Replacing a, b by  in
in , respectively, we get
, respectively, we get .
.
Similarly,  , where
, where  follows by replacing a, b by
follows by replacing a, b by ,
,  in
in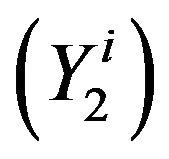 , respectively.
, respectively.
 : Replacing a, b by
: Replacing a, b by  in
in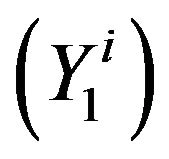 , respectively,
, respectively,  , where
, where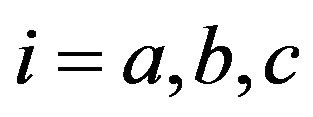 . Similarly, we can prove
. Similarly, we can prove , where
, where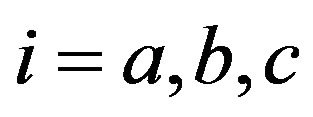 .
.
 : Replacing a, b by
: Replacing a, b by  in
in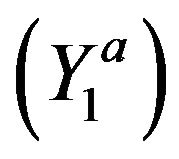 , respectively, we get
, respectively, we get .
.
 : Replacing a, b by
: Replacing a, b by 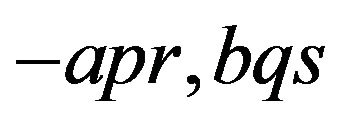 in
in , respectively, we get
, respectively, we get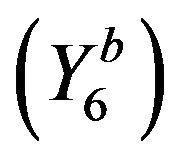 .
.
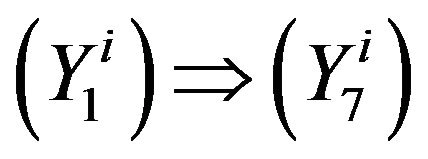 : Replacing a, b by
: Replacing a, b by 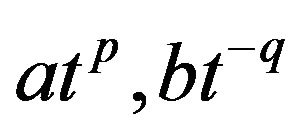 in
in , respectively, we get
, respectively, we get , Similarly, we can prove
, Similarly, we can prove 
 , where
, where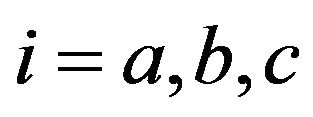 .
.
 : Replacing
: Replacing 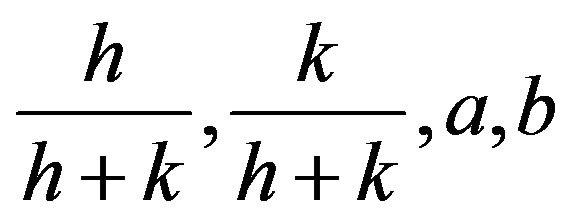 by
by  in
in , respectively, we get
, respectively, we get , where
, where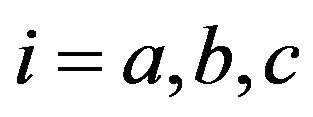 .
.
 : It follows from Theorem 3.1 that
: It follows from Theorem 3.1 that ,
,  and
and  are equivalent. Without loss of generality, we may assume that
are equivalent. Without loss of generality, we may assume that  in
in . Replacing
. Replacing  by
by  in
in , respectively, where
, respectively, where 
 . It follows from
. It follows from 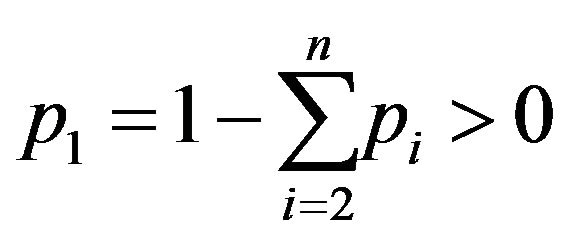 and
and  that
that

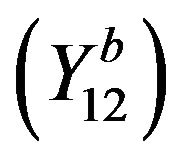 holds.
holds.
 : Replacing
: Replacing  by
by  in
in , we get
, we get , where
, where .
.
 : Replacing
: Replacing  by
by  in
in , respectively, we get
, respectively, we get , where
, where .
.
 : Replacing
: Replacing  by
by  in
in , we get
, we get , where
, where . Similarly, we can prove
. Similarly, we can prove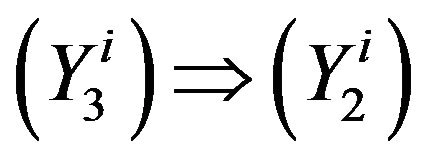 , where
, where .
.
 follows by replacing
follows by replacing  by
by  in
in , respectively.
, respectively.
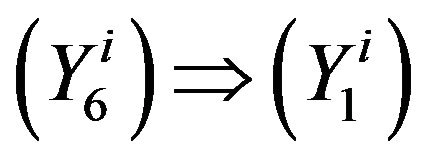 follows by taking by
follows by taking by  in
in , where
, where .
.
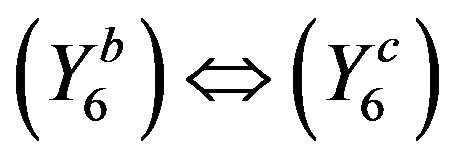 follows by replacing
follows by replacing  by
by , respectively.
, respectively.
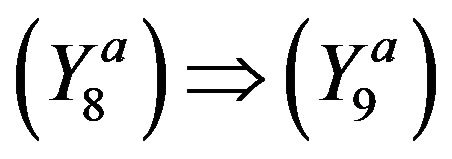 : Since
: Since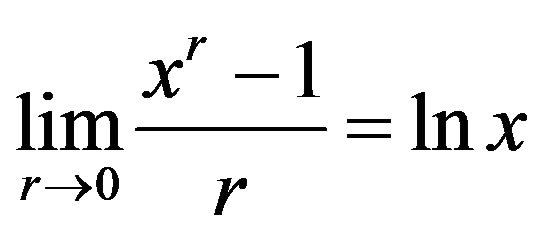 ,
,  therefore, by
therefore, by , we get
, we get .
.
 : Taking
: Taking  in
in , we get
, we get .
.
 : Letting
: Letting  in
in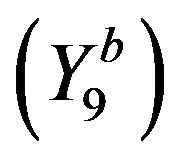 ,
,  And then, by taking
And then, by taking , we get
, we get  This completes the proof of
This completes the proof of .
.
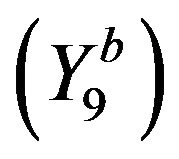 is a variant of
is a variant of .
.
 and
and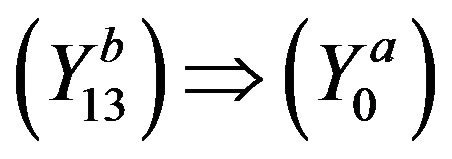 , see Sun [31].
, see Sun [31].
 follows by taking
follows by taking , where
, where .
.
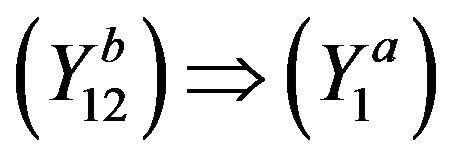 : By Theorem 3.1,
: By Theorem 3.1,  and
and  are equivalent. It suffices to show
are equivalent. It suffices to show . We assume
. We assume  and
and . Replacing
. Replacing  by
by  in
in , respectively, and then, replacing
, respectively, and then, replacing  by
by 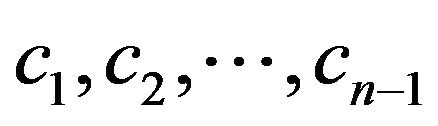 and taking
and taking , it follows from
, it follows from  that
that  holds.
holds.
 : It follows from
: It follows from 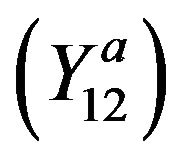 and
and  that
that 
Replacing  by
by , we complete our proof.
, we complete our proof.
Similarly, we can prove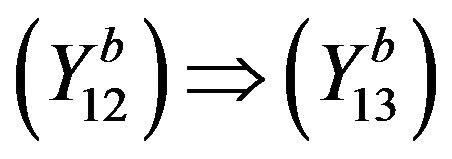 .
.
 and
and  are clear.
are clear.
Remark 5.2 For inequality , we refer to Isumino and Tominaga [13]. For inequality
, we refer to Isumino and Tominaga [13]. For inequality , we refer to [3].
, we refer to [3].
For inequality  and
and , we refer to Sun [31].
, we refer to Sun [31].
For inequality  and
and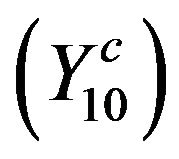 , we refer to Kuang
, we refer to Kuang
[14]. For inequality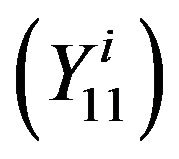 ,
,  , we refer to [34].
, we refer to [34].
For inequality , we refer to Sun [31].
, we refer to Sun [31].
Remark 5.3 There are many variants of Hölder’s inequality, Schlömich’s inequality, AGM inequality, Minkowski’s inequality, and so on, we omit the detail.
NOTES