Study for System of Nonlinear Differential Equations with Riemann-Liouville Fractional Derivative ()
1. Introduction
Let 
denote the 
matrix over real fields 
or complex fields
. For 
here 
is the usual space of continuous functions on 
which is a Banach space with the norm
The space 
is defined by
(see [1]).
The existence of solution of initial value problems for fractional order differential equations have been studied in many literatures such as [1-4]. In this paper, we present the analysis of the system of fractional differential equations
(*)
where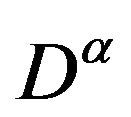 
denotes standard Riemann-Liouville fractional derivative, where
and 
is a square.
To prove the main result, we begin with some definitions and lemmas. For details, see [1-5].
Definition 1.1 Let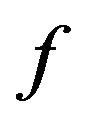 
be a continuous function defined on 
and
. Then the expression
is called left-sided fractional derivatives of order 
Definition 1.2 Let 
be a continuous function defined on 
and 
Then the expression
is called left-sided fractional integral of order 
Lemma 1.3 Given 
with eigenvalues
in any prescribed order, there is a unitary matrix 
such that 
is upper triangular with diagonal entries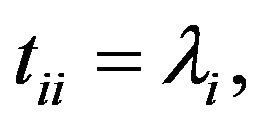 
That is, every square matrix 
is unitarily equivalent to triangular matrix whose entries are the eigenvalues of 
in a prescribed order. Further more, if 
and if all the eigenvalues of 
are real, then 
may be chosen to be real and orthogonal.
Lemma 1.4 Assume that 
with fractional derivative of order 
that belongs to
. Then
for some 
When the function 
then
where
and 
Lemma 1.5 (Schauder’s fixed theorem) Assume 
is a relative subset of a convex set 
in a normed space 
Let 
be a compact map with
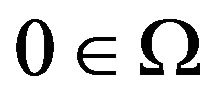. Then either
(A1) 
has a fixed point in
, or
(A2) there is a 
and a 
such that 
Now, let’s us give some hypotheses:
H1: 
is continuous on 
and is such that
(1)
where 
is a continuous function on 
H2: 
is continuous on 
and is such that
(2)
where 
is a continuous function on 
Lemma 1.6 Let 
If we assume that 
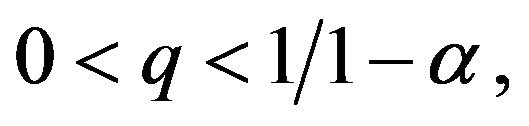then the initial value problem
(3)
where
has at least a solution 
for 
sufficiently small.
Proof. If
then
, by Lemma 1.4, We are therefore reduced the initial problem to the nonlinear integral equation
(4)
The existence of a solution to Problem (3) can be formulated as a fixed point equation 
where
(5)
in the space
.
Define
Clearly, it is closed, convex and nonempty.
Step I. We shall prove that we note that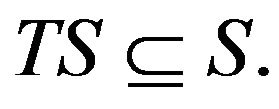 
We note that
Since 
it will be sufficient to impose
In view of the assumption 
the second estimate is satisfied if say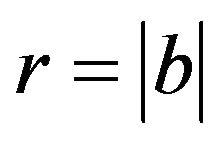 
and 
is chosen sufficiently small.
Step II. We shall prove that the operator 
is compact. To prove the compactness of
defined by (5), it will be sufficient to argue on the operator
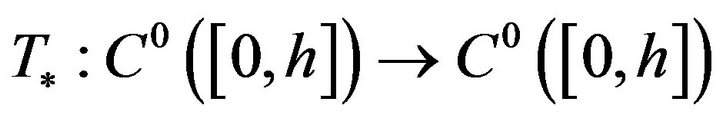
defined in this way:
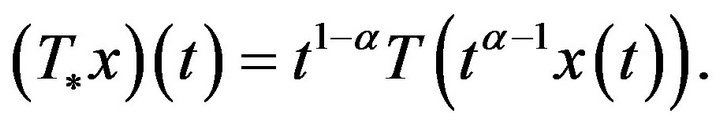
We have 
where the operator
Turn out to be compact from classical sufficient conditions, since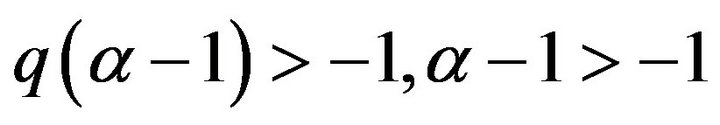
. By Lemma 1.5, we have that Problem (3) has least a solution.
The proof is complete.
Lemma 1.7 Suppose that 
satisfies H1,
and 
If 
for some 
then the problem
(6)
exists a positive constant 
such that 
Lemma 1.8 Let 
with 
Suppose further that
. Then Problem (6) and its associated integral equation
(7)
are equivalent.
Lemma 1.9 Assume that 
satisfies H2, and 
for some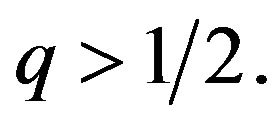 
Suppose further that 
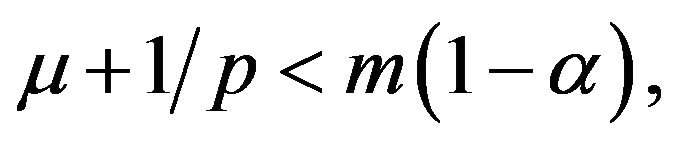then there exists 
and 
such that any solution of (6) exists globally and satisfies
(8)
2. Main Results
Theorem 2.1 Let 
then initial problem (*) has a solution 
where
for all 
and sufficiently small 
Proof. Given 
with eigenvalues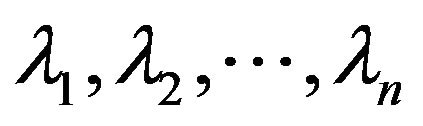 
by Lemma 1.3, there is a unitary matrix 
such that
is upper triangular with diagonal entries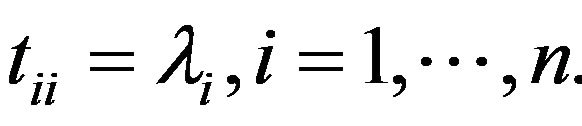 
Let 
we have
At the same time, the initial problem (*) changed into
(**)
Now, let’s consider the problem (**).
Clearly, the problem (**) is equivalent to the following n problems
for 
where 
is the 
th entries of the vector 
Consider the weighed Cauchy-type problem
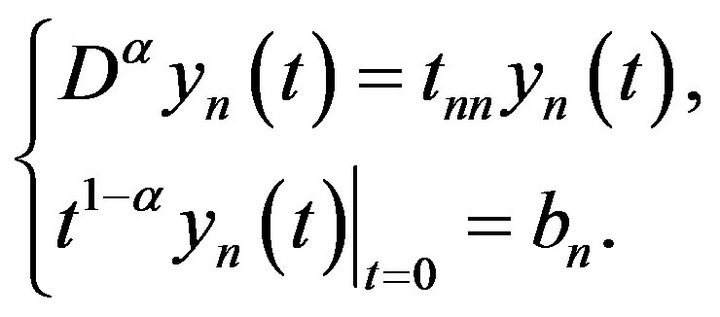
In Lemma 1.6, take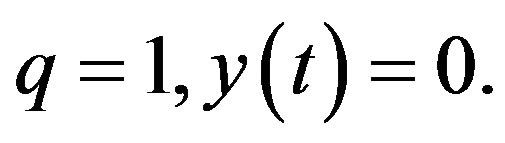 
Then by lemma 1.6, 
s.t. the above problem has at least a solution
Consider the following weighed Cauchy-type problem
In Lemma 1.6, take 
Then by Lemma 1.6,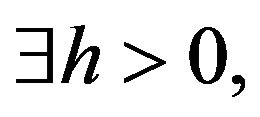 
s.t. the above problem has at least a solution 
Similarly, there has at least a solution in
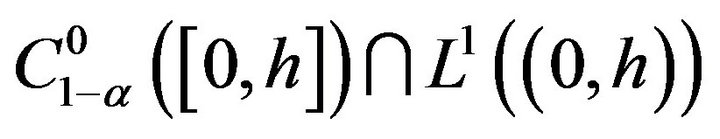
for the rest n-2 initial problem in (**), denote by 
respectively. And therefore, there has at least a solution
of the problem (**). Let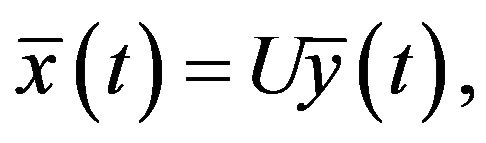 
it is required for us.
The proof is completed.
Since the problem (**) is equivalent to the following n problems
(9)
for 
where 
is the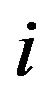 
th entries of the vector 
Next, we shall discuss these equations in (9).
Theorem 2.2 Assume that the right hand of these equations in (9) satisfied H1, 
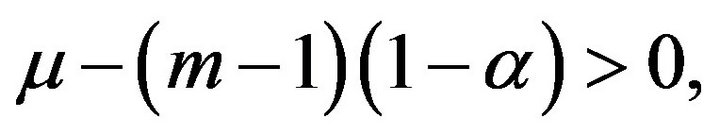and 
for some 
If the solution of the problems (**) denoted by
then there exists some constant 
such that
for all 
Proof. Similar to the proof of Theorem 2.1, now consider the following weighted Cauchy-type problem
Then by Lemma 1.7, there exists some constant 
such that 
Consider the following problem
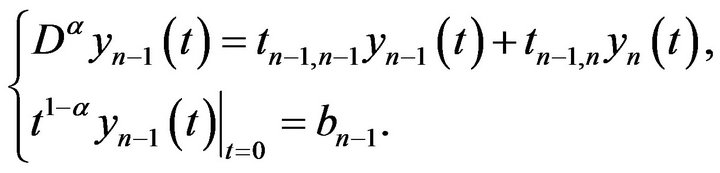
Then by Lemma 1.7, there exists some constant 
such that 
Similarly, there exist some positive constants 
such that
for all 
Let 
Then we have
for all 
The proof is completed.
Theorem 2.3 Assume that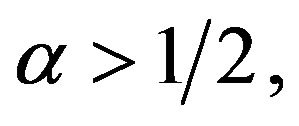 
the right-hand of these equations in (9) satisfied H2, and 
For some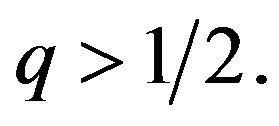 
Suppose further that
If denote solution of the problems (**)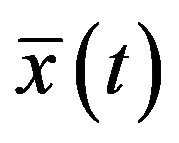
by
Then there exists some constant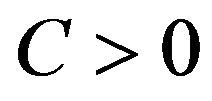 
and
, such that
for all 
Using Lemmas 1.3 and 1.9, the proof is similar to Theorem 2.2. Therefore, it is omitted.
3. Acknowledgements
This research was supported by the NNSF of China (10961020), the Science Foundation of Qinghai Province of China (2012-Z-910) and the University Natural Science Research Develop Foundation of Shanxi Province of China (20111021).
NOTES