Second Descendible Self-Mapping with Closed Periodic Points Set ()
1. Introduction
In this paper, let  denote
denote , X denote compact metric space,
, X denote compact metric space,  denote all continuous self-maps on X. The concepts of periodic point, w-limit point of z and the orbit of z are showed by [2]. Denote by
denote all continuous self-maps on X. The concepts of periodic point, w-limit point of z and the orbit of z are showed by [2]. Denote by  the sets of periodic points of f, denote by
the sets of periodic points of f, denote by  the w-limit points of z, and denote by
the w-limit points of z, and denote by  the orbit of z. A point
the orbit of z. A point  is said to be recurrent point if for any neighborhood
is said to be recurrent point if for any neighborhood  of x, there exists a positive integer m such that
of x, there exists a positive integer m such that . Let
. Let 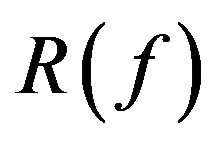 denote the set of recurrent points.
denote the set of recurrent points.
In recent years, many authors studied equivalent conditions of closed periodic points set. Gengrong Zhang [3], Xiong Jincheng [4] and Wang Lidong [5] studied respectively anti-triangular map of X2, continuous self-map of the closed interval and continuous self-map of the circle. They showed equivalent conditions of closed periodic points set (see more detail for [3-5]). Du Ruijin [1] given five equivalent conditions of closed periodic points set if f is a second descendible map of Xn. 1)
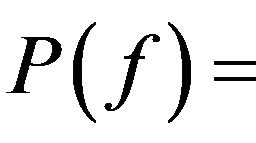 ; 2)
; 2) ; 3)
; 3) ; 4)
; 4)
 ; 5)
; 5)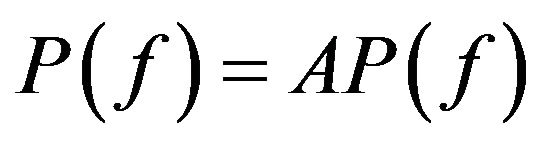 .
.
In this paper, we will continue to study new equivalent conditions about that the set  is closed. The following theorem are given.
is closed. The following theorem are given.
Main Theorem Let  be a continuous map. If f is a second descendible map, then the following properties are equivalent:
be a continuous map. If f is a second descendible map, then the following properties are equivalent:
1) The set  is closed; 2)
is closed; 2)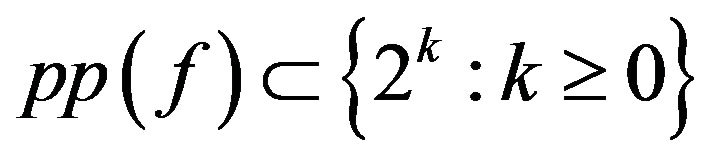 ; 3) For any
; 3) For any , there exists a
, there exists a  such that every point of the set
such that every point of the set  is a isolated point of the set
is a isolated point of the set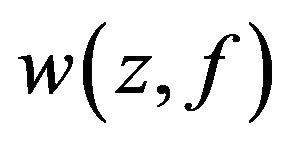 ; 4) For any
; 4) For any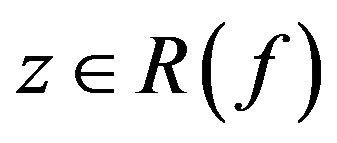 , the set
, the set  is finite; 5) For any
is finite; 5) For any , the set
, the set 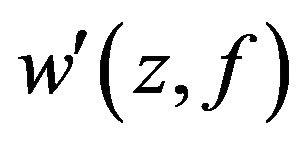 is finite.
is finite.
2. Definition and Lemma
Definition 1 For any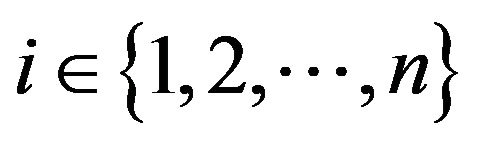 , let
, let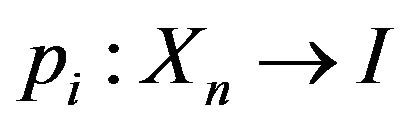 , define:
, define: , then pi is said to be canonical projection.
, then pi is said to be canonical projection.
Definition 2 Let , the map f is said to be second descendible if for any
, the map f is said to be second descendible if for any , there exists
, there exists  such that
such that 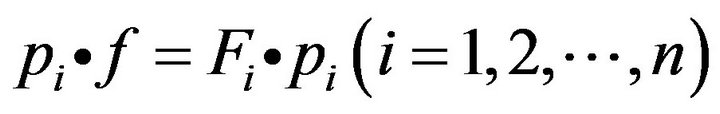 . In this case Fi is a descendible group of f.
. In this case Fi is a descendible group of f.
Lemma 1 [6] Let . Then the following properties are equivalent:
. Then the following properties are equivalent:
1)  is a descendible group of f;
is a descendible group of f;
2) .
.
Lemma 2 Let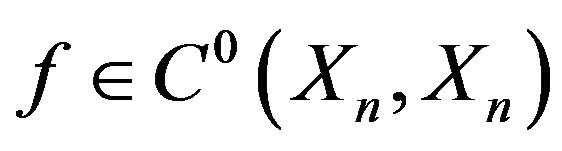 . If f is a second descendible map and
. If f is a second descendible map and  is a descendible group of f, then any
is a descendible group of f, then any , we have
, we have
 .
.
Proof. Suppose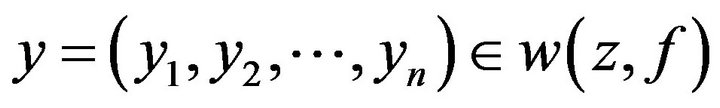 . There exists a positive integer sequence
. There exists a positive integer sequence  such that
such that . By Lemma 1, we can get
. By Lemma 1, we can get
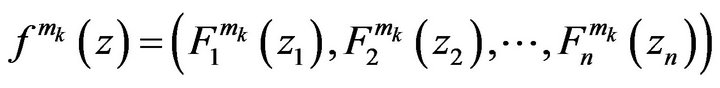 . Hence for any
. Hence for any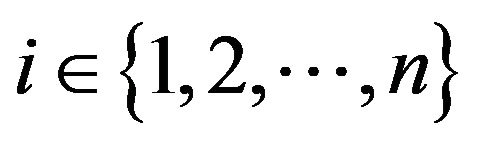 , we have
, we have . Thus
. Thus
 . This complete the proof.
. This complete the proof.
Lemma 3 Let . Then
. Then  if and only if
if and only if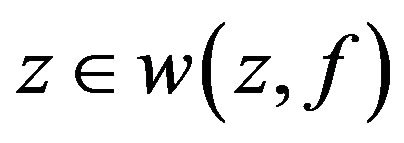 .
.
Proof. Suppose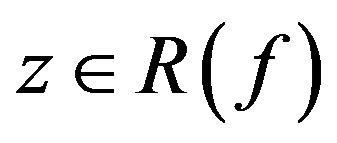 . For any positive integer k, there exists a positive integer sequence
. For any positive integer k, there exists a positive integer sequence  such that
such that
 . Hence
. Hence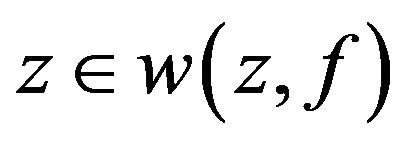 . Assume
. Assume
 . Then there exists a positive integer sequence
. Then there exists a positive integer sequence  such that
such that . By definition,
. By definition,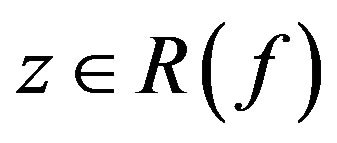 . Hence we complete the proof.
. Hence we complete the proof.
Lemma 4 [5] Let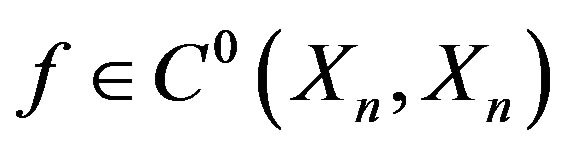 . Then 1) For any
. Then 1) For any , the set
, the set 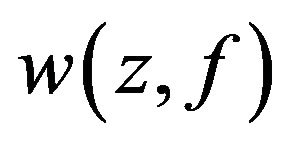 is periodic orbit if and only if the set
is periodic orbit if and only if the set  is finite.
is finite.
2) Let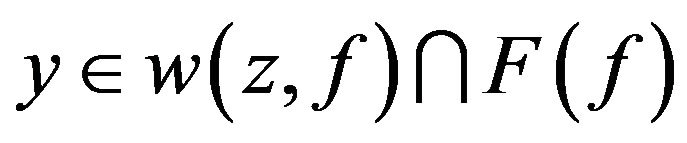 . If y is a isolated point of the set
. If y is a isolated point of the set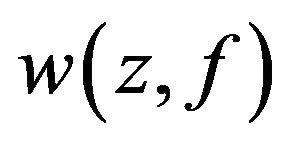 , then we have
, then we have .
.
Lemma 5 Let  and
and 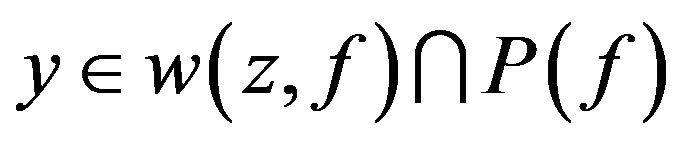 . If all points of the set
. If all points of the set  are isolated points of the set
are isolated points of the set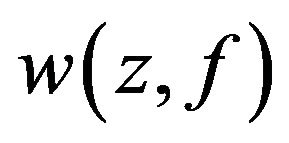 , then we have
, then we have .
.
Proof. Suppose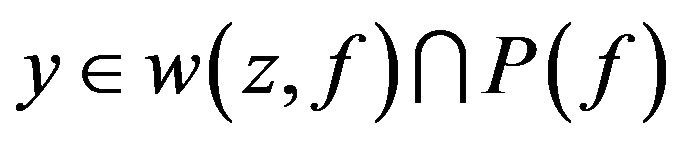 . Then there exists a positive integer l and a sequence
. Then there exists a positive integer l and a sequence  such that
such that  and
and . Hence for any
. Hence for any , we have
, we have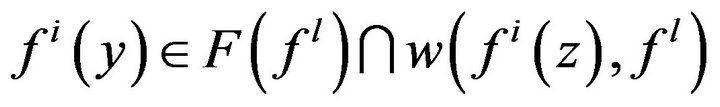 . By assumption, for any
. By assumption, for any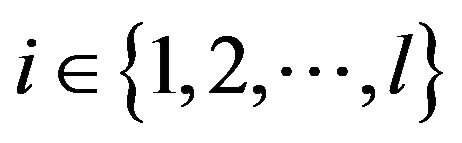 , the point of
, the point of  is a isolated point of the set
is a isolated point of the set . Thus for any
. Thus for any
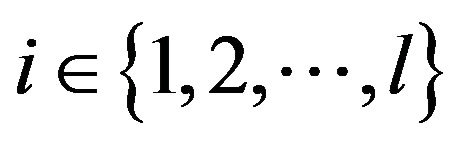 , there exists a neighborhood
, there exists a neighborhood  of
of  such that
such that .
.
Using the equation of , we have
, we have .
.
By 2) of Lemma 4, we can get that 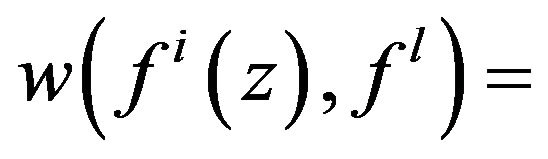
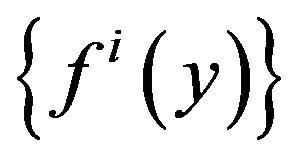 . Hence we have that
. Hence we have that .
.
Lemma 6 Let 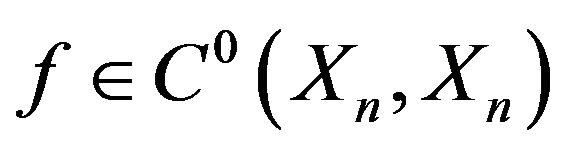 and the set
and the set  is infinite. Then any
is infinite. Then any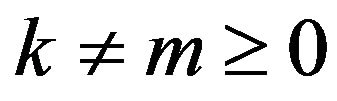 , we can get that
, we can get that  .
.
Proof. Assume on the contrary that there exists  such that
such that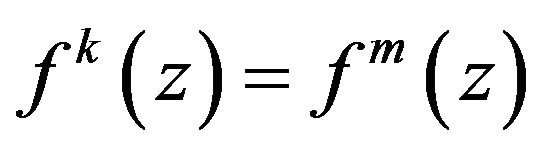 . Thus
. Thus 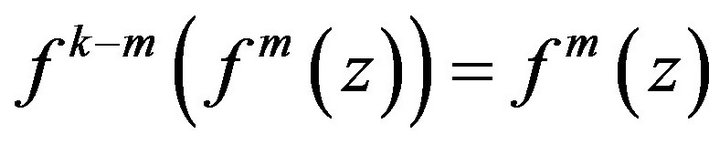 . Hence the point
. Hence the point  is a periodic point. Therefore the set
is a periodic point. Therefore the set  is finite, which is impossible. Thus the lemma is proved.
is finite, which is impossible. Thus the lemma is proved.
Lemma 7 [5] Let  and for any
and for any , the set
, the set  is finite. Then we have
is finite. Then we have .
.
Lemma 8 Let . If f is a second descendible map and
. If f is a second descendible map and  is a descendible group of f, and the set
is a descendible group of f, and the set  is closed. Then any
is closed. Then any  , we have the set
, we have the set  is periodic orbit.
is periodic orbit.
Proof. According to [6], we can get that
 . By assumption, the set
. By assumption, the set  is closed. Hence for any
is closed. Hence for any , the set
, the set  is closed. Let
is closed. Let . According to [4], the set
. According to [4], the set  is closed if and only if for any
is closed if and only if for any , the set
, the set  is periodic orbit. Hence for any
is periodic orbit. Hence for any  and any
and any , the set
, the set  is periodic orbit. Using 1) of Lemma 4, for any
is periodic orbit. Using 1) of Lemma 4, for any  and any
and any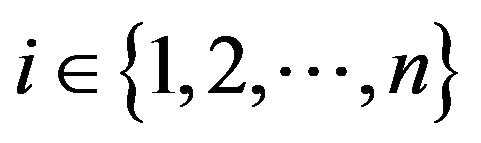 , the set
, the set 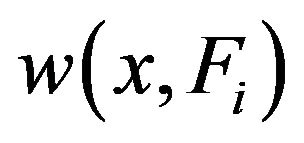 is finite. The set
is finite. The set  is finite since
is finite since . Therefore we have the set
. Therefore we have the set  is periodic orbit.
is periodic orbit.
3. The Proof of Main Theorem
Main Theorem Let  be a continuous map. If f is a second descendible map, then the following properties are equivalent:
be a continuous map. If f is a second descendible map, then the following properties are equivalent:
1) The set  is closed;
is closed;
2) ;
;
3) For any , there exists a
, there exists a 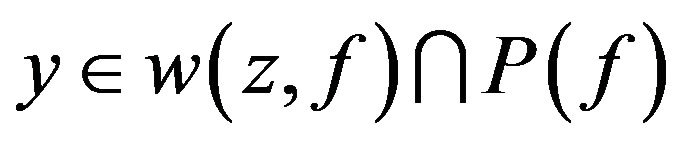 such that every point of the set
such that every point of the set 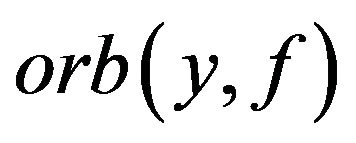 is a isolated point of the set
is a isolated point of the set ;
;
4) For any , the set
, the set  is finite;
is finite;
5) For any , the set
, the set  is finite.
is finite.
Proof. 1)  2) First we will show that the set
2) First we will show that the set  is closed if and only if for any
is closed if and only if for any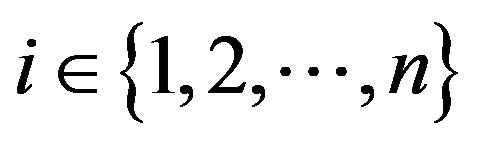 ,
, 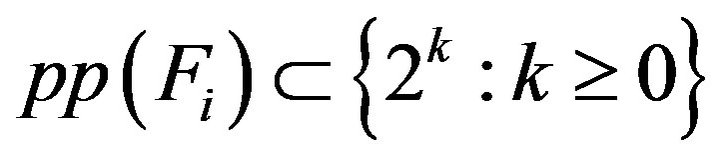 (*).
(*).
According to [6], we can get that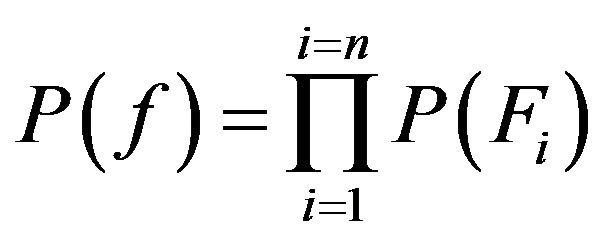 .
.
Hence the set 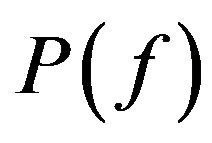 is closed if and only if for any
is closed if and only if for any , the set
, the set  is closed. Let
is closed. Let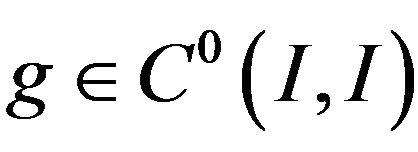 . It is obvious that the set
. It is obvious that the set 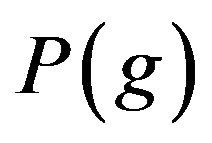 is closed if and only if
is closed if and only if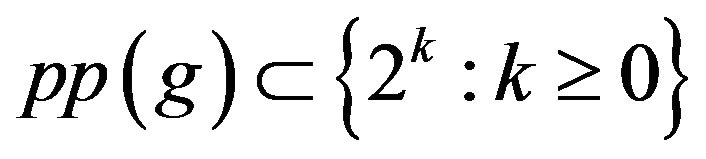 . Thus we complete the proof of (*).
. Thus we complete the proof of (*).
Assume . Then there exists a integer
. Then there exists a integer  such that
such that  for any
for any
 . Hence
. Hence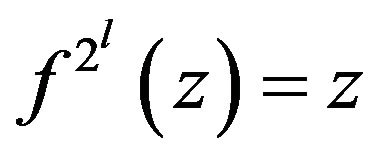 . Therefore 1) implies 2).
. Therefore 1) implies 2).
2)  1) Suppose
1) Suppose . For any
. For any ,
, . Let
. Let . According to [6], we can get that
. According to [6], we can get that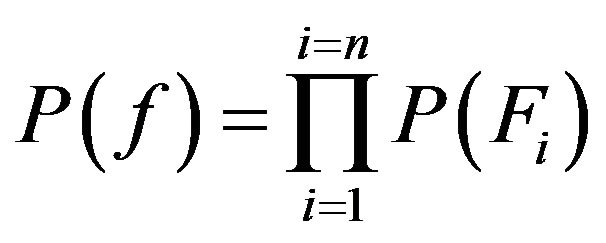 . Hence
. Hence
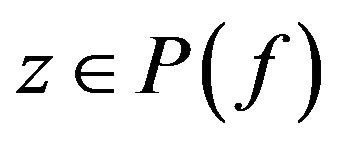 . Then there exists a integer
. Then there exists a integer  such that
such that . Thus for any
. Thus for any . By (*), the set
. By (*), the set  is closed.
is closed.
1)  3) By assumption and according to [1],
3) By assumption and according to [1], . For any
. For any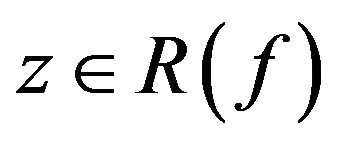 , let
, let . Thus
. Thus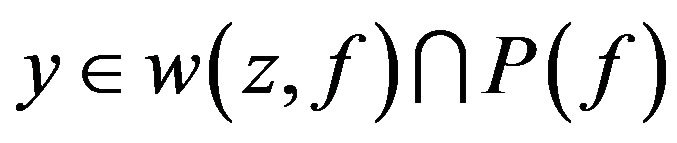 . By assumption and Lemma 8, the set
. By assumption and Lemma 8, the set 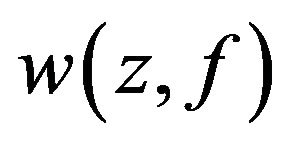 is periodic orbit. Using 1) of Lemma 4, the set
is periodic orbit. Using 1) of Lemma 4, the set 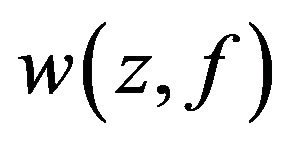 is finite. Hence the set
is finite. Hence the set  is empty. Thus 1) implies 3).
is empty. Thus 1) implies 3).
3)  4) By assumption, for any
4) By assumption, for any , there exists a
, there exists a  such that every point of the set
such that every point of the set  is a isolated point of the set
is a isolated point of the set . By Lemma 5,
. By Lemma 5, . Hence the set
. Hence the set  is finite.
is finite.
4)  5) It is obvious that 4) implies 5).
5) It is obvious that 4) implies 5).
5)  1) For any
1) For any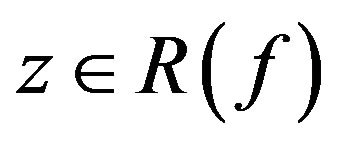 , we have
, we have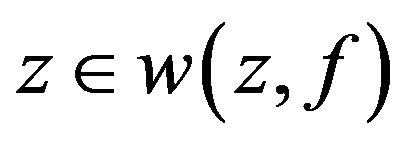 .
.
Case 1: Suppose that the set 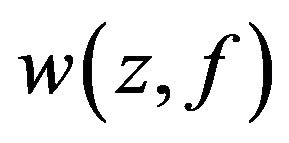 is finite. Using 1) of Lemma 4, the set
is finite. Using 1) of Lemma 4, the set  is periodic orbit. So
is periodic orbit. So . Thus
. Thus .
.
Case 2: Assume that the set  is infinite. Then exists a sequence
is infinite. Then exists a sequence  such that the sequence
such that the sequence 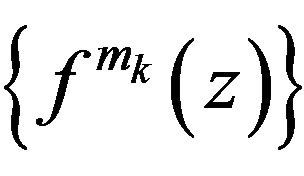 converges to
converges to  and by Lemma 6, all points of the set
and by Lemma 6, all points of the set 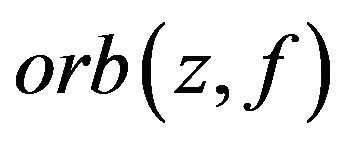 are different. Hence
are different. Hence . By assumption that the set
. By assumption that the set  is finite and Lemma 7, we have that
is finite and Lemma 7, we have that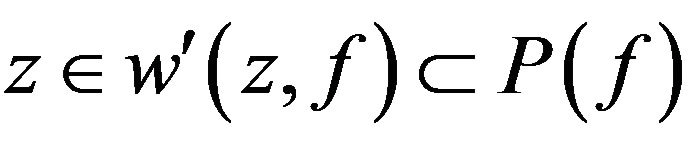 . Thus
. Thus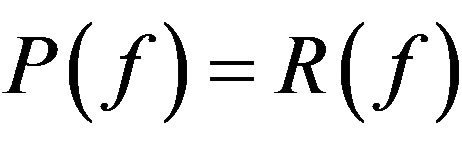 .
.
According to [1], the set 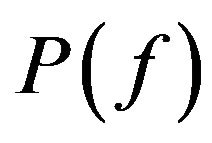 is closed. Thus we complete the proof of the theorem.
is closed. Thus we complete the proof of the theorem.
4. Acknowledgements
This work was supported by the NSF of China (No. 11161029), NSF of Guangxi (2010GXNSFA013109, 2012GXNSFDA276040, 2013GXNSFBA019020).