1. Introduction
In automated theorem proving, resolution is a rule of inference leading to a refutation theorem-proving technique. Applying the resolution rule in a suitable way, it is possible to check whether a propositional formula is satisfiable and construct a proof that a first-order formula is satisfiable/unsatisfiable. In 1965, J. A. Robinson [1] introduced the resolution principle for first-order logic. A resolvent of two clauses  containing the complementary literals
containing the complementary literals  and
and  respectively, is defined as
respectively, is defined as 
 is understood as the disjunction of the literals present in them. It is also a logical consequence of
is understood as the disjunction of the literals present in them. It is also a logical consequence of . A resolution deduction of a clause C from a set
. A resolution deduction of a clause C from a set  of clauses is a finite sequence of clauses
of clauses is a finite sequence of clauses  such that, each
such that, each  is either a member of
is either a member of  or is a resolvent of two clauses taken from
or is a resolvent of two clauses taken from  From the resolution principle in propositional logic we deduce that, if
From the resolution principle in propositional logic we deduce that, if  is true under some truth valuation
is true under some truth valuation , then v(Ci) = TRUE for all i, and in particular,
, then v(Ci) = TRUE for all i, and in particular,  [2].
[2].
Example 1: Here, is a derivation of a clause from a set of clauses presented by means of a resolution Tree in Figure 1.
In first order logic, resolution condenses the traditional syllogism of logical inference down to single rule. To
A simple resoluion scheme is:

recast the logical inference using the resolution technique, first the formulae are represented in conjunctive normal form. In this form, all quantification becomes implicit: universal quantifiers on variables  are simply omitted as understood, while existentially quantified variables are replaced with Skolem functions.
are simply omitted as understood, while existentially quantified variables are replaced with Skolem functions.
The first step in automated deduction in fuzzy logic was taken by Lee and Chang [3]. Lee’s works [3,4] were continued and implemented by many researchers. Lee’s fuzzy formulae are syntactically defined as classical first-order formulae, but they differ semantically as the formulae have a truth value in [0,1]. An interpretation  is defined by an assignment
is defined by an assignment  of a truth value to each atomic formula, from which truth values of compounded formulae are computed [5]. Interpretation
of a truth value to each atomic formula, from which truth values of compounded formulae are computed [5]. Interpretation  is said to satisfy (or falsify) a formula
is said to satisfy (or falsify) a formula , if
, if , the truth value of
, the truth value of  under
under , is at least 0.5 (or at most 0.5). A formula is said to be unsatisfiable if and only if, it is falsified by all its interpretations. A set
, is at least 0.5 (or at most 0.5). A formula is said to be unsatisfiable if and only if, it is falsified by all its interpretations. A set  of clauses is unsatisfiable in fuzzy logic if and only if, it is unsatisfiable in binary logic [3]. Mukaidono [6,7] has generalized Lee’s result in the following way:
of clauses is unsatisfiable in fuzzy logic if and only if, it is unsatisfiable in binary logic [3]. Mukaidono [6,7] has generalized Lee’s result in the following way:
For two clauses  in fuzzy logic, let
in fuzzy logic, let
 where
where  and
and  do not contain the literal
do not contain the literal  and
and  respectively as a factor and have no pair of complementary variables. Then the clause
respectively as a factor and have no pair of complementary variables. Then the clause  is said to be a classical resolvent of
is said to be a classical resolvent of  written as
written as  whose keyword is
whose keyword is  and the contradictory degree of the keyword is
and the contradictory degree of the keyword is . A fuzzy resolvent of
. A fuzzy resolvent of 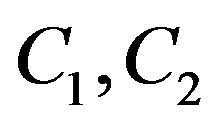 is written as
is written as  where
where  is the contradictory degree of the keyword or the confidence associated with the resolvent. They have computed the truth value of
is the contradictory degree of the keyword or the confidence associated with the resolvent. They have computed the truth value of  from the truth value of
from the truth value of  and the truth values of the atomic formulae. Then, it is proved a set
and the truth values of the atomic formulae. Then, it is proved a set  of fuzzy clauses is unsatisfiable if and only if, there is a deduction of empty clause with its confidence of resolvent
of fuzzy clauses is unsatisfiable if and only if, there is a deduction of empty clause with its confidence of resolvent  from
from  Dubois and Prade [8] established fuzzy resolution principle in the case of uncertain proposition. In [9], antonym-based fuzzy hyper-resolution was introduced and its completeness was proved. S
Dubois and Prade [8] established fuzzy resolution principle in the case of uncertain proposition. In [9], antonym-based fuzzy hyper-resolution was introduced and its completeness was proved. S  nchez et al. [10] proposed a fuzzy temporal constraint logic and introduced a valid resolution principle in order to explain/clarity some queries in this logic. Fontana and Formato [11] introduced a fuzzy resolution rule based on an extended most general unifier supplied by the extended unification algorithm. S. Raha and K. S. Ray [12] presented a generalised resolution principle that handles the inexact situation effectively and is applicable for both well-defined and undefined propositions. They associated a truth value to every proposition. We assume the fuzzy propositions to be completely true and, hence, do not associate partial truth value to the propositions. Our idea is to present, a generalised resolution principle that deals with the fuzzy propositions by the technique of inverse approximate reasoning. The advantage is that, it executes effective resolution and shows its flexibility for automated reasoning. To avoid the generic problem in handling generalised modus ponens (GMP) we use inverse approximate reasoning in fuzzy resolution. We also define fuzzy resolution on the basis of similarity/ dissimilarity measure of fuzzy sets, which is inherent in approximate reasoning.
nchez et al. [10] proposed a fuzzy temporal constraint logic and introduced a valid resolution principle in order to explain/clarity some queries in this logic. Fontana and Formato [11] introduced a fuzzy resolution rule based on an extended most general unifier supplied by the extended unification algorithm. S. Raha and K. S. Ray [12] presented a generalised resolution principle that handles the inexact situation effectively and is applicable for both well-defined and undefined propositions. They associated a truth value to every proposition. We assume the fuzzy propositions to be completely true and, hence, do not associate partial truth value to the propositions. Our idea is to present, a generalised resolution principle that deals with the fuzzy propositions by the technique of inverse approximate reasoning. The advantage is that, it executes effective resolution and shows its flexibility for automated reasoning. To avoid the generic problem in handling generalised modus ponens (GMP) we use inverse approximate reasoning in fuzzy resolution. We also define fuzzy resolution on the basis of similarity/ dissimilarity measure of fuzzy sets, which is inherent in approximate reasoning.
Let us consider two clauses 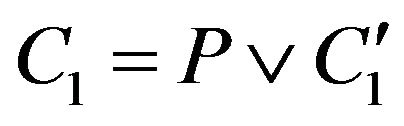 and
and  . Resolvent of
. Resolvent of 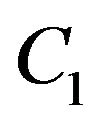 and
and  denoted by
denoted by  if and only if similarity between
if and only if similarity between  and
and  is greater than
is greater than  or equivalently, dissimilarity between
or equivalently, dissimilarity between 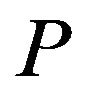 and
and  is less than
is less than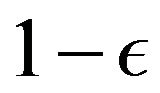 ,
,  being pre-defined threshold. Instead of complementary literal, we introduce similar/dissimilar literal here. The argument form of simple Fuzzy Resolution is as follows.
being pre-defined threshold. Instead of complementary literal, we introduce similar/dissimilar literal here. The argument form of simple Fuzzy Resolution is as follows.

The scheme for Generalised Fuzzy Resolution is given in Table 1.
In this case, we can say that the Disjunctive Syllogism holds if  is close to
is close to 
 is close to
is close to 
The scheme in Inverse Approximate Reasoning looks like as given in the following Table 2.
Here, fuzzy sets  and
and  are defined over the universe of discourse
are defined over the universe of discourse  and fuzzy sets
and fuzzy sets  and
and  are defined over the universe of discourse
are defined over the universe of discourse 
We shall transform the disjunction form of rule into fuzzy implication or fuzzy relation and apply the method of inverse approximate reasoning to get the required resolvent. However, in the case of complex set of clauses the method is not suitable. Hence, we investigate for another method of approximate reasoning based on similarity to get the fuzzy resolvent.
This paper consists of eight sections. In Section 2, we define and dicuss some basic concepts which are used in our paper. We briefly describe two methods of inverse approximate reasoning proposed in [13], in Section 3, and apply the method of inverse approximate reasoning towards fuzzy resolution in Section 4. Another method for fuzzy resolution in the case of complex clauses, is applied in Section 5. Section 6 is devoted with some artificial examples to illustrate the method. At last, in Section 7 some conclusions are made, follwed by some references.
Table 1. Generalised fuzzy resolution.

Table 2. Inverse approximate reasoning.

2. Preliminaries
To study ordinary approximate reasoning as well as inverse approximate reasoning, we have to deal with fuzzy sets, fuzzy relations and operations on fuzzy sets, fuzzy connectives not , and
, and 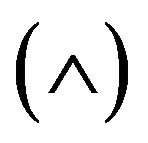 and
and . These are represented by the well known classes of negation functions (to model complement operators), continuous triangular norms (t-norms to model conjunction) and triangular conorms (t-conorms to model disjunction) respectively.
. These are represented by the well known classes of negation functions (to model complement operators), continuous triangular norms (t-norms to model conjunction) and triangular conorms (t-conorms to model disjunction) respectively.
Some well-known t-norms and correlated t-conorms are listed in Table 3, where M, P, B indicate minimum, product, bounded product and drastic product respectively for t-norms, and maximum, algebraic sum and bounded sum respectively, for the correlated t-conorms.
Typically, a fuzzy rule “If  is
is  then
then  is
is ” (
” ( and
and  are fuzzy sets) is expressed as
are fuzzy sets) is expressed as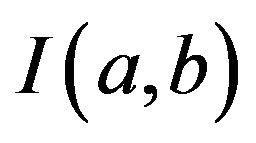 , where
, where  is a fuzzy implication and
is a fuzzy implication and  and
and  are membership grades of
are membership grades of  and
and  respectively. From an algebraic point of view, some implication operators basically identified in [14] are classified with four families
respectively. From an algebraic point of view, some implication operators basically identified in [14] are classified with four families , where
, where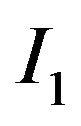 , known as QLimplication, is based on classical logic form
, known as QLimplication, is based on classical logic form  and logical operators are substituted by fuzzy operators. Family
and logical operators are substituted by fuzzy operators. Family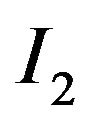 , often named S-implication, derives from classical logic form
, often named S-implication, derives from classical logic form  Families
Families  and
and  reflect a partial ordering on propositions and are based on a generalisation of modus ponens and modus tollens, respectively. Family
reflect a partial ordering on propositions and are based on a generalisation of modus ponens and modus tollens, respectively. Family  is known as R-implication. With reference to the t-norms and t-conorms in Table 3, the explicit expressions of fuzzy implication operators
is known as R-implication. With reference to the t-norms and t-conorms in Table 3, the explicit expressions of fuzzy implication operators  are presented in Table 4.
are presented in Table 4.
Table 3. t-norms and t-conorms.

Table 4. Expression of fuzzy implication operators.

Here, some of the most popular implications such as the Kleene-Dienes, Reichenbach, Lukaseiwicz, Gödel and Gaines implication operators correspond to  respectively.
respectively.
The notion of similarity plays a fundamental role in theories of knowledge and behaviour and has been dealt with extensively in psychology and philosophy. If we study the behaviour pattern of children we find that, children have a natural sense to recognize regularities in the world and to mimic the behavior of competent members of their community. Children thus make decisions on similarity matching. The similarity between two objects suggests, the degree to which properties of one may be inferred from those of the other. The measure of similarity provided, depends mostly on the perceptions of different observers. Emphasis should also be given to different members of the sets, so that no one member can influence the ultimate result. Many measures of similarity have been proposed in the existing literature [15,16]. A careful analysis of the different similarity measures reveals, that it is impossible to single out one particular similarity measure that works well for all purposes.
Suppose U be an arbitrary finite set, and F(U) be the collection of all fuzzy subsets of U. For , a similarity index between the pair {A,B} is denoted as S(A,B;U) or simply S(A,B) which can also be considered as a function S:
, a similarity index between the pair {A,B} is denoted as S(A,B;U) or simply S(A,B) which can also be considered as a function S: . In order to provide a definition for similarity index, a number of factors must be considered. We expect a similarity measure
. In order to provide a definition for similarity index, a number of factors must be considered. We expect a similarity measure  to satisfy the following axioms:
to satisfy the following axioms:
P1. , not A being some negation of
, not A being some negation of .
.
P2. 
P3.  if and only if
if and only if .
.
P4. For two fuzzy sets  and
and , simultaneously not null, if
, simultaneously not null, if  then
then  for all
for all , i.e.,
, i.e., .
.
P5. If either  or
or  then
then  .
.
A similarity measure between two fuzzy sets satisfying these axioms can also be termed as a f-near-degree. For , if
, if , we say that the two fuzzy sets
, we say that the two fuzzy sets  and
and  are
are  -similar. We now consider a definition of measure of similarity which has been proposed in [17,18].
-similar. We now consider a definition of measure of similarity which has been proposed in [17,18].
Definition 1—Similarity Indices: Let  and
and  be two fuzzy sets defined over the same universe of discourse
be two fuzzy sets defined over the same universe of discourse 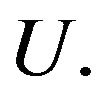 The similarity index
The similarity index  of pair
of pair  is defined by
is defined by

where  is the cardinality of the universe of discourse and
is the cardinality of the universe of discourse and 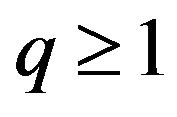 is the family parameter. Here,
is the family parameter. Here,  is a real number such that a large
is a real number such that a large  always gives a large similarity measure. It is left to the user to set
always gives a large similarity measure. It is left to the user to set  for a problem. It is easy to say that the similarity measure referred to in the Definition 1 satisfies axioms P1, P2, P3, P4 and P5.
for a problem. It is easy to say that the similarity measure referred to in the Definition 1 satisfies axioms P1, P2, P3, P4 and P5.
 implies that “
implies that “ is at least as close to
is at least as close to  as
as  is to
is to ”.
”.  as given in Definition 1 is quite sensitive-every change in
as given in Definition 1 is quite sensitive-every change in  or
or  will be reflected in
will be reflected in . Detailed clarification of choice of the definition is described in [18].
. Detailed clarification of choice of the definition is described in [18].
Measure of dissimilarity is another measure of comparison of objects in literature. Many authors like B. Meunier et al. [15] have defined measure of dissimilarity in different way. However, we use the dissimilarity measure in the context of similarity measure and consider measure of dissimilarity of two fuzzy subsets  and
and  defined over
defined over , denoted by
, denoted by  as
as 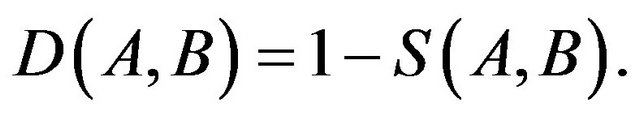 Moreover, we assume
Moreover, we assume  Through out the paper, we use this concept of dissimilarity. In the next section, method of inverse approximate reasoning is discussed briefly.
Through out the paper, we use this concept of dissimilarity. In the next section, method of inverse approximate reasoning is discussed briefly.
3. Inverse Approximate Reasoning
Let there be a fuzzy rule: “If  flow rate is LOW then heating power is LOW”. Let us suppose that the “heating power is rather LOW”. Then, by the method of inverse approximate reasoning with a single rule, we may construct hypotheses which would explain the causes of observation by fuzzy mathematical method. Let us consider a second example as considered in [19]. Let there be two fuzzy rules: “if the traffic is crowded then the flow is low” and “if the visibility is weak then the flow is low”. Suppose, we observe “the flow is very low”. According to these two linguistic rules and the corresponding observation, we first construct hypotheses by abduction such as “the traffic is very crowded” or “the visibility is very weak” or “the traffic is very crowded and the visibility is very weak”. It is difficult to decide which are possible explanations for this observation. N. Mellouli and B. Bouchon-Meunier [20] have used generalised modus ponens (GMP) to construct abductive hypotheses and used the measure of similitude to construct the best possible explanation. Here, we consider a single rule for the method of inverse approximate reasoning.
flow rate is LOW then heating power is LOW”. Let us suppose that the “heating power is rather LOW”. Then, by the method of inverse approximate reasoning with a single rule, we may construct hypotheses which would explain the causes of observation by fuzzy mathematical method. Let us consider a second example as considered in [19]. Let there be two fuzzy rules: “if the traffic is crowded then the flow is low” and “if the visibility is weak then the flow is low”. Suppose, we observe “the flow is very low”. According to these two linguistic rules and the corresponding observation, we first construct hypotheses by abduction such as “the traffic is very crowded” or “the visibility is very weak” or “the traffic is very crowded and the visibility is very weak”. It is difficult to decide which are possible explanations for this observation. N. Mellouli and B. Bouchon-Meunier [20] have used generalised modus ponens (GMP) to construct abductive hypotheses and used the measure of similitude to construct the best possible explanation. Here, we consider a single rule for the method of inverse approximate reasoning.
Definition 2—Inverse Approximate Reasoning: Let
 (1)
(1)
be a given rule, where  and
and  are fuzzy subsets defined over the universes of discourse
are fuzzy subsets defined over the universes of discourse  and
and  respectively. From a given fact “
respectively. From a given fact “ is
is ”, where
”, where 
is a fuzzy subset of 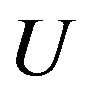 we can conclude that “
we can conclude that “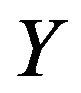 is
is ”, where
”, where 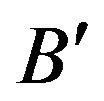 is a fuzzy subset of
is a fuzzy subset of , by applying some method of approximate reasoning. This is called forward approximate reasoning. Now for given “
, by applying some method of approximate reasoning. This is called forward approximate reasoning. Now for given “ is
is ”, we consider
”, we consider 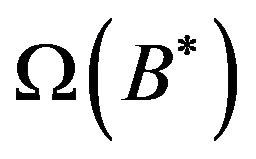 be the set of all fuzzy subsets
be the set of all fuzzy subsets  of
of  such that for given “
such that for given “ is
is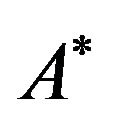 ” we can conclude “
” we can conclude “ is
is ” by the method of approximate reasoning. We have to choose the best member/s of
” by the method of approximate reasoning. We have to choose the best member/s of 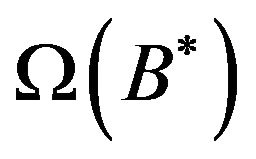 (not empty) in some sense and define some inverse mapping from fuzzy subsets of
(not empty) in some sense and define some inverse mapping from fuzzy subsets of 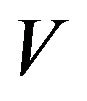 into fuzzy subsets of
into fuzzy subsets of , which we refer here as inverse approximate reasoning. We shall discuss briefly two methods of inverse approximate reasoning presented in [13] to establish fuzzy resolution principle.
, which we refer here as inverse approximate reasoning. We shall discuss briefly two methods of inverse approximate reasoning presented in [13] to establish fuzzy resolution principle.
3.1. Similarity Based Inverse Approximate Reasoning
Our aim, in [13], was to feed the method of similaritybased approximate reasoning [17] to inverse approximate reasoning by writing the rule into its equivalent form. Let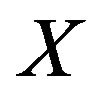 ,
,  be two linguistic variables and
be two linguistic variables and ,
,  be their respective universes of discourse. Two typical propositions “p” and “q” are given in scheme as presented in Table 2 and we may derive a conclusion according to similarity based inference method [17] of the scheme in Table 2. The membership values of
be their respective universes of discourse. Two typical propositions “p” and “q” are given in scheme as presented in Table 2 and we may derive a conclusion according to similarity based inference method [17] of the scheme in Table 2. The membership values of  and
and 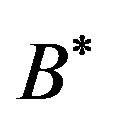 are defined as before. Unlike the existing similarity based methods, a convenient way to represent a rule given by premise “p” is in the form of a fuzzy relation. The rule in premise “p” may be transformed into its equivalent form “
are defined as before. Unlike the existing similarity based methods, a convenient way to represent a rule given by premise “p” is in the form of a fuzzy relation. The rule in premise “p” may be transformed into its equivalent form “ ” of the given premise “p”. We represent this equivalent rule by a fuzzy relation
” of the given premise “p”. We represent this equivalent rule by a fuzzy relation  [21]. Usually,
[21]. Usually,  is defined on the basis of one of the operation
is defined on the basis of one of the operation , where
, where  is associative, commutative and the conjunction operator in the GL-monoid
is associative, commutative and the conjunction operator in the GL-monoid .
. is the residuation operation associated with the conjunction
is the residuation operation associated with the conjunction 
 and can be viewed as the valuation function for the implication;
and can be viewed as the valuation function for the implication; 
 is an alternative to the lattice operation
is an alternative to the lattice operation  (in this case simply the “min” operation) for the valuation of the conjunction. Then for a given fact, the similarity between the fact and the antecedent of the equivalent form of the given rule denoted by “p” is computed and is used to modify the relation
(in this case simply the “min” operation) for the valuation of the conjunction. Then for a given fact, the similarity between the fact and the antecedent of the equivalent form of the given rule denoted by “p” is computed and is used to modify the relation . Here, every change in the concept, as it appears in the conditional equivalent premise and in the fact, is incorporated into the induced fuzzy relation (say,
. Here, every change in the concept, as it appears in the conditional equivalent premise and in the fact, is incorporated into the induced fuzzy relation (say, ). The conclusion may then be drawn using the projection operation, valuating the existential quantifier by the supremum and the conjunction by the operation
). The conclusion may then be drawn using the projection operation, valuating the existential quantifier by the supremum and the conjunction by the operation . We obtain the definition of the composition of a fuzzy relation and a fuzzy set as
. We obtain the definition of the composition of a fuzzy relation and a fuzzy set as

In order to avoid the use of rule-misfiring, we modify the inference scheme in such a way that significant change will make the conclusion less specific. This is done by choosing an expansion type of inference scheme. Here, the “UNKNOWN” case, i.e., the fuzzy set , is to be taken as the limit of non-specificity. Explicitly, when the similarity value becomes low, i.e., when
, is to be taken as the limit of non-specificity. Explicitly, when the similarity value becomes low, i.e., when  and
and  differ significantly, the inference should be
differ significantly, the inference should be  As for
As for , we expect that
, we expect that  and for all other
and for all other , the relation
, the relation  holds. This in turn implies that, nothing better than what the rule says, should be allowed as a valid conclusion. In view of the above observation we propose a scheme for computation of
holds. This in turn implies that, nothing better than what the rule says, should be allowed as a valid conclusion. In view of the above observation we propose a scheme for computation of  in the following algorithm.
in the following algorithm.
ALGORITHM-SIAR:
Step 1. Translate given premise  and compute
and compute  using some suitable translating rule (possibly, a t-norm).
using some suitable translating rule (possibly, a t-norm).
Step 2. Compute similarity measure  using some suitable definition .
using some suitable definition .
Step 3. Modify  with
with  to obtain the modified conditional relation
to obtain the modified conditional relation  using some scheme C.
using some scheme C.
Step 4. Use sup-projection operation on  to obtain
to obtain  as
as
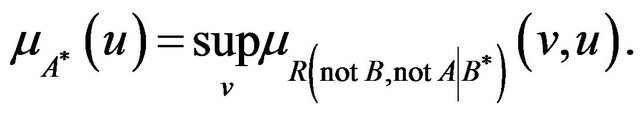 (2)
(2)
In [17,18], authors have proposed two schemes for computation of the modified conditional relation  as given in Step 3, the general form of which is given by:
as given in Step 3, the general form of which is given by:
Scheme C:

where  is any implication function. As previously done in [13], We have
is any implication function. As previously done in [13], We have
 (3)
(3)
and when the conditional relation is interpreted as a t-norm we get

Otherwise, 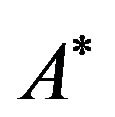 by SIAR could be anything. From (2) and (3) it is found that when
by SIAR could be anything. From (2) and (3) it is found that when 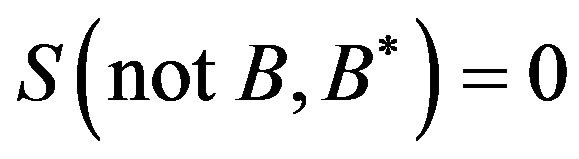 we have
we have  In other words, it is impossible to conclude anything when
In other words, it is impossible to conclude anything when  are completely dissimilar, i.e.,
are completely dissimilar, i.e.,  are completely similar. When
are completely similar. When  is close to unity,
is close to unity,  is close to
is close to  . Hence, the inferred fuzzy set
. Hence, the inferred fuzzy set  will be close to
will be close to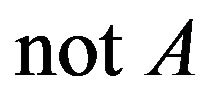 , i.e.,
, i.e., 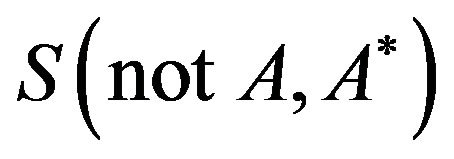 is close to unity. Scheme
is close to unity. Scheme  also ensures that a small change in the input produces a small change in the output and hence, in this sense the above mechanism of inference is reasonable. Let us consider the model as in Table 2 and a theorem is established as follows:
also ensures that a small change in the input produces a small change in the output and hence, in this sense the above mechanism of inference is reasonable. Let us consider the model as in Table 2 and a theorem is established as follows:
Theorem 1: For all 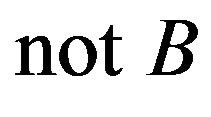 and
and ,
, 
We have investigated another method to deal with fuzzy implication operators in inverse approximate reasoning.
3.2. Method Using Cylindrical Extension and Projection—INAR
We now consider the scheme given in Table 2 and investigate the scheme for generalised modus tollens (GMT). We describe the method simply by an algorithm.
ALGORITHM-INAR:
Step 1. Translate the rule into a fuzzy relation or implication operator .
.
Step 2. Take the  of fuzzy subset
of fuzzy subset  in
in  on
on 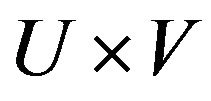 and let it be
and let it be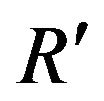 .
.
Step 3. Construct , where
, where  is defined by any fuzzy conjunction operator.
is defined by any fuzzy conjunction operator.
Step 4. Obtain .
.
Symbolically, we get,


 is a t-norm
is a t-norm

by definition of cylindrical extension, which establishes the CRI in the form of GMT. We have to select an appropriate fuzzy implication for the fuzzy relation in Step 1 so as to model GMT. Also the standard negation of the resulted fuzzy set obtained by GMT also gives the given observation by applying GMP. Hence, mathematical formulation of the above algorithm is:
 (4)
(4)
We now deduce some theorems from which we can establish the reasonableness of the method in which negation operator is taken as standard strong negation.
Theorem 2: Let  be normal and
be normal and . Then
. Then , whenever the following implications satisfy the Equation (4) for any t-norm T:
, whenever the following implications satisfy the Equation (4) for any t-norm T:
1) Reichenbach S-implication; 2) Kleene-Dienes S-implication and 3) Lukasiewicz R and S-implication.
Theorem 3: Let  be normal and
be normal and . Then
. Then , whenever both the relation and conjunction in the Equation (4) are defined by any t-norm
, whenever both the relation and conjunction in the Equation (4) are defined by any t-norm .
.
Theorem 4: Let 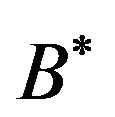 be normal and
be normal and . Then
. Then , whenever the Rescher-Gaines R-implication
, whenever the Rescher-Gaines R-implication  satisfies the Equation (4) for any t-norm T.
satisfies the Equation (4) for any t-norm T.
Theorem 5: Let  be normal and
be normal and . Then
. Then , if
, if 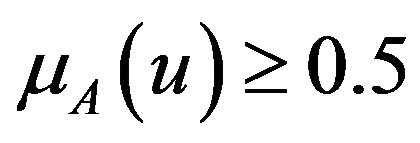 and
and , if
, if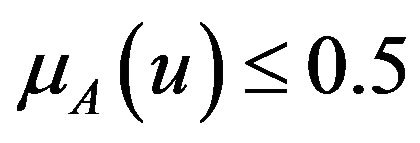 , whenever Gödel R-implication and Gougen R-implication satisfy the Equation (4) for any t-norm T.
, whenever Gödel R-implication and Gougen R-implication satisfy the Equation (4) for any t-norm T.
We observe in the above theorems that if  then either
then either 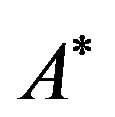 will be
will be 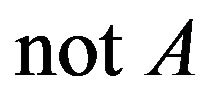 or close to
or close to , that is, we may use GMT in the case of inverse approximate reasoning to get an output in the antecedent part of the given rule and the negation of this output may give
, that is, we may use GMT in the case of inverse approximate reasoning to get an output in the antecedent part of the given rule and the negation of this output may give  by applying GMP. So, we first consider the similarity between
by applying GMP. So, we first consider the similarity between  and
and . If the similarity measure between these two is very very low, i.e.,
. If the similarity measure between these two is very very low, i.e.,  then we expect similarity between
then we expect similarity between  and
and  to be very low, i.e.,
to be very low, i.e.,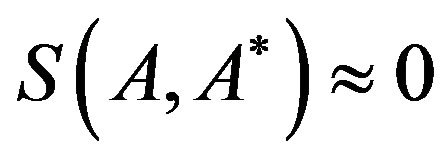 . If the similarity measure between these two is very very high, i.e.,
. If the similarity measure between these two is very very high, i.e.,  then we cannot make any specific conclusion about the similarity between
then we cannot make any specific conclusion about the similarity between  and
and . Therefore, the method of inverse approximate reasoning demands dissimilarity between the specific observation and the consequent of the given rule. So we can apply the method in fuzzy resolution.
. Therefore, the method of inverse approximate reasoning demands dissimilarity between the specific observation and the consequent of the given rule. So we can apply the method in fuzzy resolution.
4. Fuzzy Resolution Based on Inverse Approximate Reasoning
Lately researchers discuss and explore the validity of many classical logic tautologies in fuzzy logic, especially those that involve fuzzy implications. We attempt to exploit such a classical logic equivalence to deal with fuzzy resolution in the framework of inverse approximate reasoning methodology. In classical logic
 (5)
(5)
when extending this classical logic equivalence to fuzzy logic, we interpret the disjunction and negation as a fuzzy union (t-conorm) and a fuzzy complement, respectively. Fuzzy implication thus obtained is usually referred to in the literature as S-implication.
We now consider the classical logic tautology which is obtained from (5).
 (6)
(6)
Therefore, we can extend the classical equivalence (6) into fuzzy logic where fuzzy union is transformed to fuzzy implication.
In fuzzy resolution we deal with the rule of the type “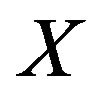 is A or Y is B”. Like classical logic, we may transform the rule into “If
is A or Y is B”. Like classical logic, we may transform the rule into “If  is
is  then
then  is
is ” into fuzzy logic. Then the rule is executed in the method of Inverse Approximate Reasoning described in [13] to obtain the disjunct. The equivalent scheme of Table 1 that conforms fuzzy resolution is given in the Table 5.
” into fuzzy logic. Then the rule is executed in the method of Inverse Approximate Reasoning described in [13] to obtain the disjunct. The equivalent scheme of Table 1 that conforms fuzzy resolution is given in the Table 5.
We have demonstrated earlier in [13] that—if the give data is sufficiently dissimilar to the consequent part of a
Table 5. Equivalent scheme conforms fuzzy resolution.

given rule then one may conclude that the resulting fuzzy set is sufficiently dissimilar to the antecedent part of the rule. Applying this method in the scheme given in Table 5, we get the required resolvent which establishes the fuzzy resolution principle. So the algorithm is as follows.
ALGORITHM-FRIAR:
Step 1. Translate the rule into fuzzy implication as

where  is an implication operator.
is an implication operator.
Step 2. Take cylindrical extension of  in
in  on
on  say
say , defined by
, defined by

Step 3. Construct

where  denotes any fuzzy conjunction operator.
denotes any fuzzy conjunction operator.
Step 4. Obtain  on
on  defined by
defined by

Mathematically, we get
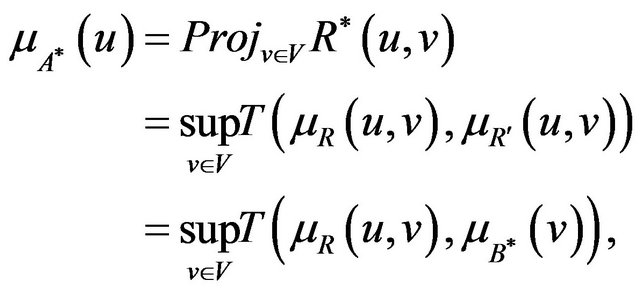 (7)
(7)
where  is a t-norm used to describe fuzzy conjunction operator.
is a t-norm used to describe fuzzy conjunction operator.
It is expected that, for the observation “ is
is ” and the given premise “
” and the given premise “ is
is  or
or  is
is ” we can conclude “
” we can conclude “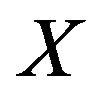 is
is ” by fuzzy resolution. However, for the the observation “
” by fuzzy resolution. However, for the the observation “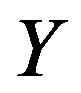 is
is ” no conclusion can be drawn. We establish the above criteria by the following theorems.
” no conclusion can be drawn. We establish the above criteria by the following theorems.
Theorem 6: Let  be normal and
be normal and  be interpreted by any S-implication satisfying Equation (7). Then
be interpreted by any S-implication satisfying Equation (7). Then  for any t-norm
for any t-norm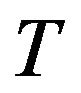 .
.
Proof: We prove the theorem only for Reichenbach S-implication and  Proofs for other implications are same as it.
Proofs for other implications are same as it.




Corollary: Let  be normal and
be normal and  be interpreted by any S-implication satisfying Equation (7). Then
be interpreted by any S-implication satisfying Equation (7). Then  for Lukasiewicz t-norm
for Lukasiewicz t-norm .
.
wang#title3_4:spProof:

Example 2: Consider the premises

in which  and
and  are defined over the universes
are defined over the universes  and
and 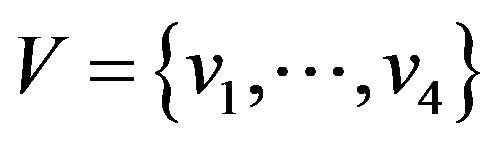 respectively and fuzzy sets labelled by
respectively and fuzzy sets labelled by ,
,  and
and  are defined by
are defined by

The similarity between fuzzy sets  and
and  is
is , i.e., fuzzy set
, i.e., fuzzy set  in observation is dissimilar to fuzzy set
in observation is dissimilar to fuzzy set  in the disjunctive form of rule.
in the disjunctive form of rule.
Again, by INAR, we study the shape of the resolvent  for data given in above with different S-implications and different t-norms, which is described in the Tables 6-8.
for data given in above with different S-implications and different t-norms, which is described in the Tables 6-8.
The result shows that the dissimilarity between 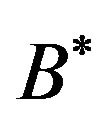 and B assures the similarity between
and B assures the similarity between  and A when the reasoning mechanism is handled using inverse approximate reasoning.
and A when the reasoning mechanism is handled using inverse approximate reasoning.
 “given a disjunction and the negation of one of the disjuncts, the other may be inferred” is established in fuzzy logic.
“given a disjunction and the negation of one of the disjuncts, the other may be inferred” is established in fuzzy logic.
Example 3: Now, we consider the scheme and data of Example 2 except . Consider
. Consider  in Equation (4). We shall observe the results for the given premise “
in Equation (4). We shall observe the results for the given premise “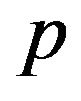 ”and data in Example 2.
”and data in Example 2.
In this case, 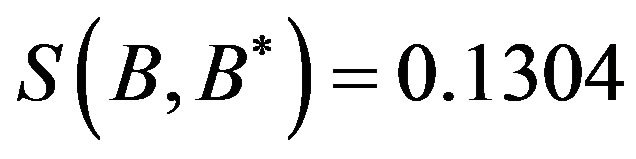 , i.e., fuzzy sets
, i.e., fuzzy sets  and
and  are dissimilar.
are dissimilar.
Table 6. 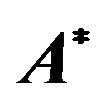 for Reichenbach S-implication.
for Reichenbach S-implication.

Table 7.  for Kleene-Dienes S-implication.
for Kleene-Dienes S-implication.

Table 8.  for Lukasiewicz S-implication.
for Lukasiewicz S-implication.

Let us execute the reasoning mechanism by INAR. The results are shown in Tables 9-11 respectively for different implications and t-norms.
That is, if  is not exactly match with
is not exactly match with  but these are dissimilar, the fuzzy resolvent can be obtained through inverse approximate reasoning method. The technique is very new one.
but these are dissimilar, the fuzzy resolvent can be obtained through inverse approximate reasoning method. The technique is very new one.
Theorem 7: Let 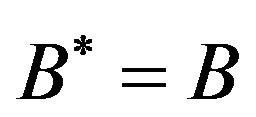 be normal and
be normal and  be interpreted by any implication satisfying Equation (7). Then
be interpreted by any implication satisfying Equation (7). Then  for any t-norm
for any t-norm .
.
wang#title3_4:spProof:

Hence, .
.
We prove the theorem for Reichenbach S-implication and 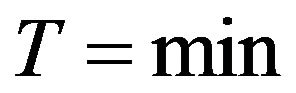 only, but the above theorem can be proved for any other implications and any other t-norms in the similar way.
only, but the above theorem can be proved for any other implications and any other t-norms in the similar way.
Example 4: In Example 2, if we take
 in Equation (4) then either by SIAR or by INAR we get
in Equation (4) then either by SIAR or by INAR we get , for
, for
Table 9. Another  for Reichenbach S-implication.
for Reichenbach S-implication.

Table 10. Another  for Kleene-Dienes S-implication.
for Kleene-Dienes S-implication.

Table 11. Another  for Lukasiewicz S-implication.
for Lukasiewicz S-implication.

all of the cases.
Theorem 8: Let  be normal and
be normal and  be interpreted by Rescher-Gaines R-implication satisfying Equation (7). Then
be interpreted by Rescher-Gaines R-implication satisfying Equation (7). Then  for any t-norm
for any t-norm .
.
Proof:

Example 5: For the data given in Example 2, applying INAR for Recher-Gaines R-implication combined with any t-norm , we get the fuzzy resolvent
, we get the fuzzy resolvent  as
as
 which is a subset of A and
which is a subset of A and 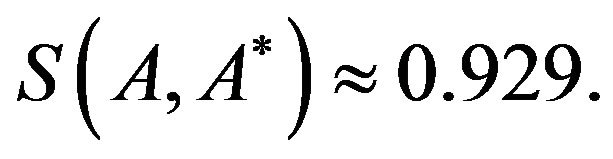 It establishes Theorem 8.
It establishes Theorem 8.
Observation: In Example 2, for another
 , we also get the fuzzy resolvent
, we also get the fuzzy resolvent
 when we apply INAR with Rescher-Gaines R-implication. However, considering other R-implications, except, Lukasiewicz R-implication we cannot get such a fuzzy resolvent
when we apply INAR with Rescher-Gaines R-implication. However, considering other R-implications, except, Lukasiewicz R-implication we cannot get such a fuzzy resolvent  which is a subset of
which is a subset of  for the same input data, although the fuzzy resolvent obtained is significant.
for the same input data, although the fuzzy resolvent obtained is significant.
We are now going to aplpply another method SIAR [13] to obtain fuzzy resolvent for the scheme given in Table 1. Let us consider another classical logic equivalence
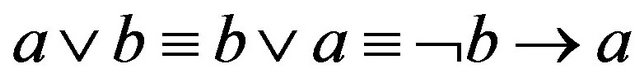 (8)
(8)
The classical logic equivalence (8) can be extended in fuzzy logic with implication and negation function. Then we transform the rule in Table 1 into its equivalent form “ If
If  is
is  then
then  is
is ” over the domain of
” over the domain of . A fuzzy rule may be defined by means of a conjunction for defining a fuzzy Cartesian product rather than in terms of a multivalued logic implication [13,22].
. A fuzzy rule may be defined by means of a conjunction for defining a fuzzy Cartesian product rather than in terms of a multivalued logic implication [13,22].
Therefore, the rule in  is transformed into fuzzy relation
is transformed into fuzzy relation  as
as
 (9)
(9)
where  is a t-norm describing a fuzzy conjunction.
is a t-norm describing a fuzzy conjunction.
Now we can apply our method SIAR described in [13]. The algorithm is as follows:
ALGORITHM-FRSIAR:
Step 1. Translate given premise  and compute
and compute  by Equation (9).
by Equation (9).
Step 2. Compute similarity measure  using some suitable definition .
using some suitable definition .
Step 3. Modify 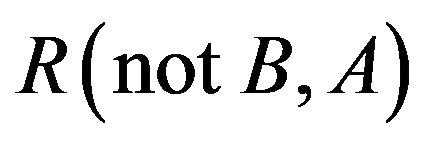 with
with 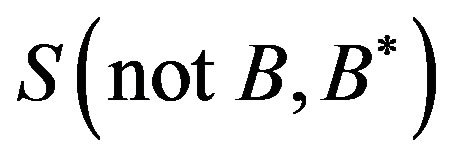 to obtain the modified conditional relation
to obtain the modified conditional relation  using
using  in (3).
in (3).
Step 4. Use sup-projection operation on 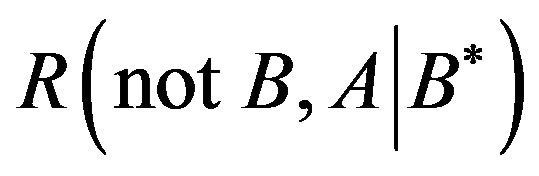 to obtain
to obtain  as
as
 (10)
(10)
We shall illustrate the method applied here by some suitable examples.
Example 6: Let us consider the data in Example 2. For completely dissimilar B* with B and for different t-norms , the shapes of fuzzy resolvent
, the shapes of fuzzy resolvent  in
in  are studied here, when we apply SIAR. The subsequent results are shown in Table 12. In each case, it turns out exacltly the fuzzy set
are studied here, when we apply SIAR. The subsequent results are shown in Table 12. In each case, it turns out exacltly the fuzzy set  which corresponds
which corresponds .
.
Example 7: Consider the data in Example 2 where 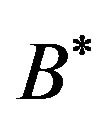 is not completely dissimilar with
is not completely dissimilar with , but dissimilarity exceeds certain threshold. Then, applying SIAR we observe the shapes of
, but dissimilarity exceeds certain threshold. Then, applying SIAR we observe the shapes of  and compare it with given
and compare it with given  for different t-norms, which is shown in Table 13.
for different t-norms, which is shown in Table 13.
Since , i.e.,
, i.e.,  is almost similar to
is almost similar to , it establishes fuzzy resolution in reasoning.
, it establishes fuzzy resolution in reasoning.
In the above methods, we apllied INAR or SIAR when the disjunctive knoledge can be transformed into fuzzy implication. However, it may not always be the case. Moreover, when the expert knowledge is in complex form of disjunction it is difficult to apply INAR or SIAR. So, we extend our method in such a way that can deal with complex premises.
Table 12. Fuzzy resolvent .
.

Table 13.  for another
for another .
.

5. Fuzzy Resolution with Complex Clauses
In this section, we shall extend the scheme given in Table 1. Let ,
,  and
and  be three linguistic variables that take values from the domain U, V and W respectively. We consider the derivation of an inexact conclusion “
be three linguistic variables that take values from the domain U, V and W respectively. We consider the derivation of an inexact conclusion “ ” from two typical knowledge (premises) “
” from two typical knowledge (premises) “ ” and “
” and “ ” acording to the scheme given in Table 14, where
” acording to the scheme given in Table 14, where ’s,
’s, ’s and
’s and ’s are approximations of possibly inexact concepts by fuzzy sets over U, V and W respectively.
’s are approximations of possibly inexact concepts by fuzzy sets over U, V and W respectively.
In 1993, Raha and Ray [12] applied Zadeh’s [23] concept of approximate reasoning with the application of possibility theory to model a deductive process “Generalised Disjunctive Syllogism”. They used projection principle and conjunction principle to deduce fuzzy resolvent. However, the method could not reduce the shortfall of Zadeh’s Compositional rule inference. We have found the shortfalls in [12] as follows:
1) Let fuzzy resolvent be  for
for  in the scheme given in Table 14, by the method of Raha and Ray [12]. The fuzzy resolvent also be same
in the scheme given in Table 14, by the method of Raha and Ray [12]. The fuzzy resolvent also be same  for taking
for taking 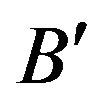 as either
as either  or
or 
2) If we interchange  and
and 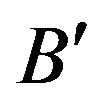 the same fuzzy resolvent
the same fuzzy resolvent  will be produced.
will be produced.
Therefore, firing a rule on the basis of the observation could be harmful. So, it is necessary to modify the relation generated by the two given premises, with the similarity measure of two fuzzy sets involved in the disjunctive form of rules so that the shortfall can be removed. If a pair of fuzzy sets involved having dissimilarity greater than certain pre-defined threshold value, we get our expected fuzzy resolvent using some deductive reasoning. Hence, we investigate another method which is described in the following algorithm.
ALGORITHM-FRCEP:
Step 1. Translate the premise 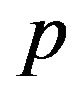 into fuzzy relation
into fuzzy relation

Table 14. Generalised fuzzy resolution—extended form.

as

Step 2. Translate the premise  into fuzzy relation
into fuzzy relation

as

Step 3. Take cylindrical extension of  in
in  on
on 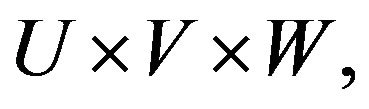 say
say , defined by
, defined by

Step 4. Take cylindrical extension of  in
in 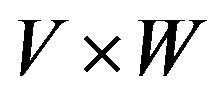 on
on  say
say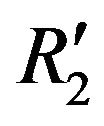 , defined by
, defined by

Step 5. Construct 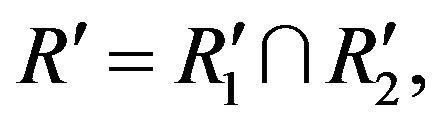 where
where  denotes any fuzzy conjunction operator;
denotes any fuzzy conjunction operator;
Step 6. Compute 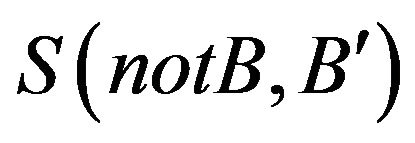 and, say,
and, say,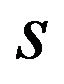 ;
;
Step 7. Modify  with
with  by Scheme
by Scheme  in (3) and, say,
in (3) and, say,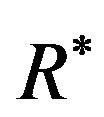 ;
;
Step 8. Obtain  on
on  defined by
defined by

Step 9. Obtain  and
and 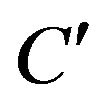 by projecting R separately on U and W such that
by projecting R separately on U and W such that  and
and

Symbolically, the fuzzy resolvent  is obtained by, for
is obtained by, for ,
, 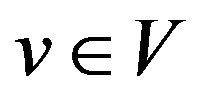 and
and ,
,


This derivation can be achieved if there is a  such that
such that  and
and  which is possible if the fuzzy sets
which is possible if the fuzzy sets  and
and 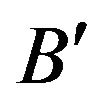 are dissimilar, i.e.,
are dissimilar, i.e.,  and
and  are similar for any implication
are similar for any implication  in derivation. We observe two criteria here.
in derivation. We observe two criteria here.
Criterion 1: Taking  we get
we get

Criterion 2: Taking  we get
we get

From above two criteria we observe that when , i.e., when
, i.e., when  and
and  are completely similar
are completely similar  Therefore, fuzzy resolvent could be anything. However, if
Therefore, fuzzy resolvent could be anything. However, if 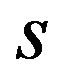 is close to unity, i.e., if
is close to unity, i.e., if  and
and  are almost dissimilar we have
are almost dissimilar we have  is close to
is close to

which, after re-translation, gives “If  is
is  or
or  is
is ”. Again, we observe that a small change in
”. Again, we observe that a small change in  produces a small change in fuzzy resolvent—which ensures our method is resonable one.
produces a small change in fuzzy resolvent—which ensures our method is resonable one.
Let us now investigate another method to find a fuzzy resolvent from a complex set of clauses. It is observed that, to obtain a fuzzy resolvent from two clauses containing a pair of complementary literals defined over the same domain. If the dissimilarity measure of the complementary literals is unity then we get the resolvent by the disjunction of remaining literals and subsequent removal of the complementary literals. The keyword of the fuzzy resolvent is any one of the complementary literals, the degree of confidence of which is measured by the dissimilarity measure of the complementary literals. However, in the case of almost complementary literals for which dissimilarity value does not attain unity, but exceeds a certain pre-defined threshold, we modify the remaining literals with the measure of dissimilarity in such a way that dissimilarity measure of complementary literals tends to unity and we obtain the resolvent by taking the disjunction of modified literals removing the complementary literals. If the dissimilarity measure of a pair of literals is either zero or close to zero, we cannot obtain a fuzzy resolvent. In this way, we can proceed for a method to find out the derivation of the empty clause and establish the refutation method for the proof of a theorem. The degree of confidence of the empty clause is measured by the degree of confidence of keyword that generated the empty clause and, thus, a sort of completeness of fuzzy resolution principle is established.
Let us consider a scheme given in Table 15 where
Table 15. Generalised fuzzy resolution—another extension.

variables  and the respective fuzzy subsets
and the respective fuzzy subsets  are defined on universe
are defined on universe  repectively; variables
repectively; variables  and the respective fuzzy subsets
and the respective fuzzy subsets  are defined on universe
are defined on universe 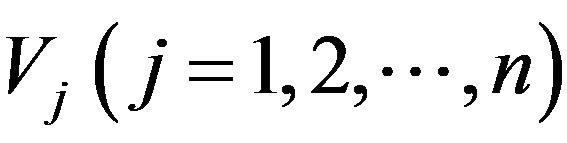 repectively.
repectively. 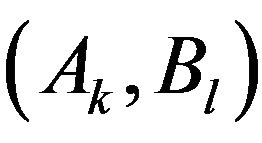 is almost complementary over the same universe
is almost complementary over the same universe  with the degree of confidence of keyword
with the degree of confidence of keyword  is
is  and the corresponding
and the corresponding  are defined over
are defined over 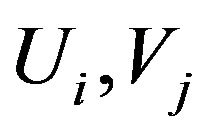 respectively.
respectively.
To show the method we set up an algorithm FRAE as follows:
ALGORITHM-FRAE:
Step 1. Check the domain of pair of literals ,
,  from clauses
from clauses 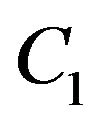 and
and ;
;
Step 2. If the pair remains in the same domain, say,  then measure the dissimilarity of
then measure the dissimilarity of ; Otherwise, there is no fuzzy resolvent;
; Otherwise, there is no fuzzy resolvent;
Step 3. Dissimilarity of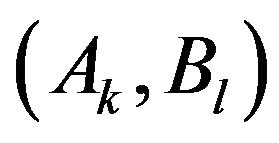 , i.e.,
, i.e.,  is computed by
is computed by 
Step 4. If 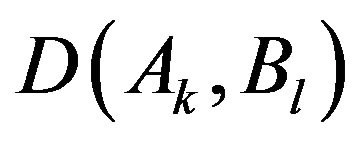 is very very high, i.e.,
is very very high, i.e., 
 is pre-defined threshold then go to the next step and say,
is pre-defined threshold then go to the next step and say,  is keyword; Otherwise, there is no fuzzy resolvent;
is keyword; Otherwise, there is no fuzzy resolvent;
Step 5. Modify Bi either by  or by
or by 
Step 6. Fuzzy resolvent is

and

which is measured as 
Step 7. Repeat the process until empty clause, with the confidence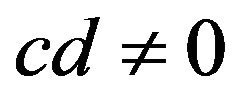 , is derived for more than two clauses.
, is derived for more than two clauses.
Hence, we prove the (un)satisfiability of a theorem by the deduction of empty clause from a set of fuzzy clauses.
6. Artificial Examples
We consider examples to illustrate the models presented in this paper. Let us consider variables that range over finite sets or can be approximated by variables ranging over such sets.
Example 8: Consider the premises

in which ,
,  and
and  are defined over the respective universes
are defined over the respective universes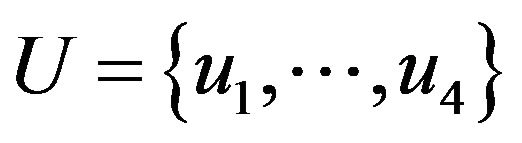 ,
,  and
and  and fuzzy sets labelled by
and fuzzy sets labelled by  ,
,  and
and  are defined by
are defined by

The similarity between fuzzy sets  and
and  is
is , i.e.,
, i.e., . Therefore, in two clauses, fuzzy sets
. Therefore, in two clauses, fuzzy sets  in observation is dissimilar to fuzzy set
in observation is dissimilar to fuzzy set . Hence, we can resolve upon dissimilar pair
. Hence, we can resolve upon dissimilar pair . We apply ALGORITHM-FRCEP to get the resolvent.
. We apply ALGORITHM-FRCEP to get the resolvent.


We construct  where
where  denotes any fuzzy conjunction operator and
denotes any fuzzy conjunction operator and


We modify  with
with 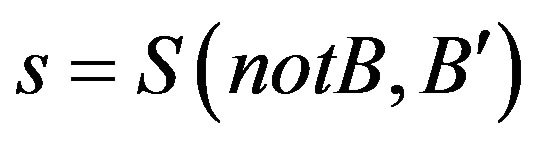 as we get
as we get  (using Scheme
(using Scheme  and
and  in Table 3) and we get
in Table 3) and we get

We can also obtain  and
and  by
by


which are same as  and
and  respectively, since the dissimilarity between
respectively, since the dissimilarity between  and
and  is zero.
is zero.
Again, it is observed that same ,
,  and
and  are obtained for different fuzzy conjunctions (t-norms, here) described in Table 3. However, for different
are obtained for different fuzzy conjunctions (t-norms, here) described in Table 3. However, for different  in premise
in premise , it yields different results.
, it yields different results.
Let us consider 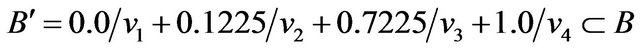 . Similarity between
. Similarity between  and
and  is
is 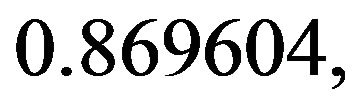 i.e., dissimilarity between
i.e., dissimilarity between  and
and 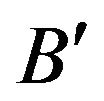 is very low, being less than pre-defined threshold value 0.34(
is very low, being less than pre-defined threshold value 0.34( ). By applying ALGORITHM-FRCEP, we get the fuzzy resolvent as
). By applying ALGORITHM-FRCEP, we get the fuzzy resolvent as

for t-norms M, P and B in Table 3, and by projection we obtain


Similarity between  and
and  is
is  and similarity between
and similarity between  and
and  is
is  which is our expected result.
which is our expected result.
Now, if we consider another  , similarity of which with
, similarity of which with 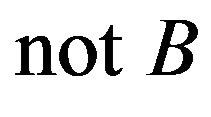 is
is  i.e., dissimilarity of it with
i.e., dissimilarity of it with  is less than
is less than  then, we find the resolvent as
then, we find the resolvent as

for different t-norms in Table 3 and


with  and
and 
Another example can be illustrated whenever number of premises is more than two.
Example 9: Let us consider the premises

where ,
, 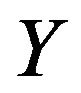 ,
,  and all the fuzzy sets are defined as earlier. Here,
and all the fuzzy sets are defined as earlier. Here,  is defined by
is defined by

Selection of keywords: Since,  in premise p and
in premise p and  in premise q are fuzzy subsets in the same universe U and similarity between
in premise q are fuzzy subsets in the same universe U and similarity between  and
and , i.e.,
, i.e.,  , we resolve upon the keyword
, we resolve upon the keyword , taking the premises p and q together as
, taking the premises p and q together as  and
and  completely dissimilar. Again,
completely dissimilar. Again,  in premise p and
in premise p and  in premise r are fuzzy subsets over the same universe V and
in premise r are fuzzy subsets over the same universe V and . Therefore, after resolving with
. Therefore, after resolving with  and
and  we resolve upon the keyword B with taking
we resolve upon the keyword B with taking 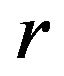 and
and  together. Next, we execute the following steps with the given data, using ALGORITHMFRCEP.
together. Next, we execute the following steps with the given data, using ALGORITHMFRCEP.
Execution:
Step 1: Compute the fuzzy relation  by
by

Step 2: Extend  in U cylindrically on
in U cylindrically on 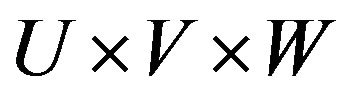 as
as

Step 3: Compute  by
by
 taking fuzzy conjunction
taking fuzzy conjunction  as t-norm
as t-norm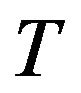 ;
;
Step 4: Modify  with
with 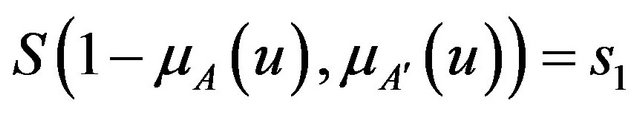 to get
to get 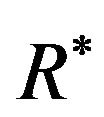 as
as

Step 5: Project  on
on 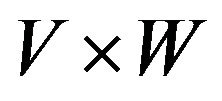 such that
such that

Step 6: Extend  in
in 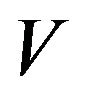 cylindrically on
cylindrically on  as
as

Step 7: Compute 
by
 taking fuzzy conjunction
taking fuzzy conjunction  as t-norm
as t-norm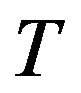 ;
;
Step 8: Modify  with
with 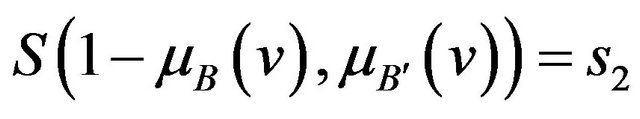 to get
to get  as
as

Step 9: Project  on
on  such that
such that

which is completely similar to , i.e.,
, i.e., .
.
Even if  and
and  in the respective premises
in the respective premises  and
and , are not completely dissimilar to
, are not completely dissimilar to  and
and  respectively, but the dissimilarity measures attain values greater than certain pre-defined threshold then we can get a fuzzy resolvent
respectively, but the dissimilarity measures attain values greater than certain pre-defined threshold then we can get a fuzzy resolvent  which is almost similar to
which is almost similar to , using FRCEP.
, using FRCEP.
Suppose, 

 are computed.
are computed.
Then, it yields

with 
Therefore, it is possible to get a fuzzy resolvent from a set of fuzzy clauses if there is a pair of dissimilar literals contained in the respective clauses.
7. Conclusion
This paper presented a resolution principle for fuzzy formulae based on similarity and approximate reasoning methodology. Similarity is inherent in approximate resoning and resolution deduction can be used as a rule of inference to generate new clause from a given set of clauses. The essential idea of resolution of two clauses is to search for a literal in a clausal formula that is almost complementary to a literal in the other form. The clause formed by the disjunction of the remaining literals and subsequent removal of the pair of almost complementary literals is a logical consequence. If we put the resolvents in the set of clauses its behaviour (satisfiability) never changes. It can be applied directly to any set S of clausal formulae (not necessarily to ground clauses) to test the (un)satisfiability of S. To test the unsatisfiability it checks whether S contains the empty clause (as a resolution deduction). This could be a powerful technique in constructing a proof of a theorem using refutation procedure. Examples cited in the paper attempted to demonstrate how resolution can be effectively used to construct a proof of a theorem. Inverse approximate reasoning may be applied to model different goal-directed search techniques. We apply inverse approximate reasoning method to avoid the inherent problem of GMP. Instead of testing complementary literals we use dissimilarity concept of fuzzy literals.
8. Acknowledgements
This research has been partially supported by the UGC SAP (DRS) Phase-II project under the Department of Mathematics, Visva-Bharati.