Common Fixed Point Result of Multivalued and Singlevalued Mappings in Partially Ordered Metric Space ()
1. Introduction and Preliminaries
Throughout this paper, let  be a metric space unless mentioned otherwise and
be a metric space unless mentioned otherwise and  is the set of all non-empty bounded subsets of
is the set of all non-empty bounded subsets of . Let
. Let  and
and  be the functions defined by
be the functions defined by

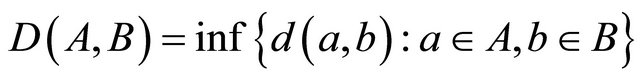
for all A, B in . If A is a singleton i.e.
. If A is a singleton i.e. , we write
, we write

and

If B is also a singleton i.e. , we write
, we write

and

It is obvious that . For all
. For all 
 . The definition of
. The definition of  yields the following:
yields the following:



and
 .
.
Several authors used these concepts of weakly contraction, compatibility, weak compatibility to prove some common fixed point theorems for set valued mappings (see [2-8]).
Definition 1.1. [9] A sequence  of subsets of X is said to be convergent to a subset A of X if 1) Given
of subsets of X is said to be convergent to a subset A of X if 1) Given , there is a sequence
, there is a sequence in X such that
in X such that 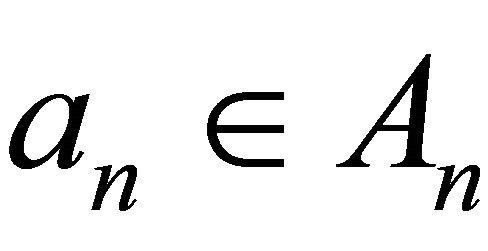 for
for  and
and  converges to a.
converges to a.
2) Given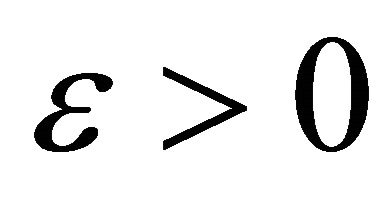 , there exists a positive integer N such that
, there exists a positive integer N such that 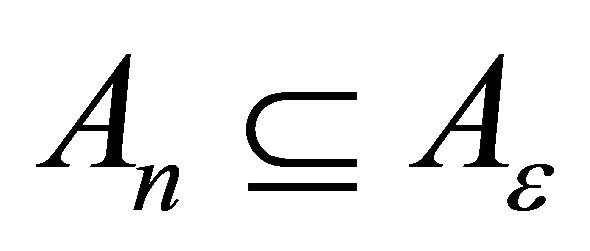 for
for  where
where  is the union of all open spheres with centers in A and radius
is the union of all open spheres with centers in A and radius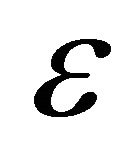 .
.
Lemma 1.1. [9,10] If  and
and  are sequences in
are sequences in  converging to A and B in
converging to A and B in , respectively, then the sequence
, respectively, then the sequence  converges to
converges to .
.
Lemma 1.2. [9] Let  be a sequence in
be a sequence in  and y a point in X such that
and y a point in X such that . Then the sequence
. Then the sequence  converges to the set
converges to the set  in
in .
.
In [11], Jungck and Rhoades extended definition of compatibility to set valued mappings setting as follows:
Definition 1.2. The mapping  and
and  are δ-compatible if
are δ-compatible if  , whenever
, whenever  is a sequence in X such the
is a sequence in X such the  for some
for some .
.
Recently, the following definition is given by Jungck and Rhoades [12].
Definition 1.3. The mapping  and
and  are weakly compatible if for each point u in X such that
are weakly compatible if for each point u in X such that , we have
, we have .
.
It can be seen that any δ-compatible mappings are weakly compatible but the converse is not true as shown by an example in [13]. We will use the following relation between two nonempty subsets of a partially ordered set.
Definition 1.4. [3] Let A and B be two nonempty subsets of a partially ordered set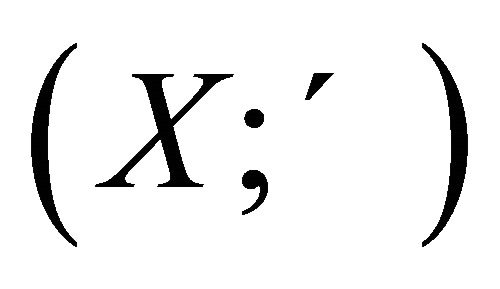 . The relation between A and B is denoted and defined as follows:
. The relation between A and B is denoted and defined as follows: , if for every
, if for every  there exists
there exists  such that
such that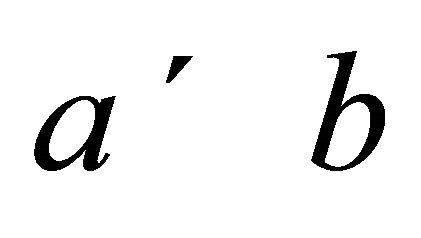 .
.
We will utilize the following control function which is also referred to as altering distance function.
Definition 1.5. [14] A function  is called an Altering distance function if the following properties are satisfied:
is called an Altering distance function if the following properties are satisfied:
1)  is monotone increasing and continuous2)
is monotone increasing and continuous2)  if and only if
if and only if 
For the use of control function in metric fixed point theory see some recent references ([15,16]).
2. Main Result
Recently fixed point theory in partially ordered metric spaces has greatly developed. Choudhury and Metiya [17] proved certain fixed point theorems for multi valued and single valued mappings in partially ordered metric spaces. They proved the following:
Theorem 2.1. Let 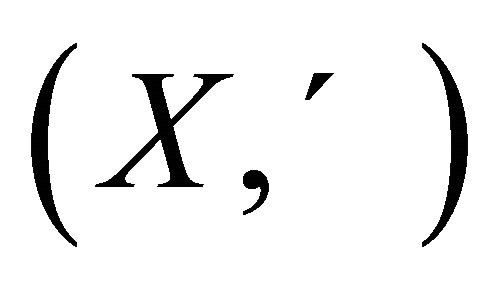 be a partially ordered set and suppose that there exists a metric d on X such that
be a partially ordered set and suppose that there exists a metric d on X such that  is a complete metric space. Let
is a complete metric space. Let 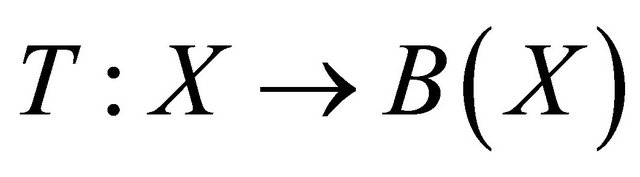 be a multi valued mappings such that the following conditions are satisfied:
be a multi valued mappings such that the following conditions are satisfied:
There exists  such that
such that 1) For
1) For  implies
implies 
2) If  is a non decreasing sequence in X, then
is a non decreasing sequence in X, then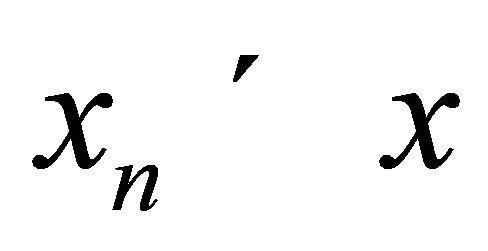 , for all n3)
, for all n3) for all comparable
for all comparable , where
, where  and
and  is an Altering distance function. Then T has a fixed point.
is an Altering distance function. Then T has a fixed point.
We prove the following theorem for four single-valued and multivalued mappings:
Theorem 2.2. Let  be a partially ordered set and suppose that there exists a metric d on X such that
be a partially ordered set and suppose that there exists a metric d on X such that  is a complete metric space. Let
is a complete metric space. Let  be single valued and
be single valued and  be multivalued mappings such that the following conditions are satisfied:
be multivalued mappings such that the following conditions are satisfied:
1) 
2)  and
and  are weakly compatible3) If
are weakly compatible3) If  is a strictly decreasing sequence in X, then
is a strictly decreasing sequence in X, then , for all n4)
, for all n4) for all comparable
for all comparable ,
, 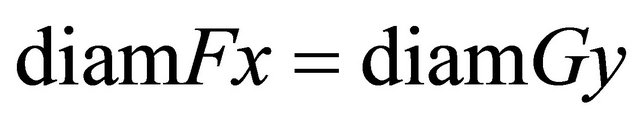 , where
, where  and
and  is an Altering distance function and suppose that one of
is an Altering distance function and suppose that one of  or
or 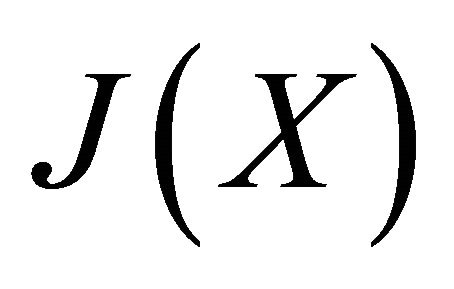 is complete. Then there exists a unique point
is complete. Then there exists a unique point  such that
such that

Proof: Let  be an arbitrary point of X. By 1) we choose a point
be an arbitrary point of X. By 1) we choose a point  such that
such that . For this point
. For this point , there exists a point
, there exists a point  such that
such that
 , and so on. Continuing in this manner we can define a sequence
, and so on. Continuing in this manner we can define a sequence  as follows
as follows
 (2.1)
(2.1)
We claim that 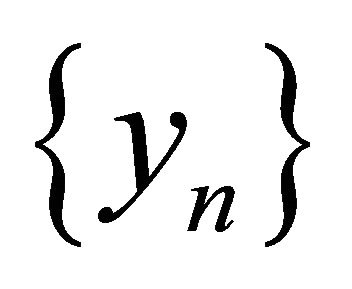 is a Cauchy sequence. For which two cases arise, either
is a Cauchy sequence. For which two cases arise, either  for some n, or
for some n, or , for each n.
, for each n.
Case I. If  for some n then,
for some n then,  for each
for each . For instance suppose
. For instance suppose . Then
. Then . Otherwise using 3), we get
. Otherwise using 3), we get

Since

It follows that
 (2.2)
(2.2)
Suppose that if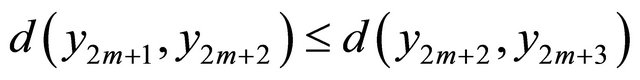 , for some positive integer n, then from (2.2), we have
, for some positive integer n, then from (2.2), we have

which implies that 
Hence  Similarly
Similarly  implie
implie  Proceeding in this manner, it follows that
Proceeding in this manner, it follows that  for each
for each , so that
, so that  for each
for each , for some n, and
, for some n, and  is a Cauchy sequence.
is a Cauchy sequence.
Case II. When  for each n. In this case, using 3), we obtain
for each n. In this case, using 3), we obtain

Since
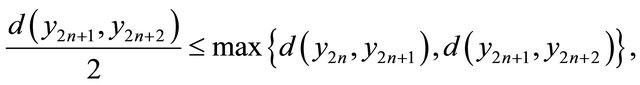
It follows that
 (2.3)
(2.3)
Now if  for each positive integer n, then from (2.3), we have
for each positive integer n, then from (2.3), we have

which implies that  contradicting our assumption that
contradicting our assumption that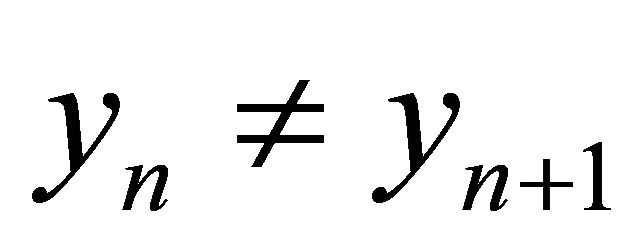 , for each n. Therefore
, for each n. Therefore  for all
for all 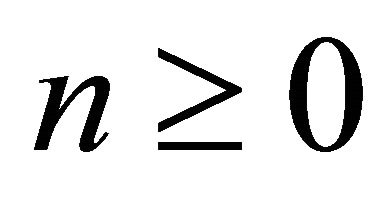 and
and  is strictly decreasing sequence of positive numbers and therefore tends to a limit
is strictly decreasing sequence of positive numbers and therefore tends to a limit . If possible suppose r > 0. Then for given
. If possible suppose r > 0. Then for given , there exists a positive integer N such that for each
, there exists a positive integer N such that for each , we have
, we have
 (2.4)
(2.4)
Taking the limit  in (2.3) and using the continuity of
in (2.3) and using the continuity of , we have or
, we have or

which is a contradiction unless . Hence
. Hence
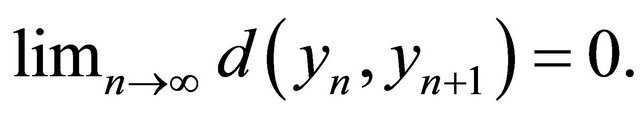 (2.5)
(2.5)
Next we show that  is a Cauchy sequence. Suppose it is not, then there exists an
is a Cauchy sequence. Suppose it is not, then there exists an 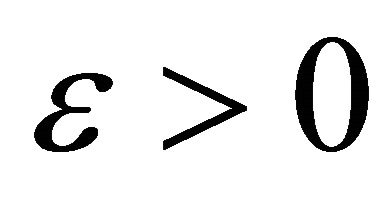 and since
and since
 there exists two sequences of positive numbers
there exists two sequences of positive numbers  and
and  such that for all positive integers k,
such that for all positive integers k,  and
and
 . Assuming that
. Assuming that 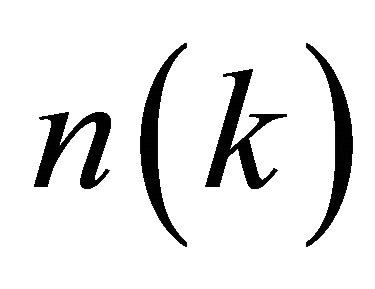 is the smallest positive integer, we get
is the smallest positive integer, we get 

Now,

i.e.
 (2.6)
(2.6)
Taking the limit as  in (2.6) and using (2.5), we have
in (2.6) and using (2.5), we have
 (2.7)
(2.7)
Again

and

Taking the limit as  and using (2.6) and (2.7), we have
and using (2.6) and (2.7), we have
 (2.8)
(2.8)
Again we have

and

Letting  and using (2.6) and (2.7), we have
and using (2.6) and (2.7), we have
 (2.9)
(2.9)
Similarly, we have .
.
For each positive integer k,  and
and  are comparable. Now using the monotone property of
are comparable. Now using the monotone property of  in 4), we have
in 4), we have

Letting  and using (2.6)-(2.9), and the continuity of
and using (2.6)-(2.9), and the continuity of , we have
, we have , which is a contradiction by virtue of property of
, which is a contradiction by virtue of property of . Therefore
. Therefore  and hence any subsequence thereof, is a Cauchy sequence.
and hence any subsequence thereof, is a Cauchy sequence.
Suppose  is complete. Since
is complete. Since 
is a subsequence of , by the above
, by the above  is Cauchy and
is Cauchy and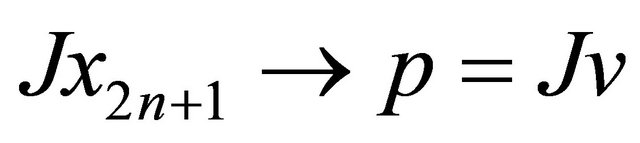 , for some
, for some .
.
We now show . For suppose
. For suppose 
Since  and
and  therefore,
therefore, . But
. But 
is a subsequence of the strictly decreasing sequence  which tends to the lim r = 0. Therefore
which tends to the lim r = 0. Therefore
 tends to limit r = 0 and hence
tends to limit r = 0 and hence
 implying
implying . Thus
. Thus . Now using
. Now using , we have
, we have

or

which is a contradiction. Consequently 
as .
.
In the same manner, it follows that  as
as  We now show
We now show . For this, in view of
. For this, in view of , we have
, we have

implies
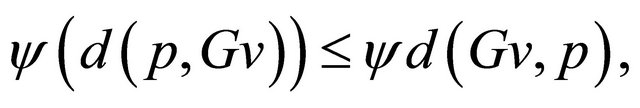
or

which is a contradiction. Consequently,  as
as . Hence
. Hence . Since
. Since  there exists some
there exists some  such that
such that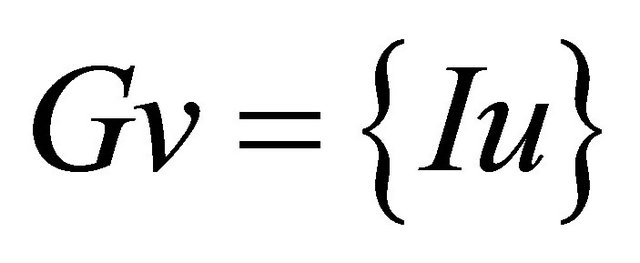 . Hence
. Hence . We now show
. We now show . For this, first we prove
. For this, first we prove . Suppose
. Suppose  then
then  . Then in accordance with
. Then in accordance with 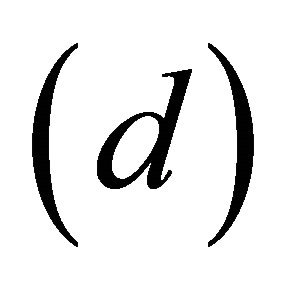 such that
such that

implies  while
while  . Therefore a contradiction arises. Hence
. Therefore a contradiction arises. Hence . But then
. But then , which, by
, which, by , implies
, implies 
Therefore Fu is a singleton. Since  and Fu is a singleton,
and Fu is a singleton, . Hence
. Hence

Since the pair  and
and  are weakly compatible,
are weakly compatible,

and

From the above, it is clear that Fp and Gp are singletons and 
We now show that . For instance, suppose
. For instance, suppose  then from
then from , we have
, we have

Implies as above  as
as . Hence
. Hence  and therefore
and therefore 
We now show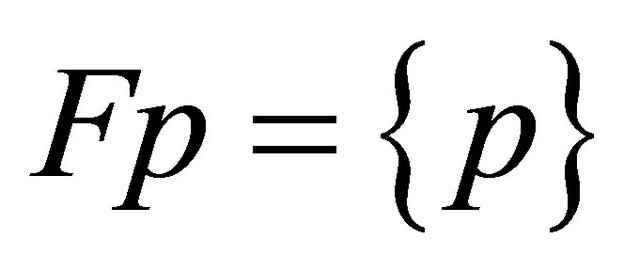 . For, suppose
. For, suppose . For this let
. For this let  in
in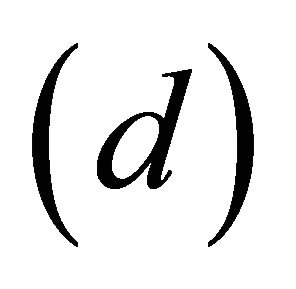 , we have
, we have

or
 which is a contradiction. Consequently
which is a contradiction. Consequently  as
as  Therefore
Therefore 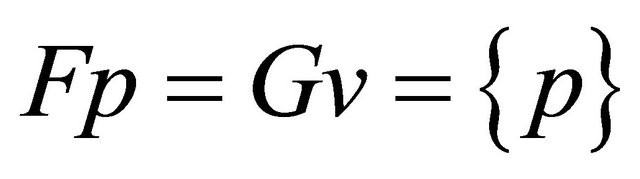 and hence
and hence

Let  be any point satisfying
be any point satisfying

Suppose  then from
then from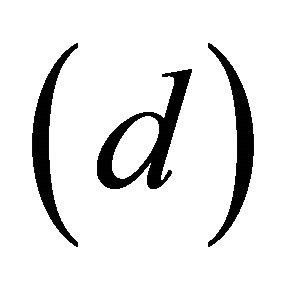 , we have
, we have
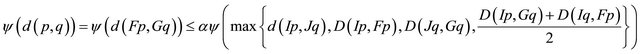 in view of
in view of 
 Hence
Hence .
.
Corollary 2.1. Let I be a self mapping of a metric space  and
and  a set valued mapping satisfying 1)'
a set valued mapping satisfying 1)' 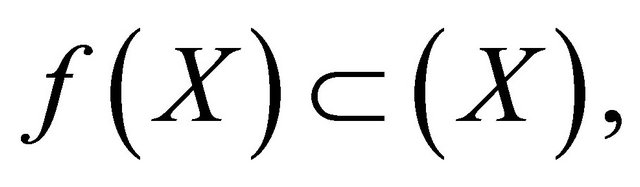
2)'  are weakly compatible3)'
are weakly compatible3)' for all comparable
for all comparable , where
, where  and
and 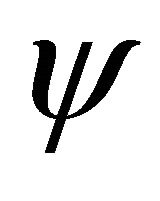 is an altering distance function. If
is an altering distance function. If  is complete subspace of X, there exists a unique point
is complete subspace of X, there exists a unique point 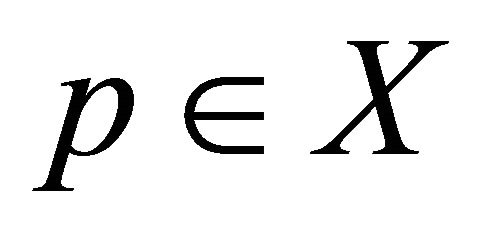 such that
such that 
Proof: Taking I = J and  in Theorem 2.2.
in Theorem 2.2.
Taking I = identity mapping in Corollary 2.1, we get the new corollary as follows:
Corollary 2.2. Let 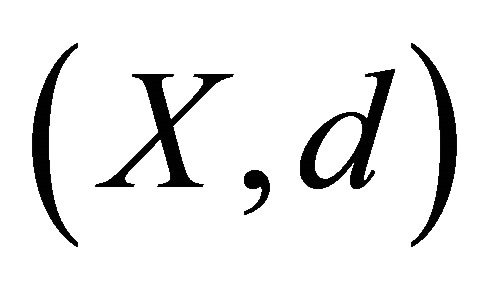 be a complete metric space and
be a complete metric space and  a set valued mapping satisfying
a set valued mapping satisfying

Then f has a unique fixed point in X.
Proof. Obvious.
Corollary 2.3. Let  be a partially ordered set and suppose that there exists a metric d on X such that
be a partially ordered set and suppose that there exists a metric d on X such that  is a complete metric space. Let
is a complete metric space. Let 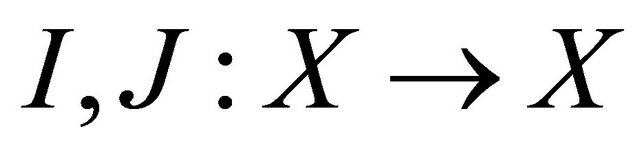 be single valued and
be single valued and  be multivalued mappings such that the following conditions are satisfied:
be multivalued mappings such that the following conditions are satisfied:
1)'' 
2)'' 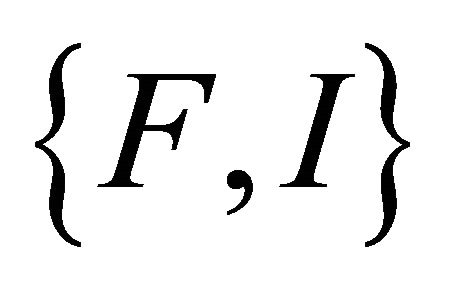 and
and  are weakly compatible3)'' if
are weakly compatible3)'' if 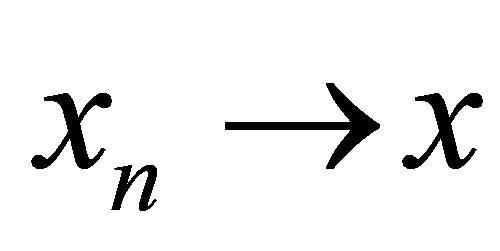 is a strictly decreasing sequence in X, then
is a strictly decreasing sequence in X, then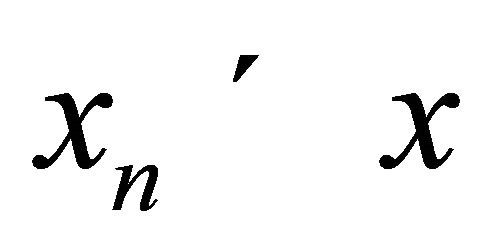 , for all n4)''
, for all n4)'' for all comparable
for all comparable ,
,  , where
, where  and
and  is an Altering distance function and suppose that one of
is an Altering distance function and suppose that one of 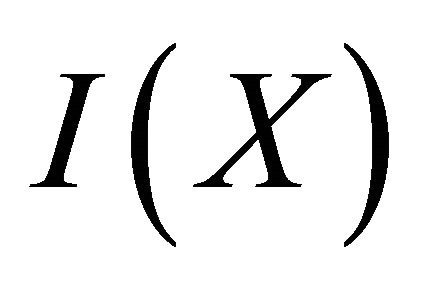 or
or  is complete. Then there exists a unique point
is complete. Then there exists a unique point 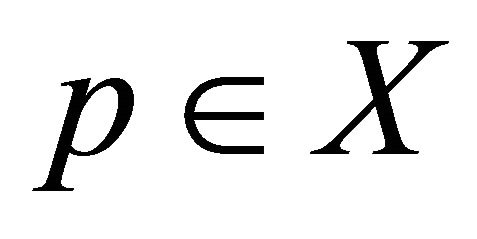 such that
such that

Example 2.1. Let  be a sub set of
be a sub set of  with the order
with the order  defined as for
defined as for
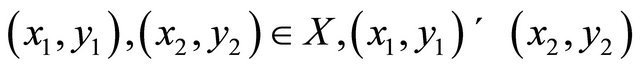
if and only if . Let
. Let  be given as
be given as

for .
.
The  is a complete metric space with the required properties of Theorem 2.2.
is a complete metric space with the required properties of Theorem 2.2.
Let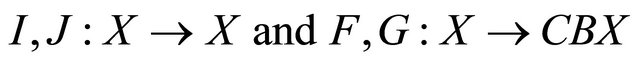 , be defined as follows:
, be defined as follows:


Let  defined as
defined as , and
, and . Then all the conditions in the Theorem 2.2 satisfied. Without loss of generality, we assume that
. Then all the conditions in the Theorem 2.2 satisfied. Without loss of generality, we assume that , we discuss the following cases.
, we discuss the following cases.
1) If ,
,  , then
, then  and
and

2) If  then
then , and
, and

3) If 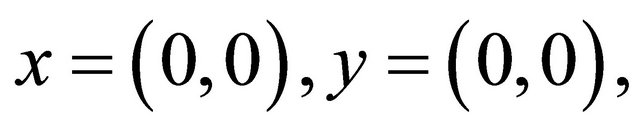 then
then , and
, and

4) If  then
then , and
, and

5) If  then
then  and
and
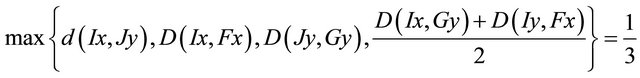
In all above cases, it is clearly shown that
 Hence the conditions of Theorem 2.2 are satisfied and shown that
Hence the conditions of Theorem 2.2 are satisfied and shown that  is a fixed point of I, J, F, and G.
is a fixed point of I, J, F, and G.
3. Acknowledgements
Dedicated to Professor H. M. Srivastava on his 71st Birth Anniversary.