Electromagnetic Oscillations in a Spherical Conducting Cavity with Dielectric Layers. Application to Linear Accelerators ()
1. Introduction
It has been shown [1-3] that, if a plane electromagnetic wave is scattered on a finite dielectric object, structural resonances can be excited in the object (e.g., whispering gallery modes). They are associated with very high amplitudes of oscillating EM fields in the dielectric and its vicinity. Their maxima exceed values reached in resonant cavities of typical linear accelerators by several orders of magnitude. Therefore, one can think of applying these fields to accelerate charged particles [1-3]. Many other applications of the whispering gallery modes are described in [4-6].
As for the proposals given in [1-3], both light produced by lasers and microwaves are conceivable. However, it is difficult to achieve the required synchronization of wave particle in the optical frequency range. In the microwave frequency range, this mechanism would require excessive total excitation energy and so may not be practical.
In this paper we demonstrate that the last mentioned problem can be overcome by locating the dielectric object in a resonant cavity. This appeals to traditional accelerating structures used in SLAC, see Figure 1. In the latter case, maximum amplitudes of accelerating fields are restricted by Joule heating losses in conducting walls and electric breakdown. In this connection, in existing accelerators (e.g., in LHC) one avoids sharp edges of the walls and uses superconductive resonant
 (a)
(a)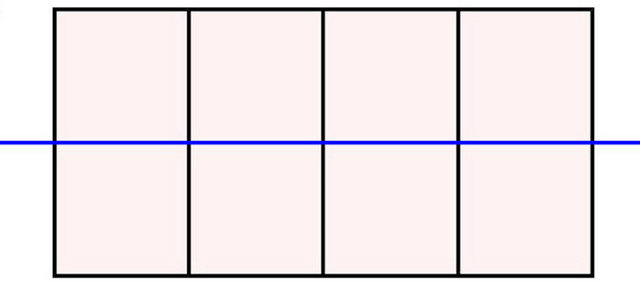 (b)
(b)
Figure 1. Proposed multi cell accelerator units (a) vs. those of SLAC (b), assuming the same electron transit time through the cavity.
cavities. Unfortunately, since superconductivity of the walls disappears if the magnetic field on the wall exceeds a critical value, the maximal values of accelerating fields in these highly complicated cavities are not much higher than those reached in SLAC.
The presence of a dielectric in the central part of the resonance cavity shifts the magnetic field maximum from regions close to the metallic wall towards the dielectric surface. This considerably lowers skin effect losses in the wall. Even though additional losses due to dielectric heating are introduced, total losses would nevertheless be lower if one could apply ultra low loss dielectrics (with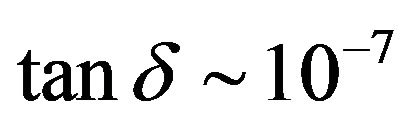 ) as described in [7,8]. In that case, a resonator quality reaching
) as described in [7,8]. In that case, a resonator quality reaching 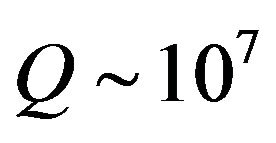 can be obtained, as compared to
can be obtained, as compared to  for SLAC.
for SLAC.
2. A Spherical Conductive Cavity with Dielectric Layers
Our approach to describe electromagnetic oscillations in a resonant cavity assumes that the cavity can be divided into regions in which the fields can be determined analytically. The resonant frequency is defined by the fact that the fields must satisfy boundary conditions at the cavity wall along with continuity conditions at the interfaces. This frequency will be determined by numerically solving the consistency condition for these requirements.
In general, we assume that the cavity is bounded by a conducting spherical surface, and filled concentrically with  either dielectric or vacuum layers. Each dielectric layer is assumed to be homogeneous. We introduce a spherical coordinate system
either dielectric or vacuum layers. Each dielectric layer is assumed to be homogeneous. We introduce a spherical coordinate system  with its origin at the cavity center. The layers are bounded by
with its origin at the cavity center. The layers are bounded by , up to
, up to  for the metallic boundary, see Figure 2.
for the metallic boundary, see Figure 2.

Figure 2. An example of a spherical cavity with dielectric layers (N = 4).
The harmonically oscillating electromagnetic fields in each concentric layer are described by Maxwell’s equations (Gaussian units, magnetic permeability , and complex fields proportional to
, and complex fields proportional to ):
):
 (1)
(1)
where
 (2)
(2)
 is the angular frequency, and
is the angular frequency, and  denotes complex dielectric permittivity
denotes complex dielectric permittivity
 (3)
(3)
These fields split into transverse electric (TE) or transverse magnetic (TM), which have no radial components of either field [9]. In an ideal resonator with perfectly conducting walls and perfect dielectrics, pure TE or TM modes can be excited. They will also be approximately valid in real resonators if their energy losses are not too high.
Using (9.116), and (9.119) in [9], which describe the vacuum TE field in spherical coordinates, and replacing there  we obtain the most general form of the TE field in the uniform dielectric:
we obtain the most general form of the TE field in the uniform dielectric:
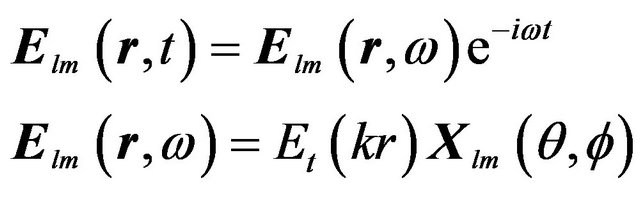 (4)
(4)
where
 (5)
(5)
 are vector spherical harmonics as defined by Eqation (9.119) in [9], and
are vector spherical harmonics as defined by Eqation (9.119) in [9], and

and 
are spherical Bessel and Neumann functions.
The corresponding magnetic induction can be determined from the first Maxwell Equation (1). Using also (10.60) in [9] we obtain
 (6)
(6)
where  involves both the transverse and radial component:
involves both the transverse and radial component:
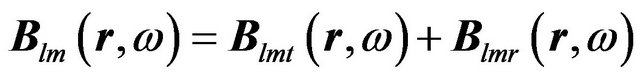 (7)
(7)
in which
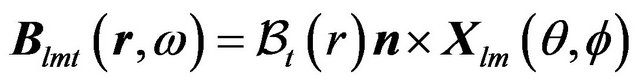 (8)
(8)
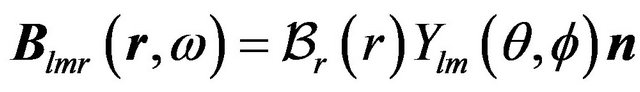 (9)
(9)
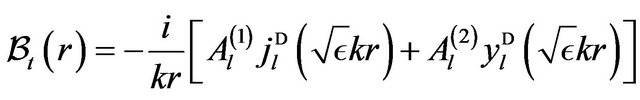 (10)
(10)
 (11)
(11)
Here  are spherical harmonics,
are spherical harmonics, 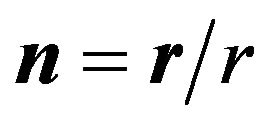 ,
, 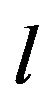 is a positive integer related to the integer
is a positive integer related to the integer  by
by 

and 
are derivatives of the Riccati-Bessel and Riccati-Neumann functions.
In a similar way, using (9.118), (9.119) and (10.60) in [9] along with the second Maxwell Equation (1), we obtain for the TM modes in the uniform dielectric:
 (12)
(12)
where
 (13)
(13)
 (14)
(14)
where  involves both the transverse, and radial component:
involves both the transverse, and radial component:
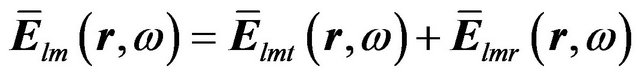 (15)
(15)
in which
 (16)
(16)
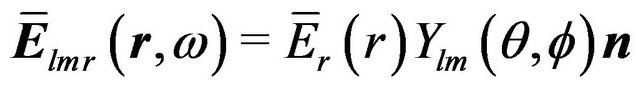 (17)
(17)
 (18)
(18)
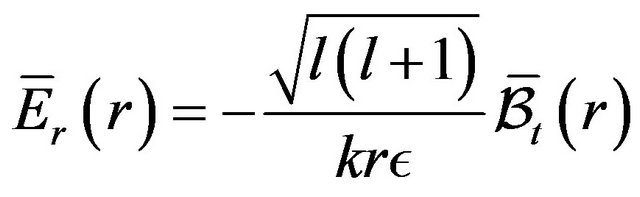 (19)
(19)
In our analysis we will admit small energy losses in both the wall and the dielectric layers. However, when calculating the resonant frequency of the cavity , these losses will be neglected. Thus the wall is assumed to be perfectly conducting. This means that it carries no electric or magnetic field. Then continuity of the tangential components of the electric field and the normal components of the magnetic induction at each interface require vanishing of these components at the boundary of
, these losses will be neglected. Thus the wall is assumed to be perfectly conducting. This means that it carries no electric or magnetic field. Then continuity of the tangential components of the electric field and the normal components of the magnetic induction at each interface require vanishing of these components at the boundary of  th layer at
th layer at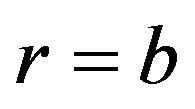 . In view of (4)-(9), and (12)-(19) this will be the case if the following boundary conditions at
. In view of (4)-(9), and (12)-(19) this will be the case if the following boundary conditions at  are fulfilled:
are fulfilled:
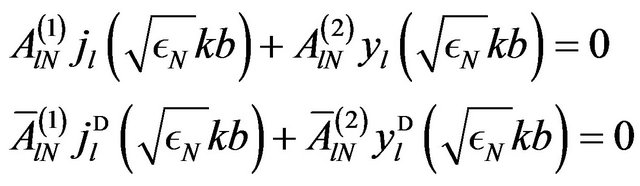 (20)
(20)
where the upper line refers to TE modes and the lower one to TM modes.
In the first layer which contains the origin 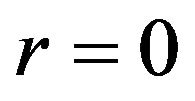 we must choose
we must choose
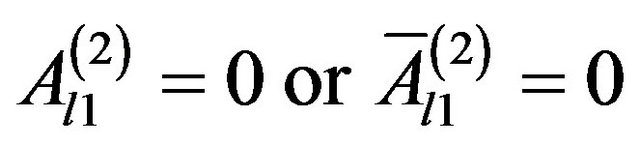 (21)
(21)
to avoid singularities of 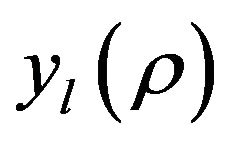 or
or  at
at .
.
In the simplest case of a spherical cavity filled completely with the dielectric (or vacuum), i.e.,  , the boundary conditions (20) lead to
, the boundary conditions (20) lead to
 (22)
(22)
where  This defines the resonant frequency
This defines the resonant frequency  of either TE or TM modes, depending only on
of either TE or TM modes, depending only on  and
and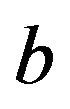 .
.
In the presence of layers ,
,  must also depend on
must also depend on etc. and therefore condition (22) cannot be fulfilled. In fact, for the same reason, we can assume that also the remaining functions in conditions (20) are non-vanishing. Therefore these conditions can be satisfied by choosing
etc. and therefore condition (22) cannot be fulfilled. In fact, for the same reason, we can assume that also the remaining functions in conditions (20) are non-vanishing. Therefore these conditions can be satisfied by choosing
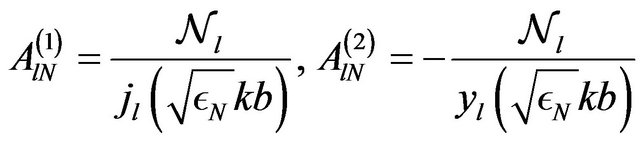 (23)
(23)
 (24)
(24)
for TE modes (upper line) or TM modes, where  and
and  are normalization factors.
are normalization factors.
At the interfaces between dielectrics, the following quantities must be continuous: the tangential components of the electric field and normal ones of the magnetic induction and furthermore, the tangential components of the magnetic induction, due to vanishing of the surface currents at the dielectric surface. For the TE modes, this leads to the following conditions at  :
:
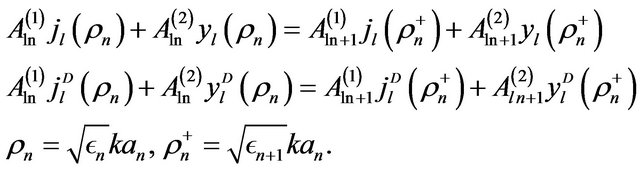 (25)
(25)
This can be written in matrix form
 (26)
(26)
where
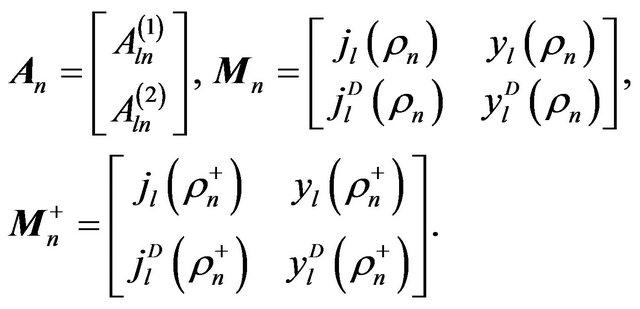 (27)
(27)
The  matrices are non-singular:
matrices are non-singular:
 (28)
(28)
where last equality follows from the fact that  and
and  are solutions of the Bessel equation
are solutions of the Bessel equation
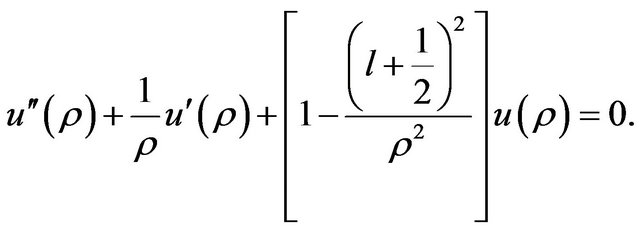
Multiplying (26) by
 (29)
(29)
we arrive at the recurrence relation
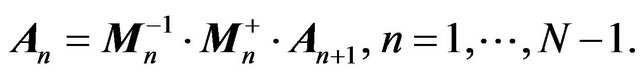 (30)
(30)
For the  th interface between dielectrics, this relation defines the vector
th interface between dielectrics, this relation defines the vector  at the lower layer in terms of that at the upper one. Using this relation successively for
at the lower layer in terms of that at the upper one. Using this relation successively for , we can express all
, we can express all  vectors in terms of
vectors in terms of
 (31)
(31)
i.e.,
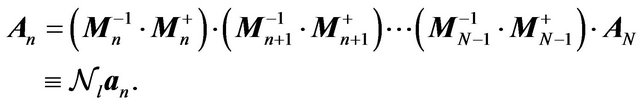 (32)
(32)
We recall that in the first layer we must satisfy , see (21). In view of this requirement, Equation (25) for
, see (21). In view of this requirement, Equation (25) for  can be written as
can be written as
 (33)
(33)
where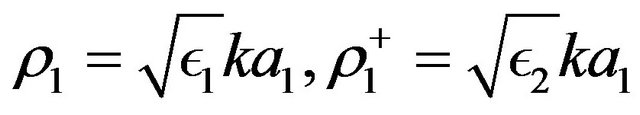 , and
, and  are components of the vector
are components of the vector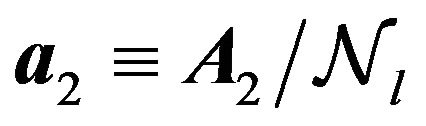 . This vector is defined by (32) and (31) if
. This vector is defined by (32) and (31) if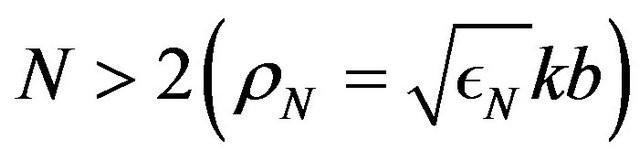 :
:
 (34)
(34)
For ,
,  is defined by (31), i.e., is given by the last factor in (34).
is defined by (31), i.e., is given by the last factor in (34).
The linear and homogeneous set of Equation (33) for  and
and 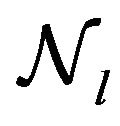 will have non-zero solutions if and only if its determinant vanishes,
will have non-zero solutions if and only if its determinant vanishes,
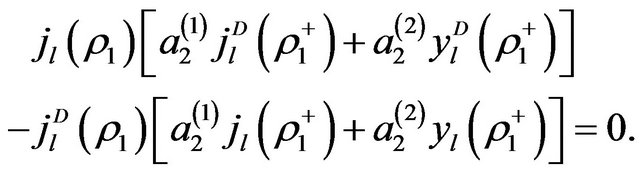 (35)
(35)
If this condition is fulfilled,  is given by either of Equation (33), which are equivalent. Like all remaining coefficients
is given by either of Equation (33), which are equivalent. Like all remaining coefficients  and
and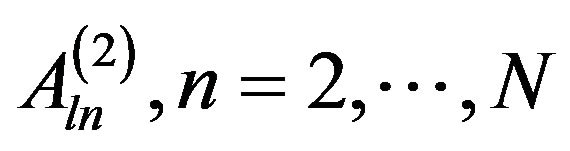 , also
, also 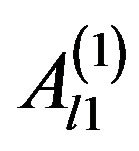 will be proportional to the normalization factor
will be proportional to the normalization factor , see (32) and (33).
, see (32) and (33).
If there are only two layers ,
,  and
and  in (33) and (35) are given by (31) and the resonant frequency
in (33) and (35) are given by (31) and the resonant frequency  defined by (35) can be found from
defined by (35) can be found from
 (36)
(36)
and
 (37)
(37)
By replacing in (25)-(37)
 (38)
(38)
for any 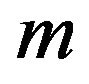 and
and , we obtain the corresponding equations for the TM modes.
, we obtain the corresponding equations for the TM modes.
Any standard software like Mathematica or Maple can be used to solve the non-linear Equations (35) or (36) defining the resonant frequency , along with the pertinent linear algebra for
, along with the pertinent linear algebra for . We did it for
. We did it for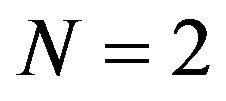 , see the following section, and also for
, see the following section, and also for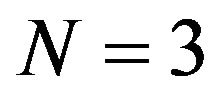 , by using Mathematica.
, by using Mathematica.
Note that for the TM modes, where  in (19) is continuous at each dielectric interface,
in (19) is continuous at each dielectric interface,  will have jumps, due to discontinuities in
will have jumps, due to discontinuities in . However, the radial component of the electric displacement
. However, the radial component of the electric displacement  will be continuous. This will also be true of the TE modes where the radial displacement is identically zero. These facts imply the vanishing of surface charges at each dielectric interface. And this in turn means that the multi-layer dielectric structure resembles (and can approximate) a smooth dielectric with some permittivity profile
will be continuous. This will also be true of the TE modes where the radial displacement is identically zero. These facts imply the vanishing of surface charges at each dielectric interface. And this in turn means that the multi-layer dielectric structure resembles (and can approximate) a smooth dielectric with some permittivity profile , in spite of jumps in
, in spite of jumps in .
.
It was pointed out to us by Paul Martin of SIAM, that our matrix Equation (26), which can be used to relate the EM fields of a given mode for two layers of a stratified sphere, is not new. It was probably first used by A. Moroz [10] when calculating forced oscillations in such a sphere but without a conducting wall, induced by an oscillating electric dipole. In this application, the frequency  is arbitrary.
is arbitrary.
3. A Spherical Conductive Cavity with a Dielectric Sphere
The general theory given in the previous section will now be illustrated by calculations pertinent to the TE modes in a spherical cavity with a dielectric sphere of radius  and dielectric permittivity
and dielectric permittivity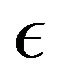 , i.e., for
, i.e., for
 , and
, and .
.
Fields in such a system will be described by Equations (4)-(9) both in the sphere and the surrounding vacuum. In view of (21) and (23) their radial profiles will be given by
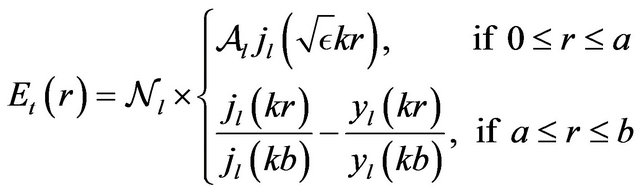 (39)
(39)
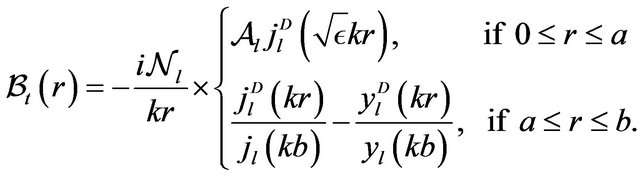 (40)
(40)
Replacing  and
and  in (36) and (37), we obtain equations defining the resonant frequency
in (36) and (37), we obtain equations defining the resonant frequency  and the amplitude coefficient
and the amplitude coefficient .
.
We verified that for , the average energies associated with the electric and the magnetic field in the cavity are equal:
, the average energies associated with the electric and the magnetic field in the cavity are equal:
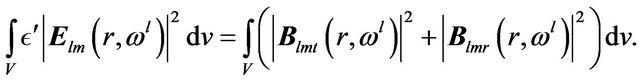 (41)
(41)
(This was a check on the correctness of our formulas and accuracy of calculations.) The normalization constant 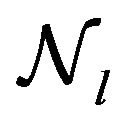 was chosen so as to satisfy:
was chosen so as to satisfy:
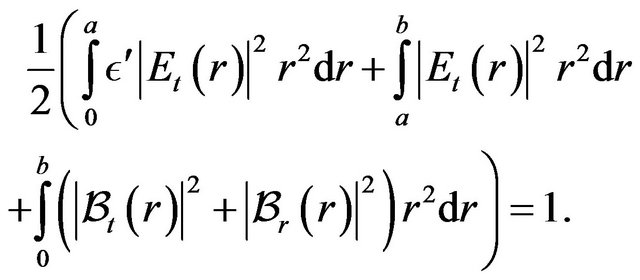 (42)
(42)
(The corresponding average energy associated with the electric and the magnetic field over our cavity is  erg.)
erg.)
In Figure 3, 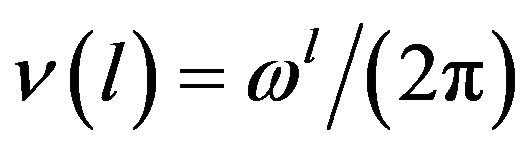 as a function of
as a function of  is presented for three spherical cavities with dielectric spheres. Note that
is presented for three spherical cavities with dielectric spheres. Note that  is
is  independent (due to degeneracy). This fact is one of the reasons why the spherical resonator shown in Figure 1 cannot be used in the final project of a real accelerator even though it is very convenient for a general analysis. The degeneration in question can be broken e.g., by replacing the spherical resonator by an ellipsoidal one, or shifting the center of the dielectric sphere. Another possibility could be to use an anisotropic dielectric. In any case, however, a separate numerical analysis would be necessary.
independent (due to degeneracy). This fact is one of the reasons why the spherical resonator shown in Figure 1 cannot be used in the final project of a real accelerator even though it is very convenient for a general analysis. The degeneration in question can be broken e.g., by replacing the spherical resonator by an ellipsoidal one, or shifting the center of the dielectric sphere. Another possibility could be to use an anisotropic dielectric. In any case, however, a separate numerical analysis would be necessary.
In Figure 4 we give an example of radial functions in the equations describing fields in our spherical cavity with a dielectric sphere, (4), (8) and (9). Large values of these functions in a vicinity of the dielectric boundary can be observed.
3.1. The Motion of Relativistic Electrons
The trajectory  of a relativistic electron crossing the spherical cavity shown in Figure 1 can be parametrized by the electron's closest approach
of a relativistic electron crossing the spherical cavity shown in Figure 1 can be parametrized by the electron's closest approach 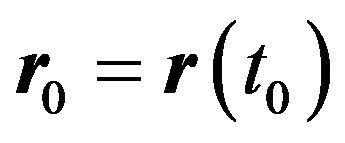 and electron velocity
and electron velocity :
:
 (43)
(43)
The origin of the Cartesian coordinate system  was chosen at the center of the dielectric sphere, and the electron moving along the
was chosen at the center of the dielectric sphere, and the electron moving along the 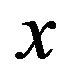 axis was passing just above the dielectric sphere as shown in Figure 1. We chose
axis was passing just above the dielectric sphere as shown in Figure 1. We chose
 (44)
(44)
The effective accelerating field felt by the electron as it passes through the cavity,  , is equal to the real part of
, is equal to the real part of 
 (45)
(45)
where  is the electron trajectory segment within the cavity,
is the electron trajectory segment within the cavity,  is the
is the  component of the electric field
component of the electric field  given by (4) and
given by (4) and  is given by (43). Thus
is given by (43). Thus
 (46)
(46)
Maximal acceleration is obtained if
if 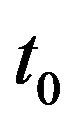 is chosen so that the accelerating phase
is chosen so that the accelerating phase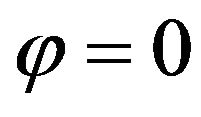 . With this choice, the relativistic electron is never decelerated within the spherical cavity, see Figure 5, where two examples are given. Typical results for
. With this choice, the relativistic electron is never decelerated within the spherical cavity, see Figure 5, where two examples are given. Typical results for  obtained with our normalization (42) are shown in Figures 6 and 7.
obtained with our normalization (42) are shown in Figures 6 and 7.
The electromagnetic field given by the real parts of (4), (8) and (9) is strongly non-uniform. Therefore one should check how much the relativistic electron will deflect from the assumed trajectory  given by (43), due to interaction with this field. A nice feature of our model is that the field in question is described analytically by (4)-(9) so that the pertinent equations of the transversal motion can easily be integrated numerically.
given by (43), due to interaction with this field. A nice feature of our model is that the field in question is described analytically by (4)-(9) so that the pertinent equations of the transversal motion can easily be integrated numerically.
In a real accelerator, where we are dealing with an electron beam of finite cross section, the electromagnetic fields  and
and  acting on each electron will be superpositions of the external fields and the fields due to the electron charge and current. However, in the lowest approximation (and particularly for not too large beam densities) the latter fields can be neglected. Furthermore, if as in our case, the transversal deflections are small, the deflecting fields can be calculated on the unperturbed trajectory given by (43). It will also be assumed that the electron mass
acting on each electron will be superpositions of the external fields and the fields due to the electron charge and current. However, in the lowest approximation (and particularly for not too large beam densities) the latter fields can be neglected. Furthermore, if as in our case, the transversal deflections are small, the deflecting fields can be calculated on the unperturbed trajectory given by (43). It will also be assumed that the electron mass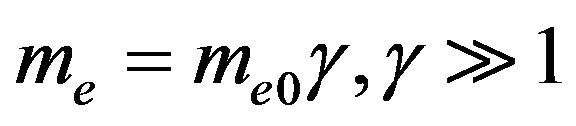 , is time independent within the spherical cavity. With these approximations, and within the Cartesian coordinate system
, is time independent within the spherical cavity. With these approximations, and within the Cartesian coordinate system  with its center at
with its center at , the
, the 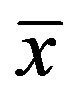 axis along the unperturbed trajectory, and the
axis along the unperturbed trajectory, and the  axis along
axis along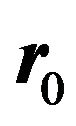 , the electron’s transversal motion will be described by
, the electron’s transversal motion will be described by
 (47)
(47)
 (48)
(48)
where , the field components
, the field components 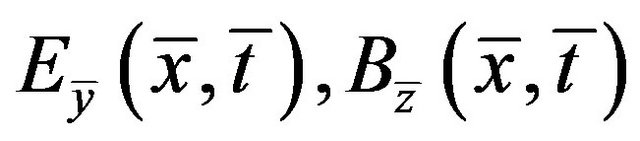 , etc. are given by the real parts of Equations (4), (8) and (9), taken at
, etc. are given by the real parts of Equations (4), (8) and (9), taken at , and
, and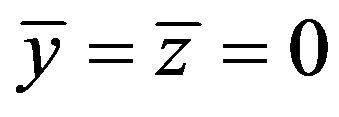 . Integrating these equations with zero initial conditions we end up with
. Integrating these equations with zero initial conditions we end up with 
 (49)
(49)
 (50)
(50)
 (51)
(51)
where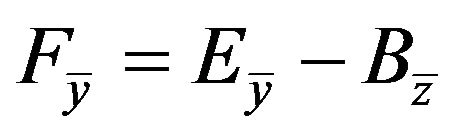 , and
, and .
.
In Figures 8 and 9 we give an example of the coordinates  and
and  of the deflecting force. They correspond to
of the deflecting force. They correspond to  cm,
cm, 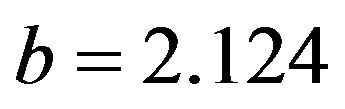 cm, and
cm, and , for which the the accelerating field will be our reference value
, for which the the accelerating field will be our reference value
 (52)
(52)
It can be seen that if the accelerating phase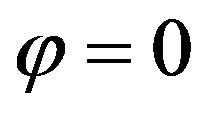 , both
, both  and
and  are odd functions. Therefore in this case of maximal acceleration, there will be no transversal velocity increments over the cavity,
are odd functions. Therefore in this case of maximal acceleration, there will be no transversal velocity increments over the cavity,  . At the same time the velocity components
. At the same time the velocity components  and
and 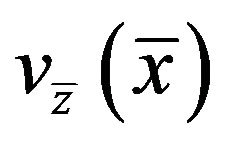 in (51) will be even functions of
in (51) will be even functions of  tending to zero as
tending to zero as . Hence the transversal deflections
. Hence the transversal deflections  and
and  will be increasing functions tending to constants as
will be increasing functions tending to constants as , see Figure 10(a).
, see Figure 10(a).
For the worst case of accelerating phase 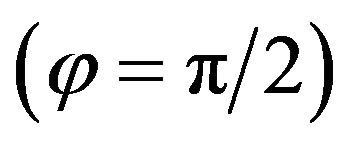 for which
for which 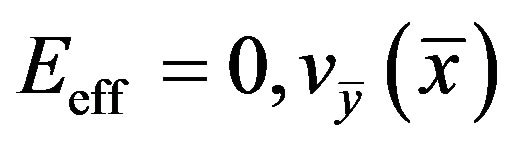 and
and  will be increasing functions soon reaching their limiting values
will be increasing functions soon reaching their limiting values  and
and  for
for . The corresponding transversal motions
. The corresponding transversal motions  and
and  will soon become uniform for
will soon become uniform for , leading to much larger deflections at
, leading to much larger deflections at , see Figure 10(b).
, see Figure 10(b).
The actual transversal deflections per cavity in an accelerator involving our spherical cavities can be obtained by multiplying the normalized values given in Figure 10 by the factor
 (53)
(53)
where  is given by (52),
is given by (52),  is the assumed value of the effective accelerating field, and
is the assumed value of the effective accelerating field, and . For large values of
. For large values of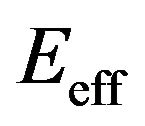 , small
, small 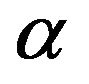 requires
requires 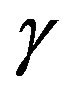 to be sufficiently large. Assuming that
to be sufficiently large. Assuming that  , see Figure 10(a) is not larger than
, see Figure 10(a) is not larger than 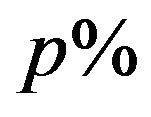 of the spacing between the dielectric sphere and the electron trajectory,
of the spacing between the dielectric sphere and the electron trajectory,  cm, the required minimal electron energy is given by
cm, the required minimal electron energy is given by
 (54)
(54)
Thus, if we assume that  MV/m, the transversal displacements will be smaller than
MV/m, the transversal displacements will be smaller than 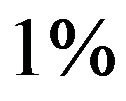 of the spacing in question, if the electron energy
of the spacing in question, if the electron energy  GeV, i.e., for typical output energies from SLAC. Whether the real dielectric can withstand this value of
GeV, i.e., for typical output energies from SLAC. Whether the real dielectric can withstand this value of  is another question beyond the scope of this paper. More comments will be given later on.
is another question beyond the scope of this paper. More comments will be given later on.
3.2. Quality Factors
An important parameter of any linear accelerator is the quality  of its resonant cavities:
of its resonant cavities:
 (55)
(55)
where  is the resonant angular frequency of the ideal cavity
is the resonant angular frequency of the ideal cavity ,
, 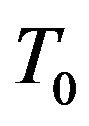 is the corresponding reso-
is the corresponding reso-
nant period,  is the time-averaged energy stored in the cavity
is the time-averaged energy stored in the cavity 
 (56)
(56)
and  is time-averaged cavity power loss.
is time-averaged cavity power loss.
The power loss caused by the skin current in the metallic wall bounded by the surface 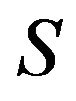 is given by
is given by
 (57)
(57)
where
 (58)
(58)
 is the skin depth,
is the skin depth,  is conductivity of the wall, and the magnetic field intensity
is conductivity of the wall, and the magnetic field intensity  refers to the ideal cavity, i.e., its normal component is vanishing
refers to the ideal cavity, i.e., its normal component is vanishing .
.
The quality of the cavity related to losses in the metallic wall is thus given by
 (59)
(59)
Using the fact that at resonance, the averaged energies stored in the electric and magnetic fields are equal, see (41), we end up with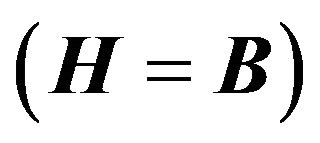 :
:
 (60)
(60)
This formula is quite general, and in particular can also be used for a traditional cylindrical cavity of radius 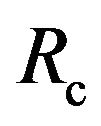 and height
and height . In that case, the cylindrically symmetric
. In that case, the cylindrically symmetric 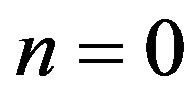 TM mode used for acceleration is given by
TM mode used for acceleration is given by
 (61)
(61)
 (62)
(62)
where ,
,  is a Bessel function, and
is a Bessel function, and  and
and  are cylindrical coordinates (cylindrical axis along
are cylindrical coordinates (cylindrical axis along ).
).
The vanishing of  on an ideally conducting cylindrical wall requires that
on an ideally conducting cylindrical wall requires that  (the smallest zero of
(the smallest zero of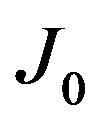 ) which defines the angular resonant frequency in terms of
) which defines the angular resonant frequency in terms of . Equations (62) and (60) lead to the well known formula for the quality of the cylindrical pill box cavity
. Equations (62) and (60) lead to the well known formula for the quality of the cylindrical pill box cavity
 (63)
(63)
For the SLAC pill box cavity shown in Figure 1 ( and
and  for copper wall in room-temperature), this formula leads to
for copper wall in room-temperature), this formula leads to . The corresponding values for spherical cavities with ideal dielectric spheres and the same values of
. The corresponding values for spherical cavities with ideal dielectric spheres and the same values of 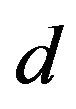 and
and  reach much larger values, see Figure 11.
reach much larger values, see Figure 11.
In the presence of the dielectric sphere, one is also dealing with losses due to an imperfect dielectric specified by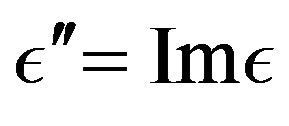 . The non-vanishing value of
. The non-vanishing value of  leads to
leads to , for
, for 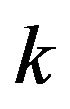 defined by (35). In view of Equation (2) this implies a complex value of
defined by (35). In view of Equation (2) this implies a complex value of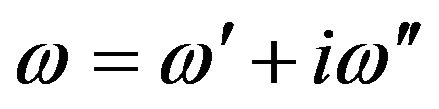 .
.
For the fields given by (4)-(9), we obtain

where  for the energy
for the energy  being dissipated rather than generated. Using this result we find for the power losses in the dielectric:
being dissipated rather than generated. Using this result we find for the power losses in the dielectric:

In view of (55), the corresponding quality will thus be given by
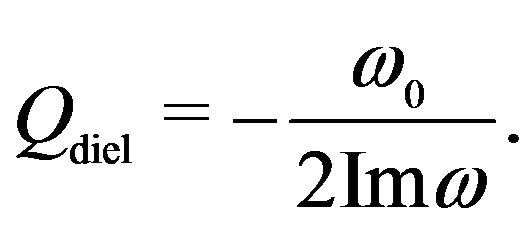 (64)
(64)
This value is of the order of . It is approximately
. It is approximately  independent.
independent.
In our calculations we took  and
and . Dielectrics with such ultra small losses were investigated in [8].
. Dielectrics with such ultra small losses were investigated in [8].
The total power loss in the spherical cavity encasing the dielectric sphere  is due to the power loss in the metallic wall and that in the dielectric sphere:
is due to the power loss in the metallic wall and that in the dielectric sphere:
 (65)
(65)
Dividing both sides of this relation by  and using (55) we obtain
and using (55) we obtain

Figure 11. The quality  vs.
vs.  for three spherical cavities with ideal dielectric spheres (see Figure 7).
for three spherical cavities with ideal dielectric spheres (see Figure 7).
 (66)
(66)
where  is the total Q-factor of the spherical cavity. Values of
is the total Q-factor of the spherical cavity. Values of  versus
versus  for three spherical cavities with dielectric spheres and
for three spherical cavities with dielectric spheres and  cm are shown in Figure 12. They are about three orders of magnitude larger than
cm are shown in Figure 12. They are about three orders of magnitude larger than .
.
In a real accelerator, openings in the metallic wall are necessary for free penetration of the cavity by the electron beam, and to enable coupling between neighboring cavities. This will lower the quality  but should have little effect on the total quality of the spherical cavity
but should have little effect on the total quality of the spherical cavity . The latter is defined by losses in the dielectric, see (66) where
. The latter is defined by losses in the dielectric, see (66) where . The resonant frequency should not be drastically changed either, as the EM fields at the iris
. The resonant frequency should not be drastically changed either, as the EM fields at the iris are very small fractions of their maxima, see Figure 4.
are very small fractions of their maxima, see Figure 4.
3.3. Discussion and Summary
When comparing the effective accelerating fields in the traditional pill box cavity with that in our spherical cavities with dielectric spheres, we first assume that , the time-averaged energy stored in the cavity, see (56), is the same in both situations. Therefore the normalization factor
, the time-averaged energy stored in the cavity, see (56), is the same in both situations. Therefore the normalization factor  in (61) and (62) will first be chosen so that
in (61) and (62) will first be chosen so that
 (67)
(67)
see (42) ( erg).
erg).
The complex effective accelerator field 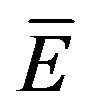 for the cylindrical resonator shown in Figure 1
for the cylindrical resonator shown in Figure 1 is given by the right hand side of (45) in which
is given by the right hand side of (45) in which  is defined by (61) with
is defined by (61) with , and
, and . The result is
. The result is
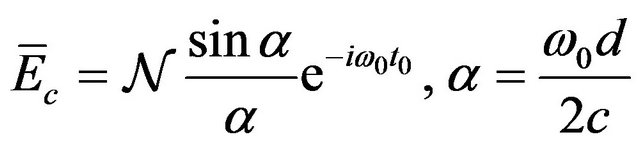 (68)
(68)

Figure 12. The quality  vs.
vs.  for three spherical cavities with dielectric spheres (see Figure 7).
for three spherical cavities with dielectric spheres (see Figure 7).
where  is the time at which the electron passes the center of the cavity.
is the time at which the electron passes the center of the cavity.
We now denote by 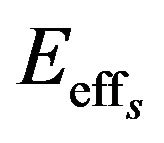 and
and 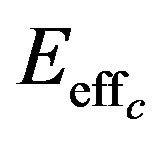 the maximal effective accelerating fields (equal to
the maximal effective accelerating fields (equal to ) for the spherical cavity with a dielectric sphere and the traditional cylindrical cavity, for any values of the average energies in the cavities,
) for the spherical cavity with a dielectric sphere and the traditional cylindrical cavity, for any values of the average energies in the cavities, 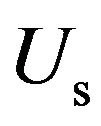 and
and . In view of the fact that
. In view of the fact that 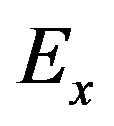 in (61) is proportional to
in (61) is proportional to 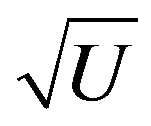 we can write, using the definition (55) of
we can write, using the definition (55) of ,
,
 (69)
(69)
where , the “gain factor”, is given by
, the “gain factor”, is given by
 (70)
(70)
Here  and
and  are the resonant frequencies of the spherical and the cylindrical cavities
are the resonant frequencies of the spherical and the cylindrical cavities  and
and  and
and  are the corresponding power losses. They are equal to the powers that must be supplied from external sources to sustain the oscillations. They should be as large as possible to avoid breakdown in the dielectric or at the metallic wall. Further research is necessary to give an estimate of the ratio
are the corresponding power losses. They are equal to the powers that must be supplied from external sources to sustain the oscillations. They should be as large as possible to avoid breakdown in the dielectric or at the metallic wall. Further research is necessary to give an estimate of the ratio . We can only hope that it is not smaller than unity.
. We can only hope that it is not smaller than unity.
For our typical SLAC pill box cavity shown in Figure 1  we obtain
we obtain  and
and
 kV/m to be used in (70). The resulting values of the gain factor are shown in Figure 13.
kV/m to be used in (70). The resulting values of the gain factor are shown in Figure 13.
The results of our calculation are shown in Figures 3-13 for three reasonable values of
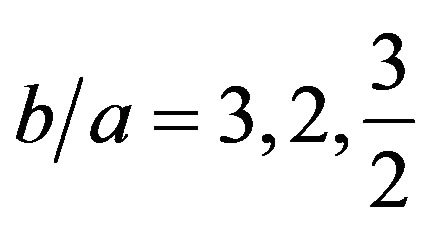 .
.
The electron trajectory segment inside the cavity shown in Figure 1 was equal to the typical length of the pill-box cavity of SLAC (4 cm). Calculations were performed for various values of  and
and . The optimal parameters found were:
. The optimal parameters found were:  cm,
cm,  cm, and
cm, and .
.
4. Conclusion
An electric field, intensified by structural resonance, can be used to accelerate electrons. This is demonstrated here by placing a dielectric sphere concentrically inside a spherical resonator, in which an appropriate whispering gallery mode is excited. A strong, accelerating field appears next to the surface of the dielectric. At the same time, the tangential component of the magnetic field at the wall of the resonator is minimal. This makes losses at the metallic walls negligible without engaging expensive cryogenic systems ensuring superconductivity of the walls. The Q factor of the resonator only depends on losses in the dielectric. For existing dielectrics, this gives a Q factor three orders of magnitude better than obtained in existing cylindrical cavities. Furthermore, for the proposed spherical cavity, all field components at the metallic wall are either zero or very small, see Figure 4. Therefore, one can expect the proposed spherical cavity to be less prone to electrical breakdowns than the traditional cylindrical cavity.
5. Acknowledgements
The authors would like to thank Professor  Kuliński for useful discussions.
Kuliński for useful discussions.