Approximate Method of Riemann-Hilbert Problem for Elliptic Complex Equations of First Order in Multiply Connected Unbounded Domains ()
 (0.1)
(0.1)
with the boundary conditions
 (0.2)
(0.2)
in a multiply connected unbounded domain D, the above boundary value problem will be called Problem A. If the complex Equation (0.1) satisfies the conditions similar to Condition C of (1.1), and the boundary condition (0.2) satisfies the conditions similar to (1.5), then we can obtain approximate solutions of the boundary value problems (0.1) and (0.2). Moreover the error estimates of approximate solutions for the boundary value problem is also given. The boundary value problem possesses many applications in mechanics and physics etc., for instance from (5.114) and (5.115), Chapter VI, [1], we see that Problem A of (0.1) possesses the important application to the shell and elasticity.
1. Formulation of Elliptic Equations and Boundary Value Problem
Let  be an
be an  -connected domain including the infinite point with the boundary
-connected domain including the infinite point with the boundary  in
in where
where . Without loss of generality, we assume that
. Without loss of generality, we assume that  is a circular domain in
is a circular domain in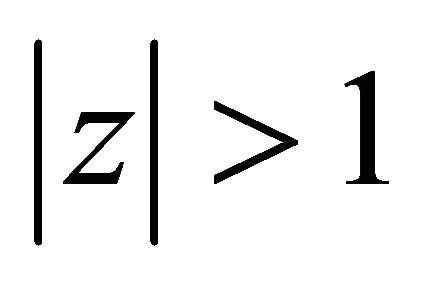 , where the boundary consists of
, where the boundary consists of  circles
circles
 ,
, 
and . In this article, the notations are as the same in References [1-6]. We discuss the nonlinear uniformly elliptic complex equation of first order
. In this article, the notations are as the same in References [1-6]. We discuss the nonlinear uniformly elliptic complex equation of first order
 (1.1)
(1.1)
which is the complex form of the real nonlinear elliptic system of first order equations
 (1.2)
(1.2)
under certain conditions (see [3]). Suppose that the complex Equation (1.1) satisfies the following conditions, namely Condition C: 1) 
 are measurable in
are measurable in  for all continuous functions
for all continuous functions 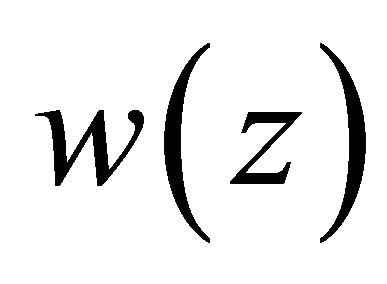 on
on 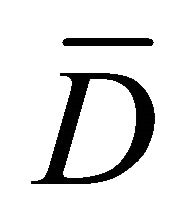 and all measurable functions
and all measurable functions
 and satisfy
and satisfy
 (1.3)
(1.3)
where  are non-negative constants.
are non-negative constants.
2) The above functions are continuous in  for almost every point
for almost every point  and
and  for
for 
3) The complex Equation (1.1) satisfies the uniform ellipticity condition, i.e. for any , the following inequality in almost every point
, the following inequality in almost every point 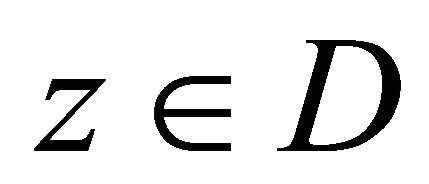 holds:
holds:
 (1.4)
(1.4)
in which  is a non-negative constant.
is a non-negative constant.
Problem A: The Riemann-Hilbert boundary value problem for the complex Equation (1.1) may be formulated as follows: Find a continuous solution  of (1.1) on
of (1.1) on  satisfying the boundary condition
satisfying the boundary condition
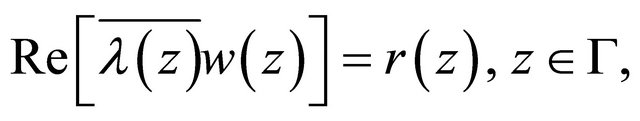 (1.5)
(1.5)
where  and
and  satisfy the conditions
satisfy the conditions
 (1.6)
(1.6)
in which 
 are non-negative constants.
are non-negative constants.
This boundary value problem for (1.1) with  and
and  will be called Problem
will be called Problem  The integer
The integer

is called the index of Problem  and Problem
and Problem 
Due to when the index  Problem
Problem  may not be solvable, when
may not be solvable, when  the solution of Problem
the solution of Problem  is not necessarily unique. Hence we put forward some well posednesses of Problem
is not necessarily unique. Hence we put forward some well posednesses of Problem  with modified boundary conditions.
with modified boundary conditions.
Problem B1: Find a continuous solution  of the complex Equation (1.1) in
of the complex Equation (1.1) in  satisfying the boundary condition
satisfying the boundary condition
 (1.7)
(1.7)
where

(1.8)
in which  are unknown real constants to be determined appropriately. In addition, we may assume that the solution
are unknown real constants to be determined appropriately. In addition, we may assume that the solution  satisfies the following side conditions (point conditions)
satisfies the following side conditions (point conditions)
 (1.9)
(1.9)
where

are distinct points, and  are all real constants satisfying the conditions
are all real constants satisfying the conditions
 (1.10)
(1.10)
herein  is a nonnegative constant.
is a nonnegative constant.
Now, we give the second well posed-ness of Problem .
.
Problem B2: If the point condition (1.9) in Problem  is replaced by the integral conditions
is replaced by the integral conditions
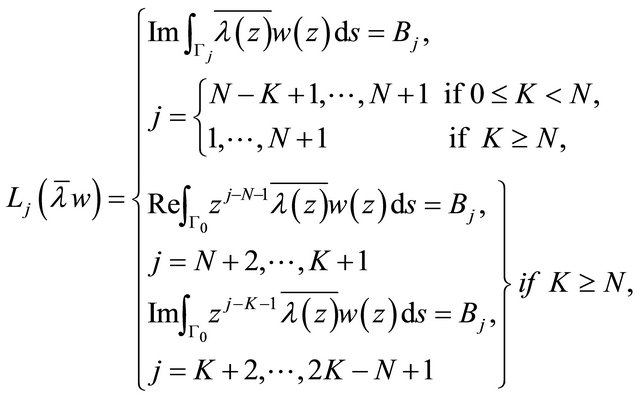
(1.11)
respectively, where  are real constants satisfying the conditions
are real constants satisfying the conditions
 (1.12)
(1.12)
in which  is a nonnegative real constant.
is a nonnegative real constant.
For convenience, we sometimes will subsume the integral conditions or the point conditions under boundary conditions.
2. A Priori Estimates of Solutions of Boundary Value Problem
First of all, we give a representation theorem of solutions for Problem  and for Problem
and for Problem 
Theorem 2.1. Suppose that the complex Equation (1.1) satisfies Condition C, and  is any solution of Problem
is any solution of Problem  (or Problem
(or Problem ) for (1.1). Then
) for (1.1). Then  is representable by
is representable by
 (2.1)
(2.1)
where  is a homeomorphism on
is a homeomorphism on , which quasiconformally maps D onto an
, which quasiconformally maps D onto an  -connected circular domain G with boundary
-connected circular domain G with boundary  where the
where the
 are located in
are located in  by
by
 and
and 
 is an analytic function in G,
is an analytic function in G,  and its inverse function
and its inverse function  satisfy the estimates
satisfy the estimates
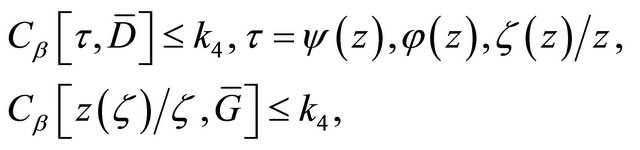 (2.2)
(2.2)
 (2.3)
(2.3)
 (2.4)
(2.4)
in which 
 are non-negative constants,
are non-negative constants, 
Proof. Similarly to Theorem 2.4, Chapter 2 in [3], we substitute the solution  of Problem
of Problem  (or Problem
(or Problem ) into the coefficients of the complex Equation (1.1) and consider the following system
) into the coefficients of the complex Equation (1.1) and consider the following system
 (2.5)
(2.5)
 (2.6)
(2.6)
 (2.7)
(2.7)
By using the continuity method and the principle of contracting mappings, we can find the solutions
 (2.8)
(2.8)
where 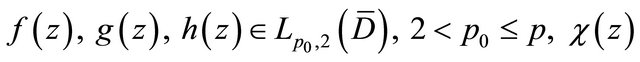
is a homeomorphism on  is a univalent analytic function, which conformally maps
is a univalent analytic function, which conformally maps  onto an
onto an  -connected circular domain
-connected circular domain , and
, and  is an analytic function in
is an analytic function in . We can verify that
. We can verify that  satisfy the estimates (2.2) and (2.3). Moreover noting that
satisfy the estimates (2.2) and (2.3). Moreover noting that  is a homeomorphic solution of the Beltrami complex Equation (2.7), which maps the circular domain
is a homeomorphic solution of the Beltrami complex Equation (2.7), which maps the circular domain  onto the circular domain
onto the circular domain  with the condition
with the condition  and
and 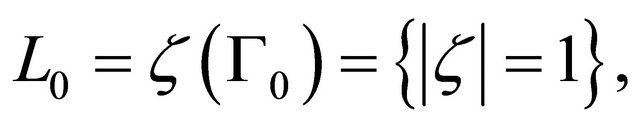 in accordance with the result in Lemma 2.1, Chapter 2, [3], we see that the estimate (2.4) is true.
in accordance with the result in Lemma 2.1, Chapter 2, [3], we see that the estimate (2.4) is true.
Now, we derive a priori estimates of solutions for Problem  and for Problem
and for Problem  for the complex Equation (1.1).
for the complex Equation (1.1).
Theorem 2.2. Under the same conditions as in Theorem 2.1, any solution  of Problem
of Problem  (or Problem
(or Problem ) for (1.1) satisfies the estimates
) for (1.1) satisfies the estimates
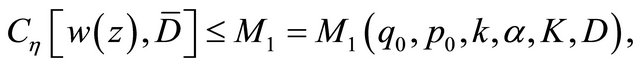 (2.9)
(2.9)
 (2.10)
(2.10)
where

are non-negative constants only dependent on  and
and  respectively.
respectively.
Proof. On the basis of Theorem 2.1, the solution  of Problem
of Problem  (or Problem
(or Problem ) can be expressed the formula as in (2.1), hence the boundary value problem
) can be expressed the formula as in (2.1), hence the boundary value problem  can be transformed into the boundary value problem (Problem
can be transformed into the boundary value problem (Problem ) for analytic functions
) for analytic functions
 (2.11)
(2.11)

(2.12)
 (2.13)
(2.13)
where

By (2.2)-(2.4), it can be seen that  satisfy the conditions
satisfy the conditions
 (2.14)
(2.14)
where  If we can prove that the solution
If we can prove that the solution  of Problem
of Problem satisfies the estimate
satisfies the estimate
 (2.15)
(2.15)
in which 


 then from the representation (2.1) of the solution
then from the representation (2.1) of the solution  and the estimates (2.2)-(2.4) and (2.15), the estimates (2.9) and (2.10) can be derived.
and the estimates (2.2)-(2.4) and (2.15), the estimates (2.9) and (2.10) can be derived.
It remains to prove that (2.15) holds. For this, we first verify the boundedness of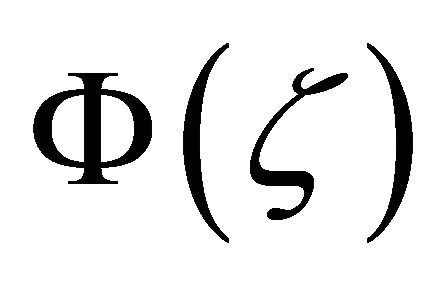 , i.e.
, i.e.
 (2.16)
(2.16)
Suppose that (2.16) is not true. Then there exist sequences of functions 
 satisfying the same conditions as
satisfying the same conditions as  which uniformly converge to
which uniformly converge to  on L respectively. For the solution
on L respectively. For the solution  of the boundary value problem (Problem
of the boundary value problem (Problem ) corresponding to
) corresponding to  we have
we have
 as
as  There is no harm in assuming that
There is no harm in assuming that  Obviously
Obviously  satisfies the boundary conditions
satisfies the boundary conditions
 (2.17)
(2.17)
 (2.18)
(2.18)
Applying the Schwarz formula, the Cauchy formula and the method of symmetric extension (see Theorem 1.4, Chapter 1, [3]), the estimates
(see Theorem 1.4, Chapter 1, [3]), the estimates
 (2.19)
(2.19)
can be obtained, where 
 . Thus we can select a subsequence of
. Thus we can select a subsequence of  which uniformly converge to an analytic function
which uniformly converge to an analytic function  in
in , and
, and 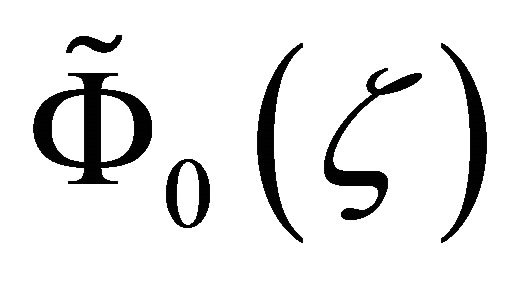 satisfies the homogeneous boundary conditions
satisfies the homogeneous boundary conditions
 (2.20)
(2.20)
 (2.21)
(2.21)
On the basis of the uniqueness theorem (see Theorem 2.4), we conclude that
(see Theorem 2.4), we conclude that  Howeverfrom
Howeverfrom  it follows that there exists a point
it follows that there exists a point  such that
such that  This contradiction proves that (2.16) holds. Afterwards using the method which leads from
This contradiction proves that (2.16) holds. Afterwards using the method which leads from  to (2.19), the estimate (2.15) can be derived.
to (2.19), the estimate (2.15) can be derived.
Similarly, we can verify that any solution  of Problem
of Problem  satisfies the estimates (2.9) and (2.10).
satisfies the estimates (2.9) and (2.10).
Theorem 2.3. Under the same conditions as in Theorem 2.1, any solution  of Problem
of Problem  (or Problem
(or Problem ) for (1.1) satisfies
) for (1.1) satisfies
 (2.22)
(2.22)
where  are as stated in Theorem 2.2,
are as stated in Theorem 2.2,

Proof. If  i.e.
i.e.  from Theorem 2.4, it follows that
from Theorem 2.4, it follows that . If
. If  it is easy to see that
it is easy to see that  satisfies the complex equation and boundary conditions
satisfies the complex equation and boundary conditions
 (2.23)
(2.23)
 (2.24)
(2.24)
 (2.25)
(2.25)
Noting that

and according to the proof of Theorem 2.2, we have
 (2.26)
(2.26)
From the above estimates, it immediately follows that (2.22) holds.
Next, we prove the uniqueness of solutions of Problem  and Problem
and Problem  for the complex Equation (1.1). For this, we need to add the following condition: For any continuous functions
for the complex Equation (1.1). For this, we need to add the following condition: For any continuous functions  on
on  and
and 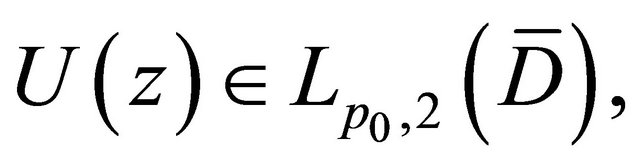 there is
there is
 (2.27)
(2.27)
where . When (1.1) is linear, (3.27) obviously holds.
. When (1.1) is linear, (3.27) obviously holds.
Theorem 2.4. If Condition C and (2.27) hold, then the solution of Problem  (or Problem
(or Problem ) for (1.1) is unique.
) for (1.1) is unique.
Proof. Let  be two solutions of Problem
be two solutions of Problem  for (1.1). By Condition
for (1.1). By Condition  and (2.27), we see that
and (2.27), we see that  is a solution of the following boundary value problem
is a solution of the following boundary value problem
 (2.28)
(2.28)
 (2.29)
(2.29)
 (2.30)
(2.30)
where

and  According to the representation (2.1), we have
According to the representation (2.1), we have
 (2.31)
(2.31)
where  are as stated in Theorem 2.1. It can be seen that the analytic function
are as stated in Theorem 2.1. It can be seen that the analytic function  satisfies the boundary conditions of Problem
satisfies the boundary conditions of Problem 
 (2.32)
(2.32)
 (2.33)
(2.33)
where  are as stated in (2.11)-(2.13). In accordance with Theorem 2.2, it can be derived that
are as stated in (2.11)-(2.13). In accordance with Theorem 2.2, it can be derived that 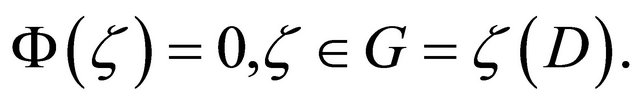 Hence,
Hence,
 i.e.
i.e. 
3. The Continuity Method of Solving Boundary Value Problem
Next, we discuss the modified Riemann-Hilbert boundary value problems (Problem  and Problem
and Problem ) for the nonlinear elliptic complex Equation (1.1) in the (N+1)-connected unbounded domain
) for the nonlinear elliptic complex Equation (1.1) in the (N+1)-connected unbounded domain  as stated in Section 1, here we use the Newton imbedding method of another form and give an error estimate, which is better than that as stated before. In the following, we only deal with Problem
as stated in Section 1, here we use the Newton imbedding method of another form and give an error estimate, which is better than that as stated before. In the following, we only deal with Problem , because by using the same method, Problem
, because by using the same method, Problem  can be discussed.
can be discussed.
Theorem 3.1. Suppose that the nonlinear elliptic Equation (1.1) satisfies Condition C and (1.6), (1.10), on . Then Problem
. Then Problem  for (1.1) has a solution
for (1.1) has a solution 
Proof We introduce the nonlinear elliptic complex equation with the parameter :
:
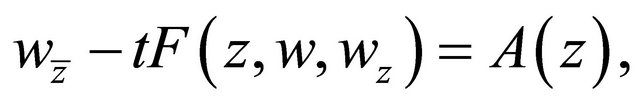 (3.1)
(3.1)
where  is any measurable function in
is any measurable function in  and
and  When
When , it is not difficult to see that there exists a unique solution
, it is not difficult to see that there exists a unique solution  of Problem
of Problem  for the complex Equation (3.1), which possesses the form
for the complex Equation (3.1), which possesses the form
 (3.2)
(3.2)
where  is an analytic function in
is an analytic function in  and satisfies the boundary conditions
and satisfies the boundary conditions
 (3.3)
(3.3)
 (3.4)
(3.4)
From Theorem Theorem 2.2, We see that

Suppose that when , Problem
, Problem  for the complex Equation (1.18) has a unique solution, we shall prove that there exists a neighborhood of
for the complex Equation (1.18) has a unique solution, we shall prove that there exists a neighborhood of
 so that for every
so that for every
 and any function
and any function  Problem
Problem  for (1.18) is solvable. In fact, the complex Equation (3.2) can be written in the form
for (1.18) is solvable. In fact, the complex Equation (3.2) can be written in the form
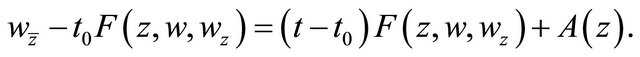 (3.5)
(3.5)
We arbitrarily select a function
 in particular
in particular
 on
on . Let
. Let  be replaced into the position of
be replaced into the position of  in the right hand side of (1.22). By Condition
in the right hand side of (1.22). By Condition , it is obvious that
, it is obvious that

Noting the (3.5) has a solution  Applying the successive iteration, we can find out a sequence of functions:
Applying the successive iteration, we can find out a sequence of functions:  which satisfy the complex equations
which satisfy the complex equations
 (3.6)
(3.6)
The difference of the above equations for  and n is as follows:
and n is as follows:
 (3.7)
(3.7)
From Condition , on
, on , it can be seen that
, it can be seen that


and

Moreover,  satisfies the homogeneous boundary conditions
satisfies the homogeneous boundary conditions
 (3.8)
(3.8)
 (3.9)
(3.9)
On the basis of Theorem 2.3, we have
 (3.10)
(3.10)
where 
 is as stated in (2.22). Provided
is as stated in (2.22). Provided  is small enough, so that
is small enough, so that
 it can be obtained that
it can be obtained that
 (3.11)
(3.11)
for every  Thus
Thus
 (3.12)
(3.12)
for  where
where  is a positive integer. This shows that
is a positive integer. This shows that  as
as  Following the completeness of the Banach space
Following the completeness of the Banach space
 there is a function
there is a function  such that when
such that when 

By Condition  and (1.6), (1.10), from the above formula it follows that
and (1.6), (1.10), from the above formula it follows that  is a solution of Problem
is a solution of Problem  for (3.5), i.e. (3.1) for
for (3.5), i.e. (3.1) for . It is easy to see that the positive constant
. It is easy to see that the positive constant  is independent of
is independent of . Hence from Problem
. Hence from Problem  for the complex Equation (3.1) with
for the complex Equation (3.1) with  is solvable, we can derive that when
is solvable, we can derive that when , Problem
, Problem  for (3.1) are solvable, especially Problem
for (3.1) are solvable, especially Problem  for (3.2) with
for (3.2) with  and
and , namely Problem
, namely Problem  for (1.1) has a unique solution.
for (1.1) has a unique solution.
4. Error Estimates of Approximate Solutions for Boundary Value Problem
In this section, we shall introduce an error estimate of the above approximate solutions of the boundary value problem and can give the following error estimate of the approximate solutions.
Theorem 4.1 Let  be a solution of Problem
be a solution of Problem  for the complex Equation (1.1) satisfying Condition
for the complex Equation (1.1) satisfying Condition  and (1.6), (1.10) on
and (1.6), (1.10) on , and
, and  be its approximation as stated in the proof of Theorem 2.2 with
be its approximation as stated in the proof of Theorem 2.2 with 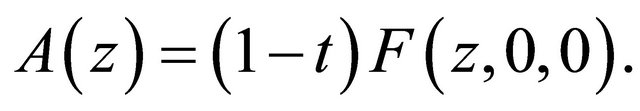 Then we have the following error estimate
Then we have the following error estimate
 (4.1)
(4.1)
where 

 and
and  are constants in (1.3), (1.6) and (1.10).
are constants in (1.3), (1.6) and (1.10).
Proof From (1.1) and (2.23) with  , we have
, we have
 (4.2)
(4.2)
It is clear that  satisfies the homogeneous boundary conditions
satisfies the homogeneous boundary conditions
 (4.3)
(4.3)
 (4.4)
(4.4)
Noting that
 satisfy
satisfy
 , and
, and


and according to Theorem 2.2, it can be concluded

(4.5)
where  and
and
 (4.6)
(4.6)
where  are non-negative constants as stated in (1.3), (1.6) and (1.10). From (4.5) and (4.6), it follows
are non-negative constants as stated in (1.3), (1.6) and (1.10). From (4.5) and (4.6), it follows

where  and we choose that
and we choose that  is the solution of Problem
is the solution of Problem  for (2.22) with
for (2.22) with  and
and  Due to
Due to  is a solution of Problem
is a solution of Problem  for the complex equation
for the complex equation
 (4.7)
(4.7)
hence
 (4.8)
(4.8)
Finally, we obtain

(4.9)
this shows that (4.1) holds. If the positive constant  is small enough, so that when
is small enough, so that when 
 is sufficiently large and
is sufficiently large and  is close to 1, then the right hand side becomes small.
is close to 1, then the right hand side becomes small.