Kruskal Coordinates and Mass of Schwarzschild Black Holes: No Finite Mass Black Hole at All ()
1. Introduction
The concept of Black Holes (BHs) is one of the most important plinths of modern physics and astrophysics. As is well known, the basic concept of BHs originally arose due to Laplace, more than 200 years ago, in the cradle of Newtonian gravitation, where the mass of a body remains fixed during collapse. In General Theory of Relativity (GTR), the gravitational mass is less than the baryonic mass . Further, as the body contracts and emits radiation
. Further, as the body contracts and emits radiation 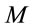 keeps on decreasing progressively along with
keeps on decreasing progressively along with  [1]. Thus, given an initial gravitational mass
[1]. Thus, given an initial gravitational mass , one can not predict with certainty the value of
, one can not predict with certainty the value of 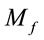 when we would have
when we would have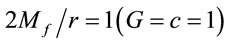 . Neither are the values of
. Neither are the values of ,
, 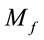 and
and  related by any combination of fundamental constants though, it is generally assumed that
related by any combination of fundamental constants though, it is generally assumed that . Ideally, one should solve the Einstein equations analytically to fix the value of
. Ideally, one should solve the Einstein equations analytically to fix the value of  for a given initial values of
for a given initial values of 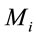 and
and  for a realistic equation of state (EOS) and energy transport properties [2,3]. However even when one does away with the EOS by assuming the matter to behave like a dust,
for a realistic equation of state (EOS) and energy transport properties [2,3]. However even when one does away with the EOS by assuming the matter to behave like a dust,  , one does not obtain any unique solution if the dust is inhomogeneous. Depending on the various initial conditions and assumptions (like self-similarity) employed one may end up finding either a BH or a “naked singularity” [4]. By further assuming the dust to be homogeneous Oppenheimer and Snyder (OS) [5] found an asymptotic solution of the problem by approximating Equation (36) of their paper [2,3]. The region exterior to the event horizon
, one does not obtain any unique solution if the dust is inhomogeneous. Depending on the various initial conditions and assumptions (like self-similarity) employed one may end up finding either a BH or a “naked singularity” [4]. By further assuming the dust to be homogeneous Oppenheimer and Snyder (OS) [5] found an asymptotic solution of the problem by approximating Equation (36) of their paper [2,3]. The region exterior to the event horizon 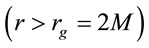 can be described by the Schwarzschild coordinates
can be described by the Schwarzschild coordinates  and
and  [6,7]:
[6,7]:
 (1)
(1)
where ,
, 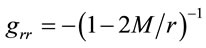 ,
,  , and
, and . Here, we are working with a spacetime signature of
. Here, we are working with a spacetime signature of  and
and  has a distinct physical significance as the invariant circumference radius. For
has a distinct physical significance as the invariant circumference radius. For , the worldline of a free falling radial material particle is indeed timelike
, the worldline of a free falling radial material particle is indeed timelike  and the metric coefficients have the right signature,
and the metric coefficients have the right signature,
 But at
But at 
 blows up and as
blows up and as , the
, the  and
and 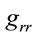 suddenly exchange their signatures though the signatures of
suddenly exchange their signatures though the signatures of  and
and  remain unchanged. This is interpreted by saying that, inside the event horizon,
remain unchanged. This is interpreted by saying that, inside the event horizon,  becomes “time like” and
becomes “time like” and  becomes “spacelike”. However, we see that actually
becomes “spacelike”. However, we see that actually  continues to retain, atleast partially, its spacelike character by continuing to be the “invariant circumference radius”. Also, note that, if physically meaningful quantities like the Rimennian curvature components behaved like
continues to retain, atleast partially, its spacelike character by continuing to be the “invariant circumference radius”. Also, note that, if physically meaningful quantities like the Rimennian curvature components behaved like  outside the EH, they continue to behave in a similar manner, and not like
outside the EH, they continue to behave in a similar manner, and not like  inside the EH. And it should be borne in mind here that by a fresh relabelling or by any other means, the curvature components can not be made to assume the form
inside the EH. And it should be borne in mind here that by a fresh relabelling or by any other means, the curvature components can not be made to assume the form . One particular reason for this is that, we would see later that, inside the EH, we have
. One particular reason for this is that, we would see later that, inside the EH, we have 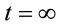 while, of course, the value of
while, of course, the value of  remains finite. Thus it may not actually be justified to conclude that
remains finite. Thus it may not actually be justified to conclude that  becomes the “timelike coordinate” inside the EH even though
becomes the “timelike coordinate” inside the EH even though 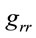 changes its sign.
changes its sign.
So far, it has not been possible to resolve this enigma of the duality in the behaviour of  for
for , and the present paper intends to attend to this problem. Since Kruskal coordinates
, and the present paper intends to attend to this problem. Since Kruskal coordinates  are believed to properly chart the SBH spacetime, it is imperative that, one studies the properties of these coordinates. In a recent paper (Pap. I) we found that the Kruskal derivative
are believed to properly chart the SBH spacetime, it is imperative that, one studies the properties of these coordinates. In a recent paper (Pap. I) we found that the Kruskal derivative  at the EH [8]. However, this derivative can be obtained from various directions, and in some cases,
at the EH [8]. However, this derivative can be obtained from various directions, and in some cases,  may assume a
may assume a  form as
form as . Here we would like to closely examine such cases. Eventually, it would be found that, for self-consistency, one must have
. Here we would like to closely examine such cases. Eventually, it would be found that, for self-consistency, one must have  at
at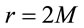 . This result would suggest, that for a neutral point mass, the integration constant appearing the SBH solution is
. This result would suggest, that for a neutral point mass, the integration constant appearing the SBH solution is . Then, as we will soon see, the Kruskal coordinates implicitly involve division by zero, and which explains various oddities associated with them. We would also take note of the objections associated with the Kruskal coordinates by some other authors.
. Then, as we will soon see, the Kruskal coordinates implicitly involve division by zero, and which explains various oddities associated with them. We would also take note of the objections associated with the Kruskal coordinates by some other authors.
2. Kruskal Coordinates
Although 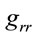 blows up at
blows up at , as mentioned before, the curvature components of the Rimennian tensor appear to behave (under the assumption M > 0) perfectly normally at
, as mentioned before, the curvature components of the Rimennian tensor appear to behave (under the assumption M > 0) perfectly normally at . Further, the determinant of the metric coefficients continues to be negative and finite
. Further, the determinant of the metric coefficients continues to be negative and finite . Such realizations gave rise to the idea that the Schwarzschild coordinate system suffers from a “coordinate singularity” at the event horizon and must be replaced by some other well behaved coordinate system. It is only in 1960 that Kruskal and Szekeres [9,10] discovered a one-piece coordinate system which can describe both the interior and exterior regions of a BH. They achieved this by means of the following coordinate transformation for the exterior region (Sector 1):
. Such realizations gave rise to the idea that the Schwarzschild coordinate system suffers from a “coordinate singularity” at the event horizon and must be replaced by some other well behaved coordinate system. It is only in 1960 that Kruskal and Szekeres [9,10] discovered a one-piece coordinate system which can describe both the interior and exterior regions of a BH. They achieved this by means of the following coordinate transformation for the exterior region (Sector 1):
 (2)
(2)
where
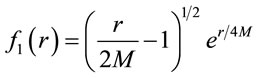 (3)
(3)
It would be profitable to note that
 (4)
(4)
And for the region interior to the horizon (Sector 2), we have
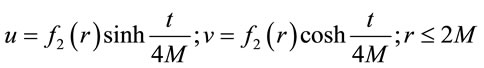 (5)
(5)
where
 (6)
(6)
and
 (7)
(7)
Note these are the only coordinates which involve  in the denominator. Given our adopted signature of spacetime
in the denominator. Given our adopted signature of spacetime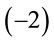 , in terms of
, in terms of  and
and , the metric for the entire spacetime is
, the metric for the entire spacetime is
 (8)
(8)
The metric coefficients are apparently regular everywhere except at the intrinsic singularity . Note that, the angular part of the metric remains unchanged by such transformations and
. Note that, the angular part of the metric remains unchanged by such transformations and  continues to signal its intrinsic spacelike nature. In either region we have
continues to signal its intrinsic spacelike nature. In either region we have
 (9)
(9)
so that
 (10)
(10)
 (11)
(11)
and
 (12)
(12)
So, very strangely, the  point corresponds to not one but two conditions!
point corresponds to not one but two conditions!
 (13)
(13)
Here, one point needs to be hardly overemphasized; astronomical observations and experiments actually conform to the idea that atleast far from massive bodies or even BH Candidates (BHC), the spacetime is well described by the  coordinate system. In fact, although in the (normal) physical spacetime, in a spherically symmetric spatial geometry (as defined by the implications of
coordinate system. In fact, although in the (normal) physical spacetime, in a spherically symmetric spatial geometry (as defined by the implications of  as an “invariant circumference radius”), the physical singularity corresponds to a mathematical point, in the Kruskal world view, this central singularity corresponds to a pair of hyperbolas in the
as an “invariant circumference radius”), the physical singularity corresponds to a mathematical point, in the Kruskal world view, this central singularity corresponds to a pair of hyperbolas in the 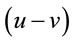 plane. While the “+ve” sign of equation corresponds to the central BH singularity, the “−ve” sign corresponds to the singularity inside a so-called White Hole which may spew out mass-energy spontaneously in “our universe” [6,7]. The white hole singularity belongs to “other universe” whose presence is suggested by the fact that the Kruskal metric remains unaffected by the following additional transformations:
plane. While the “+ve” sign of equation corresponds to the central BH singularity, the “−ve” sign corresponds to the singularity inside a so-called White Hole which may spew out mass-energy spontaneously in “our universe” [6,7]. The white hole singularity belongs to “other universe” whose presence is suggested by the fact that the Kruskal metric remains unaffected by the following additional transformations:
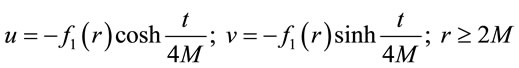 (14)
(14)
defining Sector (III) and
 (15)
(15)
defining Sector 4. Thus not only does the region interior to the EH correspond to two different universes (Sectors 2 and 4), but the structure of the physical spacetime outside the EH, too, effectively corresponds to two universes (Sectors 1 and 3). Hence, if there would be  separate BHs, as per the Kruskal prescription, there would be
separate BHs, as per the Kruskal prescription, there would be 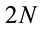 disconnected physically weird universes describing different wormholes and other universes. Hence if a massive star would indeed collapse to form BH in the universe we live, other universes would be instantly born!
disconnected physically weird universes describing different wormholes and other universes. Hence if a massive star would indeed collapse to form BH in the universe we live, other universes would be instantly born!
3. Kruskal Derivative
The aim of this paper is to explicitly verify whether the (radial) geodesics of material particles are indeed timelike at the EH, which they must be if this idea of a finite mass Schwarzschild BH is physically correct. First note that if the test particle is released from rest at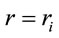 , then the conserved mass-energy per unit rest mass
, then the conserved mass-energy per unit rest mass  is given by
is given by
 (16)
(16)
Note, from various considerations, in Pap. I [8], we have already found that, at the EH, one should have
 (17)
(17)
Armed with this value of , we are in a position now to complete our task by rewriting the radial part of the Kruskal metric
, we are in a position now to complete our task by rewriting the radial part of the Kruskal metric as
as
 (18)
(18)
or,
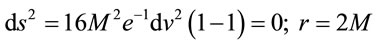 (19)
(19)
This implies that although the metric coefficients can be made to appear regular, the radial geodesic of a material particle would become null at the event horizon of a finite mass BH in contravention of the basic premises of GTR! Therefore GTR must not allow occurrence of any EH at all [2,3]!
In fact this result could have been easily anticipated by studying the limiting behaviour of the SBH metric in Schwarzschild coordinates too (even if one would assume that Schwarzschild coordinates break down at exact ). Using the vacuum Schwarzschild metric, for a radial geodesic in, one finds that find that [2,3]
). Using the vacuum Schwarzschild metric, for a radial geodesic in, one finds that find that [2,3]
 (20)
(20)
i.e.,
 (21)
(21)
But since
 (22)
(22)
for a radial geodesic, one eventually finds that
 (23)
(23)
Note that for a photon, 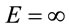 , and the foregoing equation correctly shows that
, and the foregoing equation correctly shows that . Also, for a material particle with
. Also, for a material particle with , it shows that indeed
, it shows that indeed  as long as
as long as . However even for a material particle worldline,
. However even for a material particle worldline,
 (24)
(24)
irrespective of the value of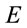 .
.
Therefore, the radial geodesic of a material particle in the Schwarzschild metric would become unphysically null  in case the particle would arrive at the EH. It may be noted here that though
in case the particle would arrive at the EH. It may be noted here that though , by definition
, by definition  is an infinetisimal quantity. And since
is an infinetisimal quantity. And since  is an invariant, its limiting value must not depend on the coordinates used. Accordingly, it is natural that Kruskal coordinates too should lead to
is an invariant, its limiting value must not depend on the coordinates used. Accordingly, it is natural that Kruskal coordinates too should lead to  as
as .
.
Note,  can be obtained from several approaches, and in Pap. I, we found that
can be obtained from several approaches, and in Pap. I, we found that  form in certain cases. Accordingly, let us evaluate
form in certain cases. Accordingly, let us evaluate 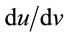 for such apparent
for such apparent  cases more carefully.
cases more carefully.
3.1. 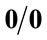 Form of the Kruskal Derivative
Form of the Kruskal Derivative
First let us define a quantity
 (25)
(25)
In Pap. I [2,3,8], by the brute direct approach, we found that
 (26)
(26)
To evaluate this derivative very carefully, close to the EH, let us first write
 . (27)
. (27)
Clearly, the value of  depends on whether
depends on whether  or
or , and let us first consider the former case:
, and let us first consider the former case:
3.2.  Case
Case
When , we have
, we have
 . (28)
. (28)
And thus close to the EH,
 . (29)
. (29)
For the positive sign of , as
, as , one finds
, one finds
 . (30)
. (30)
While for the negative sign of , one has
, one has
 . (31)
. (31)
Thus, for ,
,  as obtained in Pap I.
as obtained in Pap I.
3.3.  Case
Case
For , close to the EH, one has
, close to the EH, one has
 (32)
(32)
and
 (33)
(33)
where
 . (34)
. (34)
Simultaneously from (9), one finds that
 (35)
(35)
so that
 (36)
(36)
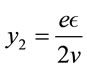 . (37)
. (37)
Thus, one has  sets of expressions for the value of
sets of expressions for the value of  at
at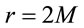 . And as we retain terms only upto first order of
. And as we retain terms only upto first order of , and further let
, and further let  whenever appropriate, from (26) we obtain:
whenever appropriate, from (26) we obtain:
1) 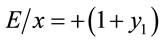 and
and 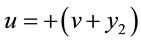
 (38)
(38)
By using the forms of  and
and , the above expression can be seen as
, the above expression can be seen as
 (39)
(39)
If , then one will have
, then one will have . But, if one will have
. But, if one will have , then, once again
, then, once again
 (40)
(40)
2)  and
and 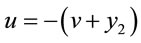
 (41)
(41)
Again, by using the forms of  and
and , the above expression can be seen as
, the above expression can be seen as
 (42)
(42)
If , then one will have
, then one will have . But, if one will have
. But, if one will have , then, once again
, then, once again
 (43)
(43)
3)  and
and 
 (44)
(44)
4)  and
and 
 (45)
(45)
Thus when we consider  and
and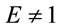 , we obtain self-contradictory and strange results. Apparently the cases 1) & 2) suggest that
, we obtain self-contradictory and strange results. Apparently the cases 1) & 2) suggest that  provided
provided 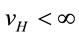 so that
so that  even as
even as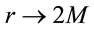 . Note that
. Note that  is an invariant, and thus such a result would be in contradiction with Equation (23) which shows that
is an invariant, and thus such a result would be in contradiction with Equation (23) which shows that  as
as  irrespective of the value of
irrespective of the value of . Indeed the hope that
. Indeed the hope that 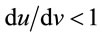 is belied in cases 3) & 4), which yield
is belied in cases 3) & 4), which yield 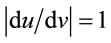 as before. And therefore, for a graceful exit from such a self-contradiction, one must accept that
as before. And therefore, for a graceful exit from such a self-contradiction, one must accept that 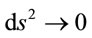 as
as  whose physical interpretation is
whose physical interpretation is  for a point particle.
for a point particle.
4. Interpretation
In view of such inconsistencies for  and
and  case, it appears that the presumption,
case, it appears that the presumption,  , on which the BH paradigm is based is incorrect. And even if we would momentarily accept this incorrect presumption, we would have to confront with the result that as the EH would be reached,
, on which the BH paradigm is based is incorrect. And even if we would momentarily accept this incorrect presumption, we would have to confront with the result that as the EH would be reached,  , i.e., geodesic would become lightlike. But this possibility is inconsistent with the BH paradigm where the EH is a regular region of spacetime and where the geodesic of a material particle must be timelike, i.e.,
, i.e., geodesic would become lightlike. But this possibility is inconsistent with the BH paradigm where the EH is a regular region of spacetime and where the geodesic of a material particle must be timelike, i.e., . Since
. Since  is an invariant, we can not blame the coordinate system to be faulty for such an inconsistency. So we must reject the presumption that a neutral point particle appearing in the vacuum SBH solution has a finite gravitational mass.
is an invariant, we can not blame the coordinate system to be faulty for such an inconsistency. So we must reject the presumption that a neutral point particle appearing in the vacuum SBH solution has a finite gravitational mass.
Therefore, clearly, for self-consistency, as far as a point mass is concerned (but not necessarily for an extended object like the Sun), one should have only . And since,
. And since, 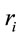 can very much be finite, it appears from Equation (16) that, for a neutral point mass or a SBH, one must have
can very much be finite, it appears from Equation (16) that, for a neutral point mass or a SBH, one must have .
.
For the SBH, there is only one spacetime singulatity which is at . Therefore, the EH and the true physical singularity must be the same:
. Therefore, the EH and the true physical singularity must be the same:
 (46)
(46)
And thus for the true SBH, one must have
 (47)
(47)
Irrespective of the above interpretation, the very fact the radial geodesic would turn lightlike if it would hit the EH means that the EH is no regular region of the spactime; on the other hand, the EH must be a spacetime singularity where the “once timelike always timelike” mathematical rule would break down. This is similar to the special relativistic situation where a test particle having a timelike geodesic would turn lightlike if there would be an accelerator of infinite capacity which would push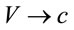 . In contrast, if finite mass SBHs would really have been allowed, one should have had
. In contrast, if finite mass SBHs would really have been allowed, one should have had  irrespective of the value of
irrespective of the value of  and irrespective of the coordinates employed. Indeed, the occurrence of
and irrespective of the coordinates employed. Indeed, the occurrence of  as
as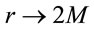 , proves in a coordinate independent manner that for any physically meaningful definition of 3-speed
, proves in a coordinate independent manner that for any physically meaningful definition of 3-speed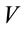 , one must have
, one must have  as
as  [2,3] irrespective of the coordinates used. The latter fact was even acknowledged by Crawford & Tereno [11] after initially denying it:
[2,3] irrespective of the coordinates used. The latter fact was even acknowledged by Crawford & Tereno [11] after initially denying it:
“Since this is an unacceptable result and we know that the Schwarzschild coordinate system is not suitable for describing the manifold at  it is rather tempting to blame the coordinate system for this malfunction. But we should ask first, could it be possible to find a coordinate system that does not have this defect? The answer is obviously no, since the result is independent of the choice of coordinates, ··· Indeed, even if we use a coordinate system that has no difficulties at
it is rather tempting to blame the coordinate system for this malfunction. But we should ask first, could it be possible to find a coordinate system that does not have this defect? The answer is obviously no, since the result is independent of the choice of coordinates, ··· Indeed, even if we use a coordinate system that has no difficulties at , like the advanced Eddington-Finkelstein coordinates, we would still end up with the same result
, like the advanced Eddington-Finkelstein coordinates, we would still end up with the same result  as
as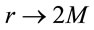 .”
.”
However, yet, to bypass this fact, they demanded that the speed of one infalling particle/observer having  must be measured by another infalling particle/ observer having
must be measured by another infalling particle/ observer having  [11]. This essentially means that to see whether a speeding car is violating some speed limit or not, the traffic inspector too must travel alongside the car rather than sit at the checkpost! By adopting this strange prescription for checking speed, they found that, the relative 3-speed of the infalling particles, with respect to each other, is given by[11]
[11]. This essentially means that to see whether a speeding car is violating some speed limit or not, the traffic inspector too must travel alongside the car rather than sit at the checkpost! By adopting this strange prescription for checking speed, they found that, the relative 3-speed of the infalling particles, with respect to each other, is given by[11]
 (48)
(48)
where , (note, in different context, we also use
, (note, in different context, we also use ). And at the EH, this yields
). And at the EH, this yields
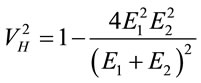 (49)
(49)
sothat, apparently,  if
if . In particular, if
. In particular, if , one will have
, one will have ; i.e., the observer/particle would conclude that he/she is at rest at the EH. This is a profound self-contradiction because Crawford & Tereno starts with the premises that the concept of staticity vanishes at the EH and below it. In fact, in GR, the local speed must indeed be measured locally; i.e., the observer and the test particle must be at the same spatial location. In other words, the two infalling particles must have the same comoving proper time at a given spatial position. For a free fall, this can be ensured everwhere, only when the two particles/observers have the same initial conditions, i.e.,
; i.e., the observer/particle would conclude that he/she is at rest at the EH. This is a profound self-contradiction because Crawford & Tereno starts with the premises that the concept of staticity vanishes at the EH and below it. In fact, in GR, the local speed must indeed be measured locally; i.e., the observer and the test particle must be at the same spatial location. In other words, the two infalling particles must have the same comoving proper time at a given spatial position. For a free fall, this can be ensured everwhere, only when the two particles/observers have the same initial conditions, i.e.,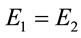 . Thus as per Crawford & Tereno, the observer must fall along with the test particle side by side! And when this is so, one must have
. Thus as per Crawford & Tereno, the observer must fall along with the test particle side by side! And when this is so, one must have  everywhere! This is like the situation, when the speeding car driver dictates that the traffic inspector must measure his speed by sitting in the same car, in the adjacent seat [3]! With reference to Equation (48), even if one would assume
everywhere! This is like the situation, when the speeding car driver dictates that the traffic inspector must measure his speed by sitting in the same car, in the adjacent seat [3]! With reference to Equation (48), even if one would assume , and
, and , at
, at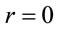 , one will have
, one will have  because
because
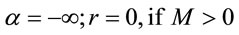 (50)
(50)
Therefore, following Crawford & Terneno prescription, even at the central singularity
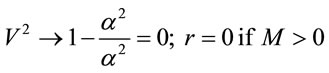 (51)
(51)
And this above absurdity can be removed by considering that at the EH,  so that
so that .
.
Unfortunately, the same physically nonsense ansatz for speed measurement has recently been adopted by another author too [12]. He [12] has attempted to include angular momentum in the ansatz of Crawford & Tereno. For certain conditions, he indeed finds that: “So even if it had not go to r = 0 the particle is seen to move with the velocity of light.” But he proceeds by ignoring this redsignal. He again finds, “At large value of angular momentum the velocity approaches that of 1” (p. 12). But strangely he opines the  situation to be justified!
situation to be justified!
Even when one considers accretion of a perfect fluid onto a SBH [13]“calculations show that the total velocity  tends toward
tends toward  as
as , which is in accordance with expectations” (see p. 9) [13].
, which is in accordance with expectations” (see p. 9) [13].
Unfortunately, these authors fail to realize here that ocurrence of  is not allowed in GR because this implies
is not allowed in GR because this implies  for the accreting fluid! On the other hand, such results actually imply that astrophysical and all other so-called BHs must be something else [14,15].
for the accreting fluid! On the other hand, such results actually imply that astrophysical and all other so-called BHs must be something else [14,15].
Let us also ponder, how a test particle can be prevented from hitting the EH ever in order that its timelike geodesic remains so. The test particle would never arrive at the EH, if the associated proper time would be infinite: i.e.,
 (52)
(52)
Clearly this demands that the gravitational mass of the SBH .
.
Note, when one incorrectly presumes a BH with , one arrives at a fundamental self-contraction: As per the distant inertial observer (who actually does the experiment), the test particle can approach the EH only asymptotically, and can neither ever reach it or penetrate it. On the other hand, as per the free falling observer, he not only arrives at the EH but can reach the central singularity too. Such a dichotomy is against the principle of general covariance by which ultimate physical results must not depend on choice of coordinates, and must be same for all observers. And this fundamental inconsistency gets resolved only when one realizes that for a BH,
, one arrives at a fundamental self-contraction: As per the distant inertial observer (who actually does the experiment), the test particle can approach the EH only asymptotically, and can neither ever reach it or penetrate it. On the other hand, as per the free falling observer, he not only arrives at the EH but can reach the central singularity too. Such a dichotomy is against the principle of general covariance by which ultimate physical results must not depend on choice of coordinates, and must be same for all observers. And this fundamental inconsistency gets resolved only when one realizes that for a BH,  , so that both
, so that both .
.
Also note, unlike the case of Newtonian gravity, in GTR,  state need not correspond to a configuration with zero baryonic mass. The
state need not correspond to a configuration with zero baryonic mass. The  state is simply one in which the negative gravitational energy exactly offsets the positive energy associated with
state is simply one in which the negative gravitational energy exactly offsets the positive energy associated with  and internal energy, and may indeed represent a physical singularity with infinite energy density and tidal acceleration.
and internal energy, and may indeed represent a physical singularity with infinite energy density and tidal acceleration.
On the other hand, since in Newtonian gravity, the negative self-gravitational energy does not offset the bare mass, a point particle can have arbitrary large positive mass; and hence, the concept of a finite mass BH fits better in a Newtonian context.
5. Discussions
Even the authors who, in a desperate bid to save the black hole paradigm, invent almost ridiculous definition of “free fall speed” by which an infalling particle has  even at the central singularity, were forced to conclude that [16]
even at the central singularity, were forced to conclude that [16]
“The solutions that do away with the interior singularity and the event horizon, although interesting in themselves, sweep the inherent conceptual difficulties of black holes under the rug. In concluding, we note that the interior structure of realistic black holes have not been satisfactorily determined, and are still open to considerable debate.” (Emphasis by the author).
If the staple topic of discussion of lakhs of textbooks and may be millions of articles and news reports have not been “satisfactorily determined” in almost 100 years, it is certain that, the paradigm itself is unphysical and faulty.
On the other hand, with the direct result that  for the SBH, the entire conundrum of “Schwarzschild singularity”, swapping of spatial and temporal characters by
for the SBH, the entire conundrum of “Schwarzschild singularity”, swapping of spatial and temporal characters by  and
and  inside the event horizon (when the angular part of all metrics suggest that
inside the event horizon (when the angular part of all metrics suggest that  has a spacelike character even within the horizon), “White Holes” and “Other Universes” get resolved. Here we recall the wise comments of Rosen [17].
has a spacelike character even within the horizon), “White Holes” and “Other Universes” get resolved. Here we recall the wise comments of Rosen [17].
“So that in this region  is timelike and
is timelike and  is spacelike. However, this is an impossible situation, for we have seen that
is spacelike. However, this is an impossible situation, for we have seen that  defined in terms of the circumference of a circle so that
defined in terms of the circumference of a circle so that  is spacelike, and we are therefore faced with a contradiction. We must conclude that the portion of space corresponding to
is spacelike, and we are therefore faced with a contradiction. We must conclude that the portion of space corresponding to  is nonphysical. This is a situation which a coordinate transformation even one which removes a singularity can not change. What it means is that the surface
is nonphysical. This is a situation which a coordinate transformation even one which removes a singularity can not change. What it means is that the surface  represents the boundary of physical space and should be regarded as an impenetrable barrier for particles and light rays.”
represents the boundary of physical space and should be regarded as an impenetrable barrier for particles and light rays.”
This idea of Rosen is also in accordance with the idea of Einstein that the Schwarzschild type singularity is unphysical and can not occur for realistic cases [18].
And this paper indeed shows that in order that the radial worldlines of free falling material particles do not become null at a mere coordinate singularity, Nature (GTR) refuses to have any spacetime within the EH. And this unphysical happening is of course avoided when we realize that 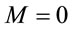 and there is no additional spacetime between the EH and the central singularity.
and there is no additional spacetime between the EH and the central singularity.
5.1. Nature of Black Hole Candidates
Some readers would however ignore this cogent result that  for a true BH, by arguing that there are massive compact astrophysical objects and which must be BHs. Such an argument would be based on the fact that cold self-gravitating objects cannot be more massive that few solar masses
for a true BH, by arguing that there are massive compact astrophysical objects and which must be BHs. Such an argument would be based on the fact that cold self-gravitating objects cannot be more massive that few solar masses in view of Chandrasekhar and Tolman OppenheimerVolkoff (TOV) limits.
in view of Chandrasekhar and Tolman OppenheimerVolkoff (TOV) limits.
Note the concepts of Chandrasekhar or TOV are based on degenerate fermions at temperature . Therefore, they are irrelevant for objects which are extremely hot and not supported by mere cold degenerate pressure. For instance there known hot stars with masses as large
. Therefore, they are irrelevant for objects which are extremely hot and not supported by mere cold degenerate pressure. For instance there known hot stars with masses as large , and in principle, there could be radiation pressure supported stars (RPSSs) with masses as large as
, and in principle, there could be radiation pressure supported stars (RPSSs) with masses as large as  [7,19]. Such quasi-Newtonian RPSSs however have a lower mass limit of
[7,19]. Such quasi-Newtonian RPSSs however have a lower mass limit of 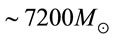 and they are considered as strictly static solutions. Accordingly, they must obey the Buchdahl limit
and they are considered as strictly static solutions. Accordingly, they must obey the Buchdahl limit 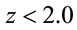 [20]. Indeed such quasi-Newtonian supermassive stars in principle may have a surface gravitational red-shift
[20]. Indeed such quasi-Newtonian supermassive stars in principle may have a surface gravitational red-shift 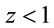 [7,16]. In contrast, in principle there could be quasi-static extremely relativistic radiation pressure supported stars with
[7,16]. In contrast, in principle there could be quasi-static extremely relativistic radiation pressure supported stars with  (RRPSSs) and no lower mass limit as well [21-23]. It may be recalled that it was Hoyle & Folwler who first suggested that the central compact objects of quasars could be hot quasi-Newtonian RPSSs [24,25]. They however conceived these RPSSs as strictly static ones whose source of internal energy and pressure is due to central nuclear burning; i.e., they ignored the fact quasistatic RPSSs can generate internal energy simply by virtue of quasi-static gravitational contraction [21-23].
(RRPSSs) and no lower mass limit as well [21-23]. It may be recalled that it was Hoyle & Folwler who first suggested that the central compact objects of quasars could be hot quasi-Newtonian RPSSs [24,25]. They however conceived these RPSSs as strictly static ones whose source of internal energy and pressure is due to central nuclear burning; i.e., they ignored the fact quasistatic RPSSs can generate internal energy simply by virtue of quasi-static gravitational contraction [21-23].
In fact there are several other alternative BH models and all of which may have  and arbitrary high mass [26]. It is also often argued that, the observed BH candidates must be true BHs, because, radio and X-ray observations might have probed them down to few Schwarzschild radii. Clearly, in view of the existence of several BH candidates with
and arbitrary high mass [26]. It is also often argued that, the observed BH candidates must be true BHs, because, radio and X-ray observations might have probed them down to few Schwarzschild radii. Clearly, in view of the existence of several BH candidates with  and
and , such astronomical observations have not at all confirmed that the so-called BH candidates are true BHs. Further it is hoped that the Event Horizon telescope would actually image the EH of the BH candidates. In reality, because of strong gravitational lensing near an ultracompact object, the distantly observed image would always be larger than the photon sphere having
, such astronomical observations have not at all confirmed that the so-called BH candidates are true BHs. Further it is hoped that the Event Horizon telescope would actually image the EH of the BH candidates. In reality, because of strong gravitational lensing near an ultracompact object, the distantly observed image would always be larger than the photon sphere having  and
and . Thus no telescope would ever be able to detect the fictitious EH. And of course, by definition, it is not possible to detect the EH “from which nothing, not even light can escape”.
. Thus no telescope would ever be able to detect the fictitious EH. And of course, by definition, it is not possible to detect the EH “from which nothing, not even light can escape”.
Hence there is no observational proof which can mysteriously upstage the exact result 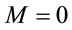 obtained here.
obtained here.
5.2. Gravitational Collapse
Some readers may argue that there is an exact GR solution by Oppenheimer & Snyder (OS) which shows that sufficiently massive objects must undergo gravitational collapse to form BHs, and hence the integration constant appearing in SBH or Kruskal solution cannot be zero. The OS solution assumes the collapsing object to be homogeneous when no self-gravitating object can be strictly homogeneous [27]. Further, it assumes the collapsing matter to be “dust with no pressure at all; . If the homogeneity assumption would be dropped, even the fictitious pressure-less dust solutions often lead to EH less Naked Singularity rather than a BH [4]. And it has recently been shown that the OS solution, though may appear to be mathematically correct, has only a symbolical value because it actually corresponds to zero matter density
. If the homogeneity assumption would be dropped, even the fictitious pressure-less dust solutions often lead to EH less Naked Singularity rather than a BH [4]. And it has recently been shown that the OS solution, though may appear to be mathematically correct, has only a symbolical value because it actually corresponds to zero matter density  [28]. This is expected because exact zero pressure, can be achieved only mathematically when
[28]. This is expected because exact zero pressure, can be achieved only mathematically when  too. Thus, in reality, there is no exact GR solution which indicates formation of finite mass BHs. Given the physical fact that the strict
too. Thus, in reality, there is no exact GR solution which indicates formation of finite mass BHs. Given the physical fact that the strict  condition implies
condition implies , many of the examples of naked singularity formation in GR collapse are equally fictitious. Even if one would ingore the proof that for a dust
, many of the examples of naked singularity formation in GR collapse are equally fictitious. Even if one would ingore the proof that for a dust , a critical analysis of Oppenheimer-Snyder collapse made in the Schwarzschild frame has revealed that, in reality, OS collapse does not result in any event horizon, any trapped surface or any finite mass black hole [29]. And this profound result is based on the simple mathematical fact that the argument of a logarithmic function must be positive definite [29].
, a critical analysis of Oppenheimer-Snyder collapse made in the Schwarzschild frame has revealed that, in reality, OS collapse does not result in any event horizon, any trapped surface or any finite mass black hole [29]. And this profound result is based on the simple mathematical fact that the argument of a logarithmic function must be positive definite [29].
On the other hand, realistic gravitational collapse always involves pressure gradient, heat and radiation transport [1-3,21-23]. When such complexities are invoked, there is no general exact solution of the problem, and to make progress, one has to make various simplified and favourable assumptions. Since, one never knows beforehand which of such simplifications are valid, one cannot make any general claim as to whether continued GR collapse gives rise to BHs or Naked Singularities, or some other non-singular objects. As to the various claims about the occurrences of naked-singularities, we may recall [30].
“Although some theoretical counterexamples have been constructed, the general consensus is that these are all too artificial too occur naturally.”
In fact, same is true for all claims of BH formation in continued gravitational collapse too. In order to claim that, a spacetime singularity has been formed, it is not enough to find whether some light rays can escape outside before being trapped (on which claims of naked singularities are based). On the other hand, one must faithfully compute the comoving proper time all the way  to confirm that
to confirm that . Such a computation is possible only for the fictitious dust case, and for no physically realistic case. Thus all claims of formation of “naked singularities” are non-sound.
. Such a computation is possible only for the fictitious dust case, and for no physically realistic case. Thus all claims of formation of “naked singularities” are non-sound.
In fact by virtue of the general proof that trapped surfaces are actually not formed [31,32], it is most likely that continued collapse results in non-singular objects having external radius  [2,3]. The proof for non-occurrence of trapped surfaces was also offered by Kriele [33]. Ironically, such a non-occurrence of trapped surfaces and non-formation of finite mass BHs in continued collapse might be mistaken as evidence for formation of naked singularities. In the absence of a trapped surface or EH, such objects must keep on radiating and contracting even if at infinitesimally slow rate. In fact there are several GTR special solutions for physical gravitational collapse which suggest that effect of radiation pressure and dissipation may cause formation of hot radiating ultra-compact objects rather that any BH or naked singularity [34,35]. Radiation pressure apart, generation of tangential pressure too can arrest the continued collapse.
[2,3]. The proof for non-occurrence of trapped surfaces was also offered by Kriele [33]. Ironically, such a non-occurrence of trapped surfaces and non-formation of finite mass BHs in continued collapse might be mistaken as evidence for formation of naked singularities. In the absence of a trapped surface or EH, such objects must keep on radiating and contracting even if at infinitesimally slow rate. In fact there are several GTR special solutions for physical gravitational collapse which suggest that effect of radiation pressure and dissipation may cause formation of hot radiating ultra-compact objects rather that any BH or naked singularity [34,35]. Radiation pressure apart, generation of tangential pressure too can arrest the continued collapse.
As the contracting objects would keep on losing mass energy, it is likely that, they would approach the  true BH state. However, this state must not be allowed to be formed in finite commoving proper time, i.e., ever. This must be so because even for a
true BH state. However, this state must not be allowed to be formed in finite commoving proper time, i.e., ever. This must be so because even for a , BH, the timelike geodesic of an infalling material particle would tend to turn lightlike if the particle would ever arrive at the EH. Therefore, the most logical scenario seems to be one where continued gravitational collapse would indeed continue indefinitely (Eternally Collapsing Object: ECO) [22,23,31,32,36]. Since astrophysical plasma is always associated with imbedded magnetic field, ECO are expected to be ultra-magnetized with a pulsar like magnetosphere around. Thus it is quite likely the GR collapse results in the formation of Magnetospheric Eternally Collapsing Objects (MECOs).
, BH, the timelike geodesic of an infalling material particle would tend to turn lightlike if the particle would ever arrive at the EH. Therefore, the most logical scenario seems to be one where continued gravitational collapse would indeed continue indefinitely (Eternally Collapsing Object: ECO) [22,23,31,32,36]. Since astrophysical plasma is always associated with imbedded magnetic field, ECO are expected to be ultra-magnetized with a pulsar like magnetosphere around. Thus it is quite likely the GR collapse results in the formation of Magnetospheric Eternally Collapsing Objects (MECOs).
6. Conclusions
Even if one would prima-facie accept the BH paradigm which is based on the presumption that the integration constant appearing in the vacuum Schwarzschild solution 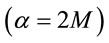 is finite for a massenpunkt or a “point mass” too, one lands up in many puzzles and unphysical happenings. For instance, one must wonder, if the EH is indeed a perfectly non-singular regular region, why would it require an infinite upward boost for an object to stay put there [6]. And such an infinite boost is required irrespective of whether one is using much maligned Schwarzschild coordinates or any other supposedly well behaved coordinates. Clearly, the requirement of an infinite boost and the property that nothing, not even light can escape the clutches of gravity at the EH are very much physical aspects, and they signify that the EH is a physical singularity. Yet, one overlooks such physical questions to defend the BH paradigm by inventing various other coordinate systems to somehow hide the physical problems associated with the EH. And here we considered the Kruskal coordinates which are believed to be the ultimate tool to establish the BH paradigm. As soon as the Kruskal extensions were proposed, they raised even more physical questions like the apparent existence of other universes, wormholes etc., and some authors pointed out some of the unphysical aspects. For instance Anderson & Gautreau [37] pointed out that the Kruskal scheme may involve causal violations even at
is finite for a massenpunkt or a “point mass” too, one lands up in many puzzles and unphysical happenings. For instance, one must wonder, if the EH is indeed a perfectly non-singular regular region, why would it require an infinite upward boost for an object to stay put there [6]. And such an infinite boost is required irrespective of whether one is using much maligned Schwarzschild coordinates or any other supposedly well behaved coordinates. Clearly, the requirement of an infinite boost and the property that nothing, not even light can escape the clutches of gravity at the EH are very much physical aspects, and they signify that the EH is a physical singularity. Yet, one overlooks such physical questions to defend the BH paradigm by inventing various other coordinate systems to somehow hide the physical problems associated with the EH. And here we considered the Kruskal coordinates which are believed to be the ultimate tool to establish the BH paradigm. As soon as the Kruskal extensions were proposed, they raised even more physical questions like the apparent existence of other universes, wormholes etc., and some authors pointed out some of the unphysical aspects. For instance Anderson & Gautreau [37] pointed out that the Kruskal scheme may involve causal violations even at . Belinfante hinted at some of the weird predictions of the Kruskal scheme [38]. Later Gautreau concluded that [39].
. Belinfante hinted at some of the weird predictions of the Kruskal scheme [38]. Later Gautreau concluded that [39].
“I give arguments showing that the reference system is not maximally extended, as is commonly reported in the literature. On both Novikov and Kruskal Szekeres spacetime diagrams, the left-hand side, corresponding to negative values of the spatial coordinate, should not be included when describing a physical spacetime. In turn, this means we have to rethink widely-accepted concepts such as black and white holes that arise from the usual picture of a maximally-extended Kruskal Szekeres spacetime”.
Antoci & Liebscher [40] pointed out that EH is actually a physical singularity and the weird picture of Kruskal coordinates is not realizable.
However what these authors have not pointed out is a much simpler and profoundly fundamental incongruity associated with the Kruskal coordinates. Note the original problem of the static central gravitational field, i.e., the Schwarzschild solution, is solved by using the natural assumption that the spacetime is asymptotically flat. Here, for , one must recover the Minkowski metric:
, one must recover the Minkowski metric:
 (53)
(53)
Very oddly, the Kruskal solution is NOT asymptotically flat.
As , the Kruskal metric becomes
, the Kruskal metric becomes
 (54)
(54)
One may recoincile this with the previous equation only by presuming  at
at 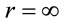 when in the original problem,
when in the original problem,  at
at . Thus Kruskal metric brazenly contradicts the foundations of the very problem it purported to solve. Actually, even in the limit,
. Thus Kruskal metric brazenly contradicts the foundations of the very problem it purported to solve. Actually, even in the limit,  , the skewed “Kruskal manifold is topologically different from the Minkowski manifold” [40].
, the skewed “Kruskal manifold is topologically different from the Minkowski manifold” [40].
As far as Differential Geometry and mathematics are concerned, one can indeed conceive of complex manifolds which cannot be covered by a single coordinate chart and may possess any number of strange properties. Such exercises could delight many mathematicians and keep them absorbed; but that does not mean that, the observable physical spacetime must be such complex, convoluted, strange and often self-contradictory. For instance, one may easily conceive of not ony 5-D but 26-D or any dimensional spacetime, and arrive at billions of exact solutions. Many such solutions could also suggest existence of even stranger kind of BHs, wormholes and what not. But such mathematical extravaganza need not have any relationship with the observable physical world.
Even for the innocuous 4-D GTR, most of the “exact solutions” could be physically misleading, and actually vacuous. For instance, it was recently found that, the innocuous simple problem of a strictly uniform density self-gravitating sphere is vacuous, because it actually corresponds to  [27]. Similarly, the exact solutions associated with the collapse of this homogeneous sphere too vacuous as they correspond to
[27]. Similarly, the exact solutions associated with the collapse of this homogeneous sphere too vacuous as they correspond to  [41]. And the collapse of a homogeneous pressure-less collapse (the OS collapse) too is vacuous because it corresponds to
[41]. And the collapse of a homogeneous pressure-less collapse (the OS collapse) too is vacuous because it corresponds to  [28,29]. As recently found, one of the most important metrics in GR, namely the de-Sitter metric, which is the basis for supposed “cosmic inflation” and “dark energy” is illusory because, for self-consistency, one must have cosmological constant
[28,29]. As recently found, one of the most important metrics in GR, namely the de-Sitter metric, which is the basis for supposed “cosmic inflation” and “dark energy” is illusory because, for self-consistency, one must have cosmological constant 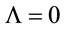 [42].
[42].
In GR, one is in principle free to use arbitrary coordinates; but the use of complex, convoluted coordinates invented by one mathematician after another need not lead to new physical realities. Similarly, while coordinate transformations could sometimes be mathematically convenient, they themselves must not lead to new physical realities. Accordingly, the very idea that the Kruskal coordinates are the most ideal coordinates and reveal various universes, white holes, worm holes etc. and which are not revealed by other coordinates are against the spirit of the principle of general covariance. Only if a specific coordinate can be associated with geometrically or physically relevant quantities, it may be considered as a better coordinate to represent the inherent physical reality despite the principle of covariance. And the Kruskal coordinates 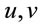 by no way could be related to any physical observables. As we just found, they even blatantly contradict the basic fact that the concerned spacetime is asymptotically flat. Note, the Kruskal coordinates
by no way could be related to any physical observables. As we just found, they even blatantly contradict the basic fact that the concerned spacetime is asymptotically flat. Note, the Kruskal coordinates  are constructed by using Schwarzschild/Hilbert coordinates
are constructed by using Schwarzschild/Hilbert coordinates . And if
. And if  are “bad” coordinates, how can the coordinates made out of them could be “good” coordinates?
are “bad” coordinates, how can the coordinates made out of them could be “good” coordinates?
We feel that the reason that the Kruskal coordinates give an infinite physical distortion is that they involve division by zero (see  and
and 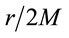 terms in Equations 2-3), because the mass of the point particle
terms in Equations 2-3), because the mass of the point particle 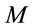 has been found to be zero. In contrast, the Schwarzschild radial coordinate
has been found to be zero. In contrast, the Schwarzschild radial coordinate  has direct geometrical significance because, by definition,
has direct geometrical significance because, by definition,  , represents the invariant area of 2-surfaces around the centre of symmetry. In view of such an invariant character,
, represents the invariant area of 2-surfaces around the centre of symmetry. In view of such an invariant character, 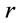 defines the luminosity distance too. Similarly, the Schwarzschild coordinate
defines the luminosity distance too. Similarly, the Schwarzschild coordinate 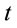 has a solid physical implication as the proper time measured by a distant inertial observer. Thus in reality, the Schwarzschild coordinates are the most appropriate coordinates for studying a problem having a spherical symmetry. (Note, this so-called “Schwarzschild coordinate”
has a solid physical implication as the proper time measured by a distant inertial observer. Thus in reality, the Schwarzschild coordinates are the most appropriate coordinates for studying a problem having a spherical symmetry. (Note, this so-called “Schwarzschild coordinate”  and the metric are originally due to Hilbert, and not due to Schwarzschild). On the other hand, these physically significant coordinates appear not to cover the interior region of a fictitious BH whose idea crops up when one one incorrectly presumes that even a neutral point particle has finite gravitational mass. In contrast, in Newtonian gravitation, a point particle may be assumed to have arbitrary mass. And as far as GR is concerned, there may not be any strictly point particle at all.
and the metric are originally due to Hilbert, and not due to Schwarzschild). On the other hand, these physically significant coordinates appear not to cover the interior region of a fictitious BH whose idea crops up when one one incorrectly presumes that even a neutral point particle has finite gravitational mass. In contrast, in Newtonian gravitation, a point particle may be assumed to have arbitrary mass. And as far as GR is concerned, there may not be any strictly point particle at all.
The great expectation that the Kruskal extension represents a new and complete physical picture was rightly dismissed by Dirac in 1962 [43]:
“The mathematicians can go beyond this Schwarzschild radius, and get inside, but I would maintain that this inside region is not physical space, because to send a signal inside and get it out again would take an infinite time, so I feel that the space inside the Schwarzschild radius must belong to a different universe and should not be taken into account in any physical theory.”
From a different consideration, Kiselev, Logunov, & Mestvirishvili too have shown that finite mass BHs are in contradiction with GTR [44]. Further long back Narlikar & Padmabhan too noted many conceptual difficulties associated with the concept of “Event Horizon” and “Black Hole” [45]:
“Nevertheless there are several conceptual difficulties associated with this simple and elegant solution that are usually ignored because of its manifest usefulness.”
“For the detection of any object by whatever means, it must come within the observer’s past lightcone. This does not ever happen for a BH. So none of the laws describing the behavior of BHs (as opposed to the Quasi BHs) are in principle detectable or testable by the class of observers who stay outside their event horizons. Since most observers (including those on the Earth) are of this type, to them the BH’s are not relevant as physical objects” [45].
“We therefore find that considering observers inside the event horizon makes the problems of interpretation even more difficult, and we wonder whether nature allows gravitational collapse to continue inside the event horizon at all” [45].
Indeed the SBH solution is exact and beautiful; and therefore, the resolution to all such paradoxes can be made only when we realize that while the integration constant  is indeed finite for an extended object, it shrinks to zero as the radius of the object shrinks to zero. In 1969, Bel noted that [46]:
is indeed finite for an extended object, it shrinks to zero as the radius of the object shrinks to zero. In 1969, Bel noted that [46]:
“Actually, several extensions have been proposed in the literature, the most commonly quoted being those of Finkelstein and Kruskal. Both extensions lead to spacetime models which are not globally static and are consequently inadequate for representing the exterior solution of a source in static equilibrium.”
Then by considering intrinsic differential geometry associated with the problem, Bel concluded that [46].
“Schwarzschild singularity becomes instead a real point singularity on which are localized the sources of the exterior static solution” (Emphasis by the author).
This means that the point particle is synomous with the Event Horizon, as has been repeatedly stressed by this author while being unaware about Bel’s ignored conclusion.
Of course, one obtains BH like solutions in many other gravity theories and all quantum gravity theories too. But everywhere it must be the same story; the BH solutions represent asymptotic static limits of dynamical solutions characterized by  and never realizable in physical world. Thus mathematical studies of BHs and questions like how such vacuum solutions can possess huge entropies and micro-states are only idle mathematical exercises without any physical content. In view of the asymptotic
and never realizable in physical world. Thus mathematical studies of BHs and questions like how such vacuum solutions can possess huge entropies and micro-states are only idle mathematical exercises without any physical content. In view of the asymptotic  BH solution, we realize that “point particles/ singularities” are never allowed by GTR even though the concept of such a “point particle” is required for mathematical tractability. Given this, the concept of elementary “strings” or “branes” seem to be important ones; such concepts, by definition, eliminate the point singularities. But ironically the super-string theories too take the appearances of static BH solutions seriously when the very concept of extended “strings” and “branes” are anti-thesis of singularities!
BH solution, we realize that “point particles/ singularities” are never allowed by GTR even though the concept of such a “point particle” is required for mathematical tractability. Given this, the concept of elementary “strings” or “branes” seem to be important ones; such concepts, by definition, eliminate the point singularities. But ironically the super-string theories too take the appearances of static BH solutions seriously when the very concept of extended “strings” and “branes” are anti-thesis of singularities!
Irrespective of the present study, there have been already direct proof that the integration constant appearing in the vaccuum Schwarzschild/Hilbert solution is zero [31,32,47,48]. Thus the massive compact BH candidates cannot be true BHs. Indeed there are significant amount of observational evidences, that the so-called BH candidates could be ultracompact, ultramagnetized, ultrahot balls of plasma [49-55]. Recall that the Sun too is a magnetized plasma and the violent eruptions like Coronal Mass Ejection (CME) could be traced to such magnetized plasma ativities. Similarly, much of the violent activities associated with the so-called BH candidates may be triggered by relativistic version of CMEs from the ultra-magnetized plasma of MECOs. Even if uncharged BHs would be assumed to be spinning, they are electromagnetically inert because no current can flow out of the central singularity, and no energy can be extracted [56]. On the other hand, spin down energy can be extracted from a spinning MECO as it would act like an ultra-relativistic pulsar [57].
Very recently, the Event Horizon Telescope has imaged a plasma jet coming out from a region within . Since it is bent by the gravitation of the central compact object [58], it is highly likely that this jet is emanating from the compact object rather than from its accretion disk. If so, this could be almost a direct confirmation that the central object here is a MECO rather than a true BH with an EH. Recall, solar prominences and coronal mass ejection from the Sun are plumes or bursts of plasma emerging from the magnetized plasma of the sun. Similarly, the plumes of plasma imaged from near the compact object of M87 is most likely the signature of a Magnetospheric ECO which is spewing out magnetized plasma irrespective of any accretion disk activity.
. Since it is bent by the gravitation of the central compact object [58], it is highly likely that this jet is emanating from the compact object rather than from its accretion disk. If so, this could be almost a direct confirmation that the central object here is a MECO rather than a true BH with an EH. Recall, solar prominences and coronal mass ejection from the Sun are plumes or bursts of plasma emerging from the magnetized plasma of the sun. Similarly, the plumes of plasma imaged from near the compact object of M87 is most likely the signature of a Magnetospheric ECO which is spewing out magnetized plasma irrespective of any accretion disk activity.
We note here that the faith in the non-existent “Event Horizon” and the pretention to be unaware about the relevant developments, have driven theoretical physics in a vicious blind alley. When Quantum Gravity is supposed to remove the BH singularity, it has actually been invoked to enhance the notion of BHs. On the one hand, physical reality of BHs are insisted by claiming that “the EH is a regular space-time in VACUUM, a mere coordinate singularity, with no physical effects”. On the other hand, the same EH is modeled sometimes as “membranes”, sometimes as “fluids”, sometimes as “Fuzzball”, sometimes as hard “brick walls”, and now as “Firewalls” [59] with most dazzling physical effects! And they never admit that they are running into such brazen contradictions because the very assumption of finite mass BHs is incorrect. As one can recall, these all started with endowing the avowed vacuum EH, a non-physical “coordinate singularity”, with magical thermodynamic properties and then inventing “Hawking Radiation” from there. In reality, even by mundane classical GTR, as we found here, there is no finite mass BH [28,31,32,47,48] there is no EH, no EH thermodynamics (except area A = 0, and entropy S = 0), no “Hawking Radiation”, and no voodoo “Firewall” [2,3,23,28,31,47]. Further instead of fictitious quantum gravitational “Hawking Radiation” or preHawking radiation, any gravitational collapse is accompanied by well understood radiation in the form of photons and neutrinos for which no unfounded QG is required [1-3,21-23,36].
Similarly, hypothetical magical effects associated with the claimed non-physical “coordinate singularity” have inspired formulation of mystic “Emergent Gravity” [60] and “Entropic Gravity” [61] speculations. One may of course imagine that the vacuum is meshed by elementary Planck scale cells; but that does not mean that such cells are moving randomly like the molecules of a real gas. Recall, as per the basic premises of Quantum Mechanics, if the Planck Length would tend to zero, one must recover classical results by which vacuum has zero entropy. But as per the “Emergent Gravity” formulation, the entropy of classical vacuum would be infinite (as Planck const à 0)! This shows complete unphysical and incorrect nature of such popular speculations. Atleast, Padmanabhan could have avoided such speculations by recalling his own honest conclusion:
“The discussion of physical behavior of black holes, classical or quantum, is only of academic interest” [45].
7. Endnote
A preprint by the same title (arXiv:astro-ph/9904162v1) has been there on Cornell Univ. Preprint ArXiv for the past 13 years. The fact that, this preprint has not received any criticism for 13 long years implies that its basic content is correct. The present version is a massive revision of the same preprint, it encompasses all the related developments that have taken place over 13 years; and practically, this is a highly updated new paper. It is nice to see that two anonymous referees of IJAA verified/ corrected all the relevant calculations.
8. Acknowledgements
The author thanks the anonymous referees for pointing out some errors/typos in the initial two versions of this manuscript. He also thanks IJAA for waiving the processing fee in view of the importance of this paper.