A Complete and Simple Solution to a Discrete-Time Finite-Capacity BMAP/D/c Queue ()
1. Introduction
The discrete-time multi-server queue with deterministic service times has gained importance in view of a number of potential practical applications to slotted digital telecommunication systems and other related areas (Bruneel and Wuyts [1]). It has been observed that arrival streams to these systems, in particular, tend to be correlated (see, e.g., Wittevrongel and Bruneel [2,3]). To model this correlated nature, a versatile point process called the discrete-time batch Markovian arrival process (D-BMAP) is introduced by Blondia and Casals [4] and widely used for analytical studies. This rich class of arrival processes contains a number of well-known arrival processes such as the Bernoulli process with independent identically distributed batch arrivals, the Markov modulated Bernoulli process, and a superposition of D-BMAP themselves (for more details, see Blondia and Casals [4]).
In this paper, we consider the D-BMAP/D/c/N queue, in which customers arrive according to D-BMAP and are served by one of c servers. The system capacity is 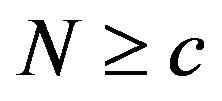 so that no more than N customers can be accommodated in the system at the same time. Customers who arrive to find the system full are assumed to depart the system immediately on arrivals. Specifically, we assume a partial acceptance model (Takagi [5], p. 367)
so that no more than N customers can be accommodated in the system at the same time. Customers who arrive to find the system full are assumed to depart the system immediately on arrivals. Specifically, we assume a partial acceptance model (Takagi [5], p. 367)
such that customers of an arriving batch are accepted until they fill all the available capacity, and the remaining customers, if any, are lost. Every accepted customer requires one slot for service that is assumed to start and end at slot boundaries.
For this queueing model, we present, based on an elementary Markov chain analysis, both steady-state and transient solutions to the system length (i.e., the number of customers in system) as well as to the system waiting time (i.e., the number of slots a customer spends in system) in a simple and unified manner. For similar discrete-time multi-server queueing models with infinite capacity, there have been some contributions by other authors: For a similar queue with infinite capacity (and correlated batch arrivals that belong to a subclass of B-DMAP arrivals), Sohraby and Zhang [6] analyze in transform domain the transient behavior of the system length and present an efficient numerical inversion method to calculate a few performance measures of interest. (They briefly discuss the finite capacity case as well.) For the D-BMAP/D/c queue, Alfa [7] assumes constant service times of multiple slots and presents an efficient algorithm making clever use of the structural property of the system to obtain the steady-state distributions of the system length and the system waiting time. Gao et al. [8] (Gao et al. [9]) assume constant service times of multiple slots (geometric service times) with a two-state Markovian arrival process to present a steady-state analysis of the system length and the system waiting time.
In this paper, we assume the finite-capacity model for the following three practical reasons. First and foremost, as demonstrated in this paper, the finite-capacity model of this paper is much simpler to analyze than its corresponding infinite-capacity counterpart (see Remark 1 below; also, see Sohraby and Zhang [6] for sophisticated analysis of the infinite-capacity model). Second, queueing models with finite capacity can serve as excellent approximations (by taking the system capacity N sufficiently large) for their corresponding infinite-capacity counterparts (see Remark 2 at the end of this paper). Third, all the queueing systems in reality have finite capacity.
We organize the paper as follows: In Section 2, we first present the steady-state system-length distribution based on the elementary Markov chain analysis. From this, important performance measures of practical interest are obtained, including the steady-state system waitingtime distribution. In addition, the corresponding transient solutions are presented in a simple and unified manner. In Section 3, we present a set of numerical results with various system capacities and a few different numbers of servers. For this, we use D-BMAP arrivals that characterize the superposition of certain video traffics. We end the paper with a remark on the finite-capacity model.
2. Analysis
In discrete-time queueing models, the time axis is divided into fixed-length intervals, called slots. It is assumed that customer arrivals and departures take place only at slot boundaries; thus, nothing is assumed to happen in the middle of a slot.
In the D-BMAP/D/c/N queue, customers arrive according to a D-BMAP with representation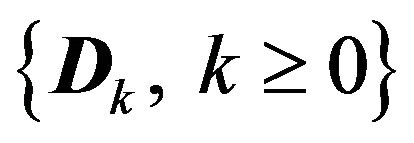 , where
, where 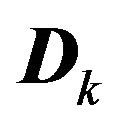 is an
is an 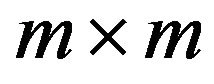 matrix with elements
matrix with elements
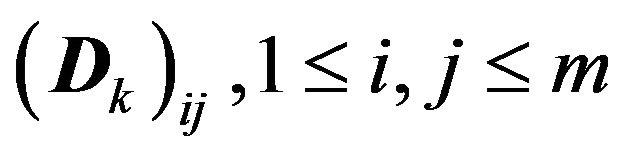 . This arrival process is governed by an m-state (or m-phase) underlying Markov chain (UMC). Specifically, let us suppose that the UMC is in some phase i in a certain slot. Then, with probabilities
. This arrival process is governed by an m-state (or m-phase) underlying Markov chain (UMC). Specifically, let us suppose that the UMC is in some phase i in a certain slot. Then, with probabilities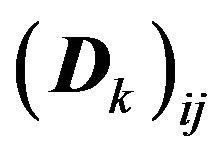 , there are
, there are 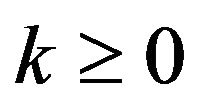 arrivals during the slot with the phase of the UMC being
arrivals during the slot with the phase of the UMC being  in the next slot. (See Blondia and Casals [4] for more details.) Note that the number of arrivals per slot (including those who are lost) is given by
in the next slot. (See Blondia and Casals [4] for more details.) Note that the number of arrivals per slot (including those who are lost) is given by
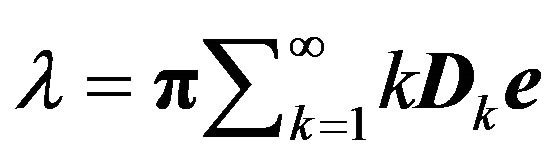 (1)
(1)
where  is the stationary probability vector of the UMC with the transition probability matrix (TPM)
is the stationary probability vector of the UMC with the transition probability matrix (TPM) 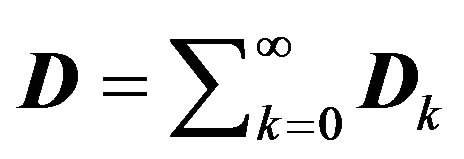 and
and 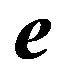 is a column vector of 1’s (note that
is a column vector of 1’s (note that  is obtained by solving simultaneously the equations
is obtained by solving simultaneously the equations 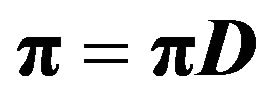 and
and 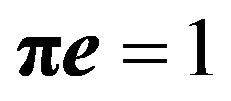 for
for ).
).
Now, we consider the discrete-time bivariate process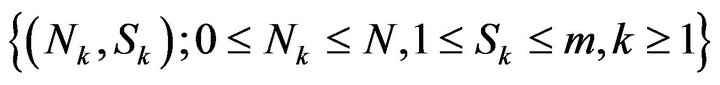 , where
, where  and
and  denote, respectively, the system length and the phase of the UMC just after the beginning of the kth slot. Then we consider the number of customers that arrive during the kth slot (denoted by
denote, respectively, the system length and the phase of the UMC just after the beginning of the kth slot. Then we consider the number of customers that arrive during the kth slot (denoted by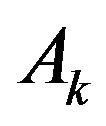 ) and the number of customers that depart at the end of the same slot (which is given by
) and the number of customers that depart at the end of the same slot (which is given by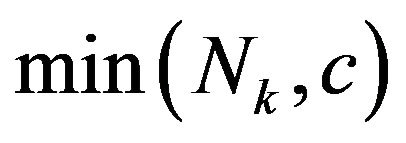 ); as a result, we have
); as a result, we have 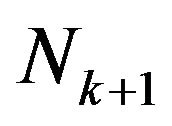 in terms of
in terms of 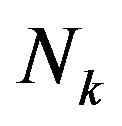 as follows:
as follows:
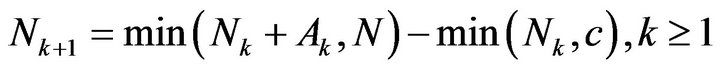 . (2)
. (2)
Note that 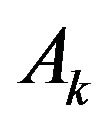 is dependent only on
is dependent only on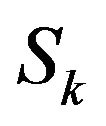 ; thus, we obtain the discrete-time Markov chain having the following TPM: (please see the formula below)
; thus, we obtain the discrete-time Markov chain having the following TPM: (please see the formula below)
where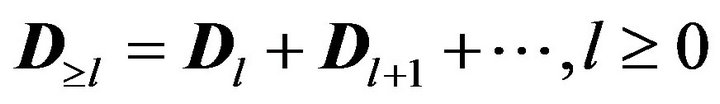 .
.
Let 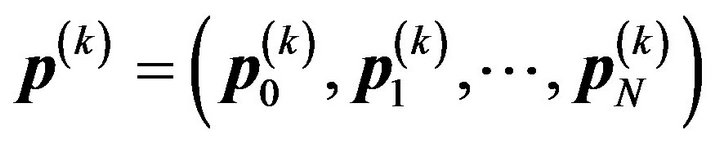 denote the state probability vector of the bivariate process just after the beginning of the kth slot, where
denote the state probability vector of the bivariate process just after the beginning of the kth slot, where 
and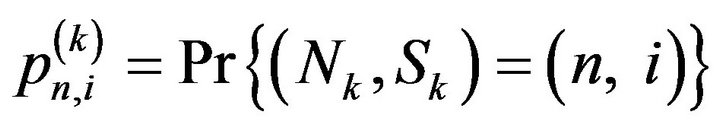 . Then it is immediate to have
. Then it is immediate to have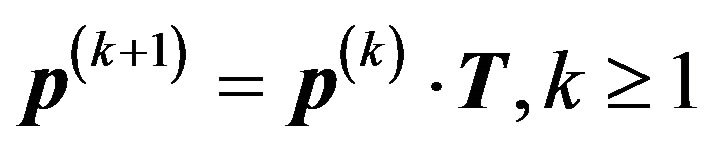 .
.
2.1. Steady-State Analysis
1) The System-Length Distribution: Let
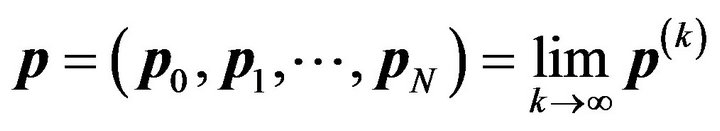 . Then the steady-state system-length distribution is obtained by solving simultaneously the equations
. Then the steady-state system-length distribution is obtained by solving simultaneously the equations 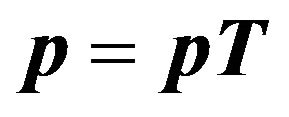 and
and 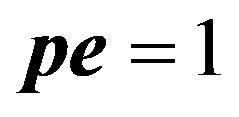 for
for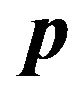 . This can be readily carried out by using mathematical software packages such as MATLAB, Mathematica, or even otherwise (see numerical examples in Section 3). Now, important performance measures of practical interest
. This can be readily carried out by using mathematical software packages such as MATLAB, Mathematica, or even otherwise (see numerical examples in Section 3). Now, important performance measures of practical interest
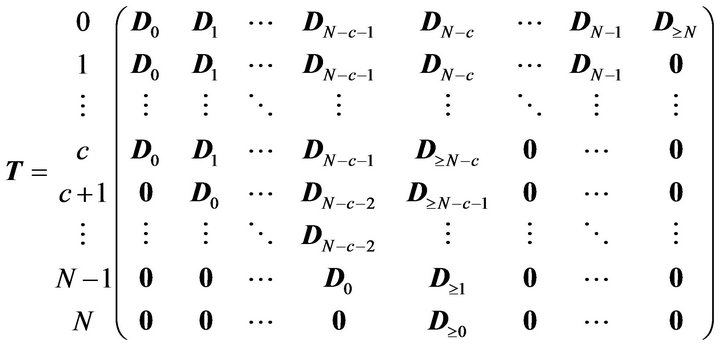 (3)
(3)
can be obtained from 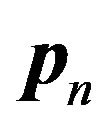 as given below.
as given below.
2) The Effective Arrival Rate and the Loss Probability: The number of arrivals (including those who are lost) per slot is given by
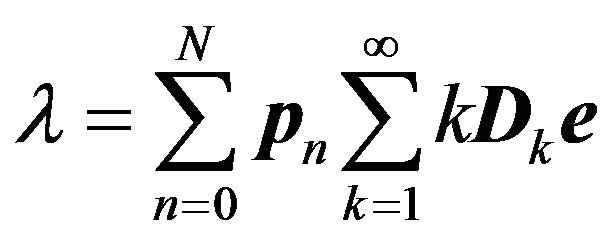 . (4)
. (4)
(Equation (4) reduces to (1) due to ). Under the assumption of partial acceptance, the number of accepted arrivals per slot (i.e., the effective arrival rate), on the other hand, is given by
). Under the assumption of partial acceptance, the number of accepted arrivals per slot (i.e., the effective arrival rate), on the other hand, is given by
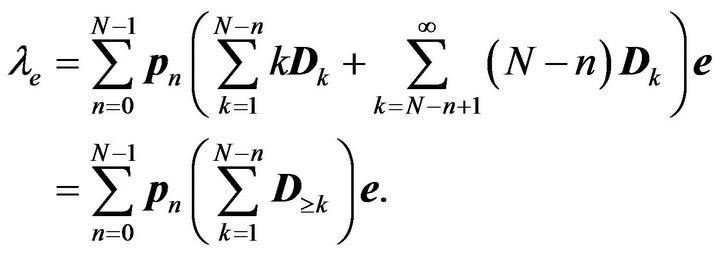 (5)
(5)
From (4) and (5), it is immediate to have the loss probability (i.e., the probability that a customer is lost) as follows:
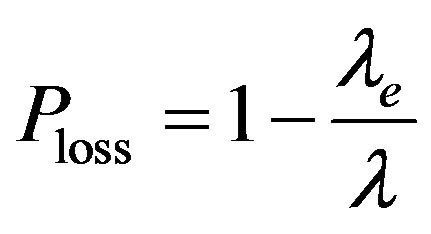 . (6)
. (6)
3) Moments of the System Length: Among others, the first moments of the numbers of customers in system and in service just after a slot boundary, denoted by  and
and 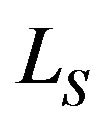 respectively, are given by
respectively, are given by
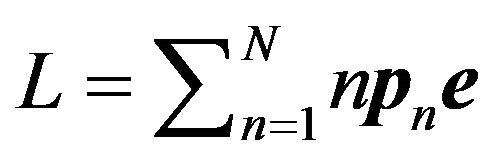 (7)
(7)
and
 . (8)
. (8)
Along the same lines, higher moments such as the variances of the numbers of customers in system and in service can be easily obtained.
Note that 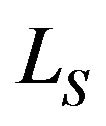 also represents the number of departures (by service completions) per slot, i.e., the departure rate, which, of course, should match with the effective arrival rate; that is,
also represents the number of departures (by service completions) per slot, i.e., the departure rate, which, of course, should match with the effective arrival rate; that is,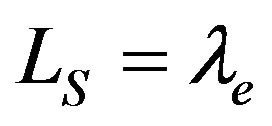 . Thus, the loss probability can be alternatively obtained from
. Thus, the loss probability can be alternatively obtained from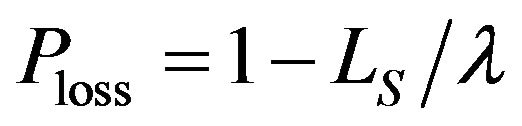 .
.
4) The System Waiting-Time Distribution of an Accepted Customer: Let 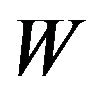 denote the system waiting time of an accepted customer, i.e., the number of slots an accepted customer spends in system (we do not count, as a part of the system waiting time, the slot in which she arrives). The probability that an accepted customer spends at most
denote the system waiting time of an accepted customer, i.e., the number of slots an accepted customer spends in system (we do not count, as a part of the system waiting time, the slot in which she arrives). The probability that an accepted customer spends at most 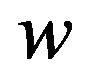 slots in system can be interpreted as the long-run fraction of such customers out of all accepted customers. That is,
slots in system can be interpreted as the long-run fraction of such customers out of all accepted customers. That is,
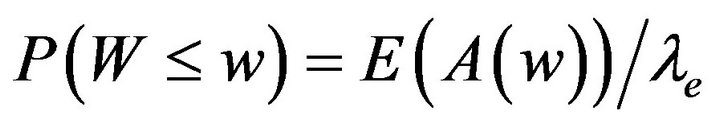 (9)
(9)
where 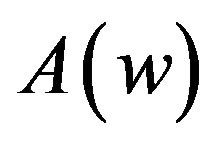 denotes the number of accepted customers per slot who are to spend at most
denotes the number of accepted customers per slot who are to spend at most 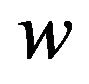 slots in system. Note that because the service times are single slot, one can foresee whether the system waiting time of an accepted customer will exceed
slots in system. Note that because the service times are single slot, one can foresee whether the system waiting time of an accepted customer will exceed 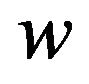 or not. Let
or not. Let  and
and  denote, respectively, the system length and the phase of the UMC just after the beginning of a slot at steady state. Then, conditioning on
denote, respectively, the system length and the phase of the UMC just after the beginning of a slot at steady state. Then, conditioning on 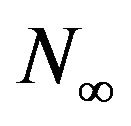 and
and , we have
, we have 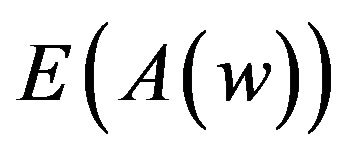 as follows;
as follows;
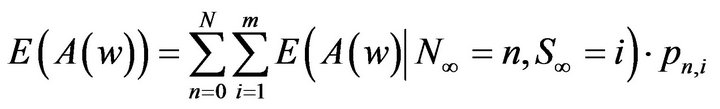 , (10)
, (10)
where
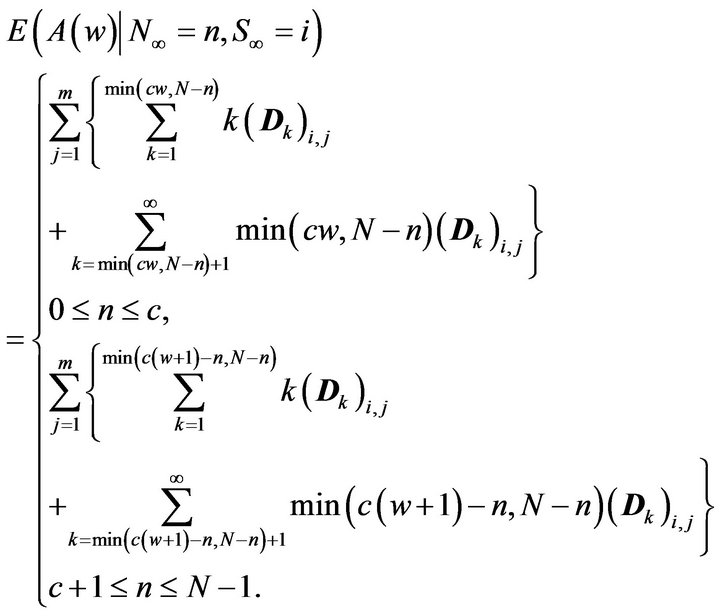
After simplifications (i.e., following the same procedure as used in getting the last term of (5)), we have
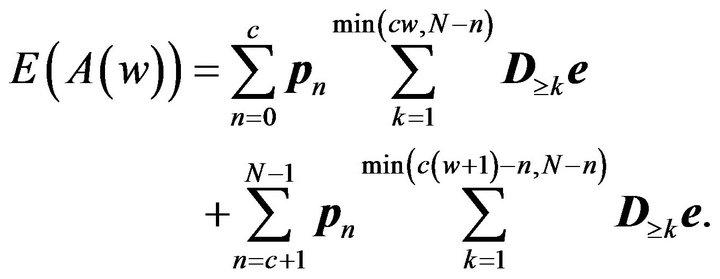 (11)
(11)
Substituting (11) into (9), we have the steady-state system waiting-time distribution of an accepted customer. From this, one can get performance measures of interest, such as the mean 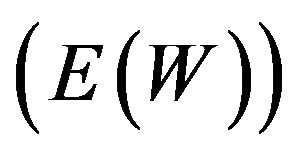 of the system waiting time and its tail probabilities. Also, one can get
of the system waiting time and its tail probabilities. Also, one can get 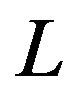 alternatively by Little’s formula,
alternatively by Little’s formula,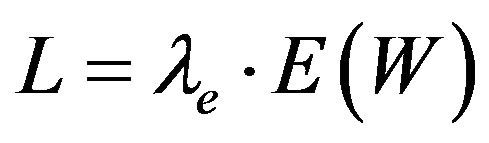 .
.
2.2. Transient Analysis
Note that  is obtained from
is obtained from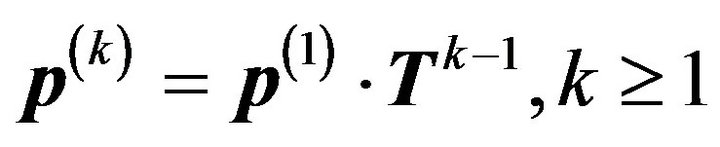 , where
, where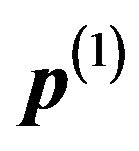 , the initial probability vector, is assumed to be given. Putting
, the initial probability vector, is assumed to be given. Putting 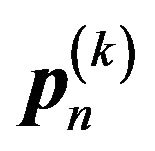 in place of
in place of 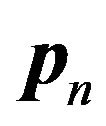 of (4) through (11) derived for the steady state, one can immediately obtain the corresponding transient results: the expected numbers of total, accepted, and lost arrivals during the
of (4) through (11) derived for the steady state, one can immediately obtain the corresponding transient results: the expected numbers of total, accepted, and lost arrivals during the  th slot, the moments of the numbers of customers in system as well as in service just after the beginning of the same slot, and the system waiting-time distribution of customers that are accepted during that slot.
th slot, the moments of the numbers of customers in system as well as in service just after the beginning of the same slot, and the system waiting-time distribution of customers that are accepted during that slot.
Remark 1: Transient analyses of queueing models are, in general, much more demanding than their stationary counterparts, because the formers need to take an additional variable (time) into consideration. See, e.g., Sohraby and Zhang [6] for a transient analysis of the queue of a similar kind with infinite capacity. This is not the case for the finite-capacity case, which can be analyzed in a remarkably simple and unified manner as presented in this paper.
3. Numerical Examples
For numerical work, we use the same D-BMAP arrival as the one given in Example 2 of Blondia and Casals [4]. In this example, they approximate the superposition of 3 video sources by the superposition of 30 independent identical on/off sources. The latter is then characterized by the D-BMAP, where the phase of the UMC corresponds to the number of active sources. (See Blondia and Casals [4] for the representation of this D-BMAP.)
For various system capacities 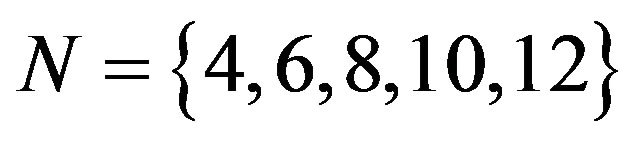 with different numbers of servers
with different numbers of servers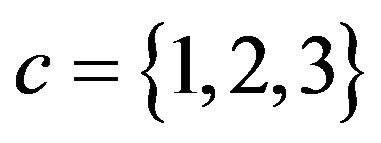 , Table 1 gives the steady-state loss probabilities. From this, one can see how fast the loss probability decreases as the system capacity N increases and as the number of servers c increases.
, Table 1 gives the steady-state loss probabilities. From this, one can see how fast the loss probability decreases as the system capacity N increases and as the number of servers c increases.
Table 2, with fixed capacity  and the numbers of servers
and the numbers of servers , gives the steady-state probabilities that the system waiting time of an accepted customer exceeds given threshold values
, gives the steady-state probabilities that the system waiting time of an accepted customer exceeds given threshold values . Such tail probabilities are one of the important performance measures of practical interest (particularly, in telecommunication area) that represent the quality of service.
. Such tail probabilities are one of the important performance measures of practical interest (particularly, in telecommunication area) that represent the quality of service.
For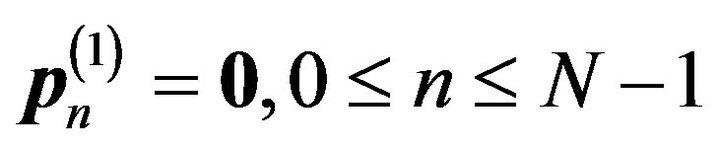 , and
, and
 (i.e., the system is initially full of customers) with fixed capacity
(i.e., the system is initially full of customers) with fixed capacity 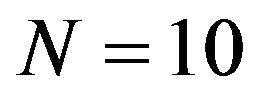 and the numbers of servers
and the numbers of servers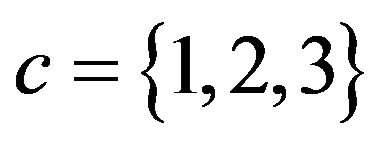 , Figure 1 displays how fast the expected system length of each system just after the beginning of the kth slot
, Figure 1 displays how fast the expected system length of each system just after the beginning of the kth slot  converges to its corresponding steadystate quantity. Other measures of practical interest can be obtained along the same lines.
converges to its corresponding steadystate quantity. Other measures of practical interest can be obtained along the same lines.
Remark 2: For each system with the number of ser- vers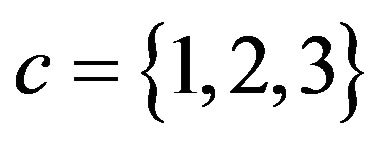 , we observe that the loss probability tends to converge to zero pretty quickly with a moderate increase in the system capacity (see Table 1); in addition, we observe that the tail probability of each waiting-time distribution decays pretty quickly as well (see Table 2). This seems to be mainly due to the extreme regularity of the (constant) service times and the multiple numbers of servers, both of which, individually as well as jointly, absorb burstiness of the arrival process considerably. Consequently, in such cases, one can effectively reduce the loss probability, the tail probability of waiting-time distribution, or both with a slight increase in the system capacity or the number of severs. Besides, in such cases as the loss probabilities are practically zero, a finite- capacity model can serve as an excellent approximation for the corresponding infinite-capacity counterpart. Then one can avoid sophisticated analyses for the infinite-
, we observe that the loss probability tends to converge to zero pretty quickly with a moderate increase in the system capacity (see Table 1); in addition, we observe that the tail probability of each waiting-time distribution decays pretty quickly as well (see Table 2). This seems to be mainly due to the extreme regularity of the (constant) service times and the multiple numbers of servers, both of which, individually as well as jointly, absorb burstiness of the arrival process considerably. Consequently, in such cases, one can effectively reduce the loss probability, the tail probability of waiting-time distribution, or both with a slight increase in the system capacity or the number of severs. Besides, in such cases as the loss probabilities are practically zero, a finite- capacity model can serve as an excellent approximation for the corresponding infinite-capacity counterpart. Then one can avoid sophisticated analyses for the infinite-
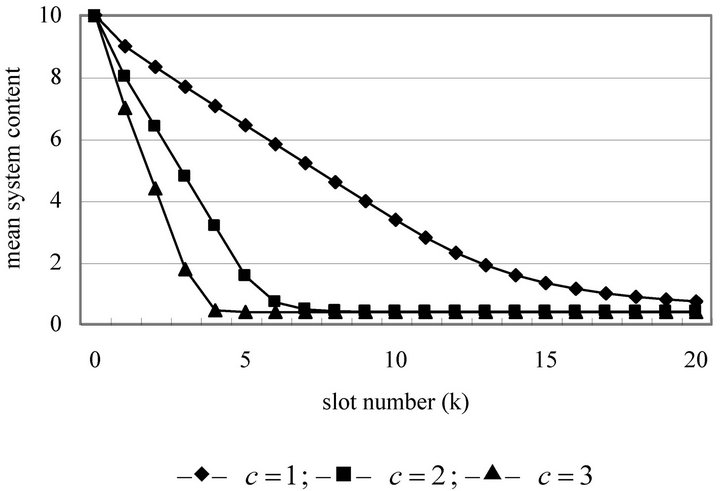
Figure 1. Transient mean system lengths.

Table 1. Steady-state loss probabilities.

Table 2. Steady-state tail probabilities of the system waiting time.
capacity model and get both steady-state and transient solutions in a remarkably simple and unified manner as presented in this paper.
We hope that the elementary Markov-chain based analysis we present in this paper for the finite-capacity D-BMAP/D/c/N queue would turn out to be beneficial to both theoreticians and practitioners who would like simple and straightforward practical solutions to their complex queueing systems.
4. Acknowledgements
The first author acknowledges with thanks the support provided by Prof. Sungjune Park and BISOM (Business Information Systems and Operations Management) of University of North Carolina at Charlotte, where he held an Adjunct-Visiting Professorship during his sabbatical year 2012 and where part of this work was done. The second author’s research was supported in part by grant 4010 NSERC RG.
NOTES