1. Introduction
Dielectric elastomer is a sub-category of Electroactive polymer. Dielectric elastomers are the materials with special mechanical and electrical performance, which can produced many kinds of mechanical responses with applied electric field [1-4]. Dielectric elastomers show large deformation (380%), high elastic energy density (3.4 J/g), high efficiency, high responsive speed, good reliability and durability. With these features dielectric elastomers have been intensely studied in these years due to their wide range application in different field’s for example medical, energy harvesting, soft robots, adaptive optics and electric generators [5]. In recent years, the stability analysis of dielectric elastomers is most popular issue, especially after Suo et al. proposed the electromechanical stability theory of dielectric elastomers [6-12]. In their research they discussed the case, when a layer of dielectric elastomer is sandwiched between two compliant electrodes and voltage applied between the electrodes then as the voltage ramps up, the layer thins down, so the same voltage produces a higher electric field which further thins down the elastomer as a positive feedback till the electrical breakdown of dielectric elastomer happen .It hinders the realization of large stable deformation. For removal of this instability, researchers used the prestretch conditions with material constants. With the positive feedback as a result of equation E = V/d where d is the thickness of dielectric elastomer, as the voltage increases then there is a possibility of mechanical breakdown of the elastomer at very high voltage after crossing the elastic limit.
In this paper, we discuss the mechanical stability of a dielectric elastomer under the influence of electric field. And we try to show that what will happen if we consider 
as stretch in case of elastomer [13-17].
In this work, we have adopted a new generalized set of strain variables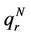 
to get the expression for second order elastic constant for a form deformed to orthorhombic structure [18-19]. The strength of a loaded system determined from the new moduli has been compared with the strength of Green and Stretch moduli.
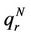is a generalised variable containing 
which show that when field is applied on dielectric elastomer then effect of it not only produced the deformation only in one direction but it will also affect the perpendicular positions. So 
is the tensor notation of the stretch 
which is used by researcher for explaining the electrical stability of dielectric elastomers. This concept of generalised co-ordinate is introduced for explaining the mechanical stability of bcc iron structure but here it is used for the dielectric elastomers.
2. Theoretical Approach
Consider a dielectric elastomer with three mechanical forces from three perpendicular directions and stretch λij.
Now we consider a new set of generalized geometric variable for a deformed structure
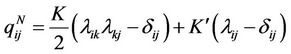
with
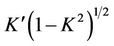(1)
where 
the Kroneckerdelta, K is can assume any suitable value and 
are the elements of stretch tensor.
The stretch variable defined by
(2)
where Xj and Xi are the reference and current rectangular co-ordinates of any lattice vector respectively.
The co-ordinates corresponding to new set of strain variables for an orthorhombic structure may explicitly be expressed by
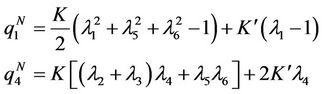(3)
where the tensor notation (ij) in Equation (1) are converted into matrix notation (r)
Depending upon K, the Equation (3) leads to a desired set of strain variables. For K = 0 and K = 1 the expression results to stretch and Green variables which are 
respectively.
The generalized set of elastic moduli Crs, can be defined by
(4)
where qr (r = 1, 2, 3,···, 6) are generalized co-ordinates. Using Equations (3) and (4), we obtain the expression for the set of new moduli 
i.e.
, 
, 
for example
(5)
Depending upon the value of K, Crs is capable of reproducing any desired set of elastic moduli.
And if Hessian (H)
is positive definite i.e. energy is minimum at equilibrium state. Then system must be stable.
3. Stability Condition
The difference between S-strength (corresponding to K = 0) and N-strength (corresponding to new defined variable) of a deformed crystal may be shown to be given by
(6)
(r, u, v = 1,2,···,6)
In this equation using Equation (3) we show that for cubic crystal deformed to orthorhombic structure
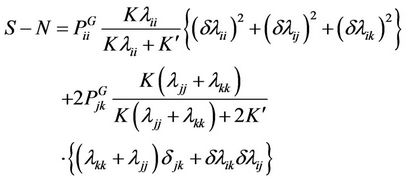(7)
Hill and Milestein calculated the values of S-G which can also be obtained from Equation (7) for K = 1
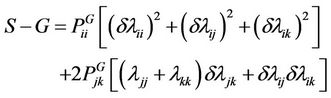(8)
From above equations, we obtain
(9)
Equations (7)-(9) enable the stability to be compared via the respective convexity criteria. A comparison of various strength for different loads and value of K' is given by Case 1: P1, P2, P3 ≥ 0; 
≥ 0: S ≥ N ≥ G Case 2: P1, P2, P3 ≥ 0; 
≤ 0: S ≥ G ≥ N Case 3: P1, P2, P3 ≤ 0; 
> 0: G ≥ S ≥ N Case 4: P1, P2, P3 ≤ 0; 
< 0: N ≥ G ≥ S In the above whole explanation E is the internal energy per unit reference cell and also function of generalised variable and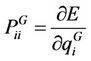
.
4. Conclusion & Discussion
The above whole explanation is based on the condition that the elastomer experience only the mechanical forces. But actuation in an elastomer consist effect of electric and mechanical field. So for explaining the mechanical stability it is considered that two mechanical forces are applied perpendicularly to each other and from third perpendicular direction electric field is applied to elastomer. The two mechanical forces behave as pre-stretch in elastomer. So P1 and P2 are equivalent to stresses produce in the elastomers due to these forces in their directions and P3 is the change in elastomer due to applied electric field in its direction. On basis of the above four conditions it is clear that the system becomes stable with theoretically explained generalised variable.